3.8: Practice Problems
- Page ID
- 207274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Problems for Section 3.1
Work on the following exercises on your own or with a partner.
- Draw a picture associated with the fraction \(\frac{1}{6}\).
- Draw a picture associated with the fraction \(\frac{3}{7}\). Is your picture really the amount of pie an individual would receive if three pies are shared among seven kids? Be very clear on this!
- Let’s work backwards! Here’s the answer to a division problem:
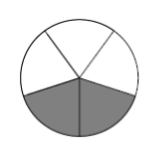
This represents the amount of pie an individual kid receives if some number of pies is shared among some number of children. How many pies? How many children? How can you justify your answers?
- Here’s another answer to a division problem:
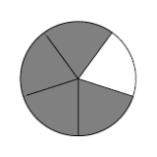
How many pies? How many children? How can you justify your answers?
- Here is another answer to a division problem:
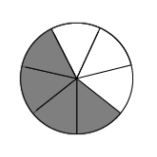
How many pies? How many children? How can you justify your answers?
- Leigh says that “\(\frac{3}{5}\) is three times as big as \(\frac{1}{5}\).” Is this right? Explain your answer.
- Draw a picture for the answer to the division problem \(\frac{4}{8}\). Describe what you notice about the answer.
- Draw a picture for the answer to the division problem \(\frac{2}{10}\). Describe what you notice about the answer.
- What does the division problem \(\frac{1}{1}\) represent? How much pie does an individual child receive?
- What does the division problem \(\frac{5}{1}\) represent? How much pie does an individual child receive?
- What does the division problem \(\frac{5}{5}\) represent? How much pie does an individual child receive?
- Here is the answer to another division problem. This is the amount of pie an individual child receives:

How many pies were in the division problem? How many kids were in the division problem? Justify your answers.
- Here is the answer to another division problem. This is the amount of pie an individual child receives:

How many pies were in the division problem? How many kids were in the division problem? Justify your answers.
- Many teachers have young students divide differently shaped pies into fractions. For example, a hexagonal pie is good for illustrating the fractions: \(\frac{1}{6}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}, \frac{5}{6},\; and\; \frac{6}{6} \ldotp\)
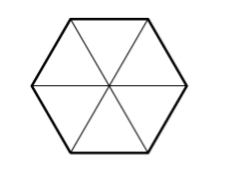
- Why is this shape used? What does \(\frac{1}{6}\) of a pie look like?
- What does \(\frac{6}{6}\) of a pie look like?
- What shape pie would be good for illustrating the fractions \(\frac{1}{8}\) up to \(\frac{8}{8}\)?
15. Some rectangular pies are distributed to some number of kids. This picture represents the amount of pie an individual child receives. The large rectangle represents one whole pie.

How many pies? How many kids? Carefully justify your answers!
Problems for Section 3.2
- Mix and Match: On the left, there are some fractions that have not been simplified. On the right are the simplified answers, in random order. Which simplified answer goes with which fraction? Notice that there are fewer answers than questions.
|
|
2. Use the Pies per Child Model to explain why the key fraction rule holds. That is, explain why each individual child gets the same amount of pie in these two situations:
- if you have \(a\) pies and \(b\) kids, or
- if you have \(xa\) pies and \(xb\) kids.
Problems for Section 3.3
Try these exercises on your own. For each addition exercise, also write down a Pies per Child interpretation of the problem. You might also want to draw a picture.
- What is \(\frac{1}{2} + \frac{1}{3}\)?
- What is \(\frac{2}{5} + \frac{37}{10}\)?
- What is \(\frac{1}{2} + \frac{3}{10}\)?
- What is \(\frac{2}{3} + \frac{5}{7}\)?
- What is \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}\)?
- What is \(\frac{3}{10} + \frac{4}{25} + \frac{7}{20} + \frac{3}{5} + \frac{49}{50}\)?
Now try these subtraction exercises.
- What is \(\frac{7}{10} - \frac{3}{10}\)?
- What is \(\frac{7}{10} - \frac{3}{20}\)?
- What is \(\frac{1}{3} - \frac{1}{5}\)?
- What is \(\frac{2}{35} - \frac{2}{7} + \frac{2}{5}\)?
- What is \(\frac{1}{2} - \frac{1}{4} - \frac{1}{8} - \frac{1}{16}\)?
Problems for Section 3.4
- Consider the following figure:

- If the shaded region represents \(4 \frac{3}{4}\), what is the whole?
- If the shaded region represents \(2 \frac{3}{8}\), what is the whole?
- If the shaded region represents \(\frac{19}{20}\), what is the whole?
- If the shaded region represents \(4 \frac{3}{4}\), what is the whole?
- Arrange each group of fractions in ascending order. Keep track of your thinking and your methods.
- \(\frac{3}{7}, \quad \frac{3}{4}, \quad \frac{3}{8} \ldotp \nonumber \)
- \(\frac{5}{6}, \quad \frac{7}{8}, \quad \frac{3}{4} \ldotp \nonumber \)
- \(\frac{8}{13}, \quad \frac{12}{17}, \quad \frac{1}{6} \ldotp \nonumber \)
- \(\frac{3}{7}, \quad \frac{3}{4}, \quad \frac{3}{8} \ldotp \nonumber \)
- Verify that the following are arithmetic sequences. Justify your answers.
- \(2, \quad 9, \quad 16, \quad 23, \quad 30, \quad 37, \quad 4, \quad 51, \ldots \nonumber \)
- \(\frac{1}{5}, \quad \frac{3}{5}, \quad 1, \quad \frac{7}{5}, \quad \frac{9}{5}, \quad \frac{11}{5}, \quad \frac{13}{5}, \quad 3, \ldots \nonumber \)
- \(1, \quad 2, \quad 4, \quad 8, \quad 16, \quad 32, \quad 64, \quad 128, \ldots \nonumber \)
- \(1, \quad 3, \quad 6, \quad 10, \quad 15, \quad 21, \quad 28, \quad 36, \ldots \nonumber \)
- \(\frac{2}{5}, \quad \frac{7}{10}, \quad 1, \quad \frac{13}{10}, \quad \frac{8}{5}, \quad \frac{19}{10}, \quad \frac{11}{5}, \quad \frac{5}{2}, \ldots \nonumber \)
- \(\frac{3}{5}, \quad \frac{6}{5}, \quad \frac{12}{5}, \quad \frac{24}{5}, \quad \frac{48}{5}, \quad \frac{96}{5}, \ldots \nonumber \)
- \(2, \quad 9, \quad 16, \quad 23, \quad 30, \quad 37, \quad 4, \quad 51, \ldots \nonumber \)
- Make up your own arithmetic sequence using whole numbers. Exchange sequences with a partner, and check if your partner’s sequence is really an arithmetic sequence.
- Consider: \[\frac{1}{4}, \quad \_\_\_\_, \quad \_\_\_\_, \quad \frac{1}{3} \nonumber \]
- Find two fractions between \(\frac{1}{4}\) and \(\frac{1}{3}\).
- Are the resulting four fractions in an arithmetic sequence? Justify your answer.
- Find two fractions between \(\frac{1}{4}\) and \(\frac{1}{3}\).
- Find two fractions between \(\frac{1}{6}\) and \(\frac{1}{5}\) so the resulting four numbers are in an arithmetic sequence. \[\frac{1}{6}, \quad \_\_\_, \quad \_\_\_\_, \quad \frac{1}{5} \nonumber \]
- Find two fractions between \(\frac{1}{6}\) and \(\frac{1}{5}\) so the resulting four numbers are in an arithmetic sequence.
\[\frac{1}{6}, \quad \_\_\_, \quad \_\_\_\_, \quad \frac{1}{5} \nonumber \]
Problems for Section 3.5
- Use an area model to compute each of the following products. Connect your answer to your representation.
- \(\dfrac{3}{4} \times \dfrac{5}{6}\)
- \(\dfrac{3}{8} \times \dfrac{4}{5}\)
- \(\dfrac{5}{8} \times \dfrac{3}{7}\)
- \(\dfrac{3}{4} \times \dfrac{5}{6}\)
- Use an area model to compute each of the following products. Connect your answer to your representation.
- \(\dfrac{2}{5} \cdot \dfrac{4}{3}\)
- \(\dfrac{3}{10} \cdot \dfrac{5}{4}\)
- \(\dfrac{5}{2} \cdot \dfrac{7}{4}\)
- \(\dfrac{2}{5} \cdot \dfrac{4}{3}\)
- Compute the following products, simplifying each of the answers as much as possible. You do not need to draw pictures, but you may certainly choose to do so if it helps.
- \(\dfrac{5}{11} \times \dfrac{7}{12}\)
- \(\dfrac{4}{7} \times \dfrac{4}{8}\)
- \(\dfrac{1}{2} \times \dfrac{1}{3}\)
- \(\dfrac{2}{1} \times \dfrac{3}{1}\)
- \(\dfrac{1}{5} \times \dfrac{5}{1}\)
- \(\dfrac{5}{11} \times \dfrac{7}{12}\)
- Explain how to find the products below by using three different methods (converting the whole number to a fraction with a denominator of one, Pies per Child Model, units and unitizing):
- \(4 \cdot \frac{3}{8}\)
- \(6 \cdot \frac{1}{5}\)
- \(4 \cdot \frac{3}{8}\)
- Compute the following products. Consider using the fraction rule, \(\dfrac{xa}{xb} = \dfrac{a}{b}\), to help you calculate.
- \(\dfrac{3}{4} \times \dfrac{1}{3}\)
- \(\dfrac{5}{5} \times \dfrac{7}{8}\)
- \(\dfrac{88}{88} \times \dfrac{541}{788}\)
- \(\dfrac{77876}{311} \times \dfrac{311}{77876}\)
- \(\dfrac{1}{2} \times \dfrac{2}{3} \times \dfrac{3}{4} \times \dfrac{4}{5} \times \dfrac{5}{6} \times \dfrac{6}{7} \times \dfrac{7}{8} \times \dfrac{8}{9} \times \dfrac{9}{10} \ldotp\)
- \(\dfrac{3}{4} \times \dfrac{1}{3}\)
- What do you think about Roy’s reasoning? Does it make sense? How would Roy explain the general rule for positive whole numbers
: \[\frac{xa}{xb} = \frac{a}{b} ? \nonumber \]
Roy says that the fraction rule
\[\frac{xa}{xb} = \frac{a}{b} \nonumber \]
is “obvious” if you think in terms of multiplying fractions. He reasons as follows:
We know multiplying anything by 1 does not change a number:
\[\begin{split} 1 \cdot 4 &= 4 \\ 1 \cdot 2014 &= 2014 \\ 1 \cdot \frac{5}{7} &= \frac{5}{7} \end{split} \nonumber \]
So, in general,
\[1 \cdot \frac{a}{b} = \frac{a}{b} \ldotp \nonumber \]
Now, \(\frac{2}{2} = 1\), so that means that
\[\frac{2}{2} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
which means
\[\frac{2a}{2b} = \frac{a}{b} \ldotp \nonumber \]
By the same reasoning, \(\frac{3}{3} = 1\), so that means that
\[\frac{3}{3} \cdot \frac{a}{b} = 1 \cdot \frac{a}{b} = \frac{a}{b}, \nonumber \]
which means
\[\frac{3a}{3b} = \frac{a}{b} \ldotp \nonumber \]
Problems for Section 3.6
- Determine the following quotients using the finding equal-sized groups approach.
- \(\dfrac{1}{3} \div \dfrac{1}{2}\)
- \(\dfrac{4}{9} \div \dfrac{1}{3}\)
- \(\dfrac{4}{5} \div \dfrac{1}{3}\)
- \(\dfrac{3}{5} \div \dfrac{3}{4}\)
- \(\dfrac{3}{2} \div \dfrac{1}{2}\)
- \(\dfrac{2}{3} \div \dfrac{1}{2}\)
- \(\dfrac{1}{3} \div \dfrac{1}{2}\)
- Use the common denominator method to find these quotients. If the fractions don't have common denominators, find their common denominator first.
- \(\dfrac{5}{8} \div \dfrac{3}{8}\)
- \(\dfrac{3}{8} \div \dfrac{5}{8}\)
- \(\dfrac{15}{33} \div \dfrac{1}{33}\)
- \(\dfrac{3}{4} \div \dfrac{8}{7}\)
- \(\dfrac{2}{3} \div \dfrac{1}{2}\)
- \(\dfrac{5}{8} \div \dfrac{1}{4}\)
- \(\dfrac{5}{8} \div \dfrac{3}{8}\)
- Rewrite the problems below as a missing factor multiplication question. Then find the quotient using what you know about multiplying fractions.
- \(\dfrac{6}{7} \div \dfrac{3}{7}\)
- \(\dfrac{10}{9} \div \dfrac{2}{3}\)
- \(\dfrac{25}{12} \div \dfrac{5}{6}\)
- \(\dfrac{6}{7} \div \dfrac{3}{7}\)
- Write each of the following in a simpler form using the Simplification Method.
- \(\dfrac{\frac{2}{3}}{\frac{1}{3}}\)
- \(\dfrac{2 \frac{1}{5}}{2 \frac{1}{4}}\)
- \(\dfrac{\frac{5}{7}}{\frac{3}{5}}\)
- \(\dfrac{\frac{3}{7}}{\frac{4}{5}}\)
- \(\dfrac{\frac{2}{3}}{\frac{1}{3}}\)
- Jessica calculated \(2 \dfrac{1}{5}\div 2 \dfrac{1}{4}\) in the following way: \(\dfrac{2 \frac{1}{5}}{2 \frac{1}{4}} = \dfrac{\frac{1}{5}}{\frac{1}{4}} = \dfrac{\frac{1}{5} \cdot 4}{\dfrac{1}{4} \cdot 4} = \dfrac{\frac{4}{5}}{1} = \frac{4}{5} \ldotp\) Is this solution correct, or is Jessica misunderstanding something? Carefully explain what is going on with this solution.
- Isaac calculated \(\dfrac{3}{7}\div\dfrac{4}{5}\) this way: \(\dfrac{\frac{3}{7}}{\frac{4}{5}} = \dfrac{\frac{3}{7} \cdot 7}{\frac{4}{5} \cdot 5} = \dfrac{3}{4} \ldotp\) Is this solution correct, or is Isaac misunderstanding something? Carefully explain what is going on with this solution.
- Compute each of the following, using the invert and multiply method.
- \(\frac{1}{2} \div \frac{1}{3}\)
- \(\frac{4}{5} \div \frac{3}{7}\)
- \(\frac{2}{3} \div \frac{1}{5}\)
- \(\frac{45}{59} \div \frac{902}{902}\)
- \(\frac{10}{13} \div \frac{2}{13}\)
- \(\frac{1}{2} \div \frac{1}{3}\)
Problems for Section 3.7
- Write five different division word problems that use whole numbers. Then change the problems so that they are fraction division problems instead. You might need to rewrite the problem a bit so that it makes sense.
- Solve the problems you created above. Provide your answer in the context of the problem.

