4.5: Growing Patterns
- Page ID
- 188089
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have seen many ways of developing algebraic thinking through different approaches, including the borders of a square problem, the use of the equal sign, and the balancing approach. In this section, we will continue exploring algebraic thinking by examining patterns in figures, as we did in the border-of-a-square applications. However, our focus in this section is on generalization through the consideration of cases and the logical explanation of this generalization.
Consider the following pattern made from square tiles.
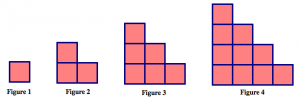
Discussion:
- Describe how you see this pattern growing. Be as specific as you can. Draw pictures and write an explanation to make your answer clear.
- Say as much as you can about this growing pattern. Can you draw pictures to extend the pattern?
- What mathematical questions can you ask about this pattern? Can you answer any of them?
You can think about the pattern of these figures by using different approaches. Consider the following rationales.
Solution 1: Think about columns. Each time the pattern adds a new column, it creates columns of size 1, 2, 3, 4, and so on.
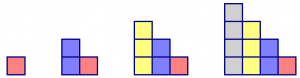
Solution 2: Think about rows. Each time the pattern adds a new row, it creates rows of size 1, 2, 3, 4, and so on.
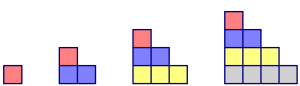
Solution 3: Think about diagonals. Each time the pattern adds a new diagonal, it creates diagonals of size 1, 2, 3, 4, and so on.
Discussion:
- How many tiles would you need to build the \(5^{th}\) figure in the pattern?
- How many tiles would you need to build the \(10^{th}\) figure in the pattern?
- How can you compute the number of tiles in any figure in the pattern? Consider, for example, the figure: \(n\), where \(n\) is any whole number.
Notice that the \(5^{th}\) figure will have an extra set of 5 tiles, so it will be a total of \(1+2+3+4+5\) tiles. We start to see a pattern. By drawing more figures, you will notice that the total of tiles in the \(10^{th}\) figure is: \(1+2+3+4+5+6+7+8+9+10\).
Consider the \(n^{th}\) figure, where \(n\) can be any whole number. Then we would expect that the number of tiles is the sum of all whole numbers from 1 to n. In other words, it will be: \(1+2+\cdots+(n-1)+n\). We can try this formula and find that for \(n=1\), we will have \(1\) tile, for \(n=2\), we will have \(1+2\) tiles, for \(n=3\), we will have \(1+2+3\) tiles, and so on. Using \(n\) supports the generalization of the pattern. This will allow us to calculate the number of tiles for the \(100^{th}\) figure, which will be \(1+2+3+4+5+\cdots+99+100\).
Discussion:
Consider the formula \(1+2+\cdots+(n-1)+n\). Is there another way of representing this in a simpler way? Use your creative thinking to solve this problem.
Notice that \(1 + 2 + 3 + \cdots + n = \dfrac{n(n+1)}{2}\), so the \(100^{th}\) figure, will have \(1+2+3+4+5+\cdots+99+100=\dfrac{100(100+1)}{2}=\dfrac{100(101)}{2}=5050\). How do we get the formula: \(\dfrac{n(n+1)}{2}\). Think of pairing the numbers from the ends.
We write the sum:
\[
1 + 2 + 3 + \cdots + (n-2) + (n-1) + n.
\]
Now pair the first and last terms:
\[
1 + n,
\]
the second and the second-to-last:
\[
2 + (n-1),
\]
the third and the third-to-last:
\[
3 + (n-2),
\]
and so on. Each pair adds up to the same value:
\[
1 + n = 2 + (n-1) = 3 + (n-2) = n + 1.
\]
There are \(\frac{n}{2}\) such pairs (or the idea still works if \(n\) is odd).
Therefore, the total sum is
\[
\text{Sum} = \frac{n}{2}(n+1) = \frac{n(n+1)}{2}.
\]
Discussion:
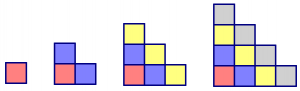
Explore the following approach and connect to the previous generalization.
Hy saw the pattern in a different way. Here’s what Hy drew:
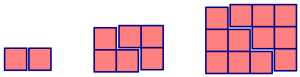
Hy's picture.
- Describe in words how Hy saw the pattern grow.
- How would Hy calculate the number of tiles needed to build the 10th figure in the pattern?
- How would Hy calculate the number of tiles needed to build the 100th figure in the pattern?
- How would Hy calculate the number of tiles needed to build any figure in the pattern?


