4.10: Practice Problems
- Page ID
- 203066
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Problems for Section 4.2
In the following exercises, simplify each expression.
- \(2^3−12÷(9−5)\)
- \(3^2−18÷(11−5)\)
- \(2+8(6+1)\)
- \(4+6(3+6)\)
- \(20÷4+6(5−1)\)
- \(33÷3+4(7−2)\)
- \(3(1+9⋅6)−4^2\)
- \(2[1+3(10−2)]\)
- \(5[2+4(3−2)]\)
- \(8+2[7−2(5−3)]−3^2\)
- \( (3x + 5) + (2x + 7) \)
- \( 4x^2 + x^2 + 6x + 3x \)
- \( 5x^2 + 3x + 9 + 2x^2 + 7x + 4 \)
- \( (6x + 8) - (2x - 5) + (x + 3) \)
- \( 3x^3 + 4x^2 + 7x + 9 + x^3 + 5x^2 + 2x + 1 \)
- \( (8x^2 - 3x + 6) + (4x^2 + 9x - 2) + (x - 1) \)
- \( 10x^3 + 6x^2 - x + 4 - (3x^3 - 2x^2 + 5x - 7) \)
- \( (7x^3 + 5x^2 - 4x + 1) + (2x^3 - x^2 + 9x - 6) + (x^2 - 3x + 4) \)
- \( 12x^4 - 3x^3 + 8x^2 - x + 5 + 4x^4 + x^3 - 6x^2 + 9x - 2 \)
- \( (5x^4 - 7x^3 + 12x^2 - 8x + 3) - (2x^4 + x^3 - 5x^2 + 6x - 9) + (x^4 - 3x^2 + 4) \)
- Why is it important to use the order of operations to simplify an expression?
Problems for Section 4.3
- The 25 case: Suppose that you have a large \(25 \times 25\) square with the unit squares along the border colored red. Adapt two of the techniques above to calculate the number of red unit squares. For each technique you used, write an explanation and include a picture. Think about how to use colors or other methods to make your picture and explanation clearer.
- Exploration: Suppose that you have 64 red squares. Can you use all of those squares to make the border of a larger square in a picture like the one above? If yes, what are the dimensions of the larger square? If not, why not?
- What if you have 30 red squares? Same questions.
- What if you have 256 red squares? Same questions.
- Generalization: If you have \(k\) red squares, is there a quick test you can do to decide if you can use all of those squares to make the border of a large square? Can you tell how big the square will be?
Problems for Section 4.4
- Examine the following equations. Decide: Is the statement always true, sometimes true, or never true? Justify your answers.
- \(\frac{a}{5} = \frac{5}{a} \)
- \(n + 3 = m \)
- \(3x = 2x + x \)
- \(5k = 5k + 1 \)
- Consider the equation\(20 + 3 = \_\_\_ \ldotp \nonumber \)
- Fill in the blank with something that makes the equation always true.
- Fill in the blank with something that makes the equation always false.
- Fill in the blank with something that makes the equation sometimes true and sometimes false.
- Consider the equation\(5 = 40-\_\_\_ \ldotp \nonumber \)
- Is it possible to fill in the blank with something that makes the equation always true? If yes, provide the answer. If not, explain why not.
- Is it possible to fill in the blank with something that makes the equation always false? If yes, provide the answer. If not, explain why not.
- Is it possible to fill in the blank with something that makes the equation sometimes true and sometimes false? If yes, provide the answer. If not, explain why not.
- Consider the equation\(x + 3 = \_\_\_ \ldotp \nonumber \)
- Is it possible to fill in the blank with something that makes the equation always true? If yes, provide the answer. If not, explain why not.
- Is it possible to fill in the blank with something that makes the equation always false? If yes, provide the answer. If not, explain why not.
- Is it possible to fill in the blank with something that makes the equation sometimes true and sometimes false? If yes, provide the answer. If not, explain why not.
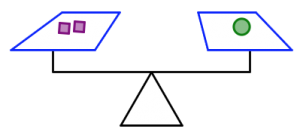
- Consider the given information in the first set of figures to determine the number of squares that will balance each scale in the second set of figures.
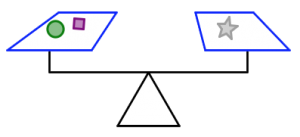
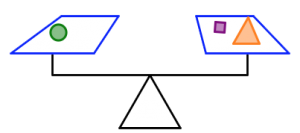
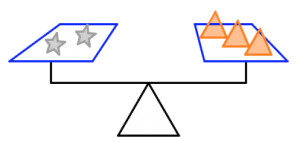
How many purple squares will balance the scale in each case? Justify your answers.
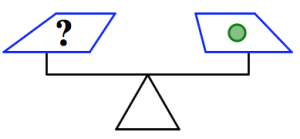
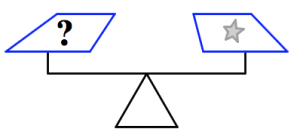
- In the pictures below, what will balance the last scale? Can you find more than one answer? Assume all figures that look the same also weigh the same, and the scale is balanced.
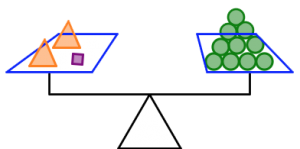
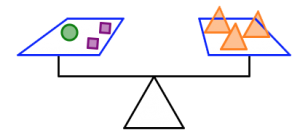
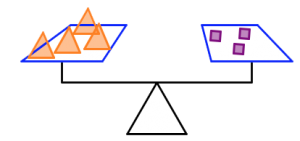
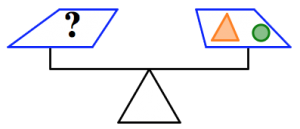
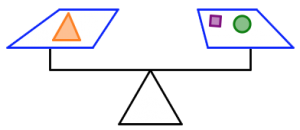
- Use the figure below to answer the questions. Assume all figures that look the same also weigh the same, and the scale is balanced.
- Which shape weighs the most: the square, the triangle, or the circle? Which shape weighs the least? Justify your answers.
- Which of the two scales is holding the most total weight? How do you know you’re right?
- Use a pan-balance representation, like the one provided in the figure below, to solve the equation \(5x+2=7\). Include a pan-balance representation to the left and annotate your representation with the corresponding equation to the right of the representation. Reflect on the importance of the equal sign when solving equations.
Problems for Section 4.5
1. The next patterns (A, B, C, D, E), do the following:
- Describe in words and pictures how you see the pattern growing.
- Calculate the number of tiles you would need to build the 10th figure in the pattern. Justify your answer based on how the pattern grows.
- Calculate the number of tiles you would need to build the 100th figure in the pattern.
- Describe how you can figure out the number of tiles in any figure in the pattern. Be sure to justify your answer based on how the pattern grows.
- Could you make one of the figures in the pattern using exactly 25 tiles? If yes, which figure? If no, why not? Justify your answer.
- Could you make one of the figures in the pattern using exactly 100 tiles? If yes, which figure? If no, why not? Justify your answer.
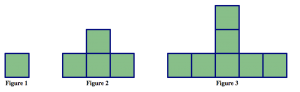
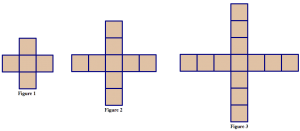
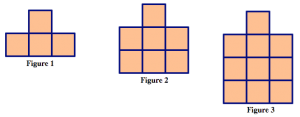Figure \(\PageIndex{1}\): Pattern E
Problems for Section 4.6
1. Use a pan-balance representation, like the one provided in the figure below, to solve each equation. Include a pan-balance representation to the left and annotate your representation with the corresponding equation to the right of the representation.
- x+3=10
- x+7=14
- 5x+2=7
- 3x+5=20
- 2x=10
- 4x=12
- 5x+1=3x+7
- x+5=3x+1
- 7x+7=6x+10
- 5x+8=3x+12
Problems for Section 4.7
For this section, please use the following links:
Practice Problems for linear equations: https://www.myopenmath.com/assess2/?cid=220955&aid=15606762#/
Practice Problems for linear equations with fractions and decimals: https://www.myopenmath.com/assess2/?cid=220955&aid=15607015#/
Use the following information in MyOpenMath for more practice.
Course ID: 220955
Course name: Elements of Mathematical Reasoning
Enrollment key: 103-niu
Problems for Section 4.8
1. The following work shows common mistakes students make when doing algebra. Find what the mistake is, explain it, and then solve the problem correctly.[1]
Problem 1: A student solved: \(x+6=\dfrac{4x}{3}\) by showing the following steps:
- \[x+6=\dfrac{4x}{3}\]
- \[x+6\times 3=\dfrac{4x}{3}\times 3\]
- \[x+18=4x\]
- \[x+18-x=4x-x\]
- \[18=3x\]
- \[\dfrac{18}{3}=\dfrac{3x}{3}\]
- \[x=6\]
Problem 2: A student solved: \(8x+7=2x\) by showing the following steps:
- \[8x+7=2x\]
- \[\dfrac{8x+7}{2}=\dfrac{2x}{2}\]
- \[4x+7=x\]
- \[4x+7-7=x-7\]
- \[4x=x-7\]
- \[4x-x=x-7-x\]
- \[3x=-7\]
- \[\dfrac{3x}{3}=\dfrac{-7}{3}\]
- \[x=-\dfrac{7}{3}\]
Problems for Section 4.9
1. What is additive growth, and how does it differ from multiplicative growth?
2. If you have a savings account that increases by $50 each month, how does this additive growth affect the total amount over time?
3. Imagine you receive $10 more each week as your allowance. How does the total amount you receive change each week compared to if it were a fixed amount?
4. How would the total amount in your savings account change if it increased by a fixed percentage each month instead of a fixed amount?
5. What is multiplicative growth, and how does it differ from additive growth?
6. If a population of bacteria doubles every hour, how does the population size change over time compared to additive growth?
7. Consider a situation where your investment grows by 5% each year. How does this multiplicative growth affect the total value of your investment compared to a fixed annual increase?
8. How does the total amount of money in an account grow if it compounds at a fixed interest rate versus increasing by a fixed amount?
9. Examine the following table. Determine whether the growth represented is linear, multiplicative, or neither. Provide a detailed explanation for your answer.
|
x |
0 |
1 |
2 |
3 |
4 |
|
y |
1 |
2 |
5 |
10 |
17 |
10. Draw a graph to represent both additive and multiplicative growth over time. How do the shapes of these graphs differ?
Selected Solutions for Section 4.2
- 5
- 6
- 58
- 58
- 29
- 31
- 149
- 50
- 30
- 5
- \( 5x + 12 \)
- \( 5x^2 + 9x \)
- \( 7x^2 + 10x + 13 \)
- \( 5x + 16 \)
- \( 4x^3 + 9x^2 + 9x + 10 \)
- \( 12x^2 + 7x + 3 \)
- \( 7x^3 + 8x^2 - 6x + 11 \)
- \( 10x^3 + 5x^2 + 2x - 1 \)
- \( 16x^4 - 2x^3 + 2x^2 + 8x + 3 \)
- \( 4x^4 - 8x^3 + 10x^2 - 14x + 16 \)