4.5: Set Operations with Two Sets

Last updated
Save as PDF

Page ID: 152045

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

A group of men and women of varying ages are smiling and posing for a group photo.

Figure 4.5.1: A large, multigenerational family contains an intersection and a union of sets. (credit: “Family Photo Shoot Bani Syakur” by Mainur Risyada/Flickr, CC BY 2.0)

Learning Objectives

After completing this section, you should be able to:

Determine the intersection of two sets.
Determine the union of two sets.
Determine the cardinality of the union of two sets.
Apply the concepts of AND and OR to set operations.
Draw conclusions from Venn diagrams with two sets.

The movie Yours, Mine, and Ours was originally released in 1968 and starred Lucille Ball and Henry Fonda. This movie, which is loosely based on a true story, is about the marriage of Helen, a widow with eight children, and Frank, a widower with ten children, who then have an additional child together. The movie is a comedy that plays on the interpersonal and organizational struggles of feeding, bathing, and clothing twenty people in one household.

If we consider the set of Helen's children and the set of Frank's children, then the child they had together is the intersection of these two sets, and the collection of all their children combined is the union of these two sets. In this section, we will explore the operations of union and intersection as it relates to two sets.

The Intersection of Two Sets

Intersection

The members that the two sets share in common are included in the intersection of two sets. To be in the intersection of two sets, an element must be in both the first set and the second set. In this way, the intersection of two sets is a logical AND statement. Symbolically, $A$ intersection $B$ is written as: $A \cap B$ . $A$ intersection $B$ is written in set builder notation as: $A \cap B = {x | x \in A and x \in B}$ .

Let us look at Helen's and Frank's children from the movie Yours, Mine, and Ours. Helen's children consist of the set $H = {Colleen, Nick, Janette, Tommy, Jean, Phillip, Gerald, Theresa, Joseph}$ and Frank's children are included in the set $F = {Mike, Rusty, Greg, Rosemary, Loise, Susan, Veronica, Mary, Germaine, Joan, Joseph}$ . $H$ intersection $F$ is the set of children they had together. $H \cap F = {Joseph}$ , because Joseph is in both set $H$ and set $F$ .

Example 4.5.1

Finding the Intersection of Set $A$ and Set $B$

Set $A = {1, 3, 5, 7, 9}$ and $B = {2, 3, 5, 7} .$ Find $A \cap B$

Answer: The intersection of sets $A$ and $B$ include the elements that set $A$ and $B$ have in common: 3, 5, and 7. $A \cap B = {3, 5, 7} .$

Your Turn 4.5.1

Set A = {h, a, p, y} and B = {s, a, d}. Find

A \cap B

Notice that if sets $A$ and $B$ are disjoint sets, then they do not share any elements in common, and < $A \cap B$ is the empty set, as shown in the Venn diagram below.

A two-set Venn diagram, A and B, not intersecting one another is given. Outside the diagram, it is labeled U.

Example 4.5.2

Determining the Intersection of Disjoint Sets

Set $A = {0, 2, 4, 6, 8}$ and set $B = {1, 3, 5, 7, 9} .$ Find $A \cap B .$

Answer: Because sets $A$ and $B$ are disjoint, they do not share any elements in common. So, the intersection of set $A$ and set $B$ is the empty set. $A \cap B = \emptyset .$

Your Turn 4.5.2

Set A = {red, yellow, blue} and Set B = {orange, green, purple}. Find

A \cap B

Notice that if set $A$ is a subset of set $B$ , then $A$ intersection $B$ is equal to set $A$ , as shown in the Venn diagram below.

A two-set Venn diagram, A and B, where A is inside B is depicted. Outside the diagram, it is labeled U.

Example 4.5.3

Finding the Intersection of a Set and a Subset

Set $A = {1, 3, 5, \dots}$ and set $B = ℕ = {1, 2, 3, \dots}$ Find $A \cap B .$

Answer: Because set $A$ is a subset of set $B$ , $A$ intersection $B$ is equal to set $A$ . $A \cap B = A = {1, 3, 5, \dots},$ the set of odd natural numbers.

Your Turn 4.5.3

Set A = {a, b, c, ..., z} and set B = {a, e, i, o, u}. Find

A \cap B

The Union of Two Sets

Like the union of two families in marriage, the union of two sets includes all the members of the first set and all the members of the second set.

Union

To be in the union of two sets, an element must be in the first set, the second set, or both. In this way, the union of two sets is a logical inclusive OR statement. Symbolically, $A$ union $B$ is written as: $A \cup B .$ $A$ union $B$ is written in set builder notation as: $A \cup B = {x | x \in A or x \in B} .$

Let us consider the sets of Helen's and Frank's children from the movie Yours, Mine, and Ours again. Helen's children is set $H = {Colleen, Nick, Janette, Tommy, Jean, Phillip, Gerald, Theresa, Joseph}$ and Frank's children is set $F = {Mike, Rusty, Greg, Rosemary, Loise, Susan, Veronica, Mary, Germaine, Joan, Joseph}$ . The union of these two sets is the collection of all nineteen of their children, $H \cup F = {Colleen, Nick, Janette, Tommy, Jean, Phillip, Gerald, Theresa, Joseph, Mike, Rusty, Greg, Rosemary, Loise, Susan, Veronica, Mary, Germaine, Joan} .$
Notice, Joseph is in both set $H$ and set $F$ , but he is only one child, so, he is only listed once in the union.

Example 4.5.4

Finding the Union of Sets $A$ and $B$ When $A$ and $B$ Overlap

Set $A = {1, 3, 5, 7, 9}$ and set $B = {2, 3, 5, 7}$ . Find $A \cup B$ .

Answer: $A$ union $B$ is the set formed by including all the unique elements in set $A$ , set $B$ , or both sets $A$ and $B$ : $A \cup B = {1, 3, 5, 7, 9, 2} .$ The first five elements of the union are the five unique elements in set $A$ . Even though 3, 5, and 7 are also members of set $B$ , these elements are only listed one time. Lastly, set $B$ includes the unique element 2, so 2 is also included as part of the union of sets $A$ and $B$ .

Your Turn 4.5.4

Set A = {h, a, p, y} ad set B = {s, a, d}. Find

A \cup B.

When observing the union of sets $A$ and $B$ , notice that both set $A$ and set $B$ are subsets of $A \cup B$ . Graphically, $A \cup B$ can be represented in several different ways depending on the members that they have in common. If $A$ and $B$ are disjoint sets, then $A \cup B$ would be represented with two disjoint circles within the universal set, as shown in the Venn diagram below.

If sets $A$ and $B$ share some, but not all, members in common, then the Venn diagram is drawn as two separate circles that overlap.

A two-set Venn diagram, A and B, intersecting one another is given. Outside the diagram, it is labeled U.

If every member of set $A$ is also a member of set $B$ , then $A$ is a subset of set $B$ , and $A \cup B$ would be equal to set $B$ . To draw the Venn diagram, the circle representing set $A$ should be completely enclosed in the circle containing set $B$ .

Example 4.5.5

Finding the Union of Sets $A$ and $B$ When $A$ and $B$ Are Disjoint

Set $A = {0, 2, 4, 6, 8}$ and set $B = {1, 3, 5, 7, 9} .$ Find $A \cup B .$

Answer: Because sets $A$ and $B$ are disjoint, the union is simply the set containing all the elements in both set $A$ and set $B$ . $A \cup B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} .$

Your Turn 4.5.5

Set A = {red, yellow, blue} and Set B = {orange, green, purple}. Find

A \cup B

Example 4.5.6

Finding the Union of Sets $A$ and $B$ When One Set is a Subset of the Other

Set $A = {1, 3, 5, \dots}$ and set $B = ℕ = {1, 2, 3, \dots} .$ Find $A \cup B .$

Answer: Because set $A$ is a subset of set $B$ , $A$ union $B$ is equal to set $B$ . $A \cup B = ℕ = {1, 2, 3, \dots} = B .$

Your Turn 4.5.6

Set A = {a, b, c, ..., z} and set B = {a, e, i, o, u}. Find

A \cup B

Video

The Basics of Intersection of Sets, Union of Sets and Venn Diagrams

Let's think back to our example of the children from the movie Yours, Mine, and Ours. We had $n (H) =9$ , since Helen had 9 children. We had $n (F) =11$ , since Frank had 11 children. What was $n (H \cup F)$ ? You may be tempted to guess that it was $9 + 11 = 20$ . But $n (H \cup F)$ was actually 19. Remember that the child Helen and Frank had together (Joseph) is included in set $H$ and set $F$ , but he should only be counted once in $H \cup F$ . We generalize this result in the formula below.

Cardinality of the Union of Two Sets

For any sets A and B, $n (A \cup B) = n (A) + n (B) - n (A \cap B)$

Example 4.5.7

Determining the Cardinality of the Union of Two Sets

The number of elements in set $A$ is 10, the number of elements in set $B$ is 20, and the number of elements in $A$ intersection $B$ is 4. Find the number of elements in $A \cup B$ .

Answer: Using the formula for determining the cardinality of the union of two sets, we can say $n (A \cup B) = n (A) + n (B) - n (A \cap B) = 10 + 20 - 4 = 26.$

Your Turn 4.5.7

If n(A) = 23, n(B) = 17, and n(

A \cap B

)=7. Find n(

A \cup B

Example 4.5.8

Determining the Cardinality of the Union of Two Disjoint Sets

If $A$ and $B$ are disjoint sets and the cardinality of set $A$ is 37 and the cardinality of set $B$ is 43, find the cardinality of $A \cup B$ .

Answer: To find the cardinality of $A$ union $B$ , apply the formula, $n (A \cup B) = n (A) + n (B) - n (A \cap B) .$ Because sets $A$ and $B$ are disjoint, $A \cap B$ is the empty set, therefore $n (A \cap B) = n (\emptyset) = 0$ and $n (A \cup B) = 37 + 43 - 0 = 80.$

Your Turn 4.5.8

A \cap B = \emptyset

, n(A) = 35, and n(B) = 78, then find

n (A \cup B)

Applying Concepts of “AND” and “OR” to Set Operations

To become a licensed driver, you must pass some form of written test and a road test, along with several other requirements depending on your age. To keep this example simple, let us focus on the road test and the written test. If you pass the written test but fail the road test, you will not receive your license. If you fail the written test, you will not be allowed to take the road test and you will not receive a license to drive. To receive a driver's license, you must pass the written test AND the road test. For an “AND” statement to be true, both conditions that make up the statement must be true. Similarly, the intersection of two sets $A$ and $B$ is the set of elements that are in both set $A$ and set $B$ . To be a member of $A \cap B$ , an element must be in set $A$ and also must be in set $B$ . The intersection of two sets corresponds to a logical "AND" statement.

The union of two sets is a logical inclusive "OR" statement. Say you are at a birthday party and the host offers Leah, Lenny, Maya, and you some cake or ice cream for dessert. Leah asks for cake, Lenny accepts both cake and ice cream, Maya turns down both, and you choose only ice cream. Leah, Lenny, and you are all having dessert. The “OR” statement is true if at least one of the components is true. Maya is the only one who did not have cake or ice cream; therefore, she did not have dessert and the “OR” statement is false. To be in the union of two sets $A$ and $B$ , an element must be in set $A$ or set $B$ or both set $A$ and set $B$ .

Example 4.5.9

Applying the "AND" or "OR" Operation

$A = {0, 3, 6, 9, 12}, B = {0, 4, 8, 12, 16},$ and $C = {1, 2, 3, 5, 8, 13} .$

Find the set consisting of elements in:

$A and B .$
$A or B .$
$A or C .$
$(B and C) or A .$

Answer

$A and B = A \cap B = {0, 12},$ because only the elements 0 and 12 are members of both set $A$ and set $B$ .
$A or B = A \cup B = {0, 3, 4, 6, 8, 9, 12, 16},$ because the set $A$ or $B$ is the collection of all elements in set $A$ or set $B$ , or both.
$A or C = A \cup C = {0, 1, 2, 3, 5, 6, 8, 9, 12, 13},$ because the set $A$ or $C$ is the collection of all elements in set $A$ or set $C$ , or both.
$(B and C) or A = (B \cap C) \cup A .$ Parentheses are evaluated first: $(B and C) = B \cap C = {8},$ because the only member that both set $B$ and set $C$ share in common is 8. So, now we need to find ${8} or {0, 3, 6, 9, 12},$ Because the word translates to the union operation, the problem becomes ${8} \cup {0, 3, 6, 9, 12},$ which is equal to ${0, 3, 6, 8, 9, 12} .$

Your Turn 4.5.9

Set A = {h, a, p, y}, set B = {a, w, e, s, o, m}, and set C = {m, a, t, h}.
Find the set consisting of elements in:

1. A or B

2. A and C

3. B or C

4. (A and C) and B

Example 4.5.10

Determine and Apply the Appropriate Set Operations to Solve the Problem

Don Woods is serving cake and ice cream at his Juneteenth celebration. The party has a total of 54 guests in attendance. Suppose 30 guests requested cake, 20 guests asked for ice cream, and 12 guests did not have either cake or ice cream.

How many guests had cake or ice cream?
How many guests had cake and ice cream?

Answer

The total number of people at the party is 54, and 12 people did not have cake or ice cream. Recall that the total number of elements in the universal set is always equal to the number of elements in a subset plus the number of elements in the complement of the set, $n (U) = n (A) + n (A^{'}) .$ That means $54 = n (cake or ice cream) + n (not (cake or ice cream))$ , or equivalently, $n (cake \cup ice cream) = 54 - n ({(cake \cup ice cream)}^{'}) = 54 - 12 = 42.$ A total of 42 people at the party had cake or ice cream.
To determine the number of people who had both cake and ice cream, we need to find the intersection of the set of people who had cake and the set of people who had ice cream. From Question 1, the number of people who had cake or ice cream is 42. This is the union of the two sets. The formula for the union of two sets is $n (A \cup B) = n (A) + n (B) - n (A \cap B) .$ Use the information given in the problem and substitute the known values into the formula to solve for the number of people in the intersection: $42 = 30 + 20 - n (A \cap B) .$ Adding 30 and 20, the equation simplifies to $42 = 50 - n (cake and ice cream) .$ Which means $n (cake and ice cream) = 50 - 42 = 8.$

Your Turn 4.5.10

Ravi and Priya are serving soup and salad along with the main course at their wedding reception. The reception will have a total of 150 guests in attendance. A total of 92 soups and 85 salads were ordered, while 23 guests did not order any soup or salad.

1.How many guests had soup or salad or both?

2.How many guests had both soup and a salad?

Who Knew?

The Real Inventor of the Venn Diagram

John Venn, in his writings, references works by both John Boole and Augustus De Morgan, who referred to the circle diagrams commonly used to present logical relationships as Euler's circles. Leonhard Euler's works were published over 100 years prior to Venn's, and Euler may have been influenced by the works of Gottfried Leibniz.

So, why does John Venn get all the credit for these graphical depictions? Venn was the first to formalize the use of these diagrams in his book Symbolic Logic, published in 1881. Further, he made significant improvements in their design, including shading to highlight the region of interest. The mathematician C.L. Dodgson, also known as Lewis Carroll, built upon Venn’s work by adding an enclosing universal set.

Invention is not necessarily coming up with an initial idea. It is about seeing the potential of an idea and applying it to a new situation.

References:

Margaret E. Baron. "A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn." The Mathematical Gazette, vol. 53, no. 384, 1969, pp. 113-125. JSTOR, www.jstor.org/stable/3614533. Accessed 15 July 2021.

Deborah Bennett. "Drawing Logical Conclusions." Math Horizons, vol. 22, no. 3, 2015, pp. 12-15. JSTOR, www.jstor.org/stable/10.4169/mathhorizons.22.3.12. Accessed 15 July 2021.

Drawing Conclusions from a Venn Diagram with Two Sets

All Venn diagrams will display the relationships between the sets, such as subset, intersecting, and/or disjoint. In addition to displaying the relationship between the two sets, there are two main additional details that Venn diagrams can include: the individual members of the sets or the cardinality of each disjoint subset of the universal set.

A Venn diagram with two subsets will partition the universal set into 3 or 4 sections depending on whether they are disjoint or intersecting sets. Recall that the complement of set $A$ , written $A^{'},$ is the set of all elements in the universal set that are not in set $A .$

A two-set disjoint Venn diagram and a two-set intersecting Venn diagram are depicted side by side. Outside both the Venn diagrams U is marked at the top left corner. The two sets of both the Venn diagrams are labeled A and B. In the first Venn diagram, Outside the set, the complement of A union B is given. In the second Venn diagram, Set A shows A union of B complement. Set B shows B union of A complement. The intersection of the sets shows A union B. Outside the set, the complement of A union B is given.

Example 4.5.11

Using a Venn Diagram to Draw Conclusions about Set Membership

A two-set Venn diagram not intersecting one another is given. The first set is labeled A while the second set is labeled B. Set A shows 1, 3, 5, 7. Set B shows 2, 4, 8, 6. Outside the sets, 0, 9 are given. Outside the Venn diagram, it is marked 'U equals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).'

Find $A \cup B .$
Find $A \cap B .$
Find $B^{'}$ .
Find $n (B^{'}) .$

Answer

$A \cup B = {1, 2, 3, 4, 5, 6, 7, 8},$ because $A \cup B$ is the collection of all elements in set $A$ or set $B$ or both.
Because $A$ and $B$ are disjoint sets, there are no elements that are in both $A$ and $B$ . Therefore, $A \cap B$ is the empty set, $A \cap B = \emptyset .$
The complement of set $B$ is the set of all elements in the universal set that are not in set $B$ : $B^{'} = {0, 1, 3, 5, 7, 9} .$
The cardinality, or number of elements in set $B^{'}, is n (B^{'}) = 6.$

Your Turn 4.5.11

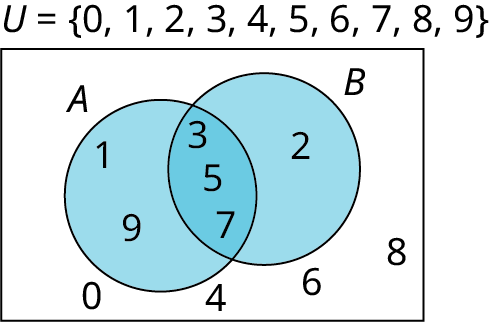
A two-set Venn diagram intersecting one another is given. The first set is labeled A while the second set is labeled B. Set A shows 1, 9. Set B shows 2. The intersection of the sets shows 3, 5, 7. Outside the sets, 0, 4, 6 are given. Outside the Venn diagram, it is marked 'U equals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).'

Find $A \cap B$
Find $A \cup B$
Find $A \cap B'$
Find $n (A \cap B')$

Example 4.5.12

Using a Venn Diagram to Draw Conclusions about Set Cardinality

In the Venn diagram below, the cardinality is listed in each section.

A two-set Venn diagram intersecting one another is given. The first set is labeled A while the second set is labeled B. Set A shows 7. Set B shows 5. The intersection of the sets shows 5. Outside the Venn diagram, it is marked U.

Find $n (A or B) .$
Find $n (A and B) .$
Find $n (A) .$

Answer

The number of elements in $A$ or $B$ is the number of elements in $A \cup B$ : $n (A \cup B) = 2 + 5 + 7 = 14 .$
The number of elements in $A$ and $B$ is the number of elements in $A \cap B$ : $n (A \cap B) = 5 .$
The number of elements in set $A$ is the sum of all the numbers enclosed in the circle representing set $A$ : $n (A) = 5 + 7 = 12 .$

Your Turn 4.5.12

The Venn diagram below shows the cardinality of each set.

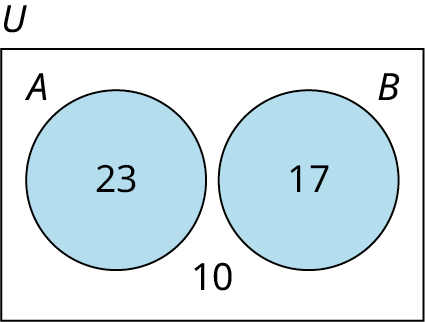
A two-set Venn diagram not intersecting one another is given. The first set is labeled A while the second set is labeled B. Set A shows 23. Set B shows 17. Outside the sets, 10 is given. Outside the Venn diagram, it is marked U.

Find n(A or B).
Find n(A and B).
Find n(A').

Learning Objectives

The Intersection of Two Sets

Intersection

Finding the Intersection of Set AA and Set BB

Determining the Intersection of Disjoint Sets

Finding the Intersection of a Set and a Subset

The Union of Two Sets

Union

Finding the Union of Sets AA and BB When AA and BB Overlap

Finding the Union of Sets AA and BB When AA and BB Are Disjoint

Finding the Union of Sets AA and BB When One Set is a Subset of the Other

Cardinality of the Union of Two Sets

Determining the Cardinality of the Union of Two Sets

Determining the Cardinality of the Union of Two Disjoint Sets

Applying Concepts of “AND” and “OR” to Set Operations

Applying the "AND" or "OR" Operation

Determine and Apply the Appropriate Set Operations to Solve the Problem

The Real Inventor of the Venn Diagram

Drawing Conclusions from a Venn Diagram with Two Sets

Using a Venn Diagram to Draw Conclusions about Set Membership

Using a Venn Diagram to Draw Conclusions about Set Cardinality

Finding the Intersection of Set $A$ and Set $B$

Finding the Union of Sets $A$ and $B$ When $A$ and $B$ Overlap

Finding the Union of Sets $A$ and $B$ When $A$ and $B$ Are Disjoint

Finding the Union of Sets $A$ and $B$ When One Set is a Subset of the Other