2.3: Equivalent Logical Statements
- Page ID
- 92957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we will analyze whether or not a statement is always true, always false, or sometimes true and sometimes false. We will also analyze two or more statements to determine whether they mean exactly the same thing.
Tautologies and Self-Contradictions
Consider the statements below.
- I am right or I am wrong.
- A number is odd or a number is not odd.
- It is snowing or it is not snowing.
- This apple is red or this apple is not red.
What do you notice about each statement?
Each statement is the disjunction of a statement and its negation. That is, each compound statement is formed by joining two simple statements that are opposite in meaning with the word 'or.'
Let's explore the first statement: I am right or I am wrong. We intuitively see that this statement will always be true, regardless of truth values of the simple statements that form it. Our intuition can be easy confirmed by constructing the truth table for the statement. Let \(p\) represent simple statement “I am right.” Then, \(\sim p\) represents “I am wrong”. The compound statement in symbolic form is represented by \( p \; \vee \sim p\). Recall the results of a truth table for a disjunction: the disjunction of two simple statements is always true unless both of the statements in the disjunction are false. The truth table is shown below.
\(\begin{array}{|c|c|c|}
\hline p & \sim p & p \; \vee \sim p \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T \vee F = T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F \vee T = T} \\
\hline
\end{array}\)
The last column of the truth table shows that \( p \; \vee \sim p\) is always true regardless of the truth values of the individual statements. This circumstance is called a tautology.
A tautology is compound statement that is always true regardless of the truth values of the individual statements.
Sometimes a compound statement may always be false regardless of the truth value of the individual statements. Let's change the previous statement from a disjunction to a conjunction and join two simple statements opposite in meaning with the word 'and'. We will create and analyze a truth table for the statement "I am right and I am wrong.”
Let \(p\) represent simple statement “I am right.” Then, \(\sim p\) represents “I am wrong”. The compound statement in symbolic form is represented by \( p \; \wedge \sim p\). Recall that a conjunction is true only in one case -- when both simple statements are true. Otherwise, a conjunction is false. The truth table is shown below.
\(\begin{array}{|c|c|c|}
\hline p & \sim p & p \; \wedge \sim p \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T \wedge F = F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F \wedge T = F} \\
\hline
\end{array}\)
The last column of the truth table shows that \( p \; \wedge \sim p\) is always false regardless of the truth values of the individual statements. This illustrates another special type of statement known as a self-contradiction.
A self-contradiction is compound statement that is always false regardless of the truth values of the individual statements.
Classify the statement as a tautology, a self–contradiction, or neither: \((p \wedge q) \rightarrow p\).
Solution
We need to construct and analyze a truth table. Recall the only case where a conditional statement is false is when the antecedent is true but the consequent is false (a broken promise.)
\(\begin{array}{|c|c|c|c|}
\hline p & q & p \wedge q & (p \wedge q) \rightarrow p \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T \wedge T = T} & \mathrm{T \rightarrow T = T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T \wedge F = F} & \mathrm{F \rightarrow T = T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F \wedge T = F} & \mathrm{F \rightarrow F = T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F \wedge F = F} & \mathrm{F \rightarrow F = T} \\
\hline
\end{array}\)
The last column shows that the compound statement \((p \wedge q) \rightarrow p\) is always true no matter what truth values are used for \(p\) and \(q\). Therefore, this statement is a tautology.
Classify the statement as a tautology, a self–contradiction, or neither: \(\sim (p \rightarrow q) \vee (q \rightarrow p)\).
Solution
Construct a truth table for this compound statement.
\(\begin{array}{|c|c|c|c|c|c|}
\hline p & q & p \rightarrow q & \sim (p \rightarrow q) & q \rightarrow p & \sim (p \rightarrow q) \vee (q \rightarrow p) \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T \rightarrow T =T} & \mathrm{F} & \mathrm{T \rightarrow T =T} & \mathrm{F \vee T = T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T \rightarrow F =F} & \mathrm{T} & \mathrm{F \rightarrow T =T} & \mathrm{T \vee T =T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F \rightarrow T =T} & \mathrm{F} & \mathrm{T \rightarrow F =F} & \mathrm{F \vee F =F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F \rightarrow F =T} & \mathrm{F} & \mathrm{F \rightarrow F =T} & \mathrm{F \vee T = T} \\
\hline
\end{array}\)
The last column shows that the compound statement \(\sim (p \rightarrow q) \vee (q \rightarrow p)\) is sometimes true and sometimes false. Therefore, this statement is a neither a tautology nor a self-contradiction.
Try it Now 1
Classify each statement as a tautology, a self–contradiction, or neither:
- \((p \vee q) \vee (\sim p \; \wedge \sim q)\)
- \((p \wedge q) \wedge (\sim p \; \vee \sim q)\)
- \((\sim p \rightarrow q) \leftrightarrow (p \wedge q)\)
- Answer
-
- tautology
- self-contradiction
- neither
Logically Equivalent Statements
On many occasions it is important to determine whether statements that are worded differently have the same meaning or not. To determine whether statements have exactly the same meaning, we construct truth tables and then compare the results.
Let's explore this idea with three similar, but differently worded, statements:
- I leave now or I am late.
- If I do not leave now, then I am late.
- If I leave now, then I am not late.
You may have an opinion about which, if any, of these statements have the same meaning, but only tools of formal logic allow us to make a sure conclusion about whether they mean the same.
Here, we let \(p\) represent the simple statement "I leave now" and \(q\) represent "I am late." The three compound statements can be presented symbolically as
- \(p \vee q\)
- \(\sim p \rightarrow q\)
- \(p \rightarrow \; \sim q\)
We construct truth tables for each of the three compound statements.
| A: \(p \vee q\) | B: \(\sim p \rightarrow q\) | C: \(p \rightarrow \; \sim q\) |
|---|---|---|
| \(\begin{array}{|c|c|c|} \hline p & q & p \vee q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T \vee T = T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T \vee F = T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F \vee T = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F \vee F = F} \\ \hline \end{array}\) |
\(\begin{array}{|c|c|c|c|} \hline p & q & \sim p & \sim p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F \rightarrow T = T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F \rightarrow F = T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T \rightarrow T = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T \rightarrow F = F} \\ \hline \end{array}\) |
\(\begin{array}{|c|c|c|c|} \hline p & q & \sim q & p \rightarrow \; \sim q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T \rightarrow F = F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T \rightarrow T = T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F \rightarrow F = T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F \rightarrow T = T} \\ \hline \end{array}\) |
Comparing the last columns of the three truth tables, we see that Statement A and Statement B have exactly the same truth values for all possible truth values of simple statements. This means that statements A and B are logically equivalent. They have exactly the same meaning.
However, Statement C is not logically equivalent to Statements A and B. Statement C sometimes means something different than Statements A and B.
Here, we say \(p \vee q\) is logically equivalent to \(\sim p \rightarrow q\). To illustrate how this works verbally, "You use an umbrella or you'll get soaked" means the same as "If you don't use an umbrella, then you'll get soaked."
Two compound statements are logically equivalent if and only if the statements have the same truth values for all possible combinations of truth values for the simple statements that form them.
The symbol commonly used to show two statements are logically equivalent is \(\Leftrightarrow\). This symbol \(\equiv\) may also be used.
Decide if the statements \(\sim (p \vee q)\) and \(\sim p \; \wedge \sim q\) are logically equivalent.
Solution
We construct and compare the truth tables for each statement.
| \(\begin{array}{|c|c|c|c|} \hline p & q & p \vee q & \sim (p \vee q) \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T \vee T = T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T \vee F = T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F \vee T = T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F \vee F = F} & \mathrm{ T} \\ \hline \end{array}\) |
\(\begin{array}{|c|c|c|c|c|} \hline p & q & \sim p & \sim q & \sim p \; \wedge \sim q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F \wedge F = F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F \wedge T = F}\\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T \wedge F = F}\\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{ T} & \mathrm{T \wedge T = T}\\ \hline \end{array}\) |
Since both statements have the same resulting truth values in the last columns of their truth tables, the statements are logically equivalent and we can write
\(\sim (p \vee q)\ \Leftrightarrow \; \sim p \; \wedge \sim q\)
This equivalence can be described verbally as "The negation of a disjunction is equivalent to the conjunction of the negations" and is one of DeMorgan's Laws of Logic.
Try it Now 2
Construct truth tables to show \(\sim (p \wedge q) \; \Leftrightarrow \; \sim p \; \vee \sim q\). Then, describe the equivalence in words.
- Answer
-
Truth Tables for \(\sim (p \wedge q) \) and \( \sim p \; \vee \sim q\). \(\begin{array}{|c|c|c|c|}
\hline p & q & p \wedge q & \sim (p \wedge q) \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T \wedge T = T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T \vee F = F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F \wedge T = F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F \wedge F = F} & \mathrm{ T} \\
\hline
\end{array}\)\(\begin{array}{|c|c|c|c|c|}
\hline p & q & \sim p & \sim q & \sim p \; \vee \sim q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F \vee F = F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F \vee T = T}\\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T \vee F = T}\\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{ T} & \mathrm{T \vee T = T}\\
\hline
\end{array}\)Both statements have the same resulting truth values in the last columns of their truth tables, so \(\sim (p \wedge q)\ \; \Leftrightarrow \; \; \sim p \; \vee \sim q\). This equivalence can be verbally described as "The negation of a conjunction is equivalent to the disjunction of the negations" and is the second of DeMorgan's Laws of Logic.
We have now proven both of DeMorgan's Laws of Logic.
\(\sim (p \vee q)\ \; \Leftrightarrow \; \; \sim p \; \wedge \sim q\)
\(\sim (p \wedge q)\ \; \Leftrightarrow \; \; \sim p \; \vee \sim q\)
Use DeMorgan's Laws to write a statement equivalent to “It is false that I am taking geometry or I am taking biology.”
Solution
First, write the statement in symbolic form. Let \(p\) represent the statement "I take geometry" and \(q\) represent the statement "I take biology." So, the statement is presented as \(\sim (p \vee q)\).
Using the first of DeMorgan Laws, the negation of a disjunction is the conjunction of the negations. Or, \(\sim (p \vee q)\) is equivalent to \(\sim p \; \wedge \sim q\).
The statement \(\sim p \; \wedge \sim q\) can be translated to words as “I am not taking geometry and I am not taking biology.
Try it Now 3
Use one of DeMorgan's Laws to write a statement equivalent to “The dog is small and the dog barks loudly.”
- Answer
-
It is false that the dog is small or it barks loudly.
Several other useful equivalencies can be proven using truth tables. One relates a conditional statement and a disjunction, and another relates the negation of a conditional statement and a conjunction. They are presented here.
\(p \rightarrow q \Leftrightarrow \; \sim p \; \vee q\)
\(\sim (p \rightarrow q) \Leftrightarrow \; p \; \wedge \sim q\)
Write the following statement as a disjunction: If I am tired, then I am sleepy.
Solution
The given statement is a conditional statement and can be written as \(p \rightarrow q\) where \(p\) is the statement "I am tired" and \(q\) is the statement "I am sleepy."
Using the equivalency \(p \rightarrow q \Leftrightarrow \; \sim p \; \vee q\), the statement can be rewritten as “I am not tired or I am sleepy”.
Try it Now 4
Write the negation of the statement “If I am tired, then I am sleepy” as a conjunction using the equivalency \(\sim (p \rightarrow q) \Leftrightarrow \; p \; \wedge \sim q\).
- Answer
-
I am tired but I am not sleepy.
You may also say... I am tired and I am not sleepy.
Variations of the Conditional Statement
Variations of conditional statements play a big role in mathematical proofs as well as in writing various IF – ELSE logical flow operators in programming languages. The variations of a conditional statement are the converse of the conditional, the inverse of the conditional, and the contrapositive of the conditional.
| Name | Symbolic Form | In Words |
|---|---|---|
| Conditional | \(p \rightarrow q\) | If \(p\), then \(q\). |
| Converse | \(q \rightarrow p\) | If \(q\), then \(p\). |
| Inverse | \(\sim p \rightarrow \; \sim q\) | If \(\sim p\), then \(\sim q\). |
| Contrapositive | \(\sim q \rightarrow \; \sim p\) | If \(\sim q\), then \(\sim p\). |
Write the converse, inverse, and contrapositive to the conditional statement “If I work diligently, then I will gain understanding.”
Solution
Let \(p\) represent “I work diligently” and \(q\) represent “I gain understanding.”
The converse \(q \rightarrow p\) is “If I gain understanding, then I work diligently.”
The inverse \(\sim p \rightarrow \; \sim q\) is “If I do not work diligently then I will not gain understanding.”
The contrapositive \(\sim q \rightarrow \; \sim p\) is “If I do not gain understanding, then I will not work diligently."
Be aware that symbolic logic cannot represent the English language perfectly. For example, we may need to change the verb tense to show that one thing occurred before another.
Write the converse, inverse, and contrapositive to the conditional statement “If I teach third grade, then I am an elementary teacher”.
Solution
Let \(p\) represent “I teach third grade” and \(q\) represent “I am an elementary teacher.”
The converse \(q \rightarrow p\) is “If I am an elementary teacher, then I teach third grade.”
The inverse \(\sim p \rightarrow \; \sim q\) is “If I don't teach third grade, then I am not an elementary teacher.”
The contrapositive \(\sim q \rightarrow \; \sim p\) is “If I am not an elementary teacher, then I don't teach third grade."
Try it Now 5
For each conditional statement, write the indicated statement related to the conditional.
- If it is raining, then I wear a raincoat. (inverse)
- If I confess, then I am guilty. (contrapositive)
- If I drive a truck, then I need a driver’s license. (converse)
- If I make less than 60%, then I won’t pass the test. (contrapositive)
- Answer
-
- If it is not raining, then I don't wear a raincoat.
- If I am not guilty, then I won't confess.
- If I need a driver's licenses, then I drive a truck.
- If I passed the test, then I didn't make less than 60%.
Equivalencies Involving the Conditional Statement and Its Variations
Once looking at a conditional statement and its variations, a natural question to ask is whether or not any of these statements mean the same thing. In other words, are any of the four statements - the conditional, its converse, its inverse, and its contrapositive - logically equivalent? If any of the statements are logically equivalent, then we can substitute one for the other without changing the meaning. Sometimes it can be helpful to make a complicated statement more clear by rewriting it using an logically equivalent variation.
Looking back at Example 7, you can see that the conditional statement "If I I teach third grade, then I am an elementary teacher" does not mean the same as its converse "If I am elementary teacher, then I teach third grade." They are not logically equivalent because it is possible for the conditional statement to be true while at the same time the converse to be be false. It is possible that someone is an elementary teacher but not teach third grade. That is, the person might teach second grade. This example shows us that a conditional and its converse are not necessarily logically equivalent.
However, looking at truth tables below, we can see that the original conditional statement and its contrapositive are logically equivalent. We can also see that its converse and inverse are logically equivalent.
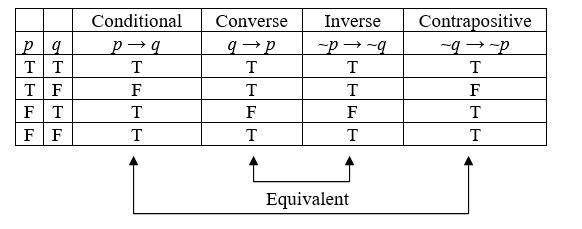
A conditional statement and its contrapositive are logically equivalent: \(p \rightarrow q \: \: \Leftrightarrow \; \: \sim q \rightarrow \; \sim p\).
The converse and inverse of a conditional statement are logically equivalent: \(q \rightarrow p \: \: \Leftrightarrow \; \: \sim p \rightarrow \; \sim q\).
In other words, the original statement and the contrapositive must agree with each other. They must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other. They must both be true, or they must both be false.
Also, recall that we have already proven that the conditional \(p \rightarrow q\) can be rewritten as disjunction \(\sim p \; \vee q\). Therefore, the following three statements are logically equivalent:
\(p \rightarrow q \; \; \; \Leftrightarrow \; \; \; \; \sim q \rightarrow \: \sim p \; \; \; \Leftrightarrow \; \; \; \; \sim p \vee q\)
We now will use the equivalencies discussed in this section to solve problems.
Suppose the following statement is true: If it rains today, then I will scream.
Which of the following must also be true?
- If I do not scream, then it is not raining.
- If I scream, then it is raining today.
- If it does not rain today, then I will not scream.
Solution
We let \(p\) represent "It rains" and \(q\) represent "I scream." The original conditional statement takes the form of \(p \rightarrow q\).
- "If I do not scream, then it is not raining" can be translated to \(\sim q \rightarrow \; \sim p\). This is the contrapositive and is equivalent to the conditional. So, if the original conditional statement is true, so is this statement.
- "If I scream, then it is raining today" can be translated to \(q \rightarrow p\). This is the converse and is not equivalent to the conditional. So, if the conditional statement is true, we cannot say that this statement is also necessarily true. It may or may not be true.
- "If it does not rain today, then I will not scream" can be translated to \(\sim p \rightarrow \; \sim q\). This is the inverse and is not equivalent to the conditional. So, if the conditional statement is true, we cannot say that this statement is also necessarily true. It may or may not be true.
Rewrite the statement "If I’m not happy, then there isn’t a puppy in the house" as a simpler, but logically equivalent, conditional statement.
Solution
This conditional statement is awkward and difficult to think about since it contains the word "not" twice. Recall that its contrapositive is logically equivalent to a conditional statement. Rewriting the statement with its contrapositive perhaps will make the meaning more clear.
We let \(p\) represent "I'm not happy" and \(q\) represent "There isn't a puppy in the house." The original conditional statement takes the form of \(p \rightarrow q\) and the contrapositive takes on the form \(\sim q \rightarrow \; \sim p\).
A less cumbersome way to make this statement is "If there is a puppy in the house, then I am happy."
Try it Now 6
Suppose the following statement is true: “If you microwave salmon in the staff kitchen, then I will be mad at you.”
If this statement is true, which of the following statements must also be true? Be sure to give a reason for your answer.
- If you don’t microwave salmon in the staff kitchen, then I won’t be mad at you.
- If I am not mad at you, then you didn’t microwave salmon in the staff kitchen.
- If I am mad at you, then you microwaved salmon in the staff kitchen.
- You didn't microwave salmon in the staff kitchen or I am mad at you.
- Answer
-
Statements b and d must also be true. Statement b is the contrapositive of the original statement. Statement d is the original conditional statement rewritten as a disjunction: \(p \rightarrow q \Leftrightarrow \; \sim p \; \vee q\).


