1.6: Absolute Value Functions
- Page ID
- 117101
Understanding Absolute Value
Recall that in its basic form \(f(x)=|x|\), the absolute value function, is one of our toolkit functions. The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign.
The absolute value function can be defined as a piecewise function
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Describe all values \(x\) within or including a distance of 4 from the number 5.
Solution
We want the distance between \(x\) and 5 to be less than or equal to 4. We can draw a number line, such as the one in , to represent the condition to be satisfied.

The distance from \(x\) to 5 can be represented using the absolute value as \(|x−5|\). We want the values of \(x\) that satisfy the condition \(| x−5 |\leq4\).
Analysis
Note that
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
So \(|x−5|\leq4\) is equivalent to \(1{\leq}x\leq9\).
However, mathematicians generally prefer absolute value notation.
Solving an Absolute Value Inequality
Absolute value equations may not always involve equalities. Instead, we may need to solve an equation within a range of values. We would use an absolute value inequality to solve such an equation. An absolute value inequality is an equation of the form
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
or
\[ |A|{\geq}B, \nonumber\]
where an expression \(A\) (and possibly but not usually \(B\)) depends on a variable \(x\). Solving the inequality means finding the set of all \(x\) that satisfy the inequality. Usually this set will be an interval or the union of two intervals.
There are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is we can read the solution by interpreting the graphs of two functions. The advantage of the algebraic approach is it yields solutions that may be difficult to read from the graph.
For example, we know that all numbers within 200 units of 0 may be expressed as
\[|x|<200 \nonumber\]
or
\[ −200<x<200 \nonumber\]
Suppose we want to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We can solve algebraically for the set of values \(x\) such that the distance between \(x\) and 600 is less than 200. We represent the distance between \(x\) and 600 as \(|x−600|\).
\[|x−600|<200\]
or
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
This means our returns would be between $400 and $800.
Sometimes an absolute value inequality problem will be presented to us in terms of a shifted and/or stretched or compressed absolute value function, where we must determine for which values of the input the function’s output will be negative or positive.
Given an absolute value inequality of the form \(|x−A|{\leq}B\) for real numbers \(a\) and \(b\) where \(b\) is positive, solve the absolute value inequality algebraically.
- Find boundary points by solving \(|x−A|=B\).
- Test intervals created by the boundary points to determine where \(|x−A|{\leq}B\).
- Write the interval or union of intervals satisfying the inequality in interval, inequality, or set-builder notation.
Solve \(|x −5|{\leq}4\).
Solution
With both approaches, we will need to know first where the corresponding equality is true. In this case we first will find where \(|x−5|=4\). We do this because the absolute value is a function with no breaks, so the only way the function values can switch from being less than 4 to being greater than 4 is by passing through where the values equal 4. Solve \(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
After determining that the absolute value is equal to 4 at \(x=1\) and \(x=9\), we know the graph can change only from being less than 4 to greater than 4 at these values. This divides the number line up into three intervals:
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
To determine when the function is less than 4, we could choose a value in each interval and see if the output is less than or greater than 4, as shown in Table \(\PageIndex{1}\).
| Interval test \(x\) | \(f(x)\) | \(<4\) or \(>4\) | |
|---|---|---|---|
| \(x<1\) | 0 | \(|0-5|=5\) | Greater than |
| \(1<x<9\) | 6 | \(|6-5|=1\) | Less than |
| \(x>9\) | 11 | \(|11-5|=6\) | Greater than |
Because \(1{\leq}x{\leq}9\) is the only interval in which the output at the test value is less than 4, we can conclude that the solution to \(|x−5|{\leq}4\) is \(1{\leq}x{\leq}9\), or \([1,9]\).
To use a graph, we can sketch the function \(f(x)=|x−5|\). To help us see where the outputs are 4, the line \(g(x)=4\) could also be sketched as in Figure \(\PageIndex{11}\).
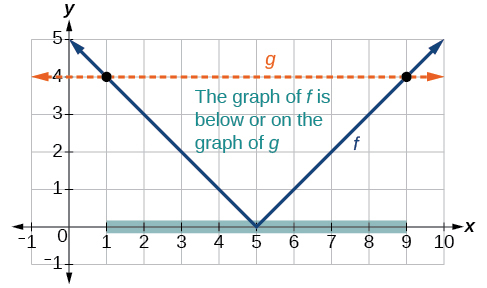
We can see the following:
- The output values of the absolute value are equal to 4 at \(x=1\) and \(x=9\).
- The graph of \(f\) is below the graph of \(g\) on \(1<x<9\). This means the output values of \(f(x)\) are less than the output values of \(g(x)\).
- The absolute value is less than or equal to 4 between these two points, when \(1{\leq}x\leq9\). In interval notation, this would be the interval \([1,9]\).
Analysis
For absolute value inequalities,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
The \(<\) or \(>\) symbol may be replaced by \(\leq\) or \(\geq\).
So, for this example, we could use this alternative approach.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]


