5.1: Angles
- Page ID
- 117139
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Drawing Angles in Standard Position
Properly defining an angle first requires that we define a ray. A ray consists of one point on a line and all points extending in one direction from that point. The first point is called the endpoint of the ray. We can refer to a specific ray by stating its endpoint and any other point on it. The ray in Figure \(\PageIndex{1}\) can be named as ray EF, or in symbol form \(\overrightarrow{EF}\).
An angle is the union of two rays having a common endpoint. The endpoint is called the vertex of the angle, and the two rays are the sides of the angle. The angle in Figure \(\PageIndex{2}\) is formed from \(\overrightarrow{ED}\) and \(\overrightarrow{EF}\). Angles can be named using a point on each ray and the vertex, such as angle DEF, or in symbol form \(∠DEF.\)
Greek letters are often used as variables for the measure of an angle. Table \(\PageIndex{1}\) is a list of Greek letters commonly used to represent angles, and a sample angle is shown in Figure \(\PageIndex{3}\).
| \(θ\) | \(φ \text{ or }ϕ\) | \(α\) | \(β\) | \(γ\) |
| theta | phi | alpha | beta | gamma |
Figure \(\PageIndex{3}\): Angle theta, shown as \(∠θ\)
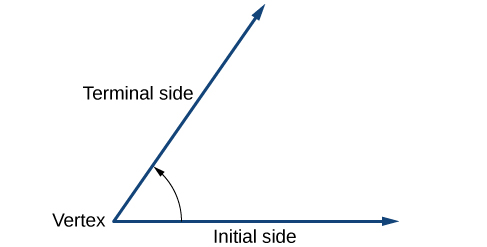
Angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side, and the rotated ray is the terminal side. In order to identify the different sides, we indicate the rotation with a small arc and arrow close to the vertex as in Figure \(\PageIndex{4}\).
As we discussed at the beginning of the section, there are many applications for angles, but in order to use them correctly, we must be able to measure them. The measure of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. One degree is \(\frac{1}{360}\) of a circular rotation, so a complete circular rotation contains 360 degrees. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol °. For example, 90 degrees = 90°.
To formalize our work, we will begin by drawing angles on an x-y coordinate plane. Angles can occur in any position on the coordinate plane, but for the purpose of comparison, the convention is to illustrate them in the same position whenever possible. An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. See Figure \(\PageIndex{5}\).
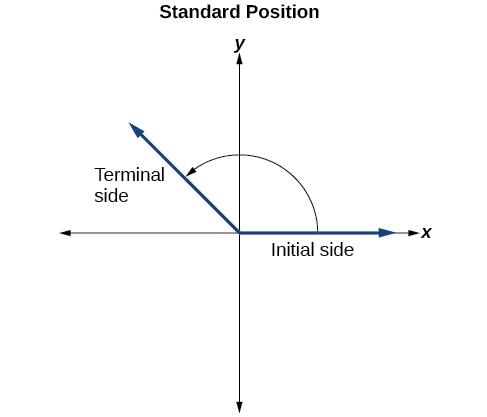
If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle. If the angle is measured in a clockwise direction, the angle is said to be a negative angle.
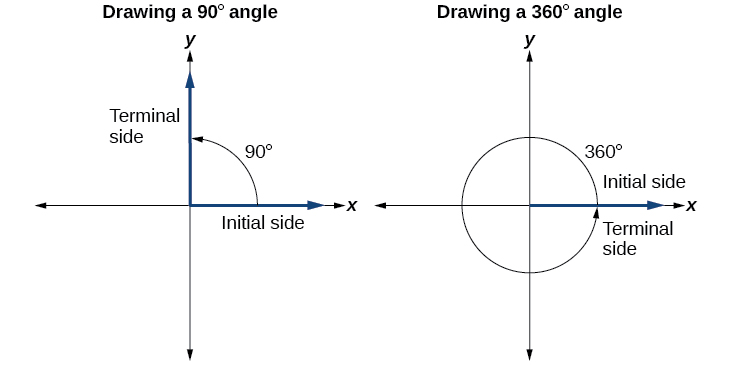
Drawing an angle in standard position always starts the same way—draw the initial side along the positive x-axis. To place the terminal side of the angle, we must calculate the fraction of a full rotation the angle represents. We do that by dividing the angle measure in degrees by 360°. For example, to draw a 90° angle, we calculate that \(\frac{90°}{360°}=\frac{1}{4}\). So, the terminal side will be one-fourth of the way around the circle, moving counterclockwise from the positive x-axis. To draw a 360° angle, we calculate that \(\frac{360°}{360°}=1\). So the terminal side will be 1 complete rotation around the circle, moving counterclockwise from the positive x-axis. In this case, the initial side and the terminal side overlap. See Figure \(\PageIndex{6}\) .
Since we define an angle in standard position by its initial side, we have a special type of angle whose terminal side lies on an axis, a quadrantal angle. This type of angle can have a measure of 0°, 90°, 180°, 270° or 360°. See Figure \(\PageIndex{7}\).
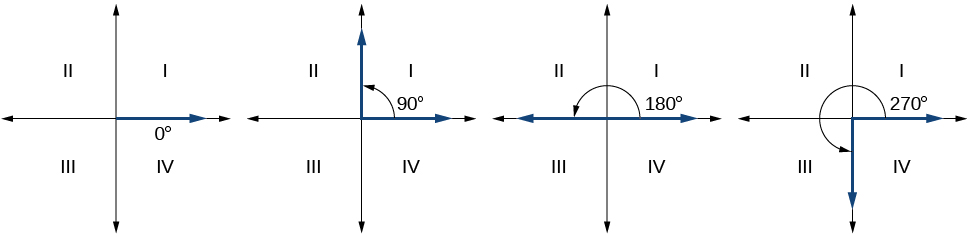
Quadrantal angles are angles in standard position whose terminal side lies on an axis, including 0°, 90°, 180°, 270°, or 360°.
- Express the angle measure as a fraction of 360°.
- Reduce the fraction to simplest form.
- Draw an angle that contains that same fraction of the circle, beginning on the positive x-axis and moving counterclockwise for positive angles and clockwise for negative angles.
- Sketch an angle of 30° in standard position.
- Sketch an angle of −135° in standard position.
Solution
- Divide the angle measure by 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]
To rewrite the fraction in a more familiar fraction, we can recognize that
\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]
One-twelfth equals one-third of a quarter, so by dividing a quarter rotation into thirds, we can sketch a line at 30° as in Figure \(\PageIndex{8}\).
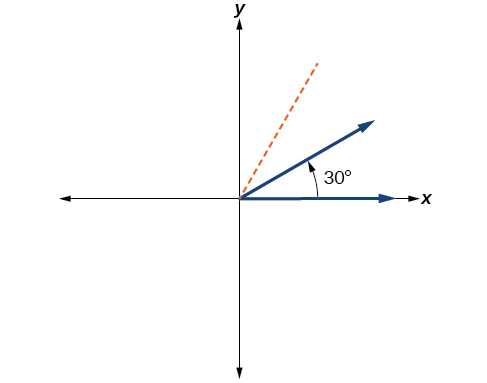
Figure \(\PageIndex{8}\) - Divide the angle measure by 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]
In this case, we can recognize that
\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]
Negative three-eighths is one and one-half times a quarter, so we place a line by moving clockwise one full quarter and one-half of another quarter, as in Figure \(\PageIndex{9}\).
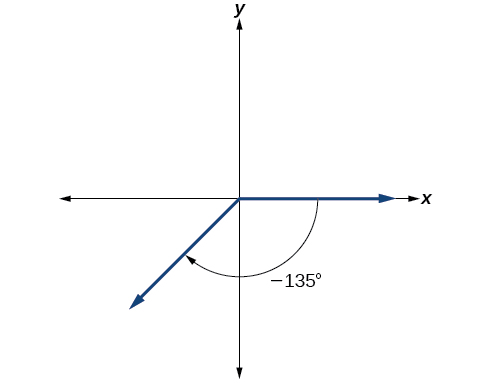
Figure \(\PageIndex{9}\)
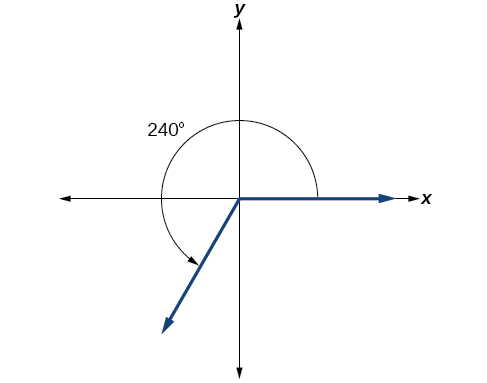
Show an angle of 240° on a circle in standard position.
Solution
Converting Between Degrees and Radians
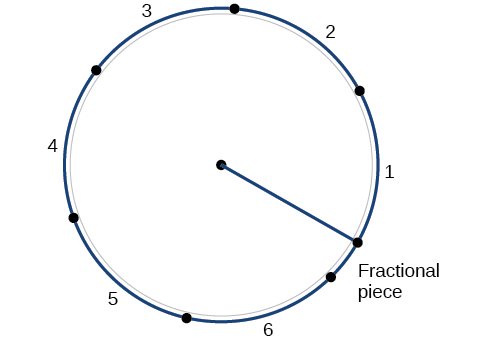
Dividing a circle into 360 parts is an arbitrary choice, although it creates the familiar degree measurement. We may choose other ways to divide a circle. To find another unit, think of the process of drawing a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circle, a full circle, or more than a full circle, represented by more than one full rotation. The length of the arc around an entire circle is called the circumference of that circle.
The circumference of a circle is \(C=2πr\). If we divide both sides of this equation by \(r\), we create the ratio of the circumference to the radius, which is always \(2π\) regardless of the length of the radius. So the circumference of any circle is \(2π≈6.28\) times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in Figure \(\PageIndex{11}\).
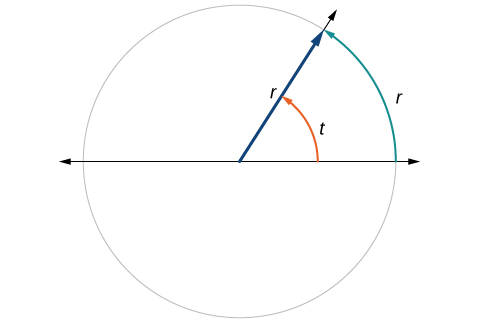
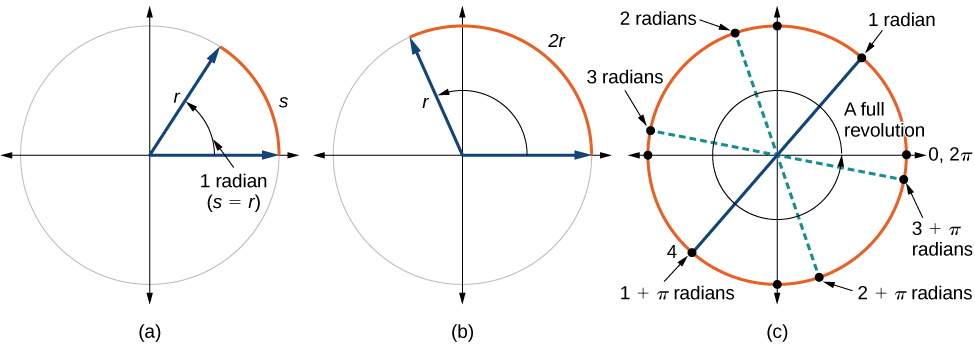
This brings us to our new angle measure. One radian is the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle. A central angle is an angle formed at the center of a circle by two radii. Because the total circumference equals \(2π\) times the radius, a full circular rotation is \(2π\) radians. So
\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]
See Figure \(\PageIndex{12}\). Note that when an angle is described without a specific unit, it refers to radian measure. For example, an angle measure of 3 indicates 3 radians. In fact, radian measure is dimensionless, since it is the quotient of a length (circumference) divided by a length (radius) and the length units cancel out.
Relating Arc Lengths to Radius
An arc length \(s\) is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius.
This ratio, called the radian measure, is the same regardless of the radius of the circle—it depends only on the angle. This property allows us to define a measure of any angle as the ratio of the arc length s s to the radius \(r\). See Figure \(\PageIndex{13}\).
\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]
If \( s=r\), then \(θ=\frac{r}{r}= 1 \text{ radian.}\)
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is \(C=2πr\),where \(r\) is the radius. The smaller circle then has circumference \(2π(2)=4π\) and the larger has circumference \(2π(3)=6π\). Now we draw a 45° angle on the two circles, as in Figure \(\PageIndex{14}\).
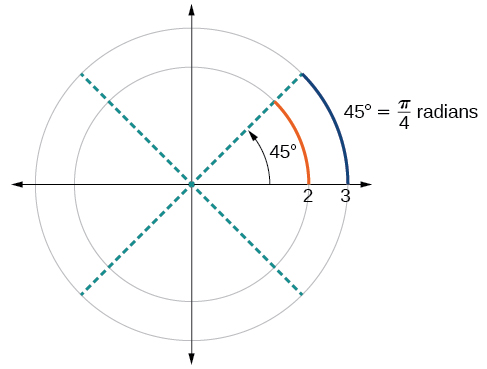
Notice what happens if we find the ratio of the arc length divided by the radius of the circle.
\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]
Since both ratios are \(\frac{1}{4}π\), the angle measures of both circles are the same, even though the arc length and radius differ.
One radian is the measure of the central angle of a circle such that the length of the arc between the initial side and the terminal side is equal to the radius of the circle. A full revolution (360°) equals \(2\pi\) radians. A half revolution (180°) is equivalent to \(\pi\) radians.
The radian measure of an angle is the ratio of the length of the arc subtended by the angle to the radius of the circle. In other words, if \(s\) is the length of an arc of a circle, and \(r\) is the radius of the circle, then the central angle containing that arc measures \(\frac{s}{r}\) radians. In a circle of radius 1, the radian measure corresponds to the length of the arc.
Using Radians
Because radian measure is the ratio of two lengths, it is a unitless measure. For example, in Figure \(\PageIndex{14}\), suppose the radius were 2 inches and the distance along the arc were also 2 inches. When we calculate the radian measure of the angle, the “inches” cancel, and we have a result without units. Therefore, it is not necessary to write the label “radians” after a radian measure, and if we see an angle that is not labeled with “degrees” or the degree symbol, we can assume that it is a radian measure.
Considering the most basic case, the unit circle (a circle with radius 1), we know that 1 rotation equals 360 degrees, 360°. We can also track one rotation around a circle by finding the circumference, \(C=2πr\), and for the unit circle \(C=2π.\) These two different ways to rotate around a circle give us a way to convert from degrees to radians.
\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]
Identifying Special Angles Measured in Radians
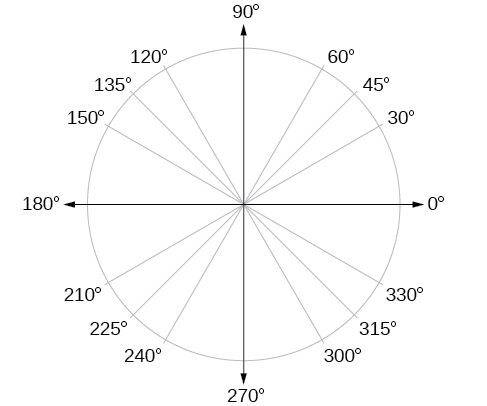
In addition to knowing the measurements in degrees and radians of a quarter revolution, a half revolution, and a full revolution, there are other frequently encountered angles in one revolution of a circle with which we should be familiar. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown in Figure \(\PageIndex{15}\). Memorizing these angles will be very useful as we study the properties associated with angles.
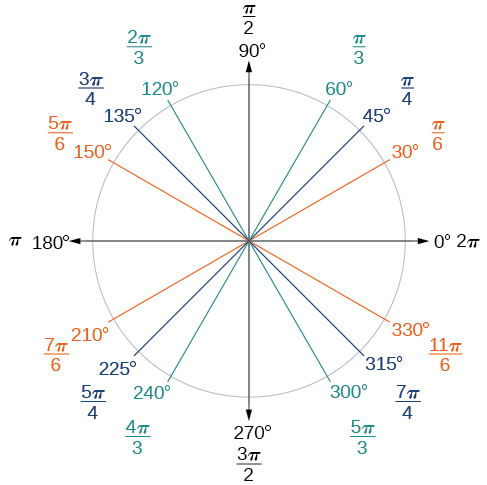
Now, we can list the corresponding radian values for the common measures of a circle corresponding to those listed in Figure \(\PageIndex{15}\), which are shown in Figure \(\PageIndex{16}\). Be sure you can verify each of these measures.
Converting between Radians and Degrees
Because degrees and radians both measure angles, we need to be able to convert between them. We can easily do so using a proportion.
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
This proportion shows that the measure of angle \(θ\) in degrees divided by 180 equals the measure of angle \(θ\) in radians divided by \(π.\) Or, phrased another way, degrees is to 180 as radians is to \(π\).
\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]
To convert between degrees and radians, use the proportion
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Finding Coterminal Angles
Converting between degrees and radians can make working with angles easier in some applications. For other applications, we may need another type of conversion. Negative angles and angles greater than a full revolution are more awkward to work with than those in the range of 0° to 360°, or 0 to \(2π\). It would be convenient to replace those out-of-range angles with a corresponding angle within the range of a single revolution.
It is possible for more than one angle to have the same terminal side. Look at Figure \(\PageIndex{17}\). The angle of 140° is a positive angle, measured counterclockwise. The angle of –220° is a negative angle, measured clockwise. But both angles have the same terminal side. If two angles in standard position have the same terminal side, they are coterminal angles. Every angle greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and it is often more convenient to find the coterminal angle within the range of 0° to 360° than to work with an angle that is outside that range.
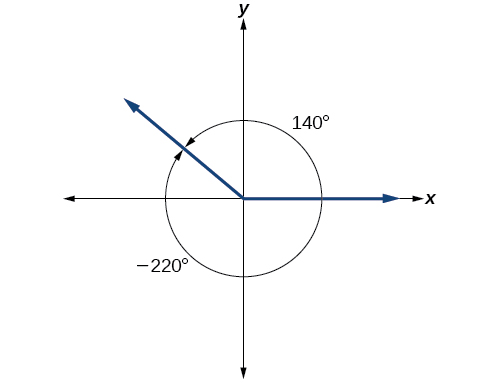
Any angle has infinitely many coterminal angles because each time we add 360° to that angle—or subtract 360° from it—the resulting value has a terminal side in the same location. For example, 100° and 460° are coterminal for this reason, as is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.
An angle’s reference angle is the measure of the smallest, positive, acute angle \(t\) formed by the terminal side of the angle \(t\) and the horizontal axis. Thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. See Figure \(\PageIndex{18}\) for examples of reference angles for angles in different quadrants.
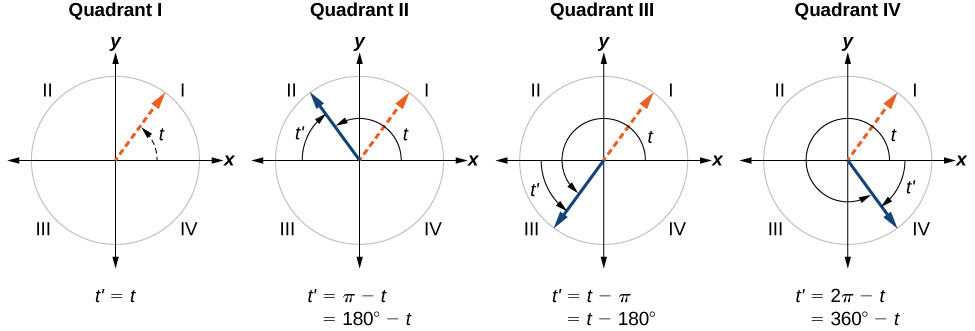
- Coterminal angles are two angles in standard position that have the same terminal side.
- An angle’s reference angle is the size of the smallest acute angle, \(t′\), formed by the terminal side of the angle \(t\) and the horizontal axis.
- Subtract 360° from the given angle.
- If the result is still greater than 360°, subtract 360° again till the result is between 0° and 360°.
- The resulting angle is coterminal with the original angle.
Finding Coterminal Angles Measured in Radians
We can find coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, we find coterminal angles by adding or subtracting one or more full rotations.
- Subtract \(2π\) from the given angle.
- If the result is still greater than \(2π\), subtract \(2π\) again until the result is between \(0\) and \(2π\).
- The resulting angle is coterminal with the original angle.
Determining the Length of an Arc
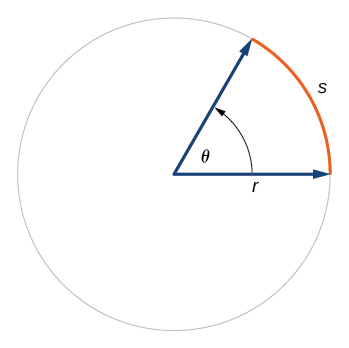
Recall that the radian measure \(θ\) of an angle was defined as the ratio of the arc length \(s\) of a circular arc to the radius \(r\) of the circle, \(θ=\frac{s}{r}\). From this relationship, we can find arc length along a circle, given an angle.
In a circle of radius r, the length of an arc \(s\) subtended by an angle with measure \(θ\) in radians, shown in Figure \(\PageIndex{22}\), is
\[s=rθ\]
- If necessary, convert \(θ\) to radians.
- Multiply the radius \(r\) by the radian measure of \(θ:s=rθ\).
Assume the orbit of Mercury around the sun is a perfect circle. Mercury is approximately 36 million miles from the sun.
- In one Earth day, Mercury completes 0.0114 of its total revolution. How many miles does it travel in one day?
- Use your answer from part (a) to determine the radian measure for Mercury’s movement in one Earth day.
Solution
- Let’s begin by finding the circumference of Mercury’s orbit.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]
Since Mercury completes 0.0114 of its total revolution in one Earth day, we can now find the distance traveled:
\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
- Now, we convert to radians:
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]
Finding the Area of a Sector of a Circle
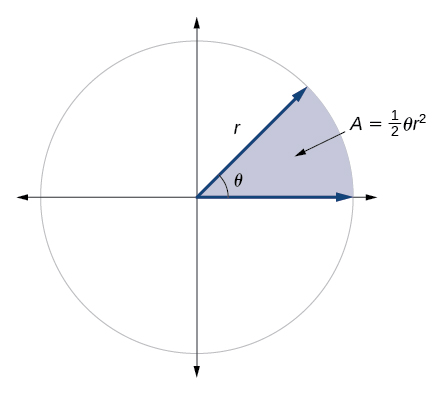
In addition to arc length, we can also use angles to find the area of a sector of a circle. A sector is a region of a circle bounded by two radii and the intercepted arc, like a slice of pizza or pie. Recall that the area of a circle with radius \(r\) can be found using the formula \(A=πr^2\). If the two radii form an angle of \(θ\), measured in radians, then \(\frac{θ}{2π}\) is the ratio of the angle measure to the measure of a full rotation and is also, therefore, the ratio of the area of the sector to the area of the circle. Thus, the area of a sector is the fraction \(\frac{θ}{2π}\) multiplied by the entire area. (Always remember that this formula only applies if \(θ\) is in radians.)
\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]
The area of a sector of a circle with radius \(r\) subtended by an angle \(θ\), measured in radians, is
\[A=\dfrac{1}{2}θr^2\]
See Figure \(\PageIndex{23}\).
- If necessary, convert \(θ\) to radians.
- Multiply half the radian measure of \(θ\) by the square of the radius \(r: A=\frac{1}{2}θr^2.\)
Use Linear and Angular Speed to Describe Motion on a Circular Path
In addition to finding the area of a sector, we can use angles to describe the speed of a moving object. An object traveling in a circular path has two types of speed. Linear speed is speed along a straight path and can be determined by the distance it moves along (its displacement) in a given time interval. For instance, if a wheel with radius 5 inches rotates once a second, a point on the edge of the wheel moves a distance equal to the circumference, or 10π inches, every second. So the linear speed of the point is \(10π\) in./s. The equation for linear speed is as follows where \(v\) is linear speed, \(s\) is displacement, and \(t\) is time.
\[v=\dfrac{s}{t}\]
Angular speed results from circular motion and can be determined by the angle through which a point rotates in a given time interval. In other words, angular speed is angular rotation per unit time. So, for instance, if a gear makes a full rotation every 4 seconds, we can calculate its angular speed as \(\frac{360 \text{ degrees}}{4 \text{ seconds}}= \) 90 degrees per second. Angular speed can be given in radians per second, rotations per minute, or degrees per hour for example. The equation for angular speed is as follows, where \(ω\) (read as omega) is angular speed, \(θ\) is the angle traversed, and \(t\) is time.
\[ω=\dfrac{θ}{t}\]
Combining the definition of angular speed with the arc length equation, \(s=rθ\), we can find a relationship between angular and linear speeds. The angular speed equation can be solved for \(θ\), giving \(θ=ωt.\) Substituting this into the arc length equation gives:
\[\begin{align}s &=rθ \\ &=rωt \end{align}\]
Substituting this into the linear speed equation gives:
\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]
As a point moves along a circle of radius \(r,\) its angular speed, \(ω\), is the angular rotation \(θ\) per unit time, \(t\).
\[ω=\dfrac{θ}{t}\]
The linear speed. \(v\), of the point can be found as the distance traveled, arc length \(s\), per unit time, \(t.\)
\[v=\frac{s}{t}\]
When the angular speed is measured in radians per unit time, linear speed and angular speed are related by the equation
\[v=rω\]
This equation states that the angular speed in radians, \(ω\), representing the amount of rotation occurring in a unit of time, can be multiplied by the radius \(r\) to calculate the total arc length traveled in a unit of time, which is the definition of linear speed.
- If necessary, convert the angle measure to radians.
- Divide the angle in radians by the number of time units elapsed: \(ω=\frac{θ}{t}.\)
- The resulting speed will be in radians per time unit.


