5.4: Right Triangle Trigonometry

Last updated
Save as PDF

Page ID: 117142

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions. In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x-axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

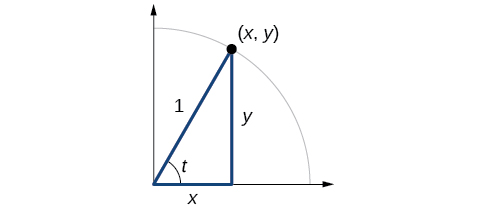
Graph of quarter circle with radius of 1. Inscribed triangle with an angle of t. Point of (x,y) is at intersection of terminal side of angle and edge of circle. — Figure \(\PageIndex{1}\)

We know

\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse. These sides are labeled in Figure \(\PageIndex{2}\).

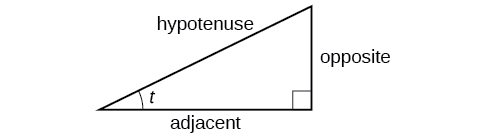
A right triangle with hypotenuse, opposite, and adjacent sides labeled. — Figure \(\PageIndex{2}\): The sides of a right triangle in relation to angle \(t\).

Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

Find the sine as the ratio of the opposite side to the hypotenuse.
Find the cosine as the ratio of the adjacent side to the hypotenuse.
Find the tangent is the ratio of the opposite side to the adjacent side.

Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

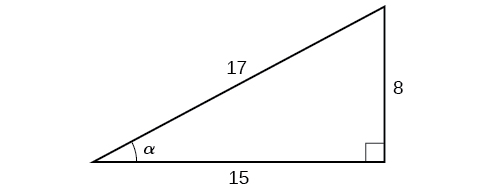
A right triangle with side lengths of 8, 15, and 17. Angle alpha also labeled which is opposite to the side labeled 8. — Figure \(\PageIndex{3}\)

Solution

The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

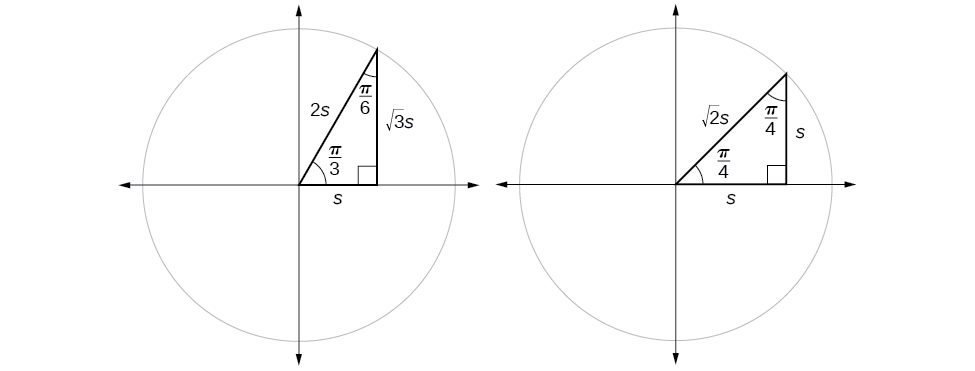
Two side-by-side graphs of circles with inscribed angles. First circle has angle of pi/3 inscribed, radius of 2s, base of length s and height of length . Second circle has angle of pi/4 inscribed with radius , base of length s and height of length s. — Figure \(\PageIndex{8}\): Side lengths of special triangles

We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

Solution

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

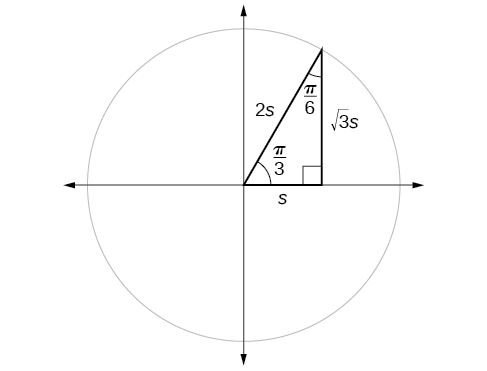
A graph of circle with angle pi/3 inscribed with a radius of 2s, a base with length s and a height of. — Figure \(\PageIndex{9}\): The sine of \(\frac{π}{3}\) equals the cosine of \(\frac{π}{6}\) and vice versa.

This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

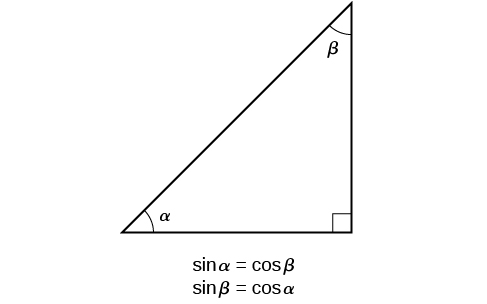
Right triangle with angles alpha and beta. Equivalence between sin alpha and cos beta. Equivalence between sin beta and cos alpha. — Figure \(\PageIndex{10}\): Cofunction identity of sine and cosine of complementary angles

Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\)
\( \cos t= \sin (\frac{π}{2}−t)\)	\( \sin t= \cos (\dfrac{π}{2}−t)\)
\( \tan t= \cot (\dfrac{π}{2}−t) \)	\( \cot t= \tan (\dfrac{π}{2}−t)\)
\( \sec t= \csc (\dfrac{π}{2}−t) \)	\( \csc t= \sec (\dfrac{π}{2}−t)\)

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

To find the sine of the complementary angle, find the cosine of the original angle.
To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

Solution

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Using Right Triangle Trigonometry to Solve Applied Problems

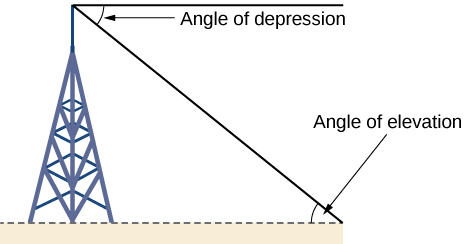
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

Diagram of a radio tower with line segments extending from the top and base of the tower to a point on the ground some distance away. The two lines and the tower form a right triangle. The angle near the top of the tower is the angle of depression. The angle on the ground at a distance from the tower is the angle of elevation. — Figure \(\PageIndex{12}\)

how to: Given a tall object, measure its height indirectly

Make a sketch of the problem situation to keep track of known and unknown information.
Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

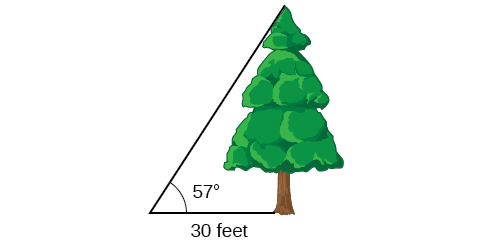
A tree with angle of 57 degrees from vantage point. Vantage point is 30 feet from tree. — Figure \(\PageIndex{13}\)

Solution

We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.