3.5E: Exercises for Section 3.5

Last updated
Save as PDF

Page ID: 71997

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In exercises 1 - 10, find $\dfrac{dy}{dx}$ for the given functions.

1) $y=x^2−\sec x+1$

Answer: $\dfrac{dy}{dx}=2x−\sec x\tan x$

2) $y=3\csc x+\dfrac{5}{x}$

3) $y=x^2\cot x$

Answer: $\dfrac{dy}{dx}=2x\cot x−x^2\csc^2 x$

4) $y=x−x^3\sin x$

5) $y=\dfrac{\sec x}{x}$

Answer: $\dfrac{dy}{dx}=\dfrac{x\sec x\tan x−\sec x}{x^2}$

6) $y=\sin x\tan x$

7) $y=(x+\cos x)(1−\sin x)$

Answer: $\dfrac{dy}{dx}=(1−\sin x)(1−\sin x)−\cos x(x+\cos x)$

8) $y=\dfrac{\tan x}{1−\sec x}$

9) $y=\dfrac{1−\cot x}{1+\cot x}$

Answer: $\dfrac{dy}{dx}=\dfrac{2\csc^2 x}{(1+\cot x)^2}$

10) $y=(\cos x)(1+\csc x)$

In exercises 11 - 16, find the equation of the tangent line to each of the given functions at the indicated values of $x$. Then use a calculator to graph both the function and the tangent line to ensure the equation for the tangent line is correct.

11) [T] $f(x)=−\sin x,\quad x=0$

Answer

$y=−x$

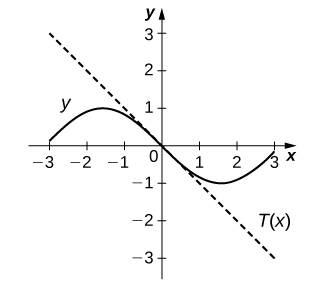
$The graph shows negative sin(x) and the straight line T(x) with slope −1 and y intercept 0.$

12) [T] $f(x)=\csc x,\quad x=\frac{π}{2}$

13) [T] $f(x)=1+\cos x,\quad x=\frac{3π}{2}$

Answer

$y=x+\frac{2−3π}{2}$

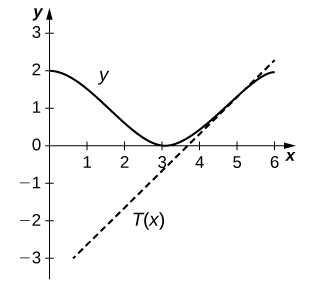
$The graph shows the cosine function shifted up one and has the straight line T(x) with slope 1 and y intercept (2 – 3π)/2.$

14) [T] $f(x)=\sec x,\quad x=\frac{π}{4}$

15) [T] $f(x)=x^2−\tan x, \quad x=0$

Answer

$y=−x$

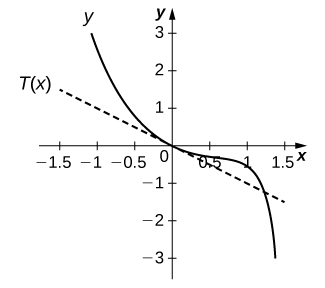
$The graph shows the function as starting at (−1, 3), decreasing to the origin, continuing to slowly decrease to about (1, −0.5), at which point it decreases very quickly.$

16) [T] $f(x)=5\cot x, \quad x=\frac{π}{4}$

In exercises 17 - 22, find $\dfrac{d^2y}{dx^2}$ for the given functions.

17) $y=x\sin x−\cos x$

Answer: $\dfrac{d^2y}{dx^2} = 3\cos x−x\sin x$

18) $y=\sin x\cos x$

19) $y=x−\frac{1}{2}\sin x$

Answer: $\dfrac{d^2y}{dx^2} = \frac{1}{2}\sin x$

20) $y=\dfrac{1}{x}+\tan x$

21) $y=2\csc x$

Answer: $\dfrac{d^2y}{dx^2} = 2\csc(x)\left(\csc^2(x)+\cot^2(x)\right) $

22) $y=\sec^2 x$

23) Find all $x$ values on the graph of $f(x)=−3\sin x\cos x$ where the tangent line is horizontal.

Answer: $x = \dfrac{(2n+1)π}{4}$,where $n$ is an integer

24) Find all $x$ values on the graph of $f(x)=x−2\cos x$ for $0<x<2π$ where the tangent line has slope 2.

25) Let $f(x)=\cot x.$ Determine the points on the graph of $f$ for $0<x<2π$ where the tangent line(s) is (are) parallel to the line $y=−2x$.

Answer: $\left(\frac{π}{4},1\right),\quad \left(\frac{3π}{4},−1\right),\quad\left(\frac{5π}{4},1\right),\quad \left(\frac{7π}{4},−1\right)$

26) [T] A mass on a spring bounces up and down in simple harmonic motion, modeled by the function $s(t)=−6\cos t$ where s is measured in inches and $t$ is measured in seconds. Find the rate at which the spring is oscillating at $t=5$ s.

27) Let the position of a swinging pendulum in simple harmonic motion be given by $s(t)=a\cos t+b\sin t$. Find the constants $a$ and $b$ such that when the velocity is 3 cm/s, $s=0$ and $t=0$.

Answer: $a=0,\quad b=3$

28) After a diver jumps off a diving board, the edge of the board oscillates with position given by $s(t)=−5\cos t$ cm at $t$ seconds after the jump.

a. Sketch one period of the position function for $t≥0$.

b. Find the velocity function.

c. Sketch one period of the velocity function for $t≥0$.

d. Determine the times when the velocity is $0$ over one period.

e. Find the acceleration function.

f. Sketch one period of the acceleration function for $t≥0$.

29) The number of hamburgers sold at a fast-food restaurant in Pasadena, California, is given by $y=10+5\sin x$ where $y$ is the number of hamburgers sold and $x$ represents the number of hours after the restaurant opened at 11 a.m. until 11 p.m., when the store closes. Find $y'$ and determine the intervals where the number of burgers being sold is increasing.

Answer: $y′=5\cos(x)$, increasing on $\left(0,\frac{π}{2}\right),\;\left(\frac{3π}{2},\frac{5π}{2}\right)$, and $\left(\frac{7π}{2},12\right)$

30) [T] The amount of rainfall per month in Phoenix, Arizona, can be approximated by $y(t)=0.5+0.3\cos t$, where $t$ is months since January. Find $y′$and use a calculator to determine the intervals where the amount of rain falling is decreasing.

For exercises 31 - 33, use the quotient rule to derive the given equations.

31) $\dfrac{d}{dx}(\cot x)=−\csc^2x$

32) $\dfrac{d}{dx}(\sec x)=\sec x\tan x$

33) $\dfrac{d}{dx}(\csc x)=−\csc x\cot x$

34) Use the definition of derivative and the identity $\cos(x+h)=\cos x\cos h−\sin x\sin h$ to prove that $\dfrac{d}{dx}(\cos x)=−\sin x$.

For exercises 35 - 39, find the requested higher-order derivative for the given functions.

35) $\dfrac{d^3y}{dx^3}$ of $y=3\cos x$

Answer: $\dfrac{d^3y}{dx^3} = 3\sin x$

36) $\dfrac{d^2y}{dx^2}$ of $y=3\sin x+x^2\cos x$

37) $\dfrac{d^4y}{dx^4}$ of $y=5\cos x$

Answer: $\dfrac{d^4y}{dx^4} = 5\cos x$

38) $\dfrac{d^2y}{dx^2}$ of $y=\sec x+\cot x$

39) $\dfrac{d^3y}{dx^3}$ of $y=x^{10}−\sec x$

Answer: $\dfrac{d^3y}{dx^3} = 720x^7−5\tan(x)\sec^3(x)−\tan^3(x)\sec(x)$

Search

Text Color

Text Size

Margin Size

Font Type