1.3.1: Integers

Last updated
Save as PDF

Page ID: 87250

Leah Griffith, Veronica Holbrook, Johnny Johnson & Nancy Garcia
Rio Hondo College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1.3.1 Learning Objectives

Recognize a real number
Identify particular subsets of the real numbers
Add, subtract, multiply, and divide signed numbers

Real Numbers

Real Number Line
The study of mathematics requires the use of several collections of numbers. The real number line allows us to visually display (graph) the numbers in which we are interested.

A line is composed of infinitely many points. To each point we can associate a unique number, and with each number, we can associate a particular point.

Definition: Real Number

A real number is any number that is the coordinate of a point on the real number line.

Definition: Coordinate

The number associated with a point on the number line is called the coordinate of the point.

Definition: Graph

The point on a number line that is associated with a particular number is called the graph of that number.

Constructing a Real Number Line
We construct a real number line as follows:

Draw a horizontal line.
$A horizontal line with arrows on the end.$
Origin
Choose any point on the line and label it 0. This point is called the origin.
$A horizontal line with arrows on the end. The center has a hash mark labeled 0.$
Choose a convenient length. Starting at 0, mark this length off repeatedly in both directions. When drawing the number line by hand, be careful to have the lengths look like they are the same.
$A horizontal line with arrows on the end. The center has a hash mark labeled 0. There are numerous evenly-spaced hash marks on either side of the zero.$

Definition: Positive Number, Negative Numbers

Real numbers whose graphs are to the right of 0 are called positive real numbers, or more simply, positive numbers. Real numbers whose graphs appear to the left of 0 are called negative real numbers, or more simply, negative numbers.

$A horizontal line with arrows on the end. The center has a hash mark labeled 0. On the right side is a bracket, labeled Positive numbers. On the left side is a bracket, labeled Negative numbers.$

The number 0 is neither positive nor negative.

THE NOTATION OF SIGNED NUMBERS

+ and − Notation
A number is denoted as positive if it is directly preceded by a plus sign or no sign at all.
A number is denoted as negative if it is directly preceded by a minus sign.

Opposites

Opposites
On the number line, each real number, other than zero, has an image on the opposite side of 0. For this reason, we say that each real number has an opposite. Opposites are the same distance from zero but have opposite signs.

The opposite of a real number is denoted by placing a negative sign directly in front of the number. Thus, if $a$ is any real number, then $-a$ is its opposite.

If $a$ is any real number, $-a$ is opposite $a$ on the number line.

$Two number lines. One number line with hash marks from left to right, -a, 0, and a. This number line is titled a positive. A second number line with hash marks from left to right, a, 0, and -a. This number line is titled a negative.$

Reading Signed Numbers

The plus and minus signs now have more than one meaning:

The plus sign can denote the operation of addition or a positive number.

The minus sign can denote the operation of subtraction, a negative number, or the opposite of a number.

To avoid any confusion between "sign" and "operation," it is preferable to read the sign of a number as "positive," "negative," or "opposite of." When "+" is used as an operation sign, it is read as "plus." When "-" is used as an operation sign, it is read as "minus."

Subsets of Real Numbers

The set of real numbers has many subsets. Some of the subsets that are of interest in this course are listed below along with their notations and graphs.

Natural Numbers, Counting Numbers
The natural or counting numbers $(N)$: 1, 2, 3, 4, . . . Read “and so on.”

$A number line containing dots on the hash marks for numbers one through seven.$

Whole Numbers
The whole numbers $(W)$: 0, 1, 2, 3, 4, . . .

$A number line containing dots on the hash marks for numbers zero through seven.$

Notice that every natural number is a whole number.

Integers
The integers $(Z)$: . . . -3, -2, -1, 0, 1, 2, 3, . . .

$A number line containing dots on the hash marks for numbers -4 through 4.$

Notice that every whole number is an integer.

Rational Numbers (Fractions)
The rational numbers $(Q)$: Rational numbers are sometimes called fractions. They are numbers that can be written as the quotient of two integers. They have decimal representations that either terminate or do not terminate but contain a repeating block of digits. Some examples are
$\underbrace{\dfrac{-3}{4} = -0.75}_{text{Terminating}}$ $\underbrace{8 \dfrac{11}{27} = 8.407407407...}_{\text{Nonterminating, but repeating.}}$

Some rational numbers are graphed below.

$A number line containing hash marks for numbers -3 through 4. There are dots for negative three and one-eighths, negative one-half, two-fifths, two divided by one, and three and one-half.$

Notice that every integer is a rational number.

There are still a great many points on the number line that have not yet been assigned a type of number. We will not examine all of these other types of numbers in this text. They are called irrational numbers. An example of these numbers is the number $\pi$, whose decimal representation does not terminate nor contain a repeating block of digits. An approximation for $\pi$ is 3.14.

Absolute Value

Absolute Value-Geometric Approach
Geometric definition of absolute value:
The absolute value of a number $a$, denoted $|a|$, is the distance from a to 0 on the number line.

Absolute value answers the question of "how far," and not "which way." The phrase "how far" implies "length" and length is always a nonnegative quantity. Thus, the absolute value of a number is a nonnegative number.

Example 1

Determine each value.

$|4| = 4$

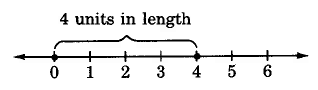
$A number line with hash marks from 0 to 6, with zero to 4 marked as 4 units in length.$

Example 2

$|-4| = 4$

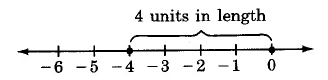
$A number line with hash marks from -6 to 0, with -4 to 0 marked as 4 units in length.$

Example 3

$|0| = 0$

Example 4

$-|5| = -5$. The quantity on the left side of the equal sign is read as "the opposite of the absolute value of 5." The absolute value of 5 is 5. Hence, the opposite of the absolute value of 5 is -5.

Example 5

$-|-3| = -3$. The quantity on the left side of the equal sign is read as "the opposite of the absolute value of -3." The absolute value of -3 is 3. Hence, the opposite of the absolute value of -3 is $-(3) = -3$.

Try It Now 1

By reasoning geometrically, determine the absolute value.

$|7|$

Answer: 7

Addition of Numbers with Like Signs

The addition of the two positive numbers 2 and 3 is performed on the number line as follows.

Begin at 0, the origin.

Since 2 is positive, move 2 units to the right.

Since 3 is positive, move 3 more units to the right.

We are now located at 5.

$A number line with has marks for the numbers -2 to 7. An arrow is drawn from 0 to 2, and from 2 to 5.$

Thus, $2 + 3 = 5$.

Summarizing, we have

$\text{(2 positive units)} + \text{(3 positive units)} = \text{(5 positive units)}$

The addition of the two negative numbers -2 and -3 is performed on the number line as follows.

Begin at 0, the origin.

Since -2 is negative, move 2 units to the left.

Since -3 is negative, move 3 more units to the left.

We are now located at -5.

$A number line with has marks for the numbers -7 to 2. An arrow is drawn from 0 to -2, and from -2 to -5.$

Thus, $(-2) + (-3) = -5$

Summarizing, we have

$\text{(2 negative units)} + \text{(3 negative units)} = \text{(5 negative units)}$

Observing these two examples, we can suggest these relationships:

$\text{(postitive number)} + \text{(positive number)} = \text{(positive number)}$

$\text{(negative number)} + \text{(negative number)} = \text{(negative number)}$

Adding Numbers with the Same Sign
Addition of numbers with like sign:
To add two real numbers that have the same sign, add the absolute values of the numbers and associate with the sum the common sign.

Example 6

Find the sums.

3 + 7

Solution

$\begin{array} {l} {|3| = 3} \\ {|7| = 7} \end{array} \big \}$ Add these absolute values.

3 + 7 = 10

The common sign is “+.”

Thus, $3 + 7 = +10$, or $3 + 7 = 10$.

Example 7

Find the sums.

(-4) + (-9)

Solution

$\begin{array} {l} {|-4| = 4} \\ {|-9| = 9} \end{array} \big \}$ Add these absolute values.

4 + 9 = 13

The common sign is “-.”

Thus, $(-4) + (-9) = -13$.

Addition With Zero

Addition with Zero
Notice that

$(0) + \text{(a positive number)} = \text{(that same positive number)}$.
$(0) + \text{(a negative number)} = \text{(that same negative number)}$.

Definition: The Additive Identity Is Zero

Since adding zero to a real number leaves that number unchanged, zero is called the additive identity.

Addition of Numbers with Unlike Signs

The addition $2 + (-6)$,

two numbers with unlike signs, can also be illustrated using the number line.

Begin at 0, the origin.

Since 2 is positive, move 2 units to the right.

Since -6 is negative, move, from 2, 6 units to the left.

We are now located at -4.

$A number line with has marks for the numbers -5 to 4. An arrow is drawn from 2 to -4, and from 0 to 2.$

We can suggest a rule for adding two numbers that have unlike signs by noting that if the signs are disregarded, 4 can be obtained by subtracting 2 from 6. But 2 and 6 are precisely the absolute values of 2 and -6. Also, notice that the sign of the number with the larger absolute value is negative and that the sign of the resulting sum is negative.

Adding Numbers with Unlike Signs
Addition of numbers with unlike signs: To add two real numbers that have unlike signs, subtract the smaller absolute value from the larger absolute value and associate with this difference the sign of the number with the larger absolute value.

Example 8

Find the following sums.

7 + (-2)

Solution

$\underbrace{|7| = 7}_{\begin{array} {c} {\text{Larger absolute}} \\ {\text{value. Sign is positive.}}\end{array}}$ $\underbrace{|-2| = 2}_{\begin{array} {c} {\text{Larger absolute}} \\ {\text{value. Sign is positive.}}\end{array}}$

Subtract absolute values: 7 - 2 = 5.

Attach the proper sign: "+."

Thus, $7 + (-2) = +5$ or $7 + (-2) = 5$.

Example 9

3 + (-11)

Solution

$\underbrace{|3| = 3}_{\begin{array} {c} {\text{Smaller absolute}} \\ {\text{value}}\end{array}}$ $\underbrace{|-11| = 11}_{\begin{array} {c} {\text{Larger absolute}} \\ {\text{value. Sign is negative.}}\end{array}}$

Subtract absolute values: 11 - 3 = 8.

Attach the proper sign: "-."

Thus, $3 + (-11) = -8$.

Example 10

The morning temperature on a winter's day in Lake Tahoe was -12 degrees. The afternoon temperature was 25 degrees warmer. What was the afternoon temperature?

Solution

We need to find $-12 + 25$.

$\underbrace{|-12| = 12}_{\begin{array} {c} {\text{Smaller absolute}} \\ {\text{value}}\end{array}}$ $\underbrace{|25| = 25}_{\begin{array} {c} {\text{Larger absolute}} \\ {\text{value. Sign is positive.}}\end{array}}$

Subtract absolute values: 25 - 12 = 16.

Attach the proper sign: "+."

Thus, $-12 + 25 = 13$.

Calculators

Calculators having the $A square with a plus and minus sign.$ key can be used for finding sums of signed numbers.

Example 11

Use a calculator to find the sum of -147 and 84.

$\begin{array}{|l|l|l|l|}\hline \\
\hline & & \text{Display Reads} & \\
\hline \text { Type} & 147 & 147 & \\
\hline \text { Press} & +/-& -147 & \text{This key changes the sign of the number, it is different than -.} \\
\hline \text { Press} & +&-147 & \\
\hline \text {Type} & 84 & 84 & \\
\hline \text { Press} & =&-63 \\
\hline
\end{array}$

Definition of Subtraction

We know from experience with arithmetic that the subtraction 5 - 2 produces 3, that is 5 - 2 = 3. We can suggest a rule for subtracting signed numbers by illustrating this process on the number line.

$A number line with hash marks from -1 to 7. There is an arrow from 0 to 5 and from 5 to 3.$

Begin at 0, the origin.

Since 5 is positive, move 5 units to the right.

Then, move 2 units to the left to get to 6. (This reminds us of addition with a negative number.)

From this illustration we can see that 5 - 2 is the same as 5 + (-2). This leads us directly to the definition of subtraction.

Definition of Subtraction
If $a$ and $b$ are real numbers, $a - b$ is the same as $a + (-b)$, where $-b$ is the opposite of $b$.

The Process of Subtraction

From this definition, we suggest the following rule for subtracting signed numbers.

Subtraction of Signed Numbers
To perform the subtraction $a - b$, add the opposite of $b$ to $a$, that is, change the sign of $b$ and add.

Example 12

Perform the indicated subtractions.

5 - 3 = 5 + (-3) = 2
4 - 9 = 4 + (-9) = -5
-4 - 6 = -4 + (-6) = -10
-3 - (-12) = -3 + 12 = 9

Example 13

The high temperature today in Lake Tahoe was 26°F. The low temperature tonight is expected to be -7°F. How many degrees is the temperature expected to drop?

Solution

We need to find the difference between 26 and -7.

26 - (-7) = 26 + 7 = 33

Thus, the expected temperature drop is 33°F.

Example 14

$\begin{array} {rcl} {-6 - (-5) - 10} & = & {-6 + 5 + (-10)} \\ {} & = & {(-6 + 5) + (-10)} \\ {} & = & {-1 + (-10)} \\ {} & = & {-11} \end{array}$

Try It Now 2

Perform the indicated subtractions.

9 − 6

Answer: 3

Calculators

Calculators can be used for subtraction of signed numbers. The most efficient calculators are those with a $A box with a plus and minus sign.$ key.

Example 15

Use a calculator to find the difference.

-156 - (-211)

Solution

$\begin{array}{|l|l|l|}\hline \\
\hline & & \text{Display Reads}   \\
\hline \text { Type} & 156 & 156 \\
\hline \text { Press} &  +/-& -156 \\
\hline \text { Type} &   -& -156 \\
\hline \text { Press} & 211& 211 \\
\hline \text {Type} & +/- & -211 \\
\hline \text { Press} & =&-55 \\
\hline
\end{array}$

Multiplication of Signed Numbers

Let us consider first, the product of two positive numbers. Multiply: $3 \cdot 5$.

$3 \cdot 5$ means $5 + 5 + 5 = 15$

This suggests that

$\text{(positive number)} \cdot \text{(positive number)} = \text{(positive number)}$

More briefly,

(+) (+) = (+)

Now consider the product of a positive number and a negative number. Multiply: (3)(-5)

(3)(-5) means (-5) + (-5) + (-5) = -15

This suggests that

$\text{(positive number)} \cdot \text{(negative number)} = \text{(negative number)}$

More briefly,

(+) (-) = (-)

By the commutative property of multiplication, we get

$\text{(negative number)} \cdot \text{(positive number)} = \text{(negative number)}$

More briefly,

(-) (+) = (-)

The sign of the product of two negative numbers can be suggested after observing the following illustration.

Multiply -2 by, respectively, 4, 3, 2, 1, 0, -1, -2, -3, -4.

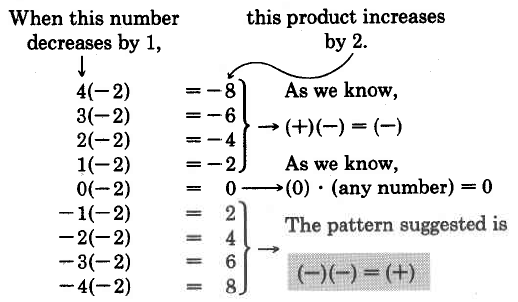
$A list of equations. 4 times negative 2 equals negative 8. 3 times negative 2 equals negative 6. 2 times negative 2 equals negative 4. 1 times negative 2 equals negative 2. For all this, the following label is listed on the side: As we know, a negative times a positive equals a negative. The list continues. 0 times negative 2 equals 0. The following label is listed to the side: As we know, 0 times any number equals 0. The list continues further. Negative 1 times negative 2 equals 2. Negative 2 times negative 2 equals 4. Negative 3 times negative 2 equals 6. Negative 4 times negative 2 equals 8. The following label is listed to the side: The pattern suggested is a negative times a negative equals a positive. For the entire list, the label at the top says: when this number decreases by 1, the first factor in each multiplication problem, the product increases by 2.$

We have the following rules for multiplying signed numbers.

Rules for Multiplying Signed Numbers
Multiplying signed numbers:

To multiply two real numbers that have the same sign, multiply their absolute values. The product is positive.
(+) (+) = (+)
(-) (-) = (+)
To multiply two real numbers that have opposite signs, multiply their absolute values. The product is negative.
(+) (-) = (-)
(-) (+) = (-)

Example 16

Find the following products.

$8 \cdot 6$

Solution

$\begin{array} {ccl} {|8|} & = & {8} \\ {|6|} & = & {6} \end{array} \big \}$ Multiply these absolute values.

$8 \cdot 6 = 48$

Since the numbers have the same sign, the product is positive.

Thus, $8 \cdot 6 = +48$, or $8 \cdot 6 = 48$.

Example 17

(-8)(-6)

Solution

$\begin{array} {ccl} {|-8|} & = & {8} \\ {|-6|} & = & {6} \end{array} \big \}$ Multiply these absolute values.

$8 \cdot 6 = 48$

Since the numbers have the same sign, the product is positive.

Thus, $(-8)(-6) = +48$, or $(-8)(-6) = 48$.

Example 18

(-4)(7)

Solution

$\begin{array} {ccl} {|-4|} & = & {4} \\ {|7|} & = & {7} \end{array} \big \}$ Multiply these absolute values.

$4 \cdot 7 = 28$

Since the numbers have opposite signs, the product is negative.

Thus, (-4)(7) = -28.

Example 19

6(-3)

Solution

$\begin{array} {ccl} {|6|} & = & {6} \\ {|-3|} & = & {3} \end{array} \big \}$ Multiply these absolute values.

$6 \cdot 3 = 18$

Since the numbers have opposite signs, the product is negative.

Thus, 6(-3) = -18.

Division of Signed Numbers

To determine the signs in a division problem, recall that

$\dfrac{12}{3} = 4$ since $12 = 3 \cdot 4$

This suggests that

$\dfrac{(+)}{(+)} = (+)$

$\dfrac{(+)}{(+)} = (+)$ since (+) = (+) (+)

What is $\dfrac{12}{-3}$?

12 = (-3)(-4) suggests that $\dfrac{12}{-3} = -4$. That is,

$\dfrac{(+)}{(-)} = (-)$

(+) = (-) (-) suggests that $\dfrac{(+)}{(-)} = (-)$

What is $\dfrac{-12}{3}$?

-12 = (3)(-4) suggests that $\dfrac{-12}{3} = -4$. That is,

$\dfrac{(-)}{(+)} = (-)$

(-) = (+) (-) suggests that $\dfrac{(-)}{(+)} = (-)$

What is $\dfrac{-12}{-3}$?

-12 = (-3)(4) suggests that $\dfrac{-12}{-3} = 4$. That is,

$\dfrac{(-)}{(-)} = (+)$

(-) = (-)(+) suggests that $\dfrac{(-)}{(-)} = (+)$

We have the following rules for dividing signed numbers.

Rules for Dividing Signed Numbers
Dividing signed numbers:

To divide two real numbers that have the same sign, divide their absolute values. The quotient is positive.
$\dfrac{(+)}{(+)} = (+)\dfrac{(-)}{(-)} = (+)$
To divide two real numbers that have opposite signs, divide their absolute values. The quotient is negative.
$\dfrac{(-)}{(+)} = (-)\dfrac{(+)}{(-)} = (-)$

Example 20

Find the following quotients.

$\dfrac{-10}{2}$

Solution

$\begin{array} {ccc} {|-10|} & = & {10} \\ {|2|} & = & {2} \end{array} \big \}$ Divide these absolute values.

$\dfrac{10}{2} = 5$

Since the numbers have opposite signs, the quotient is negative.

Thus $\dfrac{-10}{2} = -5$.

Example 21

$\dfrac{-35}{-7}$

Solution

$\begin{array} {ccc} {|-35|} & = & {35} \\ {|-7|} & = & {7} \end{array} \big \}$ Divide these absolute values.

$\dfrac{35}{7} = 5$

Since the numbers have the same signs, the quotient is positive.

Thus $\dfrac{-35}{-7} = 5$.

Example 22

$\dfrac{18}{-9}$

Solution

$\begin{array} {ccc} {|18|} & = & {18} \\ {|-9|} & = & {9} \end{array} \big \}$ Divide these absolute values.

$\dfrac{18}{9} = 2$

Since the numbers have opposite signs, the quotient is negative.

Thus $\dfrac{18}{-9} = -2$.

Calculators

Calculators with the $A box with a plus and minus sign.$ key can be used for multiplying and dividing signed numbers.

Example 23

Use a calculator to find each quotient or product.

$(-186) \cdot (-43)$

Solution

Since this product involves a $\text{(negative)} \cdot \text{(negative)}$, we know the result should be a positive number. We'll illustrate this on the calculator.

$\begin{array}{|l|l|l|}\hline \\
\hline & & \text{Display Reads}   \\
\hline \text { Type} & 186 & 186 \\
\hline \text { Press} &  +/-& -186 \\
\hline \text { Press} &   \times & -186 \\
\hline \text { Type} & 43& 43 \\
\hline \text {Press} & +/- & -43 \\
\hline \text { Press} & =& 7998 \\
\hline
\end{array}$

Thus, $(-186) \cdot (-43) = 7,998$

Example 24

$\dfrac{158.64}{-54.3}$. Round to one decimal place.

Solution

Since this product involves a $\text{(negative)} \cdot \text{(negative)}$, we know the result should be a positive number. We'll illustrate this on the calculator.

$\begin{array}{|l|l|l|}\hline \\
\hline & & \text{Display Reads} \\
\hline \text { Type} & 158.64 & 158.64 \\
\hline \text { Press} & \div & 158.64 \\
\hline \text { Type} & 54.3& 54.3 \\
\hline \text { Press} & +/-& -54.3 \\
\hline \text { Press} & =& -2.921546961 \\
\hline
\end{array}$

Rounding to one decimal place we get -2.9.

Search

Text Color

Text Size

Margin Size

Font Type