6.1.5: Simplification of Denominate Numbers

Last updated
Save as PDF

Page ID: 87300

Leah Griffith, Veronica Holbrook, Johnny Johnson & Nancy Garcia
Rio Hondo College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

6.1.5 Learning Objectives

Convert an unsimplified unit of measure to a simplified unit of measure
Perform arithmetic calculations with denominate numbers

Converting to Multiple Units

Definition: Denominate Numbers

Numbers that have units of measure associated with them are called denominate numbers. It is often convenient, or even necessary, to simplify a denominate number.

Definition: Simplified Denominate Numbers

A denominate number is simplified when the number of standard units of measure associated with it does not exceed the next higher type of unit.

The denominate number 55 min is simplified since it is smaller than the next higher type of unit, 1 hr. The denominate number 65 min is not simplified since it is not smaller than the next higher type of unit, 1 hr. The denominate number 65 min can be simplified to 1 hr 5 min. The denominate number 1 hr 5 min is simplified since the next higher type of unit is day, and 1 hr does not exceed 1 day.

Example 1

Simplify 19 in.

Solution

Since $\text{12 in = 1 ft.}$, and $19 = 12 + 7$,

$\begin{array} {rcl} {\text{19 in}} & = & {\text{12 in + 7 in}} \\ {} & = & {\text{1 ft + 7 in}} \\ {} & = & {\text{1 ft 7 in}} \end{array}$

Example 2

Simplify 4 gal 5 qt.

Solution

Since $\text{4 qt = 1 gal}$, and $5 = 4 + 1$,

$\begin{array} {rcl} {\text{4 gal 5 qt}} & = & {\text{4 gal + 4 qt + 1 qt}} \\ {} & = & {\text{4 gal + 1 gal + 1 qt}} \\ {} & = & {\text{5 gal + 1 qt}} \\ {} & = & {\text{5 gal 1 qt}}\end{array}$

Example 3

Simplify 2 hr 75 min.

Solution

Since $\text{60 min = 1 hr}$, and $75 = 60 + 15$,

$\begin{array} {rcl} {\text{2 hr 75 min}} & = & {\text{2 hr + 60 min + 15 min}} \\ {} & = & {\text{2 hr + 1 hr + 15 min}} \\ {} & = & {\text{3 hr + 15 min}} \\ {} & = & {\text{3 hr 15 min}}\end{array}$

Example 4

Simplify 43 fl oz.

Solution

Since $\text{8 fl oz = 1 c}$ (1 cup), and $43 \div 8 = \text{5R3}$,

$\begin{array} {rcl} {\text{43 fl oz}} & = & {\text{40 fl oz + 3 fl oz}} \\ {} & = & {5 \cdot 8 \text{ fl oz + 3 fl oz}} \\ {} & = & {5 \cdot 1 \text{ c + 3 fl oz}} \\ {} & = & {\text{5 c + 3 fl oz}}\end{array}$

But, $\text{2c = 1 pt}$ and $5 \div 2 = \text{2R1}$. So,

$\begin{array} {rcl} {\text{5 c + 3 fl oz}} & = & {2 \cdot 2 \text{ c + 1 c + 3 fl oz}} \\ {} & = & {2 \cdot 1 \text{ pt + 1 c + 3 fl oz}} \\ {} & = & {\text{2 pt + 1 c + 3 fl oz}} \end{array}$

But, $\text{2 pt = 1 qt}$, so

$\text{2 pt + 1 c + 3 fl oz = 1 qt 1 c 3 fl oz}$

Try It Now 1

Simplify each denominate number. Refer to the conversion tables given in [link], if necessary.

18 in
8 gal 9 qt
5 hr 80 min
8 wk 11 days
86 days

Answer

1 ft 6 in
10 gal 1 qt
6 hr 20 min
9 wk 4 days
12 wk 2 days

Adding and Subtracting Denominate Numbers

Adding and Subtracting Denominate Numbers
Denominate numbers can be added or subtracted by:

writing the numbers vertically so that the like units appear in the same column.
adding or subtracting the number parts, carrying along the unit.
simplifying the sum or difference.

Example 5

Add 6 ft 8 in to 2 ft 9 in.

Solution

$\begin{array} {r} {\text{6 ft 8 in}} \\ {\underline{\text{+ 2 ft 9 in}}} \\ {\text{8 ft 17 in}} \end{array}$ Simplify this denominate number.

Since $\text{12 in = 1 ft}$,

$\begin{array} {rcl} {\text{8 ft + 12 in + 5 in}} & = & {\text{8 ft + 1 ft + 5 in}} \\ {} & = & {\text{9 ft + 5 in}} \\ {} & = & {\text{9 ft 5 in}} \end{array}$

Example 6

Subtract 5 da 3 hr from 8 da 11 hr.

Solution

$\begin{array} {r} {\text{8 da 11 hr}} \\ {\underline{\text{- 5 da 3 hr}}} \\ {\text{3 da 8 hr}} \end{array}$

Example 7

Subtract 3 lb 14 oz from 5 lb 3 oz.

Solution

$\begin{array} {r} {\text{5 lb 3 oz}} \\ {\underline{\text{- 3 lb 14 oz}}} \end{array}$

We cannot directly subtract 14 oz from 3 oz, so we must borrow 16 oz from the pounds.

$\begin{array} {rcl} {\text{5 lb 3 oz}} & = & {\text{5 lb + 3 oz}} \\ {} & = & {\text{4 lb + 1 lb + 3 oz}} \\ {} & = & {\text{4 lb + 16 oz + 3 oz (Since 1 lb = 16 oz)}} \\ {} & = & {\text{4 lb + 19 oz}} \\ {} & = & {\text{4 lb 19 oz}} \end{array}$

$\begin{array} {r} {\text{4 lb 19 oz}} \\ {\underline{\text{- 3 lb 14 oz}}} \\ {\text{1 lb 5 oz}} \end{array}$

Example 8

Subtract 4 da 9 hr 21 min from 7 da 10 min.

Solution

$\begin{array} {r} {\text{7 da 0 hr 10 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \end{array}$ Borrow 1 da from the 7 da.

$\begin{array} {r} {\text{6 da 24 hr 10 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \end{array}$ Borrow 1 hr from the 24 hr.

$\begin{array} {r} {\text{6 da 23 hr 70 min}} \\ {\underline{\text{- 4 da 9 hr 21 min}}} \\ {\text{2 da 14 hr 49 min}} \end{array}$

Try It Now 2

Perform each operation. Simplify when possible.

Add 4 gal 3 qt to 1 gal 2 qt.
Add 9 hr 48 min to 4 hr 26 min.
Subtract 2 ft 5 in from 8 ft 7 in.
Subtract 15 km 460 m from 27 km 800 m.
Subtract 8 min 35 sec from 12 min 10 sec.

Answer

6 gal 1 qt
14 hr 14 min
6 ft 2in
12 km 340 m
3 min 35 sec

Multiplying a Denominate Number by a Whole Number

Let's examine the repeated sum

$\underbrace{\text{4 ft 9 in + 4 ft 9 in + 4 ft 9 in}}_{\text{3 times}} = \text{12 ft 27 in}$

Recalling that multiplication is a description of repeated addition, by the distributive property we have

$\begin{array} {rcl} {\text{3(4 ft 9 in)}} & = & {\text{3 (4ft + 9 in)}} \\ {} & = & {3 \cdot 4 \text{ ft } + 3 \cdot 9 \text{ in}} \\ {} & = & {\text{12 ft + 27 in. Now, 27 in = 2 ft 3 in}} \\ {} & = & {\text{12 ft + 2 ft + 3 in}} \\ {} & = & {\text{14 ft + 3 in}} \\ {} & = & {\text{14 ft 3 in}} \end{array}$

From these observations, we can suggest the following rule.

Multiplying a Denominate Number by a Whole Number
To multiply a denominate number by a whole number, multiply the number part of each unit by the whole number and affix the unit to this product.

Example 9

Perform the following multiplications. Simplify if necessary.

$\begin{array} {rcl} {6 \cdot \text{(2 ft 4 in)}} & = & {6 \cdot 2 \text{ ft + 6} \cdot 4 \text{in}} \\ {} & = & {\text{12 ft + 24 in}} \end{array}$

Since $\text{3 ft = 1 yd}$ and $\text{12 in = 1 ft}$,

$\begin{array} {rcl} {\text{12 ft + 24 in}} & = & {\text{4 yd + 2 ft}} \\ {} & = & {\text{4 yd 2 ft}} \end{array}$

Example 10

$\begin{array} {rcl} {8 \cdot \text{(5 hr 21 min 55 sec)}} & = & {8 \cdot 5 \text{ hr} + 8 \cdot 21 \text{ min} + 8 \cdot 55 \text{ sec}} \\ {} & = & {\text{40 hr + 168 min + 440 sec}} \\ {} & = & {\text{40 hr + 168 min + 7 min + 20 sec}} \\ {} & = & {\text{40 hr + 175 min + 20 sec}} \\ {} & = & {\text{40 hr + 2 hr + 55 min + 20 sec}} \\ {} & = & {\text{42 hr + 55 min + 20 sec}} \\ {} & = & {\text{24 hr + 18 hr + 55 min + 20 sec}} \\ {} & = & {\text{1 da + 18 hr + 55 min + 20 sec}} \\ {} & = & {\text{1 da 18 hr 55 min 20 sec}} \end{array}$

Try It Now 3

Perform the following multiplications. Simplify.

$2 \cdot \text{(10 min)}$
$5 \cdot \text{(3 qt)}$
$4 \cdot \text{(5 ft 8 in)}$

Answer

20 min
$\text{15 qt = 3 gal 3 qt}$
$\text{20 ft 32 in = 7 yd 1 ft 8 in}$

Dividing a Denominate Number by a Whole Number

Dividing a Denominate Number by a Whole Number
To divide a denominate number by a whole number, divide the number part of each unit by the whole number beginning with the largest unit. Affix the unit to this quotient. Carry any remainder to the next unit.

Example 11

Perform the following divisions. Simplify if necessary.

$\text{(12 min 40 sec)} \div 4$

Solution

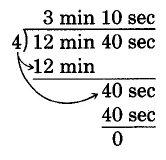
$Long division. 12 min and 40 sec divided by 4. 4 goes into 12 minutes 3 times, making a quotient of 3 minutes with no remainder. 4 goes into 40 seconds 10 times, making a quotient of 10 seconds with no remainder. The total quotient is 3 min 10 sec.$

Thus $\text{(12 min 40 sec)} \div 4 = \text{3 min 10 sec}$.

Example 12

$\text{(5 yd 2 ft 9 in)} \div 3$

Solution

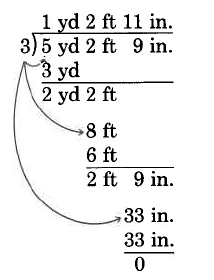
$Long division. 5 yd 2 ft 9 in divided by 3. 3 goes into 5 yards one time with a remainder of 2 yards. Bring down the 2 feet. 2 yards and 2 feet is eight feet. 3 goes into eight feet twice with a remainder of 2 feet. Bring down the 9 inches. 2 feet 9 in is equal to 22 inches. 3 goes into 33 inches exactly 11 times. The total quotient is 1 yd 2 ft 11 in.$

$\begin{array} {c} {\text{Convert to feet: 2 yd 2 ft = 8 ft}} \\ {\text{Convert to inches: 2 ft 9 in. = 33 in}} \end{array}$

Thus $\text{(5 yd 2 ft 9 in)} \div 3 = \text{1 yd 2 ft 11 in}$.

Try It Now 4

Perform the following divisions. Simplify if necessary.

$\text{(18 hr 36 min)} \div 9$
$\text{(36 hr 8 min)} \div 8$
$\text{(13 yd 7 in)} \div 5$

Answer

2 hr 4 min
4 hr 18 min
2 yd 1 ft 11 in

Search

Text Color

Text Size

Margin Size

Font Type