6.10.2: Kernel and Image of a Linear Transformation

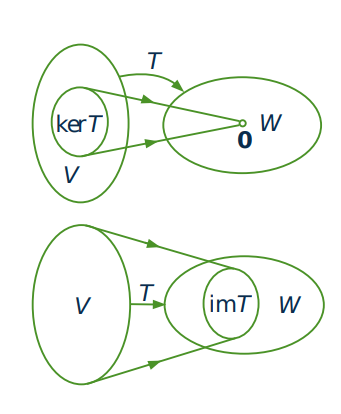
This section is devoted to two important subspaces associated with a linear transformation \(T : V \to W\).

Definition: \(\PageIndex{1}\)Kernel and Image of a Linear Transformation

The kernel of \(T\) (denoted \(\text{ker }T\)) and the image of \(T\) (denoted \(im \; T\) or \(T(V)\)) are defined by

\[\begin{aligned} \text{ker }T &= \{\mathbf{v} \mbox{ in } V \mid T(\mathbf{v}) = \mathbf{0}\} \\ im \;T &= \{T(\mathbf{v}) \mid \mathbf{v} \mbox{ in } V\} = T(V)\end{aligned} \nonumber \]

The kernel of \(T\) is often called the nullspace of \(T\) because it consists of all vectors \(\mathbf{v}\) in \(V\) satisfying the condition that \(T(\mathbf{v}) = \mathbf{0}\). The image of \(T\) is often called the range of \(T\) and consists of all vectors \(\mathbf{w}\) in \(W\) of the form \(\mathbf{w} = T(\mathbf{v})\) for some \(\mathbf{v}\) in \(V\). These subspaces are depicted in the diagrams.

Example \(\PageIndex{1}\)

Let \(T_{A} : \mathbb{R}^n \to \mathbb{R}^m\) be the linear transformation induced by the \(m \times n\) matrix \(A\), that is \(T_{A}(\mathbf{x}) = A\mathbf{x}\) for all columns \(\mathbf{x}\) in \(\mathbb{R}^n\). Then

\[\begin{aligned} &\text{ker }T_{A} = \{\mathbf{x} \mid A\mathbf{x} = \mathbf{0}\} = null \;A \quad \mbox{ and } \\ &im \;T_{A} = \{A\mathbf{x} \mid \mathbf{x} \mbox{ in } \mathbb{R}^n\} = im \;A\end{aligned} \nonumber \]

Hence the following theorem extends Example [exa:013498].

Theorem \(\PageIndex{1}\)

Let \(T : V \to W\) be a linear transformation.

1. \(\text{ker }T\) is a subspace of \(V\).
2. \(im \;T\) is a subspace of \(W\).

Proof. The fact that \(T(\mathbf{0}) = \mathbf{0}\) shows that \(\text{ker }T\) and \(im \;T\) contain the zero vector of \(V\) and \(W\) respectively.

1. If \(\mathbf{v}\) and \(\mathbf{v}_{1}\) lie in \(\text{ker }T\), then \(T(\mathbf{v}) = \mathbf{0} = T(\mathbf{v}_{1})\), so

   \[\begin{aligned} T(\mathbf{v} + \mathbf{v}_1) &= T(\mathbf{v}) + T(\mathbf{v}_1) = \mathbf{0} + \mathbf{0} = \mathbf{0} \\ T(r\mathbf{v}) &= rT(\mathbf{v}) = r\mathbf{0} = \mathbf{0} \quad \mbox{ for all } r \mbox{ in } \mathbb{R}\end{aligned} \nonumber \]

2. If \(\mathbf{w}\) and \(\mathbf{w}_{1}\) lie in \(im \;T\), write \(\mathbf{w} = T(\mathbf{v})\) and \(\mathbf{w}_{1} = T(\mathbf{v}_{1})\) where \(\mathbf{v}, \mathbf{v}_{1} \in V\). Then

   \[\begin{aligned} \mathbf{w} + \mathbf{w}_1 &= T(\mathbf{v}) + T(\mathbf{v}_1) = T(\mathbf{v} + \mathbf{v}_1) \\ r\mathbf{w} &= rT(\mathbf{v}) = T(r\mathbf{v}) \quad \mbox{ for all } r \mbox{ in } \mathbb{R}\end{aligned} \nonumber \]

Given a linear transformation \(T : V \to W\):

\(dim \;(\text{ker }T)\) is called the \(\textbf{nullity}\) of \(T\) and denoted as \(nullity \;(T)\)

\(dim \;(im \;T)\) is called the \(\textbf{rank}\) of \(T\) and denoted as \(rank \;(T)\)

The \(rank \;\) of a matrix \(A\) was defined earlier to be the dimension of \(col \;A\), the column space of \(A\). The two usages of the word \(\textit{rank}\) are consistent in the following sense. Recall the definition of \(T_{A}\) in Example \(\PageIndex{1}\).

Example \(\PageIndex{2}\)

Given an \(m \times n\) matrix \(A\), show that \(im \;T_{A} = col \; A\), so \(rank \;T_{A} = rank \;A\).

Solution

Write \(A = \left[ \begin{array}{ccc} \mathbf{c}_{1} & \cdots & \mathbf{c}_{n} \end{array} \right]\) in terms of its columns. Then

\[im \;T_{A} = \{A\mathbf{x} \mid \mathbf{x} \mbox{ in } \mathbb{R}^n\} = \{x_1\mathbf{c}_1 + \cdots + x_n\mathbf{c}_n \mid x_i \mbox{ in } \mathbb{R} \} \nonumber \]

using Definition 2.5. Hence \(im \;T_{A}\) is the column space of \(A\); the rest follows.

Often, a useful way to study a subspace of a vector space is to exhibit it as the kernel or image of a linear transformation. Here is an example.

Example \(\PageIndex{3}\)

Define a transformation \(P :\|{M}_{nn} \to\|{M}_{nn}\) by \(P(A) = A - A^{T}\) for all \(A\) in \(\textbf{M}_{nn}\). Show that \(P\) is linear and that:

1. \(\text{ker }P\) consists of all symmetric matrices.
2. \(im \;P\) consists of all skew-symmetric matrices.

Solution

The verification that \(P\) is linear is left to the reader. To prove part (a), note that a matrix \(A\) lies in \(\text{ker }P\) just when \(0 = P(A) = A - A^{T}\), and this occurs if and only if \(A = A^{T}\)—that is, \(A\) is symmetric. Turning to part (b), the space \(im \;P\) consists of all matrices \(P(A)\), \(A\) in \(\textbf{M}_{nn}\). Every such matrix is skew-symmetric because

\[P(A)^T = (A - A^T)^T = A^T - A = -P(A) \nonumber \]

On the other hand, if \(S\) is skew-symmetric (that is, \(S^{T} = -S\)), then \(S\) lies in \(im \;P\). In fact,

\[P\left[ \frac{1}{2}S\right] = \frac{1}{2}S - \left[ \frac{1}{2}S\right]^T = \frac{1}{2}(S - S^T) = \frac{1}{2}(S + S) = S \nonumber \]

One-to-One and Onto Transformations

Definition: \(\PageIndex{2}\)One-to-one and Onto Linear Transformations

Let \(T : V \to W\) be a linear transformation.

1. \(T\) is said to be onto if \(im \;T = W\).
2. \(T\) is said to be one-to-one if \(T(\mathbf{v}) = T(\mathbf{v}_{1})\) implies \(\mathbf{v} = \mathbf{v}_{1}\).

A vector \(\mathbf{w}\) in \(W\) is said to be hit by \(T\) if \(\mathbf{w} = T(\mathbf{v})\) for some \(\mathbf{v}\) in \(V\). Then \(T\) is onto if every vector in \(W\) is hit at least once, and \(T\) is one-to-one if no element of \(W\) gets hit twice. Clearly the onto transformations \(T\) are those for which \(im \;T = W\) is as large a subspace of \(W\) as possible. By contrast, Theorem \(\PageIndex{2}\) shows that the one-to-one transformations \(T\) are the ones with \(\text{ker }T\) as small a subspace of \(V\) as possible.

Theorem \(\PageIndex{2}\)

If \(T : V \to W\) is a linear transformation, then \(T\) is one-to-one if and only if \(\text{ker }T = \{\mathbf{0}\}\).

Proof: If \(T\) is one-to-one, let \(\mathbf{v}\) be any vector in \(\text{ker }T\). Then \(T(\mathbf{v}) = \mathbf{0}\), so \(T(\mathbf{v}) = T(\mathbf{0})\). Hence \(\mathbf{v} = \mathbf{0}\) because \(T\) is one-to-one. Hence \(\text{ker }T = \{\mathbf{0}\}\).

Conversely, assume that \(\text{ker }T = \{\mathbf{0}\}\) and let \(T(\mathbf{v}) = T(\mathbf{v}_{1})\) with \(\mathbf{v}\) and \(\mathbf{v}_{1}\) in \(V\). Then \(T(\mathbf{v} - \mathbf{v}_{1}) = T(\mathbf{v}) - T(\mathbf{v}_{1}) = \mathbf{0}\), so \(\mathbf{v} - \mathbf{v}_{1}\) lies in \(\text{ker }T = \{\mathbf{0}\}\). This means that \(\mathbf{v} - \mathbf{v}_{1} = \mathbf{0}\), so \(\mathbf{v} = \mathbf{v}_{1}\), proving that \(T\) is one-to-one.

Example \(\PageIndex{4}\)

The identity transformation \(1_{V} : V \to V\) is both one-to-one and onto for any vector space \(V\).

Example \(\PageIndex{5}\)

Consider the linear transformations

\[\begin{aligned} S& : \mathbb{R}^3 \to \mathbb{R}^2 \quad \mbox{given by } S(x, y, z) = (x + y, x - y) \\ T& : \mathbb{R}^2 \to \mathbb{R}^3 \quad \mbox{given by } T(x, y) = (x + y, x - y, x) \end{aligned} \nonumber \]

Show that \(T\) is one-to-one but not onto, whereas \(S\) is onto but not one-to-one.

Solution

The verification that they are linear is omitted. \(T\) is one-to-one because

\[\text{ker }T = \{(x, y) \mid x + y = x - y = x = 0\} = \{(0, 0)\} \nonumber \]

However, it is not onto. For example \((0, 0, 1)\) does not lie in \(im \;T\) because if \((0, 0, 1) = (x + y, x - y, x)\) for some \(x\) and \(y\), then \(x + y = 0 = x - y\) and \(x = 1\), an impossibility. Turning to \(S\), it is not one-to-one by Theorem [thm:021411] because \((0, 0, 1)\) lies in \(\text{ker }S\). But every element \((s, t)\) in \(\mathbb{R}^2\) lies in \(im \;S\) because \((s, t) = (x + y, x - y) = S(x, y, z)\) for some \(x\), \(y\), and \(z\) (in fact, \(x = \frac{1}{2}(s + t)\), \(y = \frac{1}{2}(s - t)\), and \(z = 0\)). Hence \(S\) is onto.

Example \(\PageIndex{6}\)

Let \(U\) be an invertible \(m \times m\) matrix and define

\[T :\|{M}_{mn} \to\|{M}_{mn} \quad \mbox{by} \quad T(X) = UX \mbox{ for all } X \mbox{ in }\|{M}_{mn} \nonumber \]

Show that \(T\) is a linear transformation that is both one-to-one and onto.

Solution

The verification that \(T\) is linear is left to the reader. To see that \(T\) is one-to-one, let \(T(X) = 0\). Then \(UX = 0\), so left-multiplication by \(U^{-1}\) gives \(X = 0\). Hence \(\text{ker }T = \{\mathbf{0}\}\), so \(T\) is one-to-one. Finally, if \(Y\) is any member of \(\textbf{M}_{mn}\), then \(U^{-1}Y\) lies in \(\textbf{M}_{mn}\) too, and \(T(U^{-1}Y) = U(U^{-1}Y) = Y\). This shows that \(T\) is onto.

The linear transformations \(\mathbb{R}^n \to \mathbb{R}^m\) all have the form \(T_{A}\) for some \(m \times n\) matrix \(A\) (Theorem [thm:005789]). The next theorem gives conditions under which they are onto or one-to-one. Note the connection with Theorem [thm:015672] and Theorem [thm:015711].

Theorem \(\PageIndex{3}\)

Let \(A\) be an \(m \times n\) matrix, and let \(T_{A} : \mathbb{R}^n \to \mathbb{R}^m\) be the linear transformation induced by \(A\), that is \(T_{A}(\mathbf{x}) = A\mathbf{x}\) for all columns \(\mathbf{x}\) in \(\mathbb{R}^n\).

1. \(T_{A}\) is onto if and only if \(rank \;A = m\).
2. \(T_{A}\) is one-to-one if and only if \(rank \;A = n\).

Proof.

1. We have that \(im \;T_{A}\) is the column space of \(A\) (see Example [exa:021363]), so \(T_{A}\) is onto if and only if the column space of \(A\) is \(\mathbb{R}^m\). Because the \(rank \;\) of \(A\) is the dimension of the column space, this holds if and only if \(rank \;A = m\).
2. \(\text{ker }T_{A} = \{\mathbf{x} \mbox{ in } \mathbb{R}^n \mid A\mathbf{x} = \mathbf{0}\}\), so (using Theorem [thm:021411]) \(T_{A}\) is one-to-one if and only if \(A\mathbf{x} = \mathbf{0}\) implies \(\mathbf{x} = \mathbf{0}\). This is equivalent to \(rank \;A = n\) by Theorem [thm:015672].

The Dimension Theorem

Let \(A\) denote an \(m \times n\) matrix of \(rank \;r\) and let \(T_{A} : \mathbb{R}^n \to \mathbb{R}^m\) denote the corresponding matrix transformation given by \(T_{A}(\mathbf{x}) = A\mathbf{x}\) for all columns \(\mathbf{x}\) in \(\mathbb{R}^n\). It follows from Example [exa:021319] and Example [exa:021363] that \(im \;T_{A} = col \; A\), so \(dim \;(im \;T_{A}) =dim \; col \; A) = r\). On the other hand Theorem [thm:015561] shows that \(dim \;(\text{ker }T_{A}) =dim \;(null \;A) = n - r\). Combining these we see that

\[dim \;(im \; T_A) +dim \;(\text{ker }T_A) = n \quad \mbox{for every } m \times n \mbox{ matrix } A \nonumber \]

The main result of this section is a deep generalization of this observation.

Theorem \(\PageIndex{4}\) DimensionTheorem

Let \(T : V \to W\) be any linear transormation and assume that \(\text{ker }T\) and \(im \;T\) are both finite dimensional. Then \(V\) is also finite dimensional and

\[dim \;V =dim \;(\text{ker }T) +dim \;(im \;T) \nonumber \]

In other words, \(dim \;V = nullity \;(T) + rank \;(T)\).

Proof. Every vector in \(im \;T = T(V)\) has the form \(T(\mathbf{v})\) for some \(\mathbf{v}\) in \(V\). Hence let \(\{T(\mathbf{e}_{1}), T(\mathbf{e}_{2}), \dots, T(\mathbf{e}_{r})\}\) be a basis of \(im \;T\), where the \(\mathbf{e}_{i}\) lie in \(V\). Let \(\{\mathbf{f}_{1}, \mathbf{f}_{2}, \dots, \mathbf{f}_{k}\}\) be any basis of \(\text{ker }T\). Then \(dim \;(im \;T) = r\) and \(dim \;(\text{ker }T) = k\), so it suffices to show that \(B = \{\mathbf{e}_{1}, \dots, \mathbf{e}_{r}, \mathbf{f}_{1}, \dots, \mathbf{f}_{k}\}\) is a basis of \(V\).

1. \(B\) spans \(V\). If \(\mathbf{v}\) lies in \(V\), then \(T(\mathbf{v})\) lies in \(im \;V\), so

   \[T(\mathbf{v}) = t_{1}T(\mathbf{e}_1) + t_{2}T(\mathbf{e}_2) + \cdots + t_{r}T(\mathbf{e}_r) \quad t_i \mbox{ in } \mathbb{R} \nonumber \]

2. \(B\) is linearly independent. Suppose that \(t_{i}\) and \(s_{j}\) in \(\mathbb{R}\) satisfy

   \[\label{eq:dimthmproof} t_{1}\mathbf{e}_{1} + \cdots + t_{r}\mathbf{e}_r + s_{1}\mathbf{f}_1 + \cdots + s_{k}\mathbf{f}_k = \mathbf{0} \]

   \[s_{1}\mathbf{f}_1 + \cdots + s_{k}\mathbf{f}_k = \mathbf{0} \nonumber \]

   so \(s_{1} = \cdots = s_{k} = 0\) by the independence of \(\{\mathbf{f}_{1}, \dots, \mathbf{f}_{k}\}\). This proves that \(B\) is linearly independent.

Note that the vector space \(V\) is not assumed to be finite dimensional in Theorem [thm:021499]. In fact, verifying that \(\text{ker }T\) and \(im \;T\) are both finite dimensional is often an important way to prove that \(V\) is finite dimensional.

Note further that \(r + k = n\) in the proof so, after relabelling, we end up with a basis

\[B = \{\mathbf{e}_1, \ \mathbf{e}_2, \ \dots, \ \mathbf{e}_r, \ \mathbf{e}_{r+1}, \ \dots, \ \mathbf{e}_n \} \nonumber \]

of \(V\) with the property that \(\{\mathbf{e}_{r+1}, \dots, \mathbf{e}_{n}\}\) is a basis of \(\text{ker }T\) and \(\{T(\mathbf{e}_{1}), \dots, T(\mathbf{e}_{r})\}\) is a basis of \(im \;T\). In fact, if \(V\) is known in advance to be finite dimensional, then any basis \(\{\mathbf{e}_{r+1}, \dots, \mathbf{e}_{n}\}\) of \(\text{ker }T\) can be extended to a basis \(\{\mathbf{e}_{1}, \mathbf{e}_{2}, \dots, \mathbf{e}_{r}, \mathbf{e}_{r+1}, \dots, \mathbf{e}_{n}\}\) of \(V\) by Theorem [thm:019430]. Moreover, it turns out that, no matter how this is done, the vectors \(\{T(\mathbf{e}_{1}), \dots, T(\mathbf{e}_{r})\}\) will be a basis of \(im \;T\). This result is useful, and we record it for reference. The proof is much like that of Theorem \(\PageIndex{4}\) and is left as Exercise \(\PageIndex{26}\).

Theorem \(\PageIndex{5}\)

Let \(T : V \to W\) be a linear transformation, and let \(\{\mathbf{e}_{1}, \dots, \mathbf{e}_{r}, \mathbf{e}_{r+1}, \dots, \mathbf{e}_{n}\}\) be a basis of \(V\) such that \(\{\mathbf{e}_{r+1}, \dots, \mathbf{e}_{n}\}\) is a basis of \(\text{ker }T\). Then \(\{T(\mathbf{e}_{1}), \dots, T(\mathbf{e}_{r})\}\) is a basis of \(im \;T\), and hence \(r = rank \;T\).

The dimension theorem is one of the most useful results in all of linear algebra. It shows that if either \(dim \;(\text{ker }T)\) or \(dim \;(im \;T)\) can be found, then the other is automatically known. In many cases it is easier to compute one than the other, so the theorem is a real asset. The rest of this section is devoted to illustrations of this fact. The next example uses the dimension theorem to give a different proof of the first part of Theorem [thm:015561].

Example \(\PageIndex{7}\)

Let \(A\) be an \(m \times n\) matrix of \(rank \;r\). Show that the space \(null \;A\) of all solutions of the system \(A\mathbf{x} = \mathbf{0}\) of \(m\) homogeneous equations in \(n\) variables has dimension \(n - r\).

Solution

The space in question is just \(\text{ker }T_{A}\), where \(T_{A} : \mathbb{R}^n \to \mathbb{R}^m\) is defined by \(T_{A}(\mathbf{x}) = A\mathbf{x}\) for all columns \(\mathbf{x}\) in \(\mathbb{R}^n\). But \(dim \;(im \;T_{A}) = rank \;T_{A} = rank \;A = r\) by Example [exa:021363], so \(dim \;(\text{ker }T_{A}) = n - r\) by the dimension theorem.

Example \(\PageIndex{8}\)

If \(T : V \to W\) is a linear transformation where \(V\) is finite dimensional, then

\[dim \;(\text{ker }T) \leq dim \;V \quad \mbox{and} \quad dim \;(im \;T) \leq dim \;V \nonumber \]

Indeed, \(dim \;V =dim \;(\text{ker }T) +dim \;(im \;T)\) by Theorem \(\PageIndex{4}\). Of course, the first inequality also follows because \(\text{ker }T\) is a subspace of \(V\).

Solution

Add example text here.

Example \(\PageIndex{9}\)

Let \(D :\|{P}_{n} \to\|{P}_{n-1}\) be the differentiation map defined by \(D\left[p(x)\right] = p^\prime(x)\). Compute \(\text{ker }D\) and hence conclude that \(D\) is onto.

Solution

Because \(p^\prime(x) = 0\) means \(p(x)\) is constant, we have \(dim \;(\text{ker }D) = 1\). Since \(dim \;\textbf{P}_{n} = n + 1\), the dimension theorem gives

\[dim \;(im \;D) = (n + 1) -dim \;(\text{ker }D) = n =dim \;(\textbf{P}_{n-1}) \nonumber \]

This implies that \(im \;D =\|{P}_{n-1}\), so \(D\) is onto.

Of course it is not difficult to verify directly that each polynomial \(q(x)\) in \(\textbf{P}_{n-1}\) is the derivative of some polynomial in \(\textbf{P}_{n}\) (simply integrate \(q(x)\)!), so the dimension theorem is not needed in this case. However, in some situations it is difficult to see directly that a linear transformation is onto, and the method used in Example \(\PageIndex{9}\) may be by far the easiest way to prove it. Here is another illustration.

Example \(\PageIndex{10}\)

Given \(a\) in \(\mathbb{R}\), the evaluation map \(E_{a} :\|{P}_{n} \to \mathbb{R}\) is given by \(E_{a}\left[p(x)\right] = p(a)\). Show that \(E_{a}\) is linear and onto, and hence conclude that \(\{(x - a), (x - a)^{2}, \dots, (x - a)^{n}\}\) is a basis of \(\text{ker }E_{a}\), the subspace of all polynomials \(p(x)\) for which \(p(a) = 0\).

Solution

\(E_{a}\) is linear by Example [exa:020790]; the verification that it is onto is left to the reader. Hence \(dim \;(im \;E_{a}) =dim \;(\mathbb{R}) = 1\), so \(dim \;(\text{ker }E_{a}) = (n + 1) - 1 = n\) by the dimension theorem. Now each of the \(n\) polynomials \((x - a), (x - a)^{2}, \dots, (x - a)^{n}\) clearly lies in \(\text{ker }E_{a}\), and they are linearly independent (they have distinct degrees). Hence they are a basis because \(dim \;(\text{ker }E_{a}) = n\).

We conclude by applying the dimension theorem to the \(rank \;\) of a matrix.

Example \(\PageIndex{11}\)

If \(A\) is any \(m \times n\) matrix, show that \(rank \;A = rank \;A^{T}A = rank \;AA^{T}\).

Solution

It suffices to show that \(rank \;A = rank \;A^{T}A\) (the rest follows by replacing \(A\) with \(A^{T}\)). Write \(B = A^{T}A\), and consider the associated matrix transformations

\[T_A : \mathbb{R}^n \to \mathbb{R}^m \quad \mbox{and} \quad T_B : \mathbb{R}^n \to \mathbb{R}^n \nonumber \]

The dimension theorem and Example [exa:021363] give

\[\begin{aligned} rank \;A &= rank \;T_A =dim \;(im \;T_A) = n -dim \;(\text{ker }T_A) \\ rank \;B &= rank \;T_B =dim \;(im \;T_B) = n -dim \;(\text{ker }T_B)\end{aligned} \nonumber \]

so it suffices to show that \(\text{ker }T_{A} = \text{ker }T_{B}\). Now \(A\mathbf{x} = \mathbf{0}\) implies that \(B\mathbf{x} = A^{T}A\mathbf{x} = \mathbf{0}\), so \(\text{ker }T_{A}\) is contained in \(\text{ker }T_{B}\). On the other hand, if \(B\mathbf{x} = \mathbf{0}\), then \(A^{T}A\mathbf{x} = \mathbf{0}\), so

\[\| A\mathbf{x} \|^2 = (A\mathbf{x})^T(A\mathbf{x}) = \mathbf{x}^{T}A^{T}A\mathbf{x} = \mathbf{x}^T\mathbf{0} = 0 \nonumber \]

This implies that \(A\mathbf{x} = \mathbf{0}\), so \(\text{ker }T_{B}\) is contained in \(\text{ker }T_{A}\).