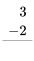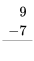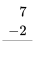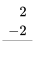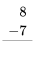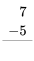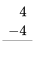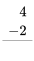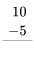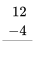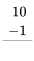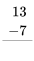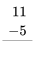3.1: Tema A- Resta

Tema A: Resta

La resta le quita una cantidad a otra cantidad. El resultado de la resta se llama la diferencia.

El signo menos − significa restar.

dice nueve menos tres es seis o nueve quitar tres es seis.

La diferencia entre 9 y 3 es 6.

La resta es lo opuesto a la suma.

Mira los ejemplos:

\begin{array}{cc}
5 + 4 = 9 & 9-4 = 5\\
4+5 = 9 & 9-5 = 4
\end{array}

\begin{array}{cc}
8+3 = 11 & 11-3 = 8\\
3+8 = 11 & 11-8 =3
\end{array}

Los hechos de resta son una herramienta que usarás para hacer preguntas de resta.

Ejercicio 1

Consulta tus datos de resta haciendo los siguientes ejercicios lo más rápido que puedas. Use sus datos de suma para ayudar a encontrar los hechos de resta. Revisa tu trabajo usando la clave de respuesta al final de los ejercicios. Entonces, haz una lista de cualquier dato de resta que desconozcas o que te resulte lento y practícalo.

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

Respuestas al Ejercicio 1

1. 1
2. 1
3. 0
4. 1
5. 6
6. 2
7. 1
8. 5
9. 5
10. 0
11. 1
12. 1

Ejercicio 2

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

Respuestas al Ejercicio 2

1. 4
2. 8
3. 2
4. 2
5. 5
6. 3
7. 2
8. 3
9. 5
10. 1
11. 0
12. 9

Ejercicio 3

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 

Respuestas al Ejercicio 3

1. 4
2. 0
3. 1
4. 1
5. 0
6. 3
7. 1
8. 7
9. 9
10. 1
11. 0
12. 2
13. 0
14. 2
15. 5
16. 1

Ejercicio 4

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 

Respuestas al Ejercicio 4

1. 4
2. 6
3. 5
4. 2
5. 2
6. 3
7. 6
8. 4

Ejercicio 5

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 

Respuestas al Ejercicio 5

1. 9
2. 3
3. 2
4. 5
5. 0
6. 6
7. 8
8. 1

Ejercicio 6

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

Respuestas al Ejercicio 6

1. 4
2. 6
3. 1
4. 5
5. 7
6. 6
7. 2
8. 4
9. 4
10. 2
11. 1
12. 5

Ejercicio 6

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

Respuestas al Ejercicio 6

1. 4
2. 6
3. 1
4. 5
5. 7
6. 6
7. 2
8. 4
9. 4
10. 2
11. 4
12. 5

Ejercicio 7

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 

Respuestas al Ejercicio 7

1. 8
2. 9
3. 5
4. 1
5. 0
6. 8
7. 4
8. 3
9. 9
10. 5
11. 6
12. 2

Practica tus datos de resta usando dominó. Coloca todos los dominós boca abajo.

Ejercicio 8

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 

Respuestas al Ejercicio 8

1. 9
2. 4
3. 6
4. 2
5. 1
6. 7
7. 7
8. 9
9. 1
10. 3
11. 7
12. 5
13. 6
14. 2
15. 6
16. 6

¿Necesitas algo de práctica extra?

• Encuentra un compañero y juega a este juego de cartas.
• Usando una baraja regular de cartas, una jota tendrá once, una reina tendrá doce y un rey trece.
• Baraja las cartas y reparte. Mantén tus cartas en una pila frente a ti.
• Cada jugador voltea una carta.
• Se turnan para restar los números de las tarjetas. Si la persona obtiene la respuesta correcta, esa persona consigue quedarse con las tarjetas. Si la persona recibe la respuesta equivocada el otro jugador recibe las cartas.
• La persona que recoge todas las tarjetas es la ganadora.
• También podrías establecer un límite de tiempo y la persona con más cartas cuando se acabe el tiempo es la ganadora.

Restar a través

Hasta el momento sólo has estado restando números cuando están arriba y abajo o verticales.

Ejemplo:

\ begin {alineado}
9\\
-5\
\ hline 4
\ end {alineado}

Otra forma de restar números es transversal u horizontalmente.

\(9 − 5 = 4\)

Cuando restas números, trabajas de izquierda a derecha.

Ejercicio 9

Practica restar a través u horizontalmente. Consulta tu trabajo usando la clave de respuesta al final del ejercicio.

1. 6 − 3 =
2. 12 − 8 =
3. 4 − 1 =
4. 8 − 6 =
5. 18 − 9 =
6. 11 − 4 =
7. 7 − 2 =
8. 16 − 7 =
9. 10 − 5 =
10. 2 − 0 =
11. 9 − 5 =
12. 17 − 8 =

Respuestas al Ejercicio 9

1. 3
2. 4
3. 3
4. 2
5. 9
6. 7
7. 5
8. 9
9. 5
10. 2
11. 4
12. 9

Ejercicio 10

Practica restar a través u horizontalmente. Consulta tu trabajo usando la clave de respuesta al final del ejercicio.

1. 9 − 6 =
2. 14 − 5 =
3. 8 − 4 =
4. 7 − 1 =
5. 11 − 7 =
6. 5 − 0 =
7. 4 − 3 =
8. 15 − 8 =
9. 11 − 9 =
10. 10 − 2 =
11. 9 − 2 =
12. 8 − 3 =

Respuestas al Ejercicio 10

1. 3
2. 9
3. 4
4. 6
5. 4
6. 5
7. 1
8. 7
9. 2
10. 8
11. 7
12. 5

Ejercicio 11

Practica restar a través u horizontalmente. Consulta tu trabajo usando la clave de respuesta al final del ejercicio.

1. 3 − 2 =
2. 17 − 9 =
3. 14 − 7 =
4. 9 − 3 =
5. 12 − 5 =
6. 8 − 8 =
7. 6 − 1 =
8. 13 − 4 =
9. 11 − 6 =
10. 4 − 0 =
11. 8 − 1 =
12. 16 − 9 =
13. 7 − 0 =
14. 13 − 8 =
15. 12 − 3 =
16. 9 − 4 =
17. 15 − 7 =
18. 10 − 6 =
19. 11 − 5 =
20. 5 − 2 =

Respuestas al Ejercicio 11

1. 1
2. 8
3. 7
4. 6
5. 7
6. 0
7. 5
8. 9
9. 5
10. 4
11. 7
12. 7
13. 7
14. 5
15. 9
16. 5
17. 8
18. 4
19. 6
20. 3

Problemas de palabras

Aprender hechos de resta es muy importante porque una vez que los conoces todos se convierten en una herramienta para usar a la hora de resolver problemas.

Palabras como:

• menos de
• menos
• restado de
• cuantos mas
• cuánto más, y
• diferencia

te dicen que restes los números.

Busque estas palabras al leer problemas de palabras y subrayarlas antes de intentar resolver un problema. Encierra en un círculo la información que se da.

Ejemplo:

Había 14 clavos en una caja. Lu usó 7 de ellos. ¿Cuántos clavos todavía había en la caja?

Había 14 clavos en una caja. Lu usó 7 de ellos. ¿Cuántos clavos todavía había en la caja?

Tienes un círculo de 14 clavos y 7. Esta es la información que utilizará para encontrar la respuesta.

Usted ha subrayado “cuántos”. Estas palabras te dicen que restes.

\ begin {alineada}
14\ texto {uñas}\\
-7\ texto {uñas}\\
\ hline 7\ texto {uñas}
\ end {alineadas}

Ejercicio 12

1. Wolfgang caminó 11 cuadras. Ingrid caminó 6 cuadras. Wolfgang caminó ¿cuánto más lejos que Ingrid?
2. Mika y su padre fueron a pescar. Mika capturó 18 peces y su padre capturó 9 peces. ¿Cuántos peces más capturó Mika?
3. Kuan-Lin estaba haciendo pasteles de luna para la fiesta de clase. Ella necesitaba 15 pasteles para la fiesta. El lunes había hecho 7 pasteles de luna. ¿Cuántos pasteles de luna todavía necesitaba hacer?
4. Malik contó 12 autos en el estacionamiento donde trabajaba. Una hora después, contabilizó sólo 4 autos. ¿Cuántos autos quedan?

Respuestas al Ejercicio 12

1. 5 cuadras
2. 9 peces
3. 8 pasteles de luna
4. 8 autos

Autoexamen del tema A

Marca/21 Objetivo 18/27

1. Encuentra la diferencia. Asegúrate de revisar tus respuestas. (9 marcas)
   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
   7. 
   8. 
   9. 
2. Encuentra la diferencia. Asegúrate de revisar tus respuestas. (6 marcas)
   1. 3 − 2 =
   2. 17 − 9 =
   3. 14 − 7 =
   4. 9 − 3 =
   5. 12 − 5 =
   6. 8 − 8 =
3. Resuelve cada uno de los siguientes problemas de palabras. Asegúrese de incluir la unidad de medida en su respuesta. Asegúrese de rodear la información y subrayar lo que se le pide. (6 marcas, 2 marcas cada una)
   1. Shada capturó 17 peces. Ella le dio 8 peces a su abuela. ¿Cuántos peces le quedan?
   2. Yuan fue a la tienda con 15 dólares para comprar un poco de arroz. El arroz costó $6. ¿Cuánto le quedaba?
   3. Carlo tenía 13 metros de esgrima. Utilizó 8 metros alrededor de su jardín de flores. ¿Cuántos metros le quedan?

Respuestas al tema A Autoexamen

1. 1. 8
   2. 9
   3. 6
   4. 7
   5. 6
   6. 8
   7. 4
   8. 2
   9. 9
2. 1. 1
   2. 8
   3. 7
   4. 6
   5. 7
   6. 0
3. 1. 9 peces
   2. $9
   3. 5 metros