14.5: Ejercicios
- Page ID
- 127682
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades
1. La siguiente tabla muestra las puntuaciones en una prueba de Matemáticas.
a. Completar la tabla de frecuencias para los puntajes del examen de Matemáticas.
b. Construir un histograma de los datos.
c. Construir un gráfico circular de los datos.
| 80 | 50 | 50 | 90 | 70 | 70 | 100 | 60 | 70 | 80 | 70 | 50 |
| 90 | 100 | 80 | 70 | 30 | 80 | 80 | 70 | 100 | 60 | 60 | 50 |
2. A un grupo de adultos se le preguntó cuántos autos tenían en su casa.
a. Complete la tabla de frecuencias para los datos del número de automóvil.
b. Construir un histograma de los datos.
c. Construir un gráfico circular de los datos.
| 1 | 4 | 2 | 2 | 1 | 2 | 3 | 3 | 1 | 4 | 2 | 2 |
| 1 | 2 | 1 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 2 |
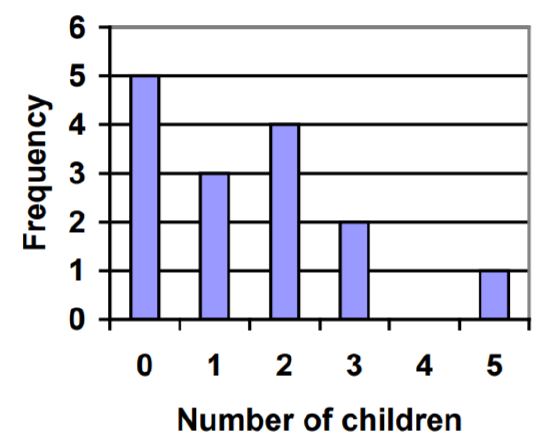
3. A un grupo de adultos se le preguntó cuántos hijos tienen en sus familias. El gráfico de barras a la derecha muestra el número de adultos que indicaron cada número de niños.
a. ¿Cuántos adultos fueron interrogados?
b. ¿Qué porcentaje de los adultos cuestionados tenía 0 hijos?
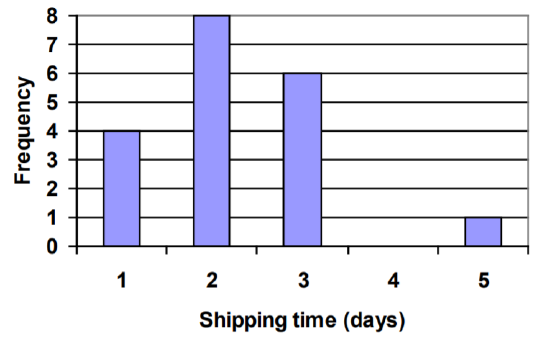
4. Jasmine estaba interesada en cuántos días tardaría un pedido de Netflix en llegar a su puerta. La gráfica a continuación muestra los datos que recopiló.
a. ¿Cuántas películas pidió?
b. ¿Qué porcentaje de las películas llegó en un día?
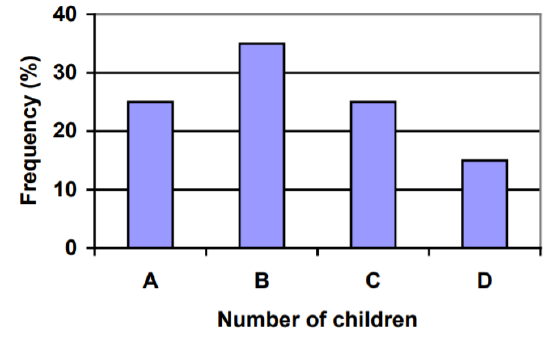
5. El gráfico de barras a continuación muestra el porcentaje de estudiantes que recibieron cada calificación de letras en su último trabajo en inglés. La clase contiene 20 alumnos. ¿Qué número de alumnos obtuvieron una A en su papel?
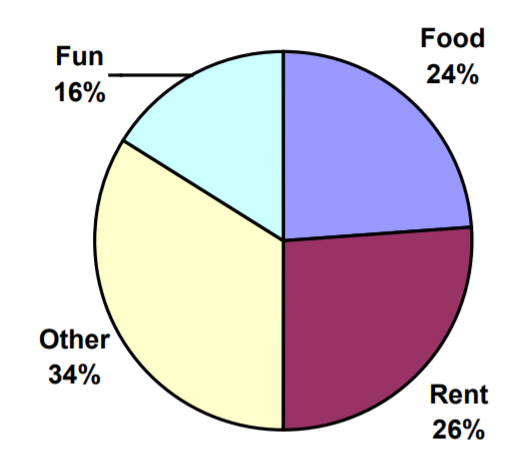
6. Kori clasificó sus gastos para este mes en cuatro categorías: Renta, Comida, Diversión y Otros. Aquí se muestran los porcentajes que gastó en cada categoría. Si gastó un total de 2600 dólares este mes, ¿cuánto gastó en renta?
7. A un grupo de comensales se le preguntó cuánto pagarían por una comida. Sus respuestas fueron: $7.50, $8.25, $9.00, $8.00, $7.25, $7.50, $8.00, $7.00.
a. Encuentra la media
b. Encuentra la mediana
c. Escriba el resumen de 5 números para estos datos
8. Registraste el tiempo en segundos que tardó en que 8 participantes resolvieran un rompecabezas. Los tiempos fueron: 15.2, 18.8, 19.3, 19.7, 20.2, 21.8, 22.1, 29.4.
a. Encuentra la media
b. Encuentra la mediana
c. Escriba el resumen de 5 números para estos datos
9. Refiérase al histograma de la pregunta #3.
a. Calcular el número medio de niños para el grupo encuestado
b. Calcular la mediana del número de niños para el grupo encuestado
c. Escriba el resumen de 5 números para estos datos.
d. Crear parcela de caja.
10. Refiérase al histograma de la pregunta #4.
a. Calcular el número medio de días de envío
b. Calcular la mediana del número de días de envío
c. Escriba el resumen de 5 números para estos datos.
d. Crear parcela de caja.
Conceptos
11. El cuadro de abajo muestra los salarios de Actuarios y CPA. Kendra hace el salario medio de un Actuario. Kelsey obtiene el primer salario cuartil para un CPA. ¿Quién gana más dinero? ¿Cuánto más?
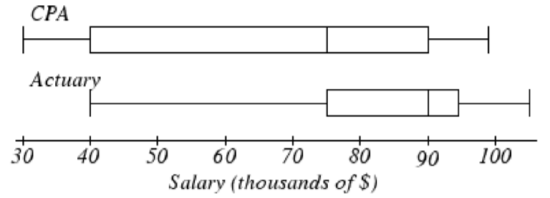
12. Refiriéndose a la gráfica de caja anterior, ¿qué porcentaje de actuarios gana más que el salario medio de un CPA?
Exploración
13. A menudo, las compañías farmacéuticas realizan estudios para determinar la efectividad de un programa de tratamiento. Supongamos que actualmente se encuentra en estudio un nuevo fármaco de anticuerpos contra el SIDA. Se administra a los pacientes una vez que los síntomas del SIDA se han revelado. De interés es el tiempo promedio, en meses, los pacientes viven una vez que comienzan el tratamiento. Dos investigadores siguen cada uno un conjunto diferente de 40 pacientes con SIDA desde el inicio del tratamiento hasta su muerte. Se recogen los siguientes datos (en meses).
Investigador 1:3; 4; 11; 15; 16; 17; 22; 44; 37; 16; 14; 24; 25; 15; 26; 27; 33; 29; 35; 44; 13; 21; 22; 10; 12; 8; 40; 32; 26; 27; 31; 34; 29; 17; 8; 24; 18; 47; 33; 34
Investigador 2:3; 14; 11; 5; 16; 17; 28; 41; 31; 18; 14; 14; 26; 25; 21; 22; 31; 2; 35; 44; 23; 21; 21; 16; 12; 18; 41; 22; 16; 25; 33; 34; 29; 13; 18; 24; 23; 42; 33; 29
a. Crear histogramas comparativos de los datos.
b. Crear diagramas de caja comparativos de los datos.
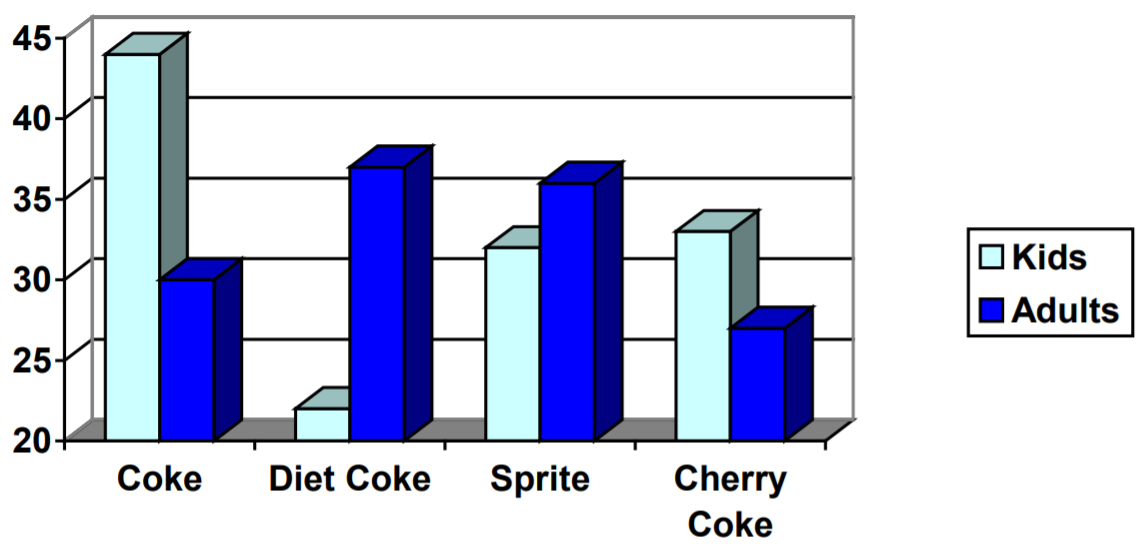
14. A continuación aparece una gráfica que muestra el número de adultos y niños que prefieren cada tipo de refresco. Se encuestaron 130 adultos y niños. Discuta algunas formas en las que se podría mejorar la gráfica a continuación.
15. Conforman tres conjuntos de datos con 5 números cada uno que tengan:
a. la misma media pero diferentes desviaciones estándar.
b. la misma media pero diferentes medianas.
c. la misma mediana pero diferentes medias.
16. Una muestra de 30 puntuaciones de distancia medidas en yardas tiene una media de 7, una varianza de 16 y una desviación estándar de 4.
a. quieres convertir todas tus distancias de yardas a pies, así multiplicas cada puntaje en la muestra por 3. ¿Cuáles son las nuevas medias, mediana, varianza y desviación estándar?
b. Entonces decides que solo quieres mirar la distancia más allá de cierto punto. Así, después de multiplicar las puntuaciones originales por 3, decides restar 4 pies de cada una de las puntuaciones. Ahora, ¿cuáles son las nuevas medias, mediana, varianza y desviación estándar?
17. En tu clase, diseña una encuesta sobre un tema que te interese y dásela a la clase.
a. Resumir los datos, calculando la media y el resumen de cinco números.
b. Crear una representación gráfica de los datos.
c. Escribe varias frases sobre el tema, usando tus estadísticas calculadas como evidencia en tu escritura.


