8.2 Solving Problems With Geometry

Learning Objectives

By the end of this section, you will be able to:

• set up and solve real-world problems that involve geometric shapes
• use the distance formula to find the distance between two points
• use similar triangles to set up equations
• view geometric quantities as functions

In this section, we'll do a survey of problems that require you to know some geometry in order to set up or solve them. As my old professor used to say, "You might want to draw a pitchur." (I went to college in the South.)

To solve a problem involving geometry, try...

1. Sketching a picture of the situation.
2. Labeling any known quantities, dimensions, etc.
3. Identifying what exactly you are trying to find for your answer.
4. Using geometric relationships between the different quantities to solve for your answer.

Here are some examples.

Example \(\PageIndex{1}\)

1. I need to lean a ladder up against my house's exterior wall to reach a second-story window. Because of a bush planted close to the house, I can place the base of the ladder at a distance of 5ft away from the wall. I need the ladder to reach up the wall to a height of 12ft. How long of a ladder do I need?

2. In Minecraft, I am making a rectangular pasture for my rainbow sheep flock. I will use a cliff face as one side of the rectangle, and make the rest of the sides with fencing. If I have 600 blocks of fencing and I divide them evenly amongst the sides, what is the area of my pasture?

3. I am going to make an open box by cutting the corners out of a square piece of cardboard and folding up the sides. If I want the box to have dimensions \(3 \times 3 \times 3\) inches, what size cardboard sheet must I start with?

Solution

1. I sketch my house wall, the ground, and the ladder leaning against the wall. Then, I label the given dimensions on the picture. Since my house stands straight up (hopefully) I know that this is a right triangle.

Now, I identify that what I want to know is the length of the ladder, which is the hypotenuse of my right triangle. You can either use the Pythagorean Theorem to find that length, or notice that this is a special (5, 12, 13) right triangle, so the ladder length must be 13 ft.

2. I sketch the rectangular pasture, with three sides of fencing and one side made by the cliff. If I am splitting 600 blocks equally amongst three sides, each side will get 200 blocks. The picture looks like this:

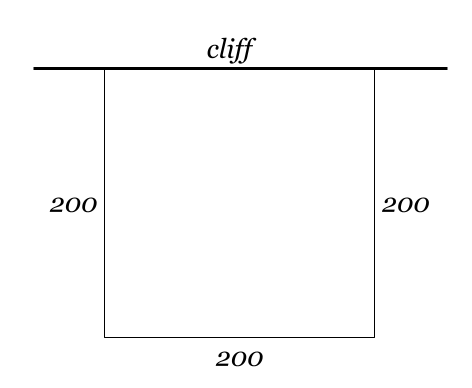
Ope, the area of the interior of the pasture is just the area of a square with side length 200. So the pasture has area \(A = 200^2 = 40000\) blocks.

3. First I draw a square and sketch what it looks like to cut squares out of the corners so I can imagine folding up the sides into a box. I can also sketch the finished box, because I need to connect the dimensions of the finished box to some kind of dimensions on the cardboard diagram...

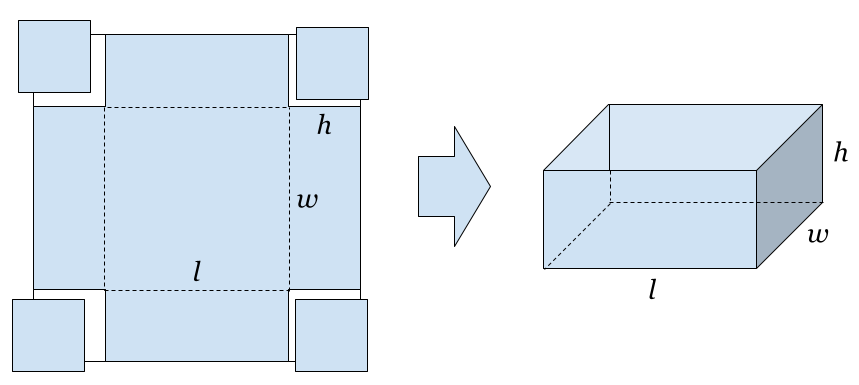
Now that I have a sense, I think about the actual givens in this problem. The original cardboard is square, so its side lengths must be the same, and the squares I'm cutting out of the corners must all be the same size of course, and I want the final box to be \(3 \times 3 \times 3\). I adjust my picture.

Now I identify that I'm supposed to say what the original dimensions of the cardboard square were. Looking at the left side of the picture, I see the big outer square is \(9 \times 9\). Thus that is the size needed to make this box.

Exercise \(\PageIndex{1}\)

1. Two cities are planning to build a lightning rail speed train along the absolute shortest path between them. City A is 300 miles north and 400 miles east of City B. How long will the lightning rail route be?

2. I am building a large rectangular frame for a huge oil painting. I want the outer dimensions of the frame to be 10ft by 12ft, with a rectangular inner opening such that the width of the frame is consistent on all sides, say some value \(x\) ft. I will purchase fancy trim for both the inner and outer edges of the frame. Depending on the width \(x\) chosen, how many feet of trim will I need?

3. My camping tent is a triangular prism: the front and back surfaces are equilateral triangles, with the point of the triangle at the top of course, and the sides are flat rectangles, as is the floor. Over the years, it's gotten a bit saggy, so I want to construct some wooden supports to place straight down the middle of the tent to hold it up, without distorting its shape. If the sides and floor of the tent are all 2 meters wide, what length should I cut my wooden supports to?

Answer

1. The shortest route between two points is the straight line between them. I sketch the locations of the cities and realize that the straight line I'm looking for is the hypotenuse of a right triangle...

Either use the Pythagorean Theorem to find the length of the hypotenuse, or recognize that this is a multiple of the (3, 4, 5) special right triangle. Thus the hypotenuse must be \(500\)mi long.

2. I have a rectangular frame with a rectangular inner opening. The outer dimensions are 10ft by 12ft, and the width of the frame is consistent. I would sketch the situation like this:

If I'm going to add trim on all the inner and outer edges, I need to find the total perimeter of this shape. That is \(P = 2(12)+2(10)+2(10-2x)+2(12-2x) = 88 - 8x\) ft.

3. I imagine a triangular camping tent and sketch a picture of the situation. I want to place supports in the tent, and the question is what height to make them.

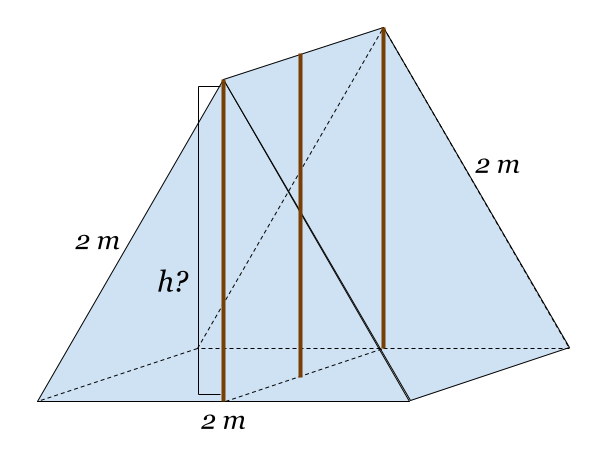
Finding \(h\) is just finding the height of the equilateral triangle with all sides \(2\)m. Using the methods of the last section, we find \(h = \sqrt{3} \approx 1.732\)m.

The Distance Formula

In the exercise above, we had to find the shortest possible distance between two cities, having been given an amount to travel in the vertical direction and an amount to travel in the horizontal direction. We could have imagined these two cities as being on a 2D plane, with City B at \((0,0)\) and City A at \((4,3)\), if we decide that the \(x\)- and \(y\)-values represent hundreds of miles.

We can find the straight line hypotenuse distance between the two points, which is the shortest possible path to travel between them, using the Pythagorean Theorem:

\[ a^2 + b^2 = c^2 \quad \rightarrow \quad (3-0)^2 + (4-0)^2 = c^2 \quad \rightarrow \quad c = \sqrt{ (3-0)^2 + (4-0)^2} = 5 \notag \]

Let's generalize this process to any two points, \( (x_1,y_1)\) and \((x_2,y_2)\).

The Distance Formula

The distance between two points \( A: (x_1,y_1)\) and \(B: (x_2,y_2)\) is given by

\[ d(A,B) = \sqrt{ (x_2-x_1)^2 + (y_2-y_1)^2} \notag \]

Note: It doesn't matter which point you use as the "starting point," aka in what order you subtract the \(x\)-values and \(y\)-values, but you must be consistent in the choice. So you can't do \( (x_2-x_1)^2\) with \((y_1-y_2)^2\), you gotta keep the same order both times.

Example \(\PageIndex{2}\)

My Midwestern hometown is laid out on a grid, as is typical. The streets run north-south and east-west, so you can see my city from a bird's-eye-view as a coordinate plane. I live two blocks east of a coffeeshop, and my friend lives one block west and two blocks north of the same coffeeshop. Find the distance as the crow flies:

1. between my house and the coffeeshop
2. between my friend's house and the coffeeshop
3. between my house and my friend's house

Solution

It's a good idea to sketch a picture. I will place the coffeeshop at the origin \( (0,0)\) because I'm given "the least" information about it in the problem. In general, if locations are given relative to another location, you should put the "reference location" at the origin. My house is two blocks (two steps) to the east (to the right) of the origin. My friend's house is one step west (to the left) of the origin and two steps north (up).

Having identified each location's coordinates, we can just plug into the distance formula. My units are understood to be "one block's length."

1. \( d((2,0),(0,0)) = \sqrt{ (2-0)^2+(0-0)^2} = \sqrt{ 2^2 + 0} = 2 \)
2. \( d((-1,2),(0,0)) = \sqrt{ (-1 -0)^2 + (2-0)^2} = \sqrt{ (-1)^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}\)
3. \( d((2,0),(-1,2)) = \sqrt{ (-1-2)^2 + (2-0)^2} = \sqrt{ (-3)^2 + 2^2} = \sqrt{9 + 4} = \sqrt{13}\)

Exercise \(\PageIndex{2}\)

Given the graphed points, find the distance

1. \(d(A,B)\)
2. \(d(B,A)\)
3. \(d(A,C)\)
4. \( d(B,C)\)
5. \(d( (0,0), B)\)
6. \(d(A,A)\)

Answer

1. \( \sqrt{5}\)
2. \( \sqrt{5}\) (The distance between two points is the same, in any order, bc it's a positive measured quantity.)
3. \( \sqrt{8}\)
4. \( 5\)
5. \( \sqrt{8}\)
6. \( 0\) (The distance from a point to itself is of course always 0.)

Similar Triangles

A geometric concept that comes up a lotttt in setting up Calc I problems, and which unfortunately many students forget about, is the proportionality of similar triangles. Similar triangles are triangles that have exactly all the same interior angles. You will notice that similar triangles look "like the same shape" but scaled up or down.

In math symbols, you represent a triangle with vertices at points A, B, and C as "\(\Delta ABC\)" and if two triangles are similar, we write

\[ \Delta ABC \sim \Delta DEF \notag \]

making sure to "line up" the corresponding parts when we write the names. See the diagram below.

Similar Triangles

The corresponding sides of similar triangles are proportional. So if \(\Delta ABC \sim \Delta DEF \), we have

\[ \frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} \notag \]

Any legal manipulation of these proportions is also true, of course. For example, "\(\dfrac{AB}{DE} = \dfrac{BC}{EF}\)" is saying, "The ratio of the big triangle's side \(AB\) to the small triangle's corresponding side \(DE\) is the same as the ratio of the big triangle's side \(BC\) to the small triangle's corresponding side \(EF\)." But of course, by algebraic manipulation, we have

\[ \frac{AB}{DE} = \frac{BC}{EF} \quad \rightarrow \quad \textcolor{blue}{DE} \cdot \textcolor{red}{\frac{1}{BC}} \cdot \frac{AB}{DE} = \frac{BC}{EF} \cdot \textcolor{red}{\frac{1}{BC}} \cdot \textcolor{blue}{DE} \quad \rightarrow \quad \frac{AB}{BC} = \frac{DE}{EF} \notag \]

The English translation of this proportion is, "The ratio of two sides of the big triangle is the same as the ratio of the corresponding two sides of the small triangle." It all boils down to the same math fact, but different forms might be more natural to use in different scenarios. The example below is like the number one way I use similar triangles in Calc I.

Example \(\PageIndex{3}\)

I have a conical tank holding a certain amount of water, shown below with dimensions. Find \(r\) in terms of \(h\).

Solution

The area of the water's surface will be different depending on the depth of the water in the tank, right? If \(h\) is smaller (lower water level), then \(r\) is smaller, and if \(h\) is bigger (higher water level), then \(r\) will be bigger. We just need to find a way to write down that relationship. The key is to recognize that we can slice out a pair of triangles from this cone:

The large and small triangles are similar because they have all the same angles. How can you tell? They share their smallest angle, and they both have a right angle. Since the interior angles of triangles must sum to \(180^\circ\) total, their third angles must also be equal. Since they are similar triangles, the corresponding sides can be written in proportion(a variety of ways):

\[ \frac{1}{3} = \frac{r}{h} \quad \text{ or } \quad \frac{r}{1} = \frac{h}{3} \quad \text{ etc.} \notag \]

The second option there is a good one to use, because I want to express \(r\) in terms of \(h\), and it's basically there. We write \(r = \frac{h}{3}\) or \(r = \frac{1}{3} h\).

I'll let you practice doing the same type of problem in the exercises section. For now, I want to just connect these problems back to the idea of functions. In the scenario above, we thought of \(h\) as if it were an independent variable. Like the water level can vary, maybe by draining or pumping water into the tank. Then we think of \(h\) as dictating what \(r\) will be. So in a sense, we are thinking of \(r\) as depending on \(h\), an output determined by an input \(h\), or radius "\(r(h)\)" being a function of \(h\).

In the same way, you will often think of quantities like area and volume as functions of some dimension. The area of a circle depends on the size of its radius, so we can think of area, \(A(r) = \pi r^2\), as a function taking input \(r\). In the scenario above, the volume of the cone of water inside the tank can be calculated using the formula \(V = \frac{1}{3}\pi r^2 h \), as we mentioned in the last section. But the example gave us the relationship \(r = \frac{h}{3}\) as well! We can replace \(r\) with what he's equal to, getting

\[ V = \frac{1}{3} \pi \left( \textcolor{red}{\frac{h}{3}} \right)^2 h = \frac{1}{27} \pi h^3 \quad \rightarrow \quad V(h) = \frac{1}{27}\pi h^3 \notag \]

This allows us to think of the volume of the water as a function of \(h\), the height of the water. This concept comes up all the time in optimization problems down the line in calculus, so I wanted to familiarize you with it now.