Properties of Multiplication and Division
Now we’re going to turn our attention to familiar properties of multiplication and division, with the focus still on explaining why these properties are always true.
Here are the four properties you’ll think about:
- Multiplication of whole numbers is commutative.
- Multiplication of whole numbers is associative.
- Multiplication of whole numbers distributes over addition
- The number 1 is an identity for multiplication of whole numbers
For each of the properties, remember to keep straight:
- what the property is called and what it means (the definition),
- some examples that demonstrate the property, and
- an explanation for why the property holds.
Once again, it’s important to distinguish between examples and explanations. They are not the same! Since there are infinitely many whole numbers, it’s impossible to check every case, so examples will never be enough to explain why these properties hold. You have to figure out reasons for these properties to hold, based on what you know about the operations.
1 IS AN IDENTITY FOR MULTIPLICATION
We’ll work out the explanation for the last of these facts, and you will work on the others.
Example: 1 is an Identity for multiplication
Property:
The number 1 is an identity for multiplication of whole numbers.
What it Means (words):
When I multiply a number by 1 (in either order), the product is that number.
What it Means (symbols):
For any whole number m, \[m \times 1 = m \quad \text{and} \quad 1 \times m = m \ldotp \nonumber \]
Examples:
\[1 \times 5 = 5, \qquad 19 \times 1 = 19, \qquad \text{and}\; 1 \times 1 = 1 \ldotp \nonumber \]
Why does the number 1 act this way with multiplication?
Why It’s True, Explanation 1:
Let’s think first about the definition of multiplication as repeated addition:
- m × 1 means to add the number one to itself m times: $$\begin{split} \underbrace{1 + 1 + \cdots + 1}& \\ m\; \text{times} \quad & \end{split}$$So we see that m × 1 = m for any whole number m.
- On the other hand, 1 × m means to add the number m to itself just one time. So 1 × m = m also.
Why It’s True, Explanation 2:
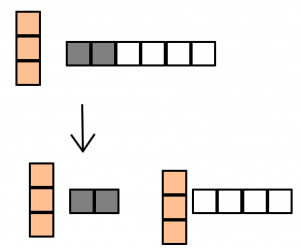
We can also use the number line model to create a justification. If Zed calculates 1×m, he will start at 0 and face the positive direction. He will then take m steps forward, and he will do it just one time. So he lands at m, which means 1 × m = m.
If Zed calculates m × 1, he starts at 0 and faces the positive direction. Then he takes one step forward, and he repeats that mtimes. So he lands at m. We see that m × 1 = m.
Why It’s True, Explanation 3:
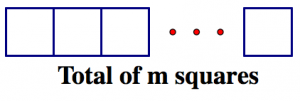
In the area model, m × 1 represents m rows with one square in each row. That makes a total of m squares. So m × 1 = m.
.png?revision=1)
Similarly, 1 × m represents one row of m squares. That’s also a total of m squares. So 1 × m = m.
Think / Pair / Share
The example presented several different explanations. Do you think one is more convincing than the others? Or more clear and easier to understand?
MULTIPLICATION IS COMMUTATIVE
Property: Multiplication whole numbers is commutative.
What it Means (words): When I multiply two whole numbers, switching the order in which I multiply them does not affect the product.
What it Means (symbols): For any two whole numbers a and b, \[a \cdot b = b \cdot a \ldotp \nonumber \]
Problem 18
- Come up with at least three examples to demonstrate the commutativity of multiplication.
- Use our models of multiplication to come up with an explanation. Why does commutativity hold in every case? Note: Your explanation should not use particular numbers. It is not an example!
MULTIPLICATION IS ASSOCIATIVE
Property: Multiplication of whole numbers is associative.
What it Means (words): When I multiply three whole numbers in a given order, the way I group them (to multiply two at a time) doesn’t affect the product.
What it Means (symbols): For any three whole numbers a, b, and c, \[(a \cdot b) \cdot c = a \cdot (b \cdot c) \ldotp \nonumber \]
Problem 19
- Come up with at least three examples to demonstrate the associativity of multiplication.
- Use our models of multiplication to come up with an explanation. Why does associativity hold in every case?
MULTIPLICATION DISTRIBUTES OVER ADDITION
Property: Multiplication distributes over addition.
What it means: The distributive law for multiplication over addition is a little hard to state in words, so we’ll jump straight to the symbols. For any three whole numbers x, y, and z: \[x \cdot (y + z) = x \cdot y + x \cdot z \ldotp \nonumber \]
Examples: We actually did calculations very much like the examples above, when we looked at the area model for multiplication.
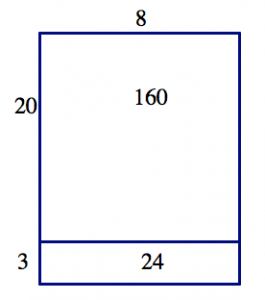
\[8 \cdot (23) = 8 \cdot (20 + 3) = 8 \cdot 20 + 8 \cdot 3 = 160 + 24 = 184 \nonumber \]
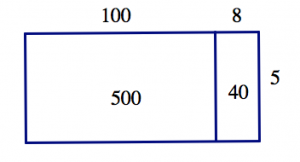
\[5 \cdot (108) = 5 \cdot (100 + 8) = 5 \cdot 100 + 5 \cdot 8 = 500 + 40 = 540 \nonumber \]
Problem 21
Use the distributive law to easily compute each of these in your head (no calculators!). Explain your solutions.
\[45 \times 11 \qquad 63 \times 101 \qquad 172 \times 1001 \nonumber \]
Think / Pair / Share
Use one of our models for multiplication and addition to explain why the distributive rule works every time.
PROPERTIES OF DIVISION
It’s natural to wonder which, if any, of these properties also hold for division (since you know that the operations of multiplication and division are connected).
Example: Is Division Associative?
If division were associative, then for any choice of three whole numbers a, b, and c, we would have
\[a : (b : c) = (a : b) : c \ldotp \nonumber \]
Remember, the parentheses tell you which two numbers to divide first.
Let’s try the example a = 9, b = 3, and c = 1. Then we have:
\[9 : ( 3 : 1 ) = 9 : 3 = 3 \nonumber \]
and
\[(9 : 3 ) : 1 = 3 : 1 = 3 \ldotp \nonumber \]
So is it true? Is division associative? Well, we can’t be sure. This is just one example. But “division is associative” is a universal statement. If it’s true, it has to work for every possible example. Maybe we just stumbled on a good choice of numbers, but it won’t always work.
Let’s keep looking. Try a = 16, b = 4, and c = 2.
\[16 : ( 4 : 2 ) = 16 : 2 = 8 \nonumber \]
and
\[(16 : 4) : 2 = 4 : 2 = 2 \ldotp \nonumber \]
That’s all we need! A single counterexample lets us conclude:
Division is not associative.
What about the other properties? It’s your turn to decide!
Problem 22
- State what it would mean for division to be commutative. You should use words and symbols.
- Decide if division is commutative or not. Carefully explain how you made your decision and how you know you’re right.
Problem 23
- State what it would mean for division to distribute over addition. You definitely want to use symbols!
- Decide if division distributes over addition or not. Carefully explain how you made your decision and how you know you’re right.
Problem 24
- State what it would mean for the number 1 to be an identity for division. You should use words and symbols.
- Decide if 1 is an identity for division or not. Carefully explain how you made your decision and how you know you’re right.
ZERO PROPERTY FOR MULTIPLICATION AND DIVISION
Problem 25
You probably know another property of multiplication that hasn’t been mentioned yet:
If I multiply any number times 0 (in either order), the product is 0. This is sometimes called the zero property of multiplication. Notice that the zero property is very different from the property of being an identity!
1. Write what the zero property means using both words and symbols:
For every whole number n . . .
2. Give at least three examples of the zero property for multiplication.
3. Use one of our models of multiplication to explain why the zero property holds.
Think / Pair / Share
- For each division problem below, turn it into a multiplication problem. Solve those problems if you can. If you can’t, explain what is wrong. $$5 : 0 \qquad 0 : 5 \qquad 7 : 0 \qquad 0 : 7 \qquad 0 : 0$$
- Use your work to explain why we say that division by 0 is undefined.
- Use one of our models of division to explain why division by 0 is undefined.
Four Fact Families
In elementary school, students are often encouraged to memorize “four fact families,” for example:
\[\begin{split} 2 + 3 &= 5 \\ 3 + 2 &= 5 \end{split} \quad \begin{split} 5 - 3 &= 2 \\ 5 - 2 &= 3 \end{split} \nonumber \]
Here’s a different “four fact family”:
\[\begin{split} 2 \cdot 3 &= 6 \\ 3 \cdot 2 &= 6 \end{split} \quad \begin{split} 6 : 3 &= 2 \\ 6 : 2 &= 3 \end{split} \nonumber \]
Think / Pair / Share
- In what sense are these groups of equations “families”?
- Write down at least two more addition / subtraction four fact families.
- Use properties of addition and subtraction to explain why these four fact families are each really one fact.
- Write down at least two more multiplication / division four fact families.
- Use properties of multiplication and division to explain why these four fact families are each really one fact.
Problem 26
- Here’s a true fact in base six: \(2_{six} + 3_{six} = 5_{six}\). Write the rest of this four fact family.
- Here’s a true fact in base six: \(11_{six} - 5_{six} = 2_{six}\). Write the rest of this four fact family.
Going Deeper with Division
So far we’ve been thinking about division in what’s called the quotative model. In the quotative model, we want to make groups of equal size. We know the size of the group, and we ask how many groups. For example, we think of 20 ÷ 4 as:
How many groups of 4 are there in a group of 20?
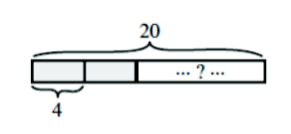
Thinking about four fact families, however, we realize we can turn the question around a bit. We could think about the partitive model of division. In the partitive model, we want to make an equal number of groups. We know how many groups, and we ask the size of the group. In the partitive model, we think of 20 ÷ 4 as:
20 is 4 groups of what size?
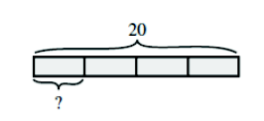
When we know the original amount and the number of parts, we use partitive division to find the size of each part.
When we know the original amount and the size of each part, we use quotative division to find the number of parts.
Here are some examples in word problems:
| Partitive |
Quotative |
|
number of groups known
find the number in each group
|
number in each group known
find the number of groups
|
|
A movie theater made $6450 in one night of ticket sales.
430 people purchased a ticker.
How much does one ticket cost?
|
A movie theater made $6450 in one night of ticket sales.
Each ticket cost $12.50.
How many people purchased a ticket?
|
Think / Pair / Share
For each word problem below:
- Draw a picture to show what the problem is asking.
- Use your picture to help you decide if it is a quotative or a partitive division problem.
- Solve the problem using any method you like.
- David made 36 cookies for the bake sale. He packaged the cookies in boxes of 9. How many boxes did he use?
- David made 36 cookies to share with his friends at lunch. There were 12 people at his lunch table (including David). How many cookies did each person get?
- Liz spent one summer hiking the Appalachin trail. She completed 1,380 miles of the trail and averaged 15 miles per day. How many days was she out hiking that summer?
- On April 1, 2012, Chase Norton became the first person to hike the entire Ko‘olau summit in a single trip. (True story!) It took him eight days to hike all 48 miles from start to finish. If he kept a steady pace, how many miles did he hike each day?
Think / Pair / Share
Write your own word problems: Write one partitive division problem and one quotative division problem. Choose your numbers carefully so that the answer works out nicely. Be sure to solve your problems!
Why think about these two models for division? You won’t be teaching the words partitive and quotative to your students. But recognizing the two kinds of division problems (and being able to come up with examples of each) will make you a better teacher.
It’s important that your students are exposed to both ways of thinking about division, and to problems of both types. Otherwise, they may think about division too narrowly and not really understand what’s going on. If you understand the two kinds of problems, you can more easily diagnose and remedy students’ difficulties.
Most of the division problems we’ve looked at so far have come out evenly, with no remainder. But of course, that doesn’t always happen! Sometimes, a whole number answer makes sense, and the context of the problem should tell you which whole number is the right one to choose.
Problem 27
What is 43 : 4?
- Write a problem that uses the computation 43 : 4 and gives 10 as the correct answer.
- Write a problem that uses the computation 43 : 4 and gives 11 as the correct answer.
- Write a problem that uses the computation 43 : 4 and gives 10.75 as the correct answer.
We can think about division with remainder in terms of some of our models for operations. For example, we can calculate that 23 : 4 = 5 R3. We can picture it this way:
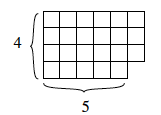
\[23 = 5 \cdot 4 + 3 \ldotp \nonumber \]
Think / Pair / Share
- Explain how the picture above illustrates 23 = 5 · 4 + 3. Where do you see the remainder of 3 in the picture?
- Explain the connection between these two equations. $$23 : 4 = 5\; \text{R} 3 \quad \text{and} \quad 23 = 5 \cdot 4 + 3 \ldotp$$
- How could you use the number line model to show the calculation 23 = 5 · 4 + 3? What does a “remainder” look like in this model?
- Draw area models for each of these division problems. Find the quotient and remainder. $$40 : 12 \qquad 59 : 10 \qquad 91 : 16$$



.png?revision=1)