7.8: Operations on Decimals
- Last updated
- Save as PDF
- Page ID
- 32495
Of course we can add, subtract, multiply, and divide decimal numbers by rewriting them as fractions and using the algorithms we know there. Of course, sometimes it is a lot more work to convert to fractions than it is to just work directly with the decimals (as long as you know what you’re doing). So let’s think about place value and computing with decimals.
Adding and Subtracting Decimals
Remember that when we used the “Dots & Boxes” model to add, it looked like this.
163 + 489
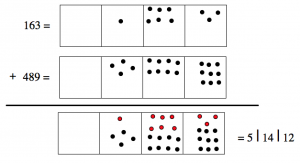
We then perform explosions until there are fewer than ten dots in each box, and we find that: \[163 + 489 = 652 \ldotp \nonumber \]
Subtraction was a little more complicated.
921 – 551
We start with the representation of 921:
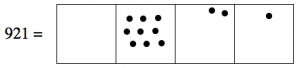
Since we want to “take away” 551, that means we take away five dots from the hundreds box, leaving four dots.
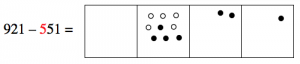
Now we want to take away five dots from the tens box, but we can’t do it! There are only two dots there. What can we do? Well, we still have some hundreds, so we can “unexplode” a hundreds dot, and put ten dots in the tens box instead. Then we’ll be able to take five of them away, leaving seven.
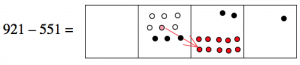
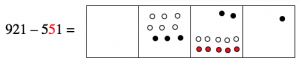
(Notice that we also have one less dot in the hundreds box; there’s only three dots there now.)
Now we want to take one dot from the ones box, and that leaves no dots there.
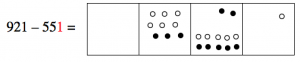
We conclude that: 921 - 551 = 370.
On Your Own
Work on the following exercises on your own or with a partner.
- For each calculation, draw a “Dots & Boxes” model and use it to find the result of the calculation. $$\begin{split} &3.56 + 7.95 \quad 1.452 + 32.27 \quad 3.0205 + 409.2019 \\ &15.225 - 7.209 \quad 14.793 - 8.95 \quad 12.5 - 3.0002 \ldotp \end{split}$$
- For each calculation below, add the decimals quickly using the same reasoning as in the previous problems. $$0.0066 + 0.9 \qquad 0.25 + 0.0088 \qquad 0. \overline{20} + 0. \overline{01} \ldotp$$
Think / Pair / Share
- Chloe added 0.2 and 0.02 and got an answer of 0.4. What was Chloe’s likely mistake? As her teacher, how could you help Chloe understand the operation of addition better?
- In elementary school, students are taught to add and subtract decimals by “lining up the decimal points.” Use the “Dots & Boxes” model to explain why this shorthand makes sense.
Multiplying and Dividing: Powers of 10
Let’s quickly review the “Dots & Boxes” model for multiplication of whole numbers before we get back to talking about decimals.
243192 × 4
If we want to compute 243192 × 4, it helps to remember what multiplication means. One interpretation is: I want to add 243192 to itself a total of four times. So there will be:
- 2 × 4 dots in the ones place,
- 9 × 4 dots in the tens place,
- 1 × 4 dots in the hundreds place,
- and so on.
Here’s the start of the computation:
\[243192 \times 4 = 8\; | \; 16\; | \; 12\; | \; 4\; | \; 36\; | \; 8 \ldotp \nonumber \]
To finish the computation, we need to do some explosions to write the result as a familiar base 10 number:
\[243192 \times 4 = 972768 \ldotp \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner.
- Do each computation, using reasoning like in the multiplication example above. $$(a)\; 2.3 \times 10 \quad (b)\; 3.56 \times 10 \quad (c)\; 1.452 \times 100 \ldotp$$
- Do each computation, using reasoning like in the “Division and Decimals” examples. $$7.1 \div 10 \qquad 98.55 \div 10 \qquad 145.2 \div 100 \ldotp$$
You know that multiplying a base-ten whole number by 10 results in appending a zero to the right end of the number. Your work above should convince you that this does not work for decimals!
Think / Pair / Share
- Write a new rule that works for both whole numbers and decimals:
If I multiply a whole number or a decimal by 10, a simple way to find the result is
___________________________.
- Justify the claim you made above.
- One can go much further with this thinking. What is the effect of dividing a number written in decimal notation by ten? By one-hundred? Justify what you say.
Multiplying Decimals
You probably know an algorithm for multiplying decimal numbers by hand. But if you think carefully about the algorithm, it should make sense based on what the decimal numbers represent and what it means to multiply. Let’s start by using number sense to think about multiplying whole numbers by decimals.
Think / Pair / Share
Consider the expression
\[16 \times \Box \ldotp \nonumber \]
Fill in the box with a whole number or decimal so that the product is:
- Greater than 100.
- Greater than 64 but less than 100.
- At least 17, but less than 32.
- Equal to 16.
- Greater than 8 but less than 16.
- Less than 8, but greater than 0.
Be sure to justify your answers. You should use your number sense rather than computing by hand or with a calculator!
One way to multiply decimal numbers by converting them to fractions and then using what you know about multiplying fractions. There are other ways to think about multiplying that focus on number sense and place value rather than on the mechanics of computation.
321 × 0.4
Suppose a student wanted to compute 321 × 0.4, but he didn’t already know the standard algorithm. What might she do? Here is one idea:
I know that 321 × 0.4 = 1284. Since I want to multiply by 0.4 and not by 4, my answer should be \(\frac{1}{10}\) of this one. So \[321 \times 0.4 = 128.4 \ldotp \nonumber \]
You should notice that the student is using the associative property of multiplication:
\[321 \times 0.4 = 321 \times \frac{4}{10} = 321 \times \left(4 \times \dfrac{1}{10} \right) = (321 \times 4) \times \frac{1}{10} \ldotp \nonumber \]
Problem 15
For each computation below, the result of the computation is shown correctly, but the decimal point is missing. Use number sense and reasoning to correctly place the decimal point, and briefly justify how you know you’re right.
(Don’t use a calculator, don’t work out the multiplication by hand, and don’t use the trick of “counting the number of decimal places.” Use your number sense!)
\[\begin{split} &(a)\; 855 \times 1.7 = 14535 \qquad (b)\; 549 \times 0.33 = 18117 \\ &(c)\; 2.03 \times 1028 = 208684 \qquad (d)\; 999 \times 0.53 = 52947 \\ &(e)\; 30.02 \times 472 = 1416944 \qquad (f)\; 173 \times 0.09 = 1557 \ldotp \end{split} \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner.
- Write each number given as a fraction. (Write them as “improper fractions,” not “mixed numbers.”) $$\begin{split} &(a)\;15.2 \qquad (b)\; 3.43 \\ &(c)\; 0.0021 \qquad (d)\; 13.02026 \ldotp \end{split}$$
- In exercise (1) above, how does the number of digits to the right of the decimal point compare to the number of zeros in the denominator? Use what you know about place value to explain why your answer is always true (not just for the examples above).
- Find each product. $$\begin{split} &(a)\; 10 \times 10000 \qquad (b)\; 100 \times 1000 \\ &(c)\; 100000 \times 1000 \qquad (d)\; 10^{m} \times 10^{n} \ldotp \end{split}$$
- In exercise (3) above, how is the number of zeros in the product related to the number of zeros in the two factors? Use what you know about place value to explain why your answer is always true (not just for the examples above).
- If you write 0.037 as a fraction, how many zeros would be in the denominator?
- What if you write 0.59 as a fraction,how many zeros would be in the denominator?
- How many zeros would be in the denominator of the product of 0.037 and 0.59? (Don’t compute the product to answer this question!)
- Use the fact that 37 × 59 = 2183 and your answers to the exercises above to find 0.037 × 0.59. Explain how you got your answer.
Standard multiplication algorithm
The standard algorithm for multiplying decimal numbers can be described this way:
Step 1
Compute the product as if the two factors were whole numbers. (Ignore the decimal points.)
Step 2
Count the number of digits to the right of the decimal point in each factor, and add those numbers together. Call the result .
Step 3
The sum that you found in Step 2 will be the number of digits to the right of the decimal point in the product. So place the decimal point according by counting the appropriate number of places from the right.
Think / Pair / Share
- Write down two examples of multiplying decimal numbers using the standard algorithm above.
- Use what you know about place value, fractions, and multiplication to carefully explain why the standard algorithm described above makes sense.
Dividing Decimals
As you might expect, dividing decimals is more complicated to explain than any of the other operations. It’s hard to adapt our “Dots & Boxes” model for division. Suppose we want to compute 15.37 ÷ 0.013. We can certainly draw the picture for 15.37, but how could we make groups of 0.013 dots?
Think / Pair / Share
Let’s start by sharing what you already know. Perform this computation (by hand, not with a calculator), showing all of your work. Explain your method to a partner, and see if your partner computed the same way.
\[0.0351 \div 0.074 \ldotp \nonumber \]
On Your Own
Work on the following exercises on your own or with a partner.
- Explain why these two fractions are equivalent. $$\frac{12.33}{44.1} \quad and \quad \frac{123.3}{441} \ldotp$$
- Explain why these two division computations give the same result. $$12.33 \div 44.1 \quad and \quad 123.3 \div 441 \ldotp$$
- Explain why these three fractions are equivalent. $$\frac{325.5}{75.133}, \quad \frac{3255}{751.33}, \quad and \quad \frac{32550}{7513.3} \ldotp$$
- Explain why these three division computations give the same result. $$325.5 \div 75.133, \quad 3255 \div 751.33, \quad and \quad 32550 \div 7513.3 \ldotp$$
- Fill in the box to make the equation true. Be sure to justify your answer. $$\frac{325.5}{75.133} = \frac{\Box}{75133} \ldotp$$
Standard division algorithm
The standard algorithm for dividing numbers represented by finite decimal expansions is something like this:
Step 1
Move the decimal point of the divisor to the end of the number.
Step 2
Move the decimal point of the dividend the same number of positions (the same distance and direction).
Step 3
Divide the new decimal dividend (from Step 2) by the new whole number divisor (from Step 1). Since we’re dividing by a whole number, our standard methods make sense.
This is a pretty mechanical description, and doesn’t give a lot of insight into why this algorithm works.
Think / Pair / Share
Write down at least two examples of computing with the algorithm described above. (Make up your own numbers to test. Be sure to show every step clearly.) You can do the division by drawing a “Dots & Boxes” picture or by another method (but don’t use a calculator). Then answer these more general questions.
- Suppose you want to compute a ÷ b where a and b are decimal numbers. Carefully explain why (10 • a) ÷ (10 • b) will give the same result.
- Suppose you want to compute a ÷ b where a and b are decimal numbers. Carefully explain why (100 • a) ÷ (100 • b) will give the same result.
- Suppose you want to compute a ÷ b where
and
are decimal numbers. Carefully explain why (10k • a) ÷ (10k • b) will give the same result.
- Suppose b has a finite decimal expansion. Carefully explain why you can find a power of 10 so that 10k • b is a whole number.
Problem 16
Carefully explain why the algorithm described above in three steps works for computing division of decimal numbers. You need to explain what is going on when you “move the decimal point” in Steps 1 and 2, and why the result you compute in Step 3 is the same as the original problem.

