9.E: Systems of Equations and Inequalities (Exercises)
- Last updated
- Nov 4, 2018
- Save as PDF
- Page ID
- 13543
( \newcommand{\kernel}{\mathrm{null}\,}\)
9.1: Systems of Linear Equations: Two Variables
Verbal
1) Can a system of linear equations have exactly two solutions? Explain why or why not.
- Answer
-
No, you can either have zero, one, or infinitely many. Examine graphs.
2) If you are performing a break-even analysis for a business and their cost and revenue equations are dependent, explain what this means for the company’s profit margins.
3) If you are solving a break-even analysis and get a negative break-even point, explain what this signifies for the company?
- Answer
-
This means there is no realistic break-even point. By the time the company produces one unit they are already making profit.
4) If you are solving a break-even analysis and there is no break-even point, explain what this means for the company. How should they ensure there is a break-even point?
5) Given a system of equations, explain at least two different methods of solving that system.
- Answer
-
You can solve by substitution (isolating x or y), graphically, or by addition.
Algebraic
For the exercises 6-10, determine whether the given ordered pair is a solution to the system of equations.
6) 5x−y=4x+6y=2 and (4,0)
7) −3x−5y=13−x+4y=10 and (−6,1)
- Answer
-
Yes
8) 3x+7y=12x+4y=0 and (2,3)
9) −2x+5y=72x+9y=7 and (−1,1)
- Answer
-
Yes
10) x+8y=433x−2y=−1 and (3,5)
For the exercises 11-20, solve each system by substitution.
11) x+5y=52x+3y=4
- Answer
-
(−1,2)
12) 3x−2y=185x+10y=−10
13) 4x+2y=−103x+9y=0
- Answer
-
(−3,1)
14) 2x+4y=−3.89x−5y=1.3
15) −2x+3y=1.2−3x−6y=1.8
- Answer
-
(−35,0)
16) x−0.2y=1−10x+2y=5
17) 3x+5y=930x+50y=−90
- Answer
-
No solutions exist
18) −3x+y=212x−4y=−8
19) 12x+13y=1616x+14y=9
- Answer
-
(725,1325)
20) −14x+32y=11−18x+13y=3
For the exercises 21-30, solve each system by addition.
21) −2x+5y=−427x+2y=30
- Answer
-
(6,−6)
22) 6x−5y=−342x+6y=4
23) 5x−y=−2.6−4x−6y=1.4
- Answer
-
(−12,110)
24) 7x−2y=34x+5y=3.25
25) −x+2y=−15x−10y=6
- Answer
-
No solutions exist
26) 7x+6y=2−28x−24y=−8
27) 56x+14y=018x−12y=−43120
- Answer
-
(−15,23)
28) 13x+19y=29−12x+45y=−13
29) −0.2x+0.4y=0.6x−2y=−3
- Answer
-
(x,x+32)
30) −0.1x+0.2y=0.65x−10y=1
For the exercises 31-40, solve each system by any method.
31) 5x+9y=16x+2y=4
- Answer
-
(−4,4)
32) 6x−8y=−0.63x+2y=0.9
33) 5x−2y=2.257x−4y=3
- Answer
-
(12,18)
34) x−512y=−5512−6x+52y=552
35) 7x−4y=762x+4y=13
- Answer
-
(16,0)
36) 3x+6y=112x+4y=9
37) 73x−16y=2−216x+312y=−3
- Answer
-
(x,2(7x−6))
38) 12x+13y=1332x+14y=−18
39) 2.2x+1.3y=−0.14.2x+4.2y=2.1
- Answer
-
(−56,43)
40) 0.1x+0.2y=20.35x−0.3y=0
Graphical
For the exercises 41-45, graph the system of equations and state whether the system is consistent, inconsistent, or dependent and whether the system has one solution, no solution, or infinite solutions.
41) 3x−y=0.6x−2y=1.3
- Answer
-
Consistent with one solution
42) −x+2y=42x−4y=1
43) x+2y=72x+6y=12
- Answer
-
Consistent with one solution
44) 3x−5y=7x−2y=3
45) 3x−2y=5−9x+6y=−15
- Answer
-
Dependent with infinitely many solutions
Technology
For the exercises 46-50, use the intersect function on a graphing device to solve each system. Round all answers to the nearest hundredth.
46) 0.1x+0.2y=0.3−0.3x+0.5y=1
47) −0.01x+0.12y=0.620.15x+0.20y=0.52
- Answer
-
(−3.08,4.91)
48) 0.5x+0.3y=40.25x−0.9y=0.46
49) 0.15x+0.27y=0.39−0.34x+0.56y=1.8
- Answer
-
(−1.52,2.29)
50) −0.71x+0.92y=0.130.83x+0.05y=2.1
Extensions
For the exercises 51-55, solve each system in terms of A,B,C,D, and F where A−F are nonzero numbers. Note that A≠B and AE≠BD.
51) x+y=Ax−y=B
- Answer
-
(A+B2,A−B2)
52) x+Ay=1x+By=1
53) Ax+y=0Bx+y=1
- Answer
-
(−1A−B,AA−B)
54) Ax+By=Cx+y=1
55) Ax+By=CDx+Ey=F
- Answer
-
(CE−BFBD−AE,AF−CDBD−AE)
Real-World Applications
For the exercises 56-60, solve for the desired quantity.
56) A stuffed animal business has a total cost of production C=12x+30 and a revenue function R=20x. Find the break-even point.
57) A fast-food restaurant has a cost of production C(x)=11x+120 and a revenue function R(x)=5x. When does the company start to turn a profit?
- Answer
-
They never turn a profit.
58) A cell phone factory has a cost of productiona C(x)=150x+10,000 and a revenue function R(x)=200x. What is the break-even point?
59) A musician charges C(x)=64x+20,000, where x is the total number of attendees at the concert. The venue charges $80 per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
- Answer
-
(1,250,100,000)
60) A guitar factory has a cost of production C(x)=75x+50,000. If the company needs to break even after 150 units sold, at what price should they sell each guitar? Round up to the nearest dollar, and write the revenue function.
For the exercises 61-77, use a system of linear equations with two variables and two equations to solve.
61) Find two numbers whose sum is 28 and difference is 13.
- Answer
-
The numbers are 7.5 and 20.5
62) A number is 9 more than another number. Twice the sum of the two numbers is 10. Find the two numbers.
63) The startup cost for a restaurant is $120,000, and each meal costs $10 for the restaurant to make. If each meal is then sold for $15, after how many meals does the restaurant break even?
- Answer
-
24,000
64) A moving company charges a flat rate of $150, and an additional $5 for each box. If a taxi service would charge $20 for each box, how many boxes would you need for it to be cheaper to use the moving company, and what would be the total cost?
65) A total of 1,595 first- and second-year college students gathered at a pep rally. The number of freshmen exceeded the number of sophomores by 15. How many freshmen and sophomores were in attendance?
- Answer
-
790 sophomores, 805 freshman
66) 276 students enrolled in a freshman-level chemistry class. By the end of the semester, 5 times the number of students passed as failed. Find the number of students who passed, and the number of students who failed.
67) There were 130 faculty at a conference. If there were 18 more women than men attending, how many of each gender attended the conference?
- Answer
-
56 men, 74 women
68) A jeep and BMW enter a highway running east-west at the same exit heading in opposite directions. The jeep entered the highway 30 minutes before the BMW did, and traveled 7 mph slower than the BMW. After 2 hours from the time the BMW entered the highway, the cars were 306.5 miles apart. Find the speed of each car, assuming they were driven on cruise control.
69) If a scientist mixed 10% saline solution with 60% saline solution to get 25 gallons of 40% saline solution, how many gallons of 10% and 60% solutions were mixed?
- Answer
-
10 gallons of 10% solution, 15 gallons of 60% solution
70) An investor earned triple the profits of what she earned last year. If she made $500,000.48 total for both years, how much did she earn in profits each year?
71) An investor who dabbles in real estate invested 1.1 million dollars into two land investments. On the first investment, Swan Peak, her return was a 110% increase on the money she invested. On the second investment, Riverside Community, she earned 50% over what she invested. If she earned $1 million in profits, how much did she invest in each of the land deals?
- Answer
-
Swan Peak: $750,000, Riverside: $350,000
72) If an investor invests a total of $25,000 into two bonds, one that pays 3% simple interest, and the other that pays 278% interest, and the investor earns $737.50 annual interest, how much was invested in each account?
73) If an investor invests $23,000 into two bonds, one that pays 4% in simple interest, and the other paying 2% simple interest, and the investor earns $710.00 annual interest, how much was invested in each account?
- Answer
-
$12,500 in the first account, $10,500 in the second account.
74) CDs cost $5.96 more than DVDs at All Bets Are Off Electronics. How much would 6 CDs and 2 DVDs cost if 5 CDs and 2 DVDs cost $127.73?
75) A store clerk sold 60 pairs of sneakers. The high-tops sold for $98.99 and the low-tops sold for $129.99. If the receipts for the two types of sales totaled $6,404.40, how many of each type of sneaker were sold?
- Answer
-
High-tops: 45, Low-tops: 15
76) A concert manager counted 350 ticket receipts the day after a concert. The price for a student ticket was $12.50, and the price for an adult ticket was $16.00. The register confirms that $5,075 was taken in. How many student tickets and adult tickets were sold?
77) Admission into an amusement park for 4 children and 2 adults is $116.90. For 6 children and 3 adults, the admission is $175.35. Assuming a different price for children and adults, what is the price of the child’s ticket and the price of the adult ticket?
- Answer
-
Infinitely many solutions. We need more information.
9.2: Systems of Linear Equations: Three Variables
Verbal
1) Can a linear system of three equations have exactly two solutions? Explain why or why not
- Answer
-
No, there can be only one, zero, or infinitely many solutions.
2) If a given ordered triple solves the system of equations, is that solution unique? If so, explain why. If not, give an example where it is not unique.
3) If a given ordered triple does not solve the system of equations, is there no solution? If so, explain why. If not, give an example.
- Answer
-
Not necessarily. There could be zero, one, or infinitely many solutions. For example, (0,0,0) is not a solution to the system below, but that does not mean that it has no solution.
2x+3y−6z=1−4x−6y+12z=−2x+2y+5z=10
4) Using the method of addition, is there only one way to solve the system?
5) Can you explain whether there can be only one method to solve a linear system of equations? If yes, give an example of such a system of equations. If not, explain why not.
- Answer
-
Every system of equations can be solved graphically, by substitution, and by addition. However, systems of three equations become very complex to solve graphically so other methods are usually preferable.
Algebraic
For the exercises 6-10, determine whether the ordered triple given is the solution to the system of equations.
6) 2x−6y+6z=−12x+4y+5z=−1−x+2y+3z=−1 and (0,1,−1)
7) 6x−y+3z=63x+5y+2z=0x+y=0 and (3,−3,−5)
- Answer
-
No
8) 6x−7y+z=2−x−y+3z=42x+y−z=1 and (4,2,−6)
9) x−y=0x−z=5x−y+z=−1 and (4,4,−1)
- Answer
-
Yes
10) −x−y+2z=35x+8y−3z=4−x+3y−5z=−5 and (4,1,−7)
For the exercises 11-16, solve each system by substitution.
11) 3x−4y+2z=−152x+4y+z=162x+3y+5z=20
- Answer
-
(−1,4,2)
12) 5x−2y+3z=202x−4y−3z=−9x+6y−8z=21
13) 5x+2y+4z=9−3x+2y+z=104x−3y+5z=−3
- Answer
-
(−85107,312107,191107)
14) 4x−3y+5z=31−x+2y+4z=20x+5y−2z=−29
15) 5x−2y+3z=4−4x+6y−7z=−13x+2y−z=4
- Answer
-
(1,12,0)
16) 4x+6y+9z=4−5x+2y−6z=37x−4y+3z=−3
For the exercises 17-45, solve each system by Gaussian elimination.
17) 2x−y+3z=17−5x+4y−2z=−462y+5z=−7
- Answer
-
(4,−6,1)
18) 5x−6y+3z=50−x+4y=102x−z=10
19) 2x+3y−6z=1−4x−6y+12z=−2x+2y+5z=10
- Answer
-
(x,127(65−16x),x+2827)
20) 4x+6y−2z=86x+9y−3z=12−2x−3y+z=−4
21) 2x+3y−4z=5−3x+2y+z=11−x+5y+3z=4
- Answer
-
(−4513,1713,−2)
22) 10x+2y−14z=8−x−2y−4z=−1−12x−6y+6z=−12
23) x+y+z=142y+3z=−14−16y−24z=−112
- Answer
-
No solutions exist
24) 5x−3y+4z=−1−4x+2y−3z=0−x+5y+7z=−11
25) x+y+z=02x−y+3z=0x−z=0
- Answer
-
(0,0,0)
26) 3x+2y−5z=65x−4y+3z=−124x+5y−2z=15
27) x+y+z=02x−y+3z=0x−z=1
- Answer
-
(47,−17,−37)
28) 3x−12y−z=−124x+z=3−x+32y=52
29) 6x−5y+6z=3815x−12y+35z=1−4x−32y−z=−74
- Answer
-
(7,20,16)
30) 12x−15y+25z=−131014x−25y−15z=−720−12x−34y−12z=−54
31) −13x−12y−14z=34−12x−14y−12z=2−14x−34y−12z=−12
- Answer
-
(−6,2,1)
32) 12x−14y+34z=014x−110y+25z=−218x+15y−18z=2
33) 45x−78y+12z=1−45x−34y+13z=−8−25x−78y+12z=−5
- Answer
-
(5,12,15)
34) −13x−18y+16z=−43−23x−78y+13z=−233−13x−58y+56z=0
35) −14x−54y+52z=−5−12x−53y+54z=5512−13x−13y+13z=53
- Answer
-
(−5,−5,−5)
36) 140x+160y+180z=1100−12x−13y−14z=−1538x+312y+316z=320
37) 0.1x−0.2y+0.3z=20.5x−0.1y+0.4z=80.7x−0.2y+0.3z=8
- Answer
-
(10,10,10)
38) 0.2x+0.1y−0.3z=0.20.8x+0.4y−1.2z=0.11.6x+0.8y−2.4z=0.2
39) 1.1x+0.7y−3.1z=−1.792.1x+0.5y−1.6z=−0.130.5x+0.4y−0.5z=−0.07
- Answer
-
(12,15,45)
40) 0.5x−0.5y+0.5z=100.2x−0.2y+0.2z=40.1x−0.1y+0.1z=2
41) 0.1x+0.2y+0.3z=0.370.1x−0.2y−0.3z=−0.270.5x−0.1y−0.3z=−0.03
- Answer
-
(12,25,45)
42) 0.5x−0.5y−0.3z=0.130.4x−0.1y−0.3z=0.110.2x−0.8y−0.9z=−0.32
43) 0.5x+0.2y−0.3z=10.4x−0.6y+0.7z=0.80.3x−0.1y−0.9z=0.6
- Answer
-
(2,0,0)
44) 0.3x+0.3y+0.5z=0.60.4x+0.4y+0.4z=1.80.4x+0.2y+0.1z=1.6
45) 0.8x+0.8y+0.8z=2.40.3x−0.5y+0.2z=00.1x+0.2y+0.3z=0.6
- Answer
-
(1,1,1)
Extensions
For the exercises 46-50, solve the system for x,y, and z.
46) x+y+z=3x−12+y−32+z+12=0x−23+y+43+z−33=23
47) 5x−3y−z+12=126x+y−92+2z=−3x+82−4y+z=4
- Answer
-
(128557,23557,428557)
48) x+47−y−16+z+23=1x−24+y+18−z+82=0x+63−y+23+z+42=3
49) x−36+y+22−z−33=2x+24+y−52+z+42=1x+62−y−33+z+1=9
- Answer
-
(6,−1,0)
50) x−13+y+34+z+26=14x+3y−2z=110.02x+0.015y−0.01z=0.065
Real-World Applications
51) Three even numbers sum up to 108. The smaller is half the larger and the middle number is 34 the larger. What are the three numbers?
- Answer
-
24,36,48
52) Three numbers sum up to 147. The smallest number is half the middle number, which is half the largest number. What are the three numbers?
53) At a family reunion, there were only blood relatives, consisting of children, parents, and grandparents, in attendance. There were 400 people total. There were twice as many parents as grandparents, and 50 more children than parents. How many children, parents, and grandparents were in attendance?
- Answer
-
70 grandparents, 140 parents, 190 children
54) An animal shelter has a total of 350 animals comprised of cats, dogs, and rabbits. If the number of rabbits is 5 less than one-half the number of cats, and there are 20 more cats than dogs, how many of each animal are at the shelter?
55) Your roommate, Sarah, offered to buy groceries for you and your other roommate. The total bill was $82. She forgot to save the individual receipts but remembered that your groceries were $0.05 cheaper than half of her groceries, and that your other roommate’s groceries were $2.10 more than your groceries. How much was each of your share of the groceries?
- Answer
-
Your share was $19.95, Sarah’s share was $40, and your other roommate’s share was $22.05.
56) Your roommate, John, offered to buy household supplies for you and your other roommate. You live near the border of three states, each of which has a different sales tax. The total amount of money spent was $100.75. Your supplies were bought with 5% tax, John’s with 8% tax, and your third roommate’s with 9% sales tax. The total amount of money spent without taxes is $93.50. If your supplies before tax were $1 more than half of what your third roommate’s supplies were before tax, how much did each of you spend? Give your answer both with and without taxes.
57) Three coworkers work for the same employer. Their jobs are warehouse manager, office manager, and truck driver. The sum of the annual salaries of the warehouse manager and office manager is $82,000. The office manager makes $4,000 more than the truck driver annually. The annual salaries of the warehouse manager and the truck driver total $78,000. What is the annual salary of each of the co-workers?
- Answer
-
There are infinitely many solutions; we need more information
58) At a carnival, $2,914.25 in receipts were taken at the end of the day. The cost of a child’s ticket was $20.50, an adult ticket was $29.75, and a senior citizen ticket was $15.25. There were twice as many senior citizens as adults in attendance, and 20 more children than senior citizens. How many children, adult, and senior citizen tickets were sold?
59) A local band sells out for their concert. They sell all 1,175 tickets for a total purse of $28,112.50. The tickets were priced at $20 for student tickets, $22.50 for children, and $29 for adult tickets. If the band sold twice as many adult as children tickets, how many of each type was sold?
- Answer
-
500 students, 225 children, and 450 adults
60) In a bag, a child has 325 coins worth $19.50. There were three types of coins: pennies, nickels, and dimes. If the bag contained the same number of nickels as dimes, how many of each type of coin was in the bag?
61) Last year, at Haven’s Pond Car Dealership, for a particular model of BMW, Jeep, and Toyota, one could purchase all three cars for a total of $140,000. This year, due to inflation, the same cars would cost $151,830. The cost of the BMW increased by 8%, the Jeep by 5%, and the Toyota by 12%. If the price of last year’s Jeep was $7,000 less than the price of last year’s BMW, what was the price of each of the three cars last year?
- Answer
-
The BMW was $49,636, the Jeep was $42,636, and the Toyota was $47,727.
62) A recent college graduate took advantage of his business education and invested in three investments immediately after graduating. He invested $80,500 into three accounts, one that paid 4% simple interest, one that paid 318% simple interest, and one that paid 212% simple interest. He earned $2,670 interest at the end of one year. If the amount of the money invested in the second account was four times the amount invested in the third account, how much was invested in each account?
63) You inherit one million dollars. You invest it all in three accounts for one year. The first account pays 3% compounded annually, the second account pays 4% compounded annually, and the third account pays 2% compounded annually. After one year, you earn $34,000 in interest. If you invest four times the money into the account that pays 3% compared to 2%, how much did you invest in each account?
- Answer
-
$400,000 in the account that pays 3% interest, $500,000 in the account that pays 4% interest, and $100,000 in the account that pays 2% interest.
64) You inherit one hundred thousand dollars. You invest it all in three accounts for one year. The first account pays 4% compounded annually, the second account pays 3% compounded annually, and the third account pays 2% compounded annually. After one year, you earn $3,650 in interest. If you invest five times the money in the account that pays 4% compared to 3%, how much did you invest in each account?
65) The top three countries in oil consumption in a certain year are as follows: the United States, Japan, and China. In millions of barrels per day, the three top countries consumed 39.8% of the world’s consumed oil. The United States consumed 0.7% more than four times China’s consumption. The United States consumed 5% more than triple Japan’s consumption. What percent of the world oil consumption did the United States, Japan, and China consume?
- Answer
-
The United States consumed 26.3%, Japan 7.1%, and China 6.4% of the world’s oil.
66) The top three countries in oil production in the same year are Saudi Arabia, the United States, and Russia. In millions of barrels per day, the top three countries produced 31.4% of the world’s produced oil. Saudi Arabia and the United States combined for 22.1% of the world’s production, and Saudi Arabia produced 2% more oil than Russia. What percent of the world oil production did Saudi Arabia, the United States, and Russia produce?
67) The top three sources of oil imports for the United States in the same year were Saudi Arabia, Mexico, and Canada. The three top countries accounted for 47% of oil imports. The United States imported 1.8% more from Saudi Arabia than they did from Mexico, and 1.7% more from Saudi Arabia than they did from Canada. What percent of the United States oil imports were from these three countries?
- Answer
-
Saudi Arabia imported 16.8%, Canada imported 15.1%, and Mexico 15.0%
68) The top three oil producers in the United States in a certain year are the Gulf of Mexico, Texas, and Alaska. The three regions were responsible for 64% of the United States oil production. The Gulf of Mexico and Texas combined for 47% of oil production. Texas produced 3% more than Alaska. What percent of United States oil production came from these regions?
69) At one time, in the United States, 398 species of animals were on the endangered species list. The top groups were mammals, birds, and fish, which comprised 55% of the endangered species. Birds accounted for 0.7% more than fish, and fish accounted for 1.5% more than mammals. What percent of the endangered species came from mammals, birds, and fish?
- Answer
-
Birds were 19.3%, fish were 18.6%, and mammals were 17.1% of endangered species
70) Meat consumption in the United States can be broken into three categories: red meat, poultry, and fish. If fish makes up 4% less than one-quarter of poultry consumption, and red meat consumption is 18.2% higher than poultry consumption, what are the percentages of meat consumption?
9.3: Systems of Nonlinear Equations and Inequalities: Two Variables
Verbal
1) Explain whether a system of two nonlinear equations can have exactly two solutions. What about exactly three? If not, explain why not. If so, give an example of such a system, in graph form, and explain why your choice gives two or three answers.
- Answer
-
A nonlinear system could be representative of two circles that overlap and intersect in two locations, hence two solutions. A nonlinear system could be representative of a parabola and a circle, where the vertex of the parabola meets the circle and the branches also intersect the circle, hence three solutions.
2) When graphing an inequality, explain why we only need to test one point to determine whether an entire region is the solution?
3) When you graph a system of inequalities, will there always be a feasible region? If so, explain why. If not, give an example of a graph of inequalities that does not have a feasible region. Why does it not have a feasible region?
- Answer
-
No. There does not need to be a feasible region. Consider a system that is bounded by two parallel lines. One inequality represents the region above the upper line; the other represents the region below the lower line. In this case, no points in the plane are located in both regions; hence there is no feasible region.
4) If you graph a revenue and cost function, explain how to determine in what regions there is profit.
5) If you perform your break-even analysis and there is more than one solution, explain how you would determine which x-values are profit and which are not.
- Answer
-
Choose any number between each solution and plug into C(x) and R(x). If C(x)<R(x), then there is profit.
Algebraic
For the exercises 6-10, solve the system of nonlinear equations using substitution.
6) x+y=4x2+y2=9
7) y=x−3x2+y2=9
- Answer
-
(0,−3), (3,0)
8) y=xx2+y2=9
9) y=−xx2+y2=9
- Answer
-
(−3√22,3√22), (3√22,−3√22)
10) x=2x2−y2=9
For the exercises 11-15, solve the system of nonlinear equations using elimination.
11) 4x2−9y2=364x2+9y2=36
- Answer
-
(−3,0), (3,0)
12) x2+y2=25x2−y2=1
13) 2x2+4y2=42x2−4y2=25x−10
- Answer
-
(14,−√628), (14,√628)
14) y2−x2=93x2+2y2=8
15) x2+y2+116=2500y=2x2
- Answer
-
(−√3984,1994), (√3984,1994)
For the exercises 16-23, use any method to solve the system of nonlinear equations.
16) −2x2+y=−56x−y=9
17) −x2+y=2−x+y=2
- Answer
-
(0,2), (1,3)
18) x2+y2=1y=20x2−1
19) x2+y2=1y=−x2
- Answer
-
(−√12(√5−1),12(1−√5)), (√12(√5−1),12(1−√5))
20) 2x3−x2=yy=12−x
21) 9x2+25y2=225(x−6)2+y2=1
- Answer
-
(5,0)
22) x4−x2=yx2+y=0
23) 2x3−x2=yx2+y=0
- Answer
-
(0,0)
For the exercises 24-38, use any method to solve the nonlinear system.
24) x2+y2=9y=3−x2
25) x2−y2=9x=3
- Answer
-
(3,0)
26) x2−y2=9y=3
27) x2−y2=9x−y=0
- Answer
-
No Solutions Exist
28) −x2+y=2−4x+y=−1
29) −x2+y=22y=−x
- Answer
-
No Solutions Exist
30) x2+y2=25x2−y2=36
31) x2+y2=1y2=x2
- Answer
-
(−√22,−√22), (−√22,√22), (√22,−√22), (√22,√22)
32) 16x2−9y2+144=0y2+x2=16
33) 3x2−y2=12(x−1)2+y2=1
- Answer
-
(2,0)
34) 3x2−y2=12(x−1)2+y2=4
35) 3x2−y2=12x2+y2=16
- Answer
-
(−√7,−3), (−√7,3), (√7,−3), (√7,3)
36) x2−y2−6x−4y−11=0−x2+y2=5
37) x2+y2−6y=7x2+y=1
- Answer
-
(−√12(√73−5),12(7−√73)), (√12(√73−5),12(7−√73))
38) x2+y2=6xy=1
Graphical
For the exercises 39-40, graph the inequality.
39) x2+y<9
- Answer
-
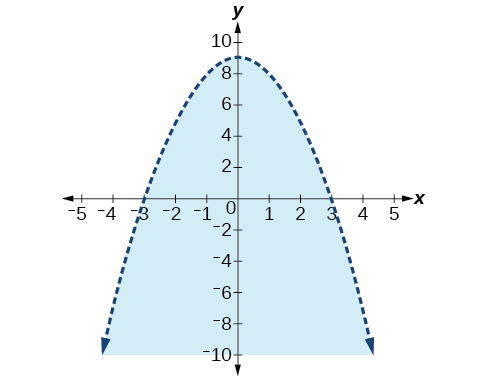
40) x2+y2<4
For the exercises 41-45, graph the system of inequalities. Label all points of intersection.
41) x2+y<1y>2x
- Answer
-
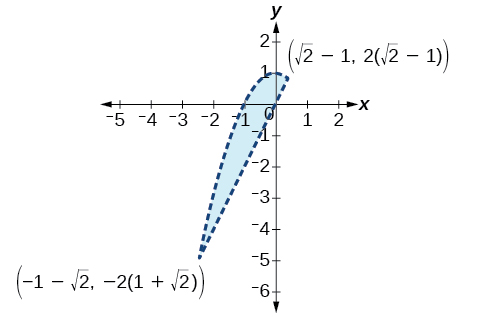
42) x2+y<−5y>5x+10
43) x2+y2<253x2−y2>12
- Answer
-
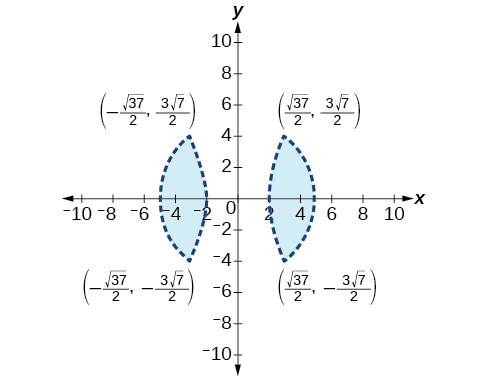
44) x2−y2>−4x2+y2<12
45) x2+3y2>163x2−y2<1
- Answer
-
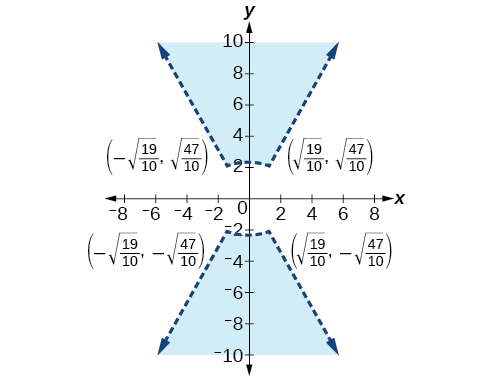
Extensions
For the exercises 46-47, graph the inequality.
46) y≥exy≤ln(x)+5
47) y≤−log(x)y≤ex
- Answer
-
For the exercises 48-52, find the solutions to the nonlinear equations with two variables.
48) 4x2+1y2=245x2−2y2+4=0
49) 6x2−1y2=81x2−6y2=18
- Answer
-
(−2√70383,−2√3529), (−2√70383,2√3529), (2√70383,−2√3529), (2√70383,2√3529)
50) x2−xy+y2−2=0x+3y=4
51) x2−xy−2y2−6=0x2+y2=1
- Answer
-
No Solution Exists
52) x2+4xy−2y2−6=0x=y+2
Technology
For the exercises 53-54, solve the system of inequalities. Use a calculator to graph the system to confirm the answer.
53) xy<1y>√x
- Answer
-
x=0, y>0 and 0<x<1, √x<y<1x
54) x2+y<3y>2x
Real-World Applications
For the exercises 55-, construct a system of nonlinear equations to describe the given behavior, then solve for the requested solutions.
55) Two numbers add up to 300. One number is twice the square of the other number. What are the numbers?
- Answer
-
12,288
56) The squares of two numbers add to 360. The second number is half the value of the first number squared. What are the numbers?
57) A laptop company has discovered their cost and revenue functions for each day: C(x)=3x2−10x+200 and R(x)=−2x2+100x+50. If they want to make a profit, what is the range of laptops per day that they should produce? Round to the nearest number which would generate profit.
- Answer
-
2 - 20 computers
58) A cell phone company has the following cost and revenue functions: C(x)=8x2−600x+21,500 and R(x)=−3x2+480x. What is the range of cell phones they should produce each day so there is profit? Round to the nearest number that generates profit.
9.4: Partial Fractions
Verbal
1) Can any quotient of polynomials be decomposed into at least two partial fractions? If so, explain why, and if not, give an example of such a fraction.
- Answer
-
No, a quotient of polynomials can only be decomposed if the denominator can be factored. For example, 1x2+1 cannot be decomposed because the denominator cannot be factored.
2) Can you explain why a partial fraction decomposition is unique? (Hint: Think about it as a system of equations.)
3) Can you explain how to verify a partial fraction decomposition graphically?
- Answer
-
Graph both sides and ensure they are equal.
4) You are unsure if you correctly decomposed the partial fraction correctly. Explain how you could double-check your answer.
5) Once you have a system of equations generated by the partial fraction decomposition, can you explain another method to solve it? For example if you had 7x+133x2+8x+15=Ax+1+B3x+5 we eventually simplify to 7x+13=A(3x+5)+B(x+1). Explain how you could intelligently choose an x-value that will eliminate either A or B and solve for A and B.
- Answer
-
If we choose x=−1
, ,
Algebraic
For the exercises 6-19, find the decomposition of the partial fraction for the nonrepeating linear factors.
6) 5x+16x2+10x+24
7) 3x−79x2−5x−24
- Answer
-
8x+3−5x−8
8) −x−24x2−2x−24
9) 10x+47x2+7x+10
- Answer
-
1x+5+9x+2
10) x6x2+25x+25
11) 32x−1120x2−13x+2
- Answer
-
35x−2+44x−1
12) x+1x2+7x+10
13) 5xx2−9
- Answer
-
52(x+3)+52(x−3)
14) 10xx2−25
15) 6xx2−4
- Answer
-
\dfrac{3}{x+2}+\dfrac{3}{x-2}
16) \dfrac{2x-3}{x^2-6x+5}
17) \dfrac{4x-1}{x^2-x-6}
- Answer
-
\dfrac{9}{5(x+2)}+\dfrac{11}{5(x-3)}
18) \dfrac{4x+3}{x^2+8x+15}
19) \dfrac{3x-1}{x^2-5x+6}
- Answer
-
\dfrac{8}{x-3}-\dfrac{5}{x-2}
For the exercises 20-30, find the decomposition of the partial fraction for the repeating linear factors.
20) \dfrac{-5x-19}{(x+4)^2}
21) \dfrac{x}{(x-2)^2}
- Answer
-
\dfrac{1}{x-2}-\dfrac{2}{(x-2)^2}
22) \dfrac{7x+14}{(x+3)^2}
23) \dfrac{-24x-27}{(4x+5)^2}
- Answer
-
-\dfrac{6}{4x+5}+\dfrac{3}{(4x+5)^2}
24) \dfrac{-24x-27}{(6x-7)^2}
25) \dfrac{5-x}{(x-7)^2}
- Answer
-
-\dfrac{1}{x-7}-\dfrac{2}{(x-7)^2}
26) \dfrac{5x+14}{2x^2+12x+18}
27) \dfrac{5x^2+20x+8}{2x(x+1)^2}
- Answer
-
\dfrac{4}{x}-\dfrac{3}{2(x+1)}+\dfrac{7}{2(x+1)^2}
28) \dfrac{4x^2+55x+25}{5x(3x+5)^2}
29) \dfrac{54x^3+127x^2+80x+16}{2x^2(3x+2)^2}
- Answer
-
\dfrac{4}{x}+\dfrac{2}{x^2}-\dfrac{3}{3x+2}+\dfrac{7}{2(3x+2)^2}
30) \dfrac{x^3-5x^2+12x+144}{x^2(x^2+12x+36)}
For the exercises 31-43, find the decomposition of the partial fraction for the irreducible nonrepeating quadratic factor.
31) \dfrac{4x^2+6x+11}{(x+2)(x^2+x+3)}
- Answer
-
\dfrac{x+1}{x^2+x+3}+\dfrac{3}{(x+2)}
32) \dfrac{4x^2+9x+23}{(x-1)(x^2+6x+11)}
33) \dfrac{-2x^2+10x+4}{(x-1)(x^2+3x+8)}
- Answer
-
\dfrac{4-3x}{x^2+3x+8}+\dfrac{1}{(x-1)}
34) \dfrac{x^2+3x+1}{(x+1)(x^2+5x-2)}
35) \dfrac{4x^2+17x-1}{(x+3)(x^2+6x+1)}
- Answer
-
\dfrac{2x-1}{x^2+6x+1}+\dfrac{2}{(x+3)}
36) \dfrac{4x^2}{(x+5)(x^2+7x-5)}
37) \dfrac{4x^2+x+3}{x^3 - 1}
- Answer
-
\dfrac{1}{x^2+x+1}+\dfrac{4}{(x-1)}
38) \dfrac{-5x^2+18x-4}{x^3 + 8}
39) \dfrac{3x^2-7x+33}{x^3 + 27}
- Answer
-
\dfrac{2}{x^2-3x+9}+\dfrac{3}{(x+3)}
40) \dfrac{x^2+2x+40}{x^3 - 125}
41) \dfrac{4x^2+4x+12}{8x^3 - 27}
- Answer
-
-\dfrac{1}{4x^2+6x+9}+\dfrac{1}{(2x-3)}
42) \dfrac{-50x^2+5x-3}{125x^3 - 1}
43) \dfrac{-2x^3-30x^2+36x+216}{x^4 + 216x}
- Answer
-
\dfrac{1}{x}+\dfrac{1}{x+6}-\dfrac{4x}{x^2-6x+36}
For the exercises 44-54, find the decomposition of the partial fraction for the irreducible repeating quadratic factor.
44) \dfrac{3x^3+2x^2+14x+15}{(x^2 + 4)^2}
45) \dfrac{x^3+6x^2+5x+9}{(x^2 + 1)^2}
- Answer
-
\dfrac{x+6}{x^2+1}+\dfrac{4x+3}{(x^2+1)^2}
46) \dfrac{x^3-x^2+x-1}{(x^2 - 3)^2}
47) \dfrac{x^2+5x+5}{(x+2)^2}
- Answer
-
\dfrac{x+1}{x+2}+\dfrac{2x+3}{(x+2)^2}
48) \dfrac{x^3+2x^2+4x}{(x^2+2x+9)^2}
49) \dfrac{x^2+25}{(x^2+3x+25)^2}
- Answer
-
\dfrac{1}{x^2+3x+25}-\dfrac{3x}{(x^2+3x+25)^2}
50) \dfrac{2x^3+11x+7x+70}{(2x^2+x+14)^2}
51) \dfrac{5x+2}{x(x^2+4)^2}
- Answer
-
\dfrac{1}{8x}-\dfrac{x}{8(x^2+4)}+\dfrac{10-x}{8(x^2+4)^2}
52) \dfrac{x^4+x^3+8x^2+6x+36}{x(x^2+6)^2}
53) \dfrac{2x-9}{(x^2-x)^2}
- Answer
-
-\dfrac{16}{x}-\dfrac{9}{x^2}+\dfrac{16}{x-1}-\dfrac{7}{(x-1)^2}
54) \dfrac{5x^3-2x+1}{(x^2+2x)^2}
Extensions
For the exercises 55-56, find the partial fraction expansion.
55) \dfrac{x^2+4}{(x+1)^3}
- Answer
-
\dfrac{1}{x+1}-\dfrac{2}{(x+1)^2}+\dfrac{5}{(x+1)^3}
56) \dfrac{x^3-4x^2+5x+4}{(x-2)^3}
For the exercises 57-59, perform the operation and then find the partial fraction decomposition.
57) \dfrac{7}{x+8}+\dfrac{5}{x-2}-\dfrac{x-1}{x^2-6x-16}
- Answer
-
\dfrac{5}{x-2}-\dfrac{3}{10(x+2)}+\dfrac{7}{x+8}-\dfrac{7}{10(x-8)}
58) \dfrac{1}{x-4}-\dfrac{3}{x+6}-\dfrac{2x+7}{x^2+2x-24}
59) \dfrac{2x}{x^2-16}-\dfrac{1-2x}{x^2+6x+8}-\dfrac{x-5}{x^2-4x}
- Answer
-
-\dfrac{5}{4x}-\dfrac{5}{2(x+2)}+\dfrac{11}{2(x+4)}+\dfrac{5}{4(x+4)}
9.5: Matrices and Matrix Operations
Verbal
1) Can we add any two matrices together? If so, explain why; if not, explain why not and give an example of two matrices that cannot be added together.
- Answer
-
No, they must have the same dimensions. An example would include two matrices of different dimensions. One cannot add the following two matrices because the first is a 2\times 2 matrix and the second is a 2\times 3. \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 6 & 5 & 4\\ 3 & 2 & 1 \end{bmatrix} has no sum.
2) Can we multiply any column matrix by any row matrix? Explain why or why not.
3) Can both the products AB and BA be defined? If so, explain how; if not, explain why.
- Answer
-
Yes, if the dimensions of A are m\times n and the dimensions of B are n\times m both products will be defined.
4) Can any two matrices of the same size be multiplied? If so, explain why, and if not, explain why not and give an example of two matrices of the same size that cannot be multiplied together.
5) Does matrix multiplication commute? That is, does AB=BA? If so, prove why it does. If not, explain why it does not.
- Answer
-
Not necessarily. To find AB, we multiply the first row of A by the first column of B to get the first entry of AB. To find BA, we multiply the first row of B by the first column of A to get the first entry of BA. Thus, if those are unequal, then the matrix multiplication does not commute.
Algebraic
For the exercises 6-11, use the matrices below and perform the matrix addition or subtraction. Indicate if the operation is undefined.
A=\begin{bmatrix} 1 & 3\\ 0 & 7 \end{bmatrix}, B=\begin{bmatrix} 2 & 14\\ 22 & 6 \end{bmatrix}, C=\begin{bmatrix} 1 & 5\\ 8 & 92\\ 12 & 6 \end{bmatrix}, D=\begin{bmatrix} 10 & 14\\ 7 & 2\\ 5 & 61 \end{bmatrix}, E=\begin{bmatrix} 6 & 12\\ 14 & 5 \end{bmatrix}, F=\begin{bmatrix} 0 & 9\\ 78 & 17\\ 15 & 4 \end{bmatrix} \nonumber
6) A+B
7) C+D
- Answer
-
\begin{bmatrix} 11 & 19\\ 15 & 94\\ 17 & 67 \end{bmatrix}
8) A+C
9) B-E
- Answer
-
\begin{bmatrix} -4 & 2\\ 8 & 1 \end{bmatrix}
10) C+F
11) D-B
- Answer
-
Undefined; dimensions do not match
For the exercises 12-17, use the matrices below to perform scalar multiplication.
A=\begin{bmatrix} 4 & 6\\ 13 & 12 \end{bmatrix}, B=\begin{bmatrix} 3 & 9\\ 21 & 12\\ 0 & 64 \end{bmatrix}, C=\begin{bmatrix} 16 & 3 & 7 & 18\\ 90 & 5 & 3 & 29 \end{bmatrix}, D=\begin{bmatrix} 18 & 12 & 13\\ 8 & 14 & 6\\ 7 & 4 & 21 \end{bmatrix} \nonumber
12) 5A
13) 3B
- Answer
-
\begin{bmatrix} 9 & 27\\ 63 & 36\\ 0 & 192 \end{bmatrix}
14) -2B
15) -4C
- Answer
-
\begin{bmatrix} -64 & -12 & -28 & -72\\ -360 & -20 & -12 & -116 \end{bmatrix}
16) \dfrac{1}{2}C
17) 100D
- Answer
-
\begin{bmatrix} 1,800 & 1,200 & 1,300\\ 800 & 1,400 & 600\\ 700 & 400 & 2,100 \end{bmatrix}
For the exercises 18-23, use the matrices below to perform matrix multiplication.
A=\begin{bmatrix} -1 & 5\\ 3 & 2 \end{bmatrix}, B=\begin{bmatrix} 3 & 6 & 4\\ -8 & 0 & 12 \end{bmatrix}, C=\begin{bmatrix} 4 & 10\\ -2 & 6\\ 5 & 9 \end{bmatrix}, D=\begin{bmatrix} 2 & -3 & 12\\ 9 & 3 & 1\\ 0 & 8 & -10 \end{bmatrix} \nonumber
18) AB
19) BC
- Answer
-
\begin{bmatrix} 20 & 102\\ 28 & 28 \end{bmatrix}
20) CA
21) BD
- Answer
-
\begin{bmatrix} 60 & 41 & 2\\ -16 & 120 & -216 \end{bmatrix}
22) DC
23) CB
- Answer
-
\begin{bmatrix} -68 & 24 & 136\\ -54 & -12 & 64\\ -57 & 30 & 128 \end{bmatrix}
For the exercises 24-29, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed.
A=\begin{bmatrix} 2 & -5\\ 6 & 7 \end{bmatrix}, B=\begin{bmatrix} -9 & 6\\ -4 & 2 \end{bmatrix}, C=\begin{bmatrix} 0 & 9\\ 7 & 1 \end{bmatrix}, D=\begin{bmatrix} -8 & 7 & -5\\ 4 & 3 & 2\\ 0 & 9 & 2 \end{bmatrix}, E=\begin{bmatrix} 4 & 5 & 3\\ 7 & -6 & -5\\ 1 & 0 & 9 \end{bmatrix} \nonumber
24) A+B-C
25) 4A+5D
- Answer
-
Undefined; dimensions do not match.
26) 2C+B
27) 3D+4E
- Answer
-
\begin{bmatrix} -8 & 41 & -3\\ 40 & -15 & -14\\ 4 & 27 & 42 \end{bmatrix}
28) C-0.5D
29) 100D-10E
- Answer
-
\begin{bmatrix} -840 & 650 & -530\\ 330 & 360 & 250\\ -10 & 900 & 110 \end{bmatrix}
For the exercises 30-40, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. (Hint: A^2=A\cdot A)
A=\begin{bmatrix} -10 & 20\\ 5 & 25 \end{bmatrix}, B=\begin{bmatrix} 40 & 10\\ -20 & 30 \end{bmatrix}, C=\begin{bmatrix} -1 & 0\\ 0 & -1\\ 1 & 0 \end{bmatrix} \nonumber
30) AB
31) BA
- Answer
-
\begin{bmatrix} -350 & 1,050\\ 350 & 350 \end{bmatrix}
32) CA
33) BC
- Answer
-
Undefined; inner dimensions do not match.
34) A^2
35) B^2
- Answer
-
\begin{bmatrix} 1,400 & 700\\ -1,400 & 700 \end{bmatrix}
36) C^2
37) B^2A^2
- Answer
-
\begin{bmatrix} 332,500 & 927,500\\ -227,500 & 87,500 \end{bmatrix}
38) A^2B^2
39) (AB)^2
- Answer
-
\begin{bmatrix} 490,000 & 0\\ 0 & 490,000 \end{bmatrix}
40)(BA)^2
For the exercises 41-49, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. (Hint: A^2=A\cdot A)
A=\begin{bmatrix} 1 & 0\\ 2 & 3 \end{bmatrix}, B=\begin{bmatrix} -2 & 3 & 4\\ -1 & 1 & -5 \end{bmatrix}, C=\begin{bmatrix} 0.5 & 0.1\\ 1 & 0.2\\ -0.5 & 0.3 \end{bmatrix}, D=\begin{bmatrix} 1 & 0 & -1\\ -6 & 7 & 5\\ 4 & 2 & 1 \end{bmatrix} \nonumber
41) AB
- Answer
-
\begin{bmatrix} -2 & 3 & 4\\ -7 & 9 & -7 \end{bmatrix} \nonumber
42) BA
43) BD
- Answer
-
\begin{bmatrix} -4 & 29 & 21\\ -27 & -3 & 1 \end{bmatrix} \nonumber
44) DC
45) D^2
- Answer
-
\begin{bmatrix} -3 & -2 & -2\\ -28 & 59 & 46\\ -4 & 16 & 7 \end{bmatrix} \nonumber
46) A^2
47) D^3
- Answer
-
\begin{bmatrix} 1 & -18 & -9\\ -198 & 505 & 369\\ -72 & 126 & 91 \end{bmatrix} \nonumber
48) (AB)C
49) A(BC)
- Answer
-
\begin{bmatrix} 0 & 1.6\\ 9 & -1 \end{bmatrix} \nonumber
Technology
For the exercises 50-54, use the matrices below to perform the indicated operation if possible. If not possible, explain why the operation cannot be performed. Use a calculator to verify your solution.
A=\begin{bmatrix} -2 & 0 & 9\\ 1 & 8 & -3\\ 0.5 & 4 & 5 \end{bmatrix}, B=\begin{bmatrix} 0.5 & 3 & 0\\ -4 & 1 & 6\\ 8 & 7 & 2 \end{bmatrix}, C=\begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 1 \end{bmatrix} \nonumber
50) AB
51) BA
- Answer
-
\begin{bmatrix} 2 & 24 & -4.5\\ 12 & 32 & -9\\ -8 & 64 & 61 \end{bmatrix} \nonumber
52) CA
53) BC
- Answer
-
\begin{bmatrix} 0.5 & 3 & 0.5\\ 2 & 1 & 2\\ 10 & 7 & 10 \end{bmatrix} \nonumber
54) ABC
Extensions
For the exercises 55-, use the matrix below to perform the indicated operation on the given matrix.
B=\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix} \nonumber
55) B^2
- Answer
-
\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber
56) B^3
57) B^4
- Answer
-
\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber
58) B^5
59) Using the above questions, find a formula for B^n. Test the formula for B^{201} and B^{202}, using a calculator.
- Answer
-
B^n=\begin{cases} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}, & n\text{ even }\\ \\ \begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix}, & n\text{ odd } \end{cases}
9.6: Solving Systems with Gaussian Elimination
Verbal
1) Can any system of linear equations be written as an augmented matrix? Explain why or why not. Explain how to write that augmented matrix.
- Answer
-
Yes. For each row, the coefficients of the variables are written across the corresponding row, and a vertical bar is placed; then the constants are placed to the right of the vertical bar.
2) Can any matrix be written as a system of linear equations? Explain why or why not. Explain how to write that system of equations.
3) Is there only one correct method of using row operations on a matrix? Try to explain two different row operations possible to solve the augmented matrix \left [ \begin{array}{cc|c} 9 & 3 & 0\\ 1 & -2 & 6\\ \end{array} \right ].
- Answer
-
No, there are numerous correct methods of using row operations on a matrix. Two possible ways are the following:
- Interchange rows 1 and 2. Then R_2=R_2-9R_1.
- R_2=R_1-9R_2. Then divide row 1 by 9.
4) Can a matrix whose entry is 0 on the diagonal be solved? Explain why or why not. What would you do to remedy the situation?
5) Can a matrix that has 0 entries for an entire row have one solution? Explain why or why not.
- Answer
-
No. A matrix with 0 entries for an entire row would have either zero or infinitely many solutions.
Algebraic
For the exercises 6-10, write the augmented matrix for the linear system.
6) \begin{align*} 8x-37y &= 8\\ 2x+12y &= 3 \end{align*}
7) \begin{align*} 16y &= 4\\ 9x-y &= 2 \end{align*}
- Answer
-
\left [ \begin{array}{cc|c} 0 & 16 & 4\\ 9 & -1 & 2\\ \end{array} \right ]
8) \begin{align*} 3x+2y+10z &= 3\\ -6x+2y+5z &= 13\\ 4x+z &= 18 \end{align*}
9) \begin{align*} x+5y+8z &= 19\\ 12x+3y &= 4\\ 3x+4y+9z &= -7 \end{align*}
- Answer
-
\left [ \begin{array}{ccc|c} 1 & 5 & 8 & 16\\ 12 & 3 & 0 & 4\\ 3 & 4 & 9 & -7\end{array} \right ]
10) \begin{align*} 6x+12y+16z &= 4\\ 19x-5y+3z &= -9\\ x+2y &= -8 \end{align*}
For the exercises 11-15, write the linear system from the augmented matrix.
11) \left [ \begin{array}{cc|c} -2 & 5 & 5\\ 6 & -18 & 26\\ \end{array} \right ]
- Answer
-
\begin{align*} -2x+5y &= 5\\ 6x-18y &= 26 \end{align*}
12) \left [ \begin{array}{cc|c} 3 & 4 & 10\\ 10 & 17 & 439\\ \end{array} \right ]
13) \left [ \begin{array}{ccc|c} 3 & 2 & 0 & 3\\ -1 & -9 & 4& -1\\ 8 & 5 & 7 & 8\\ \end{array} \right ]
- Answer
-
\begin{align*} 3x+2y &= 13\\ -x-9y+4z &= 53\\ 8x+5y+7z &= 80 \end{align*}
14) \left [ \begin{array}{ccc|c} 8 & 29 & 1 & 43\\ -1 & 7 & 5 & 38\\ 0 & 0 & 3 & 10\\ \end{array} \right ]
15) \left [ \begin{array}{ccc|c} 4 & 5 & -2 & 12\\ 0 & 1 & 58 & 2\\ 8 & 7 & -3 & -5\\ \end{array} \right ]
- Answer
-
\begin{align*} 4x+5y-2z &= 12\\ y+58z &= 2\\ 8x+7y-3z &= -5 \end{align*}
For the exercises 16-46, solve the system by Gaussian elimination.
16) \left [ \begin{array}{cc|c} 1 & 0 & 3\\ 0 & 0 & 0\\ \end{array} \right ]
17) \left [ \begin{array}{cc|c} 1 & 0 & 1\\ 1 & 0 & 2\\ \end{array} \right ]
- Answer
-
No solutions
18) \left [ \begin{array}{cc|c} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{array} \right ]
19) \left [ \begin{array}{cc|c} -1 & 2 & -3\\ 4 & -5 & 6\\ \end{array} \right ]
- Answer
-
(-1,-2)
20) \left [ \begin{array}{cc|c} -2 & 0 & 1\\ 0 & 2 & -1\\ \end{array} \right ]
21) \begin{align*} 2x-3y &= -9\\ 5x+4y &= 58 \end{align*}
- Answer
-
(6,7)
22) \begin{align*} 6x+2y &= -4\\ 3x+4y &= -17 \end{align*}
23) \begin{align*} 2x+3y &= 12\\ 4x+y &= 14 \end{align*}
- Answer
-
(3,2)
24) \begin{align*} -4x-3y &= -2\\ 3x-5y &= -13 \end{align*}
25) \begin{align*} -5x+8y &= 3\\ 10x+6y &= 5 \end{align*}
- Answer
-
\left (\dfrac{1}{5}, \dfrac{1}{2} \right )
26) \begin{align*} 3x+4y &= 12\\ -6x-8y &= -24 \end{align*}
27) \begin{align*} -60x+45y &= 12\\ 20x-15y &= -4 \end{align*}
- Answer
-
\left (x, \dfrac{4}{15}(5x+1) \right )
28) \begin{align*} 11x+10y &= 43\\ 15x+20y &= 65 \end{align*}
29) \begin{align*} 2x-y &= 2\\ 3x+2y &= 17 \end{align*}
- Answer
-
(3,4)
30) \begin{align*} -1.06x-2.25y &= 5.51\\ -5.03x-1.08y &= 5.40 \end{align*}
31) \begin{align*} \dfrac{3}{4}x-\dfrac{3}{5}y &= 4\\ \dfrac{1}{4}x+\dfrac{2}{3}y &= 1 \end{align*}
- Answer
-
\left (\dfrac{196}{39}, -\dfrac{5}{13} \right )
32) \begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}y &= -1\\ \dfrac{1}{2}x+\dfrac{1}{3}y &= 3 \end{align*}
33) \left [ \begin{array}{ccc|c} 1 & 0 & 0 & 31\\ 0 & 1 & 1 & 45\\ 0 & 0 & 1 & 87\\ \end{array} \right ]
- Answer
-
(31,-42,87)
34) \left [ \begin{array}{ccc|c} 1 & 0 & 1 & 50\\ 1 & 1 & 0 & 20\\ 0 & 1 & 1 & -90\\ \end{array} \right ]
35) \left [ \begin{array}{ccc|c} 1 & 2 & 3 & 4\\ 0 & 5 & 6 & 7\\ 0 & 0 & 8 & 9\\ \end{array} \right ]
- Answer
-
\left (\dfrac{21}{40}, \dfrac{1}{20}, \dfrac{9}{8} \right )
36) \left [ \begin{array}{ccc|c} -0.1 & 0.3 & -0.1 & 0.2\\ -0.4 & 0.2 & 0.1 & 0.8\\ 0.6 & 0.1 & 0.7 & -0.8\\ \end{array} \right ]
37) \begin{align*} -2x+3y-2z &= 3\\ 4x+2y-z &= 9\\ 4x-8y+2z &= -6 \end{align*}
- Answer
-
\left (\dfrac{18}{13}, \dfrac{15}{13}, -\dfrac{15}{13} \right )
38) \begin{align*} x+y-4z &= -4\\ 5x-3y-2z &= 0\\ 2x+6y+7z &= 30 \end{align*}
39) \begin{align*} 2x+3y+2z &= 1\\ -4x-6y-4z &= -2\\ 10x+15y+10z &= 5 \end{align*}
- Answer
-
\left (x, y, \dfrac{1}{2}(1-2x-3y) \right )
40) \begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 5 \end{align*}
41) \begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 3 \end{align*}
- Answer
-
\left (x, -\dfrac{x}{2}, -1 \right )
42) \begin{align*} x+y &= 2\\ x+z &= 1\\ -y-z &= -3 \end{align*}
43) \begin{align*} x+y+z &= 100\\ x+2z &= 125\\ -y+2z &= 25 \end{align*}
- Answer
-
(125,-25,0)
44) \begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}z &= -\dfrac{1}{2}\\ \dfrac{1}{5}x+\dfrac{1}{3}y &= \dfrac{4}{7}\\ \dfrac{1}{5}y-\dfrac{1}{3}z &= \dfrac{2}{9} \end{align*}
45) \begin{align*} -\dfrac{1}{2}x+\dfrac{1}{2}y+\dfrac{1}{7}z &= -\dfrac{53}{14}\\ \dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{1}{4}z &= 3\\ \dfrac{1}{4}x+\dfrac{1}{5}y+\dfrac{1}{3}z &= \dfrac{23}{15} \end{align*}
- Answer
-
(8,1,-2)
46) \begin{align*} -\dfrac{1}{2}x-\dfrac{1}{3}y+\dfrac{1}{4}z &= -\dfrac{29}{6}\\ \dfrac{1}{5}x+\dfrac{1}{6}y-\dfrac{1}{7}z &= \dfrac{431}{210}\\ -\dfrac{1}{8}x+\dfrac{1}{9}y+\dfrac{1}{10}z &= -\dfrac{49}{45} \end{align*}
Extensions
For the exercises 47-51, use Gaussian elimination to solve the system.
47) \begin{align*} \dfrac{x-1}{7}+\dfrac{y-2}{8}+\dfrac{z-3}{4} &= 0\\ x+y+z &= 6\\ \dfrac{x+2}{3}+2y+\dfrac{z-3}{3} &= 5 \end{align*}
- Answer
-
(1,2,3)
48) \begin{align*} \dfrac{x-1}{4}-\dfrac{y+1}{4}+3z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+7}{4}-z &= 4\\ x+y-\dfrac{z-2}{2} &= 1 \end{align*}
49) \begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 8\\ x+y+z &= 1 \end{align*}
- Answer
-
\left (x, \dfrac{31}{28}-\dfrac{3x}{4}, \dfrac{1}{28}(-7x-3) \right )
50) \begin{align*} \dfrac{x-3}{10}+\dfrac{y+3}{2}-2z &= 3\\ \dfrac{x+5}{4}-\dfrac{y-1}{8}+z &= \dfrac{3}{2}\\ \dfrac{x-1}{4}+\dfrac{y+4}{2}+3z &= \dfrac{3}{2} \end{align*}
51) \begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 7\\ x+y+z &= 1 \end{align*}
- Answer
-
No solutions exist.
Real-World Applications
For the exercises 52-61, set up the augmented matrix that describes the situation, and solve for the desired solution.
52) Every day, a cupcake store sells 5,000 cupcakes in chocolate and vanilla flavors. If the chocolate flavor is 3 times as popular as the vanilla flavor, how many of each cupcake sell per day?
53) At a competing cupcake store, \$4,520 worth of cupcakes are sold daily. The chocolate cupcakes cost \$2.25 and the red velvet cupcakes cost \$1.75. If the total number of cupcakes sold per day is 2,200, how many of each flavor are sold each day?
- Answer
-
860 red velvet, 1,340 chocolate
54) You invested \$10,000 into two accounts: one that has simple 3\% interest, the other with 2.5\% interest. If your total interest payment after one year was \$283.50, how much was in each account after the year passed?
55) You invested \$2,300 into account 1, and \$2,700 into account 2. If the total amount of interest after one year is \$254, and account 2 has 1.5 times the interest rate of account 1, what are the interest rates? Assume simple interest rates.
- Answer
-
4\% for account 1, 6\% for account 2
56) Bikes’R’Us manufactures bikes, which sell for \$250. It costs the manufacturer \$180 per bike, plus a startup fee of \$3,500. After how many bikes sold will the manufacturer break even?
57) A major appliance store is considering purchasing vacuums from a small manufacturer. The store would be able to purchase the vacuums for \$86 each, with a delivery fee of \$9,200, regardless of how many vacuums are sold. If the store needs to start seeing a profit after 230 units are sold, how much should they charge for the vacuums?
- Answer
-
\$126
58) The three most popular ice cream flavors are chocolate, strawberry, and vanilla, comprising 83\% of the flavors sold at an ice cream shop. If vanilla sells 1\% more than twice strawberry, and chocolate sells 11\% more than vanilla, how much of the total ice cream consumption are the vanilla, chocolate, and strawberry flavors?
59) At an ice cream shop, three flavors are increasing in demand. Last year, banana, pumpkin, and rocky road ice cream made up 12\% of total ice cream sales. This year, the same three ice creams made up 16.9\% of ice cream sales. The rocky road sales doubled, the banana sales increased by 50\%, and the pumpkin sales increased by 20\%. If the rocky road ice cream had one less percent of sales than the banana ice cream, find out the percentage of ice cream sales each individual ice cream made last year.
- Answer
-
Banana was 3\%, pumpkin was 7\%, and rocky road was 2\%
60) A bag of mixed nuts contains cashews, pistachios, and almonds. There are 1,000 total nuts in the bag, and there are 100 less almonds than pistachios. The cashews weigh 3 g, pistachios weigh 4 g, and almonds weigh 5 g. If the bag weighs 3.7 kg, find out how many of each type of nut is in the bag.
61) A bag of mixed nuts contains cashews, pistachios, and almonds. Originally there were 900 nuts in the bag. 30\% of the almonds, 20\% of the cashews, and 10\% of the pistachios were eaten, and now there are 770 nuts left in the bag. Originally, there were 100 more cashews than almonds. Figure out how many of each type of nut was in the bag to begin with.
- Answer
-
100 almonds, 200 cashews, 600 pistachios
9.7: Solving Systems with Inverses
Verbal
1) In a previous section, we showed that matrix multiplication is not commutative, that is, AB\neq BA in most cases. Can you explain why matrix multiplication is commutative for matrix inverses, that is, A^{-1}A=AA^{-1}?
- Answer
-
If A^{-1} is the inverse of A, then AA^{-1}=I,
2) Does every 2\times 2 matrix have an inverse? Explain why or why not. Explain what condition is necessary for an inverse to exist.
3) Can you explain whether a 2\times 2 matrix with an entire row of zeros can have an inverse?
- Answer
-
No, because ad and bc are both 0, so ad-bc=0
,
4) Can a matrix with an entire column of zeros have an inverse? Explain why or why not.
5) Can a matrix with zeros on the diagonal have an inverse? If so, find an example. If not, prove why not. For simplicity, assume a 2\times 2 matrix.
- Answer
-
Yes. Consider the matrix \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}. The inverse is found with the following calculation:
A^{-1} = \dfrac{1}{0(0)-1(1)} \begin{bmatrix} 0 & -1\\ -1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}
Algebraic
In the exercises 6-12, show that matrix A is the inverse of matrix B.
6) A = \begin{bmatrix} 1 & 0\\ -1 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 0\\ 1 & 1 \end{bmatrix}
7) A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}, B = \begin{bmatrix} -2 & 1\\ \frac{3}{2} & -\frac{1}{2} \end{bmatrix}
- Answer
-
AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I
8) A = \begin{bmatrix} 4 & 5\\ 7 & 0 \end{bmatrix}, B = \begin{bmatrix} 0 & \frac{1}{7}\\ \frac{1}{5} & -\frac{4}{35} \end{bmatrix}
9) A = \begin{bmatrix} -2 & \frac{1}{2}\\ 3 & -1 \end{bmatrix}, B = \begin{bmatrix} -2 & -1\\ -6 & -4 \end{bmatrix}
- Answer
-
AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I
10) A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}
11) A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}
- Answer
-
AB = BA = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = I
12) A = \begin{bmatrix} 3 & 8 & 2\\ 1 & 1 & 1\\ 5 & 6 & 12 \end{bmatrix}, B = \dfrac{1}{36}\begin{bmatrix} -6 & 84 & -6\\ 7 & -26 & 1\\ -1 & -22 & 5 \end{bmatrix}
For the exercises 13-26, find the multiplicative inverse of each matrix, if it exists.
13) \begin{bmatrix} 3 & -2\\ 1 & 9 \end{bmatrix}
- Answer
-
\dfrac{1}{29}\begin{bmatrix} 9 & 2\\ -1 & 3 \end{bmatrix}
14) \begin{bmatrix} -2 & 2\\ 3 & 1 \end{bmatrix}
15) \begin{bmatrix} -3 & 7\\ 9 & 2 \end{bmatrix}
- Answer
-
\dfrac{1}{69}\begin{bmatrix} -2 & 7\\ 9 & 3 \end{bmatrix}
16) \begin{bmatrix} -4 & -3\\ -5 & 8 \end{bmatrix}
17) \begin{bmatrix} 1 & 1\\ 2 & 2 \end{bmatrix}
- Answer
-
There is no inverse
18) \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}
19) \begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}
- Answer
-
\dfrac{4}{7}\begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}
20) \begin{bmatrix} 1 & 0 & 6\\ -2 & 1 & 7\\ 3 & 0 & 2 \end{bmatrix}
21) \begin{bmatrix} 0 & 1 & -3\\ 4 & 1 & 0\\ 1 & 0 & 5 \end{bmatrix}
- Answer
-
\dfrac{1}{17}\begin{bmatrix} -5 & 5 & -3\\ 20 & -3 & 12\\ 1 & -1 & 4 \end{bmatrix}
22) \begin{bmatrix} 1 & 2 & -1\\ -3 & 4 & 1\\ -2 & -4 & -5 \end{bmatrix}
23) \begin{bmatrix} 1 & 9 & -3\\ 2 & 5 & 6\\ 4 & -2 & -7 \end{bmatrix}
- Answer
-
\dfrac{1}{209}\begin{bmatrix} 47 & -57 & 69\\ 10 & 19 & -12\\ -24 & 38 & -13 \end{bmatrix}
24) \begin{bmatrix} 1 & -2 & 3\\ -4 & 8 & -12\\ 1 & 4 & 2 \end{bmatrix}
25) \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5}\\ \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \end{bmatrix}
- Answer
-
\begin{bmatrix} 18 & 60 & -168\\ -56 & -140 & 448\\ 40 & 80 & -280 \end{bmatrix}
26) \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}
For the exercises 27-34, solve the system using the inverse of a 2\times 2 matrix.
27) \begin{align*} 5x-6y &= -61\\ 4x+3y &= -2 \end{align*}
- Answer
-
(-5,6)
28) \begin{align*} 8x+4y &= -100\\ 3x-4y &= 1 \end{align*}
29) \begin{align*} 3x-2y &= 6\\ -x+5y &= -2 \end{align*}
- Answer
-
(2,0)
30) \begin{align*} 5x-4y &= -5\\ 4x+y &= 2.3 \end{align*}
31) \begin{align*} -3x-4y &= 9\\ 12x+4y &= -6 \end{align*}
- Answer
-
\left (\dfrac{1}{3}, -\dfrac{5}{2} \right )
32) \begin{align*} -2x+3y &= \dfrac{3}{10}\\ -x+5y &= \dfrac{1}{2} \end{align*}
33) \begin{align*} \dfrac{8}{5}x-\dfrac{4}{5}y &= \dfrac{2}{5}\\ -\dfrac{8}{5}x+\dfrac{1}{5}y &= \dfrac{7}{10} \end{align*}
- Answer
-
\left (-\dfrac{2}{3}, -\dfrac{11}{6} \right )
34) \begin{align*} \dfrac{1}{2}x+\dfrac{1}{5}y &= -\dfrac{1}{4}\\ \dfrac{1}{2}x-\dfrac{3}{5}y &= -\dfrac{9}{4} \end{align*}
For the exercises 35-42, solve a system using the inverse of a 3\times 3 matrix.
35) \begin{align*} 3x-2y+5z &= 21\\ 5x+4y &= 37\\ x-2y-5z &= 5 \end{align*}
- Answer
-
\left (7, \dfrac{1}{2}, \dfrac{1}{5} \right )
36) \begin{align*} 4x+4y+4z &= 40\\ 2x-3y+4z &= -12\\ -x+3y+4z &= 9 \end{align*}
37) \begin{align*} 6x-5y-z &= 31\\ -x+2y+z &= -6\\ 3x+3y+2z &= 13 \end{align*}
- Answer
-
(5,0,-1)
38) \begin{align*} 6x-5y+2z &= -4\\ 2x+5y-z &= 12\\ 2x+5y+z &= 12 \end{align*}
39) \begin{align*} 4x-2y+3z &= -12\\ 2x+2y-9z &= 33\\ 6y-4z &= 1 \end{align*}
- Answer
-
\dfrac{1}{34} \left(-35, -97, -154 \right)
40) \begin{align*} \dfrac{1}{10}x-\dfrac{1}{5}y+4z &= \dfrac{-41}{2}\\ \dfrac{1}{5}x-20y+\dfrac{2}{5}z &= -101\\ \dfrac{3}{10}x+4y-\dfrac{3}{10}z &= 23 \end{align*}
41) \begin{align*} \dfrac{1}{2}x-\dfrac{1}{5}y+\dfrac{1}{5}z &= \dfrac{31}{100}\\ -\dfrac{3}{4}x-\dfrac{1}{4}y+\dfrac{1}{2}z &= \dfrac{7}{40}\\ -\dfrac{4}{5}x-\dfrac{1}{2}y+\dfrac{3}{2}z &= \dfrac{1}{4} \end{align*}
- Answer
-
\dfrac{1}{690} \left(65, -1136, -229 \right)
42) \begin{align*} 0.1x+0.2y+0.3z &= -1.4\\ 0.1x-0.2y+0.3z &= 0.6\\ 0.4y+0.9z &= -2 \end{align*}
Technology
For the exercises 43-46, use a calculator to solve the system of equations with matrix inverses.
43) \begin{align*} 2x-y &= -3\\ -x+2y &= 2.3\\ \end{align*}
- Answer
-
\left (-\dfrac{37}{30}, \dfrac{8}{15} \right )
44) \begin{align*} -\dfrac{1}{2}x-\dfrac{3}{2}y &= -\dfrac{43}{20}\\ \dfrac{5}{2}x+\dfrac{11}{5}y &= \dfrac{31}{4}\\ \end{align*}
45) \begin{align*} 12.3x-2y-2.5z &= 2\\ 36.9x+7y-7.5z &= -7\\ 8y-5z &= -10 \end{align*}
- Answer
-
\left (\dfrac{10}{123}, -1, \dfrac{2}{5} \right )
46) \begin{align*} 0.5x-3y+6z &= -0.8\\ 0.7x-2y &= -0.06\\ 0.5x+4y+5z &= 0 \end{align*}
Extensions
For the exercises 47-51, find the inverse of the given matrix.
47) \begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 1 \end{bmatrix}
- Answer
-
\dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1 & -1\\ 0 & 1 & 1 & -1\\ 0 & -1 & 1 & 1\\ 0 & 1 & -1 & 1 \end{bmatrix}
48) \begin{bmatrix} -1 & 0 & 2 & 5\\ 0 & 0 & 0 & 2\\ 0 & 2 & -1 & 0\\ 1 & -3 & 0 & 1 \end{bmatrix}
49) \begin{bmatrix} 1 & -2 & 3 & 0\\ 0 & 1 & 0 & 2\\ 1 & 4 & -2 & 3\\ -5 & 0 & 1 & 1 \end{bmatrix}
- Answer
-
\dfrac{1}{39}\begin{bmatrix} 3 & 2 & 1 & -7\\ 18 & -53 & 32 & 10\\ 24 & -36 & 21 & 9\\ -9 & 46 & -16 & -5 \end{bmatrix}
50) \begin{bmatrix} 1 & 2 & 0 & 2 & 3\\ 0 & 2 & 1 & 0 & 0\\ 0 & 0 & 3 & 0 & 1\\ 0 & 2 & 0 & 0 & 1\\ 0 & 0 & 1 & 2 & 0 \end{bmatrix}
51) \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}
- Answer
-
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ -1 & -1 & -1 & -1 & -1 & 1 \end{bmatrix}
Real-World Applications
For the exercises 52-61, write a system of equations that represents the situation. Then, solve the system using the inverse of a matrix.
52) 2,400 tickets were sold for a basketball game. If the prices for floor 1 and floor 2 were different, and the total amount of money brought in is \$64,000, how much was the price of each ticket?
53) In the previous exercise, if you were told there were 400 more tickets sold for floor 2 than floor 1, how much was the price of each ticket?
- Answer
-
Infinite solutions.
54) A food drive collected two different types of canned goods, green beans and kidney beans. The total number of collected cans was 350 and the total weight of all donated food was 348 lb, 12 oz. If the green bean cans weigh 2 oz less than the kidney bean cans, how many of each can was donated?
55) Students were asked to bring their favorite fruit to class. 95\% of the fruits consisted of banana, apple, and oranges. If oranges were twice as popular as bananas, and apples were 5\% less popular than bananas, what are the percentages of each individual fruit?
- Answer
-
50\% oranges, 25\% bananas, 20\% apples
56) A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at \$1 and the chocolate chip cookies at \$0.75. They raised \$700 and sold 850 items. How many brownies and how many cookies were sold?
57) A clothing store needs to order new inventory. It has three different types of hats for sale: straw hats, beanies, and cowboy hats. The straw hat is priced at \$13.99, the beanie at \$7.99, and the cowboy hat at \$14.49. If 100 hats were sold this past quarter, \$1,119 was taken in by sales, and the amount of beanies sold was 10 more than cowboy hats, how many of each should the clothing store order to replace those already sold?
- Answer
-
10 straw hats, 50 beanies, 40 cowboy hats
58) Anna, Ashley, and Andrea weigh a combined 370 lb. If Andrea weighs 20 lb more than Ashley, and Anna weighs 1.5 times as much as Ashley, how much does each girl weigh?
59) Three roommates shared a package of 12 ice cream bars, but no one remembers who ate how many. If Tom ate twice as many ice cream bars as Joe, and Albert ate three less than Tom, how many ice cream bars did each roommate eat?
- Answer
-
Tom ate 6, Joe ate 3, and Albert ate 3.
60) A farmer constructed a chicken coop out of chicken wire, wood, and plywood. The chicken wire cost \$2 per square foot, the wood \$10 per square foot, and the plywood \$5 per square foot. The farmer spent a total of \$51, and the total amount of materials used was 14 ft2. He used 3 ft2 more chicken wire than plywood. How much of each material in did the farmer use?
61) Jay has lemon, orange, and pomegranate trees in his backyard. An orange weighs 8 oz, a lemon 5 oz, and a pomegranate 11 oz. Jay picked 142 pieces of fruit weighing a total of 70 lb, 10 oz. He picked 15.5 times more oranges than pomegranates. How many of each fruit did Jay pick?
- Answer
-
124 oranges, 10 lemons, 8 pomegranates
9.8: Solving Systems with Cramer's Rule
Verbal
1) Explain why we can always evaluate the determinant of a square matrix.
- Answer
-
A determinant is the sum and products of the entries in the matrix, so you can always evaluate that product—even if it does end up being 0.
2) Examining Cramer’s Rule, explain why there is no unique solution to the system when the determinant of your matrix is 0. For simplicity, use a 2\times 2 matrix.
3) Explain what it means in terms of an inverse for a matrix to have a 0 determinant.
- Answer
-
The inverse does not exist.
4) The determinant of 2\times 2 matrix A is 3. If you switch the rows and multiply the first row by 6 and the second row by 2, explain how to find the determinant and provide the answer.
Algebraic
For the exercises 5-24, find the determinant.
5) \begin{vmatrix} 1 & 2\\ 3 & 4 \end{vmatrix}
- Answer
-
-2
6) \begin{vmatrix} -1 & 2\\ 3 & -4 \end{vmatrix}
7) \begin{vmatrix} 2 & -5\\ -1 & 6 \end{vmatrix}
- Answer
-
7
8) \begin{vmatrix} -8 & 4\\ -1 & 5 \end{vmatrix}
9) \begin{vmatrix} 1 & 0\\ 3 & -4 \end{vmatrix}
- Answer
-
-4
10) \begin{vmatrix} 10 & 20\\ 0 & -10 \end{vmatrix}
11) \begin{vmatrix} 10 & 0.2\\ 5 & 0.1 \end{vmatrix}
- Answer
-
0
12) \begin{vmatrix} 6 & -3\\ 8 & 4 \end{vmatrix}
13) \begin{vmatrix} -2 & -3\\ 3.1 & 4,000 \end{vmatrix}
- Answer
-
-7,990.7
14) \begin{vmatrix} -1.1 & 0.6\\ 7.2 & -0.5 \end{vmatrix}
15) \begin{vmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -3 \end{vmatrix}
- Answer
-
3
16) \begin{vmatrix} -1 & 4 & 0\\ 0 & 2 & 3\\ 0 & 0 & -3 \end{vmatrix}
17) \begin{vmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{vmatrix}
- Answer
-
-1
18) \begin{vmatrix} 2 & -3 & 1\\ 3 & -4 & 1\\ -5 & 6 & 1 \end{vmatrix}
19) \begin{vmatrix} -2 & 1 & 4\\ -4 & 2 & -8\\ 2 & -8 & -3 \end{vmatrix}
- Answer
-
224
20) \begin{vmatrix} 6 & -1 & 2\\ -4 & -3 & 5\\ 1 & 9 & -1 \end{vmatrix}
21) \begin{vmatrix} 5 & 1 & -1\\ 2 & 3 & 1\\ 3 & -6 & -3 \end{vmatrix}
- Answer
-
15
22) \begin{vmatrix} 1.1 & 2 & -1\\ -4 & 0 & 0\\ 4.1 & -0.4 & 2.5 \end{vmatrix}
23) \begin{vmatrix} 2 & -1.6 & 3.1\\ 1.1 & 3 & -8\\ -9.3 & 0 & 2 \end{vmatrix}
- Answer
-
-17.03
24) \begin{vmatrix} -\frac{1}{2} & \frac{1}{3} & \frac{1}{4}\\ \frac{1}{5} & -\frac{1}{6} & \frac{1}{7}\\ 0 & 0 & \frac{1}{8} \end{vmatrix}
For the exercises 25-34, solve the system of linear equations using Cramer’s Rule.
25) \begin{align*} 2x-3y &= -1\\ 4x+5y &= 9 \end{align*}
- Answer
-
(1,1)
26) \begin{align*} 5x-4y &= 2\\ -4x+7y &= 6 \end{align*}
27) \begin{align*} 6x-3y &= 2\\ -8x+9y &= -1 \end{align*}
- Answer
-
\left (\dfrac{1}{2}, \dfrac{1}{3} \right )
28) \begin{align*} 2x+6y &= 12\\ 5x-2y &= 13 \end{align*}
29) \begin{align*} 4x+3y &= 23\\ 2x-y &= -1 \end{align*}
- Answer
-
(2,5)
30) \begin{align*} 10x-6y &= 2\\ -5x+8y &= -1 \end{align*}
31) \begin{align*} 4x-3y &= -3\\ 2x+6y &= -4 \end{align*}
- Answer
-
\left (-1, -\dfrac{1}{3} \right )
32) \begin{align*} 4x-5y &= 7\\ -3x+9y &= 0 \end{align*}
33) \begin{align*} 4x+10y &= 180\\ -3x-5y &= -105 \end{align*}
- Answer
-
(15,12)
34) \begin{align*} 8x-2y &= -3\\ -4x+6y &= 4 \end{align*}
For the exercises 35-44, solve the system of linear equations using Cramer’s Rule.
35) \begin{align*} x+2y-4z &= -1\\ 7x+3y+5z &= 26\\ -2x-6y+7z &= -6 \end{align*}
- Answer
-
(1,3,2)
36) \begin{align*} -5x+2y-4z &= -47\\ 4x-3y-z &= -94\\ 3x-3y+2z &= 94 \end{align*}
37) \begin{align*} 4x+5y-z &= -7\\ -2x-9y+2z &= 8\\ 5y+7z &= 21 \end{align*}
- Answer
-
(-1,0,3)
38) \begin{align*} 4x-3y+4z &= 10\\ 5x-2z &= -2\\ 3x+2y-5z &= -9 \end{align*}
39) \begin{align*} 4x-2y+3z &= 6\\ -6x+y &= -2\\ 2x+7y+8z &= 24 \end{align*}
- Answer
-
\left (\dfrac{1}{2}, 1, 2 \right )
40) \begin{align*} 5x+2y-z &= 1\\ -7x-8y+3z &= 1.5\\ 6x-12y+z &= 7 \end{align*}
41) \begin{align*} 13x-17y+16z &= 73\\ -11x+15y+17z &= 61\\ 46x+10y-30z &= -18 \end{align*}
- Answer
-
(2,1,4)
42) \begin{align*} -4x-3y-8z &= -7\\ 2x-9y+5z &= 0.5\\ 5x-6y-5z &= -2 \end{align*}
43) \begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ x+y+z &= 1 \end{align*}
- Answer
-
Infinite solutions
44) \begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ 12x+18y-24z &= -30 \end{align*}
Technology
For the exercises 45-48, use the determinant function on a graphing utility.
45) \begin{vmatrix} 1 & 0 & 8 & 9\\ 0 & 2 & 1 & 0\\ 1 & 0 & 3 & 0\\ 0 & 2 & 4 & 3 \end{vmatrix}
- Answer
-
24
46) \begin{vmatrix} 1 & 0 & 2 & 1\\ 0 & -9 & 1 & 3\\ 3 & 0 & -2 & -1\\ 0 & 1 & 1 & -2 \end{vmatrix}
47) \begin{vmatrix} \frac{1}{2} & 1 & 7 & 4\\ 0 & \frac{1}{2} & 100 & 5\\ 0 & 0 & 2 & 2,000\\ 0 & 0 & 0 & 2 \end{vmatrix}
- Answer
-
1
48) \begin{vmatrix} 1 & 0 & 0 & 0\\ 2 & 3 & 0 & 0\\ 4 & 5 & 6 & 0\\ 7 & 8 & 9 & 0 \end{vmatrix}
Real-World Applications
For the exercises 49-52, create a system of linear equations to describe the behavior. Then, calculate the determinant. Will there be a unique solution? If so, find the unique solution.
49) Two numbers add up to 56. One number is 20 less than the other.
- Answer
-
Yes; 18, 38
50) Two numbers add up to 104. If you add two times the first number plus two times the second number, your total is 208
51) Three numbers add up to 106. The first number is 3 less than the second number. The third number is 4 more than the first number.
- Answer
-
Yes; 33, 36, 37
52) Three numbers add to 216. The sum of the first two numbers is 112. The third number is 8 less than the first two numbers combined.
For the exercises 53-65, create a system of linear equations to describe the behavior. Then, solve the system for all solutions using Cramer’s Rule.
53) You invest \$10,000 into two accounts, which receive 8\% interest and 5\% interest. At the end of a year, you had \$10,710 in your combined accounts. How much was invested in each account?
- Answer
-
\$7,000 in first account, \$3,000 in second account.
54) You invest \$80,000 into two accounts, \$22,000 in one account, and \$58,000 in the other account. At the end of one year, assuming simple interest, you have earned \$2,470 in interest. The second account receives half a percent less than twice the interest on the first account. What are the interest rates for your accounts?
55) A movie theater needs to know how many adult tickets and children tickets were sold out of the 1,200 total tickets. If children’s tickets are \$5.95, adult tickets are \$11.15, and the total amount of revenue was \$12,756, how many children’s tickets and adult tickets were sold?
- Answer
-
120 children, 1,080 adult
56) A concert venue sells single tickets for \$40 each and couple’s tickets for \$65. If the total revenue was \$18,090 and the 321 tickets were sold, how many single tickets and how many couple’s tickets were sold?
57) You decide to paint your kitchen green. You create the color of paint by mixing yellow and blue paints. You cannot remember how many gallons of each color went into your mix, but you know there were 10 gal total. Additionally, you kept your receipt, and know the total amount spent was \$29.50. If each gallon of yellow costs \$2.59, and each gallon of blue costs \$3.19, how many gallons of each color go into your green mix?
- Answer
-
4 gal yellow, 6 gal blue
58) You sold two types of scarves at a farmers’ market and would like to know which one was more popular. The total number of scarves sold was 56, the yellow scarf cost \$10, and the purple scarf cost \$11. If you had total revenue of \$583, how many yellow scarves and how many purple scarves were sold?
59) Your garden produced two types of tomatoes, one green and one red. The red weigh 10 oz, and the green weigh 4 oz. You have 30 tomatoes, and a total weight of 13 lb, 14 oz. How many of each type of tomato do you have?
- Answer
-
13 green tomatoes, 17 red tomatoes
60) At a market, the three most popular vegetables make up 53\% of vegetable sales. Corn has 4\% higher sales than broccoli, which has 5\% more sales than onions. What percentage does each vegetable have in the market share?
61) At the same market, the three most popular fruits make up 37\% of the total fruit sold. Strawberries sell twice as much as oranges, and kiwis sell one more percentage point than oranges. For each fruit, find the percentage of total fruit sold.
- Answer
-
Strawberries 18\%, oranges 9\%, kiwi 10\%
62) Three bands performed at a concert venue. The first band charged \$15 per ticket, the second band charged \$45 per ticket, and the final band charged \$22 per ticket. There were 510 tickets sold, for a total of \$12,700. If the first band had 40 more audience members than the second band, how many tickets were sold for each band?
63) A movie theatre sold tickets to three movies. The tickets to the first movie were \$5, the tickets to the second movie were \$11, and the third movie was \$12. 100 tickets were sold to the first movie. The total number of tickets sold was 642, for a total revenue of \$6,774. How many tickets for each movie were sold?
- Answer
-
100 for movie 1, 230 for movie 2, 312 for movie 3
64) Men aged 20–29, 30–39, and 40–49 made up 78\% of the population at a prison last year. This year, the same age groups made up 82.08\% of the population. The 20–29 age group increased by 20%, the 30–39 age group increased by 2\%, and the 40–49 age group decreased to \dfrac{3}{4} of their previous population. Originally, the 30–39 age group had 2\% more prisoners than the 20–29 age group. Determine the prison population percentage for each age group last year.
65) At a women’s prison down the road, the total number of inmates aged 20–49 totaled 5,525. This year, the 20–29 age group increased by 10\%, the 30–39 age group decreased by 20\%, and the 40–49 age group doubled. There are now 6,040 prisoners. Originally, there were 500 more in the 30–39 age group than the 20–29 age group. Determine the prison population for each age group last year.
- Answer
-
20–29: 2,100, 30–39: 2,600, 40–49: 825
For the exercises 66-68, use this scenario: A health-conscious company decides to make a trail mix out of almonds, dried cranberries, and chocolate-covered cashews. The nutritional information for these items is shown in the Table below.
| Fat (g) | Protein (g) | Carbohydrates (g) | |
|---|---|---|---|
| Almonds (10) | 6 | 2 | 3 |
| Cranberries (10) | 0.02 | 0 | 8 |
| Cashews (10) | 7 | 3.5 | 5.5 |
66) For the special “low-carb”trail mix, there are 1,000 pieces of mix. The total number of carbohydrates is 425 g, and the total amount of fat is 570.2 g. If there are 200 more pieces of cashews than cranberries, how many of each item is in the trail mix?
67) For the “hiking” mix, there are 1,000 pieces in the mix, containing 390.8 g of fat, and 165 g of protein. If there is the same amount of almonds as cashews, how many of each item is in the trail mix?
- Answer
-
300 almonds, 400 cranberries, 300 cashews
68) For the “energy-booster” mix, there are 1,000 pieces in the mix, containing 145 g of protein and 625 g of carbohydrates. If the number of almonds and cashews summed together is equivalent to the amount of cranberries, how many of each item is in the trail mix?
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


