15.3E: Conservative Vector Fields (Exercises)
- Last updated
- Jan 25, 2020
- Save as PDF
- Page ID
- 35135
( \newcommand{\kernel}{\mathrm{null}\,}\)
1. True or False? If vector field ⇀F is conservative on the open and connected region D, then line integrals of ⇀F are path independent on D, regardless of the shape of D.
- Answer
- True
2. True or False? Function ⇀r(t)=⇀a+t(⇀b−⇀a), where 0≤t≤1, parameterizes the straight-line segment from ⇀a to ⇀b.
- Answer
- True
3. True or False? Vector field ⇀F(x,y,z)=(ysinz)ˆi+(xsinz)ˆj+(xycosz)ˆk is conservative.
- Answer
- True
4. True or False? Vector field ⇀F(x,y,z)=yˆi+(x+z)ˆj−yˆk is conservative.
5. Justify the Fundamental Theorem of Line Integrals for ∫C⇀F·d⇀r in the case when ⇀F(x,y)=(2x+2y)ˆi+(2x+2y)ˆj and C is a portion of the positively oriented circle x2+y2=25 from (5,0) to (3,4).
- Answer
- ∫C⇀F·d⇀r=24 units of work
6. [T] Find ∫C⇀F·d⇀r, where ⇀F(x,y)=(yexy+cosx)ˆi+(xexy+1y2+1)ˆj and C is a portion of curve y=sinx from x=0 to x=π2.
7. [T] Evaluate line integral ∫C⇀F·d⇀r, where ⇀F(x,y)=(exsiny−y)ˆi+(excosy−x−2)ˆj, and C is the path given by ⇀r(t)=(t3sinπt2)ˆi−(π2cos(πt2+π2))ˆj for 0≤t≤1.
- Answer
- ∫C⇀F·d⇀r=(e−3π2) units of work
For the following exercises, determine whether the vector field is conservative and, if it is, find the potential function.
8. ⇀F(x,y)=2xy3ˆi+3y2x2ˆj
9. ⇀F(x,y)=(−y+exsiny)ˆi+((x+2)excosy)ˆj
- Answer
- Not conservative
10. ⇀F(x,y)=(e2xsiny)ˆi+(e2xcosy)ˆj
11. ⇀F(x,y)=(6x+5y)ˆi+(5x+4y)ˆj
- Answer
- Conservative, f(x,y)=3x2+5xy+2y2+k
12. ⇀F(x,y)=(2xcos(y)−ycos(x))ˆi+(−x2sin(y)−sin(x))ˆj
13. ⇀F(x,y)=(yex+sin(y))ˆi+(ex+xcos(y))ˆj
- Answer
- Conservative, f(x,y)=yex+xsin(y)+k
For the following exercises, evaluate the line integrals using the Fundamental Theorem of Line Integrals.
14. ∮C(yˆi+xˆj)·d⇀r, where C is any path from (0,0) to (2,4)
15. ∮C(2ydx+2xdy), where C is the line segment from (0,0) to (4,4)
- Answer
- ∮C(2ydx+2xdy)=32 units of work
16. [T] ∮C[arctanyx−xyx2+y2]dx+[x2x2+y2+e−y(1−y)]dy, where C is any smooth curve from (1,1) to (−1,2).
17. Find the conservative vector field for the potential function f(x,y)=5x2+3xy+10y2.
- Answer
- ⇀F(x,y)=(10x+3y)ˆi+(3x+20y)ˆj
For the following exercises, determine whether the vector field is conservative and, if so, find a potential function.
18. ⇀F(x,y)=(12xy)ˆi+6(x2+y2)ˆj
19. ⇀F(x,y)=(excosy)ˆi+6(exsiny)ˆj
- Answer
- ⇀F is not conservative.
20. ⇀F(x,y)=(2xyex2y)ˆi+6(x2ex2y)ˆj
21. ⇀F(x,y,z)=(yez)ˆi+(xez)ˆj+(xyez)ˆk
- Answer
- ⇀F is conservative and a potential function is f(x,y,z)=xyez+k.
22. ⇀F(x,y,z)=(siny)ˆi−(xcosy)ˆj+ˆk
23. ⇀F(x,y,z)=1yˆi−xy2ˆj+(2z−1)ˆk
- Answer
- ⇀F is conservative and a potential function is f(x,y,z)=xy+z2−z+k.
24. ⇀F(x,y,z)=3z2ˆi−cosyˆj+2xzˆk
25. ⇀F(x,y,z)=(2xy)ˆi+(x2+2yz)ˆj+y2ˆk
- Answer
- ⇀F is conservative and a potential function is f(x,y,z)=x2y+y2z+k.
For the following exercises, determine whether the given vector field is conservative and find a potential function.
26. ⇀F(x,y)=(excosy)ˆi+6(exsiny)ˆj
27. ⇀F(x,y)=(2xyex2y)ˆi+(x2ex2y)ˆj
- Answer
- ⇀F is conservative and a potential function is f(x,y)=ex2y+k
For the following exercises, evaluate the integral using the Fundamental Theorem of Line Integrals.
28. Evaluate ∫C⇀∇f·d⇀r, where f(x,y,z)=cos(πx)+sin(πy)−xyz and C is any path that starts at (1,12,2) and ends at (2,1,−1).
29. [T] Evaluate ∫C⇀∇f·d⇀r, where f(x,y)=xy+ex and C is a straight line from (0,0) to (2,1).
- Answer
- ∫C⇀F·d⇀r=(e2+1) units of work
30. [T] Evaluate ∫C⇀∇f·d⇀r, where f(x,y)=x2y−x and C is any path in a plane from (1, 2) to (3, 2).
31. Evaluate ∫C⇀∇f·d⇀r, where f(x,y,z)=xyz2−yz and C has initial point (1,2,3) and terminal point (3,5,2).
- Answer
- ∫C⇀F·d⇀r=38 units of work
For the following exercises, let ⇀F(x,y)=2xy2ˆi+(2yx2+2y)ˆj and G(x,y)=(y+x)ˆi+(y−x)ˆj, and let C1 be the curve consisting of the circle of radius 2, centered at the origin and oriented counterclockwise, and C2 be the curve consisting of a line segment from (0,0) to (1,1) followed by a line segment from (1,1) to (3,1).
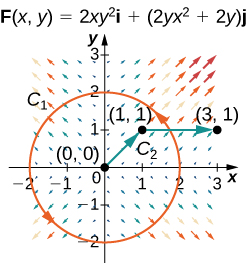
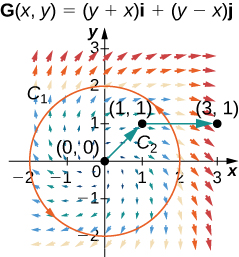
32. Calculate the line integral of ⇀F over C1.
33. Calculate the line integral of ⇀G over C1.
- Answer
- ∮C1⇀G·d⇀r=−8π units of work
34. Calculate the line integral of ⇀F over C2.
35. Calculate the line integral of ⇀G over C2.
- Answer
- ∮C2⇀F·d⇀r=7 units of work
36. [T] Let ⇀F(x,y,z)=x2ˆi+zsin(yz)ˆj+ysin(yz)ˆk. Calculate ∮C⇀F·d⇀r, where C is a path from A=(0,0,1) to B=(3,1,2).
37. [T] Find line integral \displaystyle ∮_C\vecs F·dr of vector field \vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k} along curve C parameterized by \vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+t\cos(πt),1≤t≤4.
- Answer
- \displaystyle \int _C\vecs F·d\vecs r=159 units of work
For exercises 38 - 40, show that the following vector fields are conservative. Then calculate \displaystyle \int _C\vecs F·d\vecs r for the given curve.
38. \vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}; C is the curve consisting of line segments from (1,1) to (0,2) to (3,0).
39. \vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}; C is parameterized by x=t^3−1,\;y=t^6−t, for 0≤t≤1.
- Answer
- \displaystyle \int _C\vecs F·d\vecs r=−1 units of work
40. [T] \vecs{F}(x,y)=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}; C is the curve \langle e^t,e^{t+1}\rangle, for −1≤t≤0.
41. The mass of Earth is approximately 6×10^{27}g and that of the Sun is 330,000 times as much. The gravitational constant is 6.7×10^{−8}cm^3/s^2·g. The distance of Earth from the Sun is about 1.5×10^{12}cm. Compute, approximately, the work necessary to increase the distance of Earth from the Sun by 1\;cm.
- Answer
- 4×10^{31} erg
42. [T] Let \vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}. Evaluate the integral \displaystyle \int _C\vecs F·d\vecs r, where \vecs r(t)=\langle\sqrt{t},t^3,e^{\sqrt{t}}\rangle, for 0≤t≤1.
43. [T] Let C:[1,2]→ℝ^2 be given by x=e^{t−1},y=\sin\left(\frac{π}{t}\right). Use a computer to compute the integral \displaystyle \int _C\vecs F·d\vecs r=\int _C 2x\cos y\,dx−x^2\sin y\,dy, where \vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.
- Answer
- \displaystyle \int _C\vecs F·d\vecs s=0.4687 units of work
44. [T] Use a computer algebra system to find the mass of a wire that lies along the curve \vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k}, where 0≤t≤1, if the density is given by d(t) = \dfrac{3}{2}t.
45. Find the circulation and flux of field \vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j} around and across the closed semicircular path that consists of semicircular arch \vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π, followed by line segment \vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.
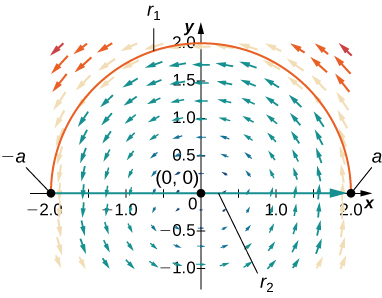
- Answer
- \text{circulation}=πa^2 and \text{flux}=0
46. Compute \displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy, where \vecs r(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.
47. Complete the proof of the theorem titled THE PATH INDEPENDENCE TEST FOR CONSERVATIVE FIELDS by showing that f_y=Q(x,y).
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


