15.5E: Divergence and Curl (Exercises)
- Page ID
- 35139
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For the following exercises, determine whether the statement is True or False.
1. If the coordinate functions of \(\vecs F : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) have continuous second partial derivatives, then \(\text{curl} \, (\text{div} \,\vecs F)\) equals zero.
2. \(\vecs\nabla \cdot (x \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z \,\mathbf{\hat k} ) = 1\).
- Answer
- False
3. All vector fields of the form \(\vecs F(x,y,z) = f(x)\,\mathbf{\hat i} + g(y)\,\mathbf{\hat j} + h(z)\,\mathbf{\hat k}\) are conservative.
4. If \(\text{curl} \, \vecs F = \vecs 0\), then \(\vecs F\) is conservative.
- Answer
- True
5. If \(\vecs F\) is a constant vector field then \(\text{div} \,\vecs F = 0\).
6. If \(\vecs F\) is a constant vector field then \(\text{curl} \,\vecs F =\vecs 0\).
- Answer
- True
For the following exercises, find the curl of \(\vecs F\).
7. \(\vecs F(x,y,z) = xy^2z^4\,\mathbf{\hat i} + (2x^2y + z)\,\mathbf{\hat j} + y^3 z^2\,\mathbf{\hat k}\)
8. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x\,\mathbf{\hat j} + (y + 2z)\,\mathbf{\hat k}\)
- Answer
- \(\text{curl} \,\vecs F = \,\mathbf{\hat i} + x^2\,\mathbf{\hat j} + y^2\,\mathbf{\hat k}\)
9. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z\,\mathbf{\hat j} + xe^{2z}\,\mathbf{\hat k}\)
10. \(\vecs F(x,y,z) = x^2 yz\,\mathbf{\hat i} + xy^2 z\,\mathbf{\hat j} + xyz^2\,\mathbf{\hat k}\)
- Answer
- \(\text{curl} \, \vecs F = (xz^2 - xy^2)\,\mathbf{\hat i} + (x^2 y - yz^2)\,\mathbf{\hat j} + (y^2z - x^2z)\,\mathbf{\hat k}\)
11. \(\vecs F(x,y,z) = (x \, \cos y)\,\mathbf{\hat i} + xy^2\,\mathbf{\hat j}\)
12. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z)\,\mathbf{\hat j} + (z - x)\,\mathbf{\hat k}\)
- Answer
- \(\text{curl }\, \vecs F = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\)
13. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2 \,\mathbf{\hat j} + y^2z^3 \,\mathbf{\hat k}\)
14. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz \,\mathbf{\hat j} + xz \,\mathbf{\hat k}\)
- Answer
- \(\text{curl }\, \vecs F = - y\,\mathbf{\hat i} - z \,\mathbf{\hat j} - x \,\mathbf{\hat k}\)
15. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)
16. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\) for constants \(a, \,b, \,c\).
- Answer
- \(\text{curl }\, \vecs F = \vecs 0\)
For the following exercises, find the divergence of \(\vecs F\).
17. \(\vecs F(x,y,z) = x^2 z\,\mathbf{\hat i} + y^2 x \,\mathbf{\hat j} + (y + 2z) \,\mathbf{\hat k}\)
18. \(\vecs F(x,y,z) = 3xyz^2\,\mathbf{\hat i} + y^2 \sin z \,\mathbf{\hat j} + xe^2z \,\mathbf{\hat k}\)
- Answer
- \(\text{div}\,\vecs F = 3yz^2 + 2y \, \sin z + 2xe^{2z}\)
19. \(\vecs{F}(x,y) = (\sin x)\,\mathbf{\hat i} + (\cos y) \,\mathbf{\hat j}\)
20. \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\)
- Answer
- \(\text{div}\,\vecs F = 2(x + y + z)\)
21. \(\vecs F(x,y,z) = (x - y)\,\mathbf{\hat i} + (y - z) \,\mathbf{\hat j} + (z - x) \,\mathbf{\hat k}\)
22. \(\vecs{F}(x,y) = \dfrac{x}{\sqrt{x^2+y^2}}\,\mathbf{\hat i} + \dfrac{y}{\sqrt{x^2+y^2}}\,\mathbf{\hat j}\)
- Answer
- \(\text{div}\,\vecs F = \dfrac{1}{\sqrt{x^2+y^2}}\)
23. \(\vecs{F}(x,y) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j}\)
24. \(\vecs F(x,y,z) = ax\,\mathbf{\hat i} + by \,\mathbf{\hat j} + c \,\mathbf{\hat k}\) for constants \(a, \,b, \,c\).
- Answer
- \(\text{div}\,\vecs F = a + b\)
25. \(\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + x^2y^2z^2\,\mathbf{\hat j} + y^2z^3\,\mathbf{\hat k}\)
26. \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} + yz\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\)
- Answer
- \(\text{div}\,\vecs F = x + y + z\)
For exercises 27 & 28, determine whether each of the given scalar functions is harmonic.
27. \(u(x,y,z) = e^{-x} (\cos y - \sin y)\)
28. \(w(x,y,z) = (x^2 + y^2 + z^2)^{-1/2}\)
- Answer
- Harmonic
29. If \(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) and \(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), find \(\text{curl} \, (\vecs F \times \vecs G)\).
30. If \(\vecs F(x,y,z) = 2\,\mathbf{\hat i} + 2x j + 3y k\) and \(\vecs G(x,y,z) = x\,\mathbf{\hat i} - y \,\mathbf{\hat j} + z \,\mathbf{\hat k}\), find \(\text{div} \, (\vecs F \times \vecs G)\).
- Answer
- \(\text{div} \, (\vecs F \times \vecs G) = 2z + 3x\)
31. Find \(\text{div} \,\vecs F\), given that \(\vecs F = \vecs \nabla f\), where \(f(x,y,z) = xy^3z^2\).
32. Find the divergence of \(\vecs F\) for vector field \(\vecs F(x,y,z) = (y^2 + z^2) (x + y) \,\mathbf{\hat i} + (z^2 + x^2)(y + z) \,\mathbf{\hat j} + (x^2 + y^2)(z + x) \,\mathbf{\hat k}\).
- Answer
- \(\text{div}\,\vecs F = 2r^2\)
33. Find the divergence of \(\vecs F\) for vector field \(\vecs F(x,y,z) = f_1(y,z)\,\mathbf{\hat i} + f_2 (x,z) \,\mathbf{\hat j} + f_3 (x,y) \,\mathbf{\hat k}\).
For exercises 34 - 36, use \(r = |\vecs r|\) and \(\vecs r(x,y,z) = \langle x,y,z\rangle\).
34. Find the \(\text{curl} \, \vecs r\)
- Answer
- \(\text{curl} \, \vecs r = \vecs 0\)
35. Find the \(\text{curl}\, \dfrac{\vecs r}{r}\).
36. Find the \(\text{curl}\, \dfrac{\vecs r}{r^3}\).
- Answer
- \(\text{curl}\, \dfrac{\vecs r}{r^3} = \vecs 0\)
37. Let \(\vecs{F}(x,y) = \dfrac{-y\,\mathbf{\hat i}+x\,\mathbf{\hat j}}{x^2+y^2}\), where \(\vecs F\) is defined on \(\big\{(x,y) \in \mathbb{R} | (x,y) \neq (0,0) \big\}\). Find \(\text{curl}\, \vecs F\).
For the following exercises, use a computer algebra system to find the curl of the given vector fields.
38. [T] \(\vecs F(x,y,z) = \arctan \left(\dfrac{x}{y}\right)\,\mathbf{\hat i} + \ln \sqrt{x^2 + y^2} \,\mathbf{\hat j}+ \,\mathbf{\hat k}\)
- Answer
- \(\text{curl }\, \vecs F = \dfrac{2x}{x^2+y^2}\,\mathbf{\hat k}\)
39. [T] \(\vecs F(x,y,z) = \sin (x - y)\,\mathbf{\hat i} + \sin (y - z) \,\mathbf{\hat j} + \sin (z - x) \,\mathbf{\hat k}\)
For the following exercises, find the divergence of \(\vecs F\) at the given point.
40. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\) at \((2, -1, 3)\)
- Answer
- \(\text{div}\,\vecs F = 0\)
41. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) at \((1, 2, 3)\)
42. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\) at \((3, 2, 0)\)
- Answer
- \(\text{div}\,\vecs F = 2 - 2e^{-6}\)
43. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) at \((1, 2, 1)\)
44. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \) at \((0, 0, 3)\)
- Answer
- \(\text{div}\,\vecs F = 0\)
For exercises 45- 49, find the curl of \(\vecs F\) at the given point.
45. \(\vecs F(x,y,z) = \,\mathbf{\hat i} + \,\mathbf{\hat j} + \,\mathbf{\hat k}\) at \((2, -1, 3)\)
46. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + x\,\mathbf{\hat k}\) at \((1, 2, 3)\)
- Answer
- \(\text{curl }\, \vecs F = \mathbf{\hat j} - 3\,\mathbf{\hat k}\)
47. \(\vecs F(x,y,z) = e^{-xy}\,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + e^{yz}\,\mathbf{\hat k}\) at \((3, 2, 0)\)
48. \(\vecs F(x,y,z) = xyz \,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) at \((1, 2, 1)\)
- Answer
- \(\text{curl }\, \vecs F = 2\,\mathbf{\hat j} - \,\mathbf{\hat k}\)
49. \(\vecs F(x,y,z) = e^x \sin y \,\mathbf{\hat i} - e^x \cos y\,\mathbf{\hat j} \) at \((0, 0, 3)\)
50. Let \(\vecs F(x,y,z) = (3x^2 y + az) \,\mathbf{\hat i} + x^3\,\mathbf{\hat j} + (3x + 3z^2)\,\mathbf{\hat k}\). For what value of \(a\) is \(\vecs F\) conservative?
- Answer
- \(a = 3\)
51. Given vector field \(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle -y,x\rangle\) on domain \(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}} = \big\{(x,y) \in \mathbb{R}^2 |(x,y) \neq (0,0) \big\}\), is \(\vecs F\) conservative?
52. Given vector field \(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} \langle x,y\rangle\) on domain \(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}}\), is \(\vecs F\) conservative?
- Answer
- \(\vecs F\) is conservative.
53. Find the work done by force field \(\vecs{F}(x,y) = e^{-y}\,\mathbf{\hat i} - xe^{-y}\,\mathbf{\hat j}\) in moving an object from\(P(0, 1)\) to \(Q(2, 0)\). Is the force field conservative?
54. Compute divergence \(\vecs F(x,y,z) = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\).
- Answer
- \(\text{div}\,\vecs F = \cosh x + \sinh y - xy\)
55. Compute \(\text{curl }\, \vecs F = (\sinh x)\,\mathbf{\hat i} + (\cosh y)\,\mathbf{\hat j} - xyz\,\mathbf{\hat k}\).
For the following exercises, consider a rigid body that is rotating about the \(x\)-axis counterclockwise with constant angular velocity \(\vecs \omega = \langle a,b,c \rangle\). If \(P\) is a point in the body located at \(\vecs r = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\), the velocity at \(P\) is given by vector field \(\vecs F = \vecs \omega \times \vecs r\).
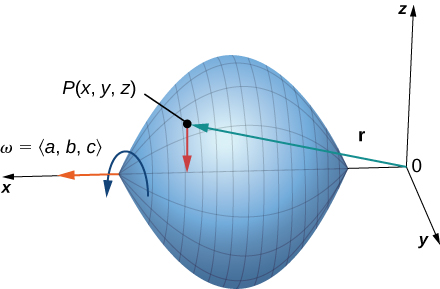
56. Express \(\vecs F\) in terms of \(\,\mathbf{\hat i},\;\,\mathbf{\hat j},\) and \(\,\mathbf{\hat k}\) vectors.
- Answer
- \(\vecs F = (bz - cy)\,\mathbf{\hat i}+(cx - az)\,\mathbf{\hat j} + (ay - bx)\,\mathbf{\hat k}\)
57. Find \(\text{div} \, F\).
58. Find \(\text{curl} \, F\)
- Answer
- \(\text{curl }\, \vecs F = 2\vecs\omega\)
In the following exercises, suppose that \(\vecs \nabla \cdot \vecs F = 0\) and \(\vecs \nabla \cdot \vecs G = 0\).
59. Does \(\vecs F + \vecs G\) necessarily have zero divergence?
60. Does \(\vecs F \times \vecs G\) necessarily have zero divergence?
- Answer
- \(\vecs F \times \vecs G\) does not have zero divergence.
In the following exercises, suppose a solid object in \(\mathbb{R}^3\) has a temperature distribution given by \(T(x,y,z)\). The heat flow vector field in the object is \(\vecs F = - k \vecs \nabla T\), where \(k > 0\) is a property of the material. The heat flow vector points in the direction opposite to that of the gradient, which is the direction of greatest temperature decrease. The divergence of the heat flow vector is \(\vecs \nabla \cdot \vecs F = -k \vecs \nabla \cdot \vecs \nabla T = - k \vecs \nabla^2 T\).
61. Compute the heat flow vector field.
62. Compute the divergence.
- Answer
- \(\vecs \nabla \cdot \vecs F = -200 k [1 + 2(x^2 + y^2 + z^2)] e^{-x^2+y^2+z^2}\)
63. [T] Consider rotational velocity field \(\vecs v = \langle 0,10z, -10y \rangle\). If a paddlewheel is placed in plane \(x + y + z = 1\) with its axis normal to this plane, using a computer algebra system, calculate how fast the paddlewheel spins in revolutions per unit time.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.