4.2: Evaluating Algebraic Expressions

Last updated
Save as PDF

Page ID: 137917

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

In this section we will evaluate algebraic expressions for given values of the variables contained in the expressions. Here are some simple tips to help you be successful.

Tips for Evaluating Algebraic Expressions

Replace all occurrences of variables in the expression with open parentheses. Leave room between the parentheses to substitute the given value of the variable.
Substitute the given values of variables in the open parentheses prepared in the first step.
Evaluate the resulting expression according to the Rules Guiding Order of Operations.

Let's begin with an example.

Example 1

Evaluate the expression $x^2 − 2xy + y^2$ at $x = −3$ and $y = 2$.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression x² − 2xy + y² with open parentheses.

\[ x^2 -2xy + y^2 = ( ~ )^2 -2(~)(~) + ( ~ )^2 \nonumber\nonumber \]

Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.

\[ \begin{aligned} x^2 -2xy + y^2 ~ & \textcolor{red}{ \text{ Original expression.}} \\ =( \textcolor{red}{-3} )^2 -2 ( \textcolor{red}{-3})( \textcolor{red}{2}) + (\textcolor{red}{2})^2 ~ & \textcolor{red}{ \text{ Substitute } -3 \text{ for } x \text{and 2 for }y.} \\ =9-2(-3)(2)+4 ~ & \textcolor{red}{ \text{ Evaluate exponents first.}} \\ = 9-(-6)(2)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply } 2(-3)=-6.} \\ =9-(-12)+4 ~ & \textcolor{red}{ \text{ Left to right, multiply: } (-6)(2) = -12.} \\ = 9 + 12 + 4 ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = 25 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]

Exercise

If x = −2 and y = −1, evaluate x³ − y³.

Answer: −7

Example 2

Evaluate the expression (a − b)² for a = 3 and b = −5.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression (a − b)² with open parentheses.

\[ (a-b)^2 = (()-())^2\nonumber \]

Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.

\[ \begin{aligned} (a-b)^2 = (( \textcolor{red}{3})-( \textcolor{red}{-5}))^2 ~ & \textcolor{red}{ \text{ Substitute 3 for } a \text{ and } -5 \text{ for } b.} \\ = (3+5)^2 ~ & \textcolor{red}{ \text{ Add the opposite: } (3)-(-5)=3+5} \\ = 8^2 ~ & \textcolor{red}{ \text{ Simplify inside parentheses: } 3+5 = 8} \\ =64 ~ & \textcolor{red}{ \text{ Evaluate exponent: } 8^2 = 64} \end{aligned}\nonumber \]

Exercise

If a = 3 and b = −5, evaluate a² − b².

Answer: −16

Example 3

Evaluate the expression |a|−|b| at a = 5 and b = −7.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression |a|−|b| with open parentheses.

\[ |a| - |b| = |( ~ )| - |( ~ )|\nonumber \]

Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.

\[ \begin{aligned} |a| - |b| = |( \textcolor{red}{5} )| = |( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = 5 - 7 ~ & \textcolor{red}{ \text{ Absolute values first: } |(5)| = 5 \text{ and } |(-7)|=7|} \\ =5+(-7) ~ & \textcolor{red}{ \text{ Add the opposites: } 5 - 7 = 5+(-7).} \\ =-2 ~ & \textcolor{red}{ \text{ Add: } 5+(-7)=-2.} \end{aligned}\nonumber \]

Exercise

If a = 5 and b = −7, evaluate 2|a| − 3|b|.

Answer: −11

Example 4

Evaluate the expression |a − b| at a = 5 and b = −7.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression |a − b| with open parentheses.

\[ |a-b| = |(~)-(~)|\nonumber \]

Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.

\[ \begin{aligned} |a-b| = |( \textcolor{red}{5})-( \textcolor{red}{-7})| ~ & \textcolor{red}{ \text{ Substitute 5 for } a \text{ and } -7 \text{ for } b.} \\ = |5+7| ~ & \textcolor{red}{ \text{ Add the opposite: } 5-(-7)=5+7.} \\ =|12| ~ & \textcolor{red}{ \text{ Add: } 5+7=12.} \\ =12 ~ & \textcolor{red}{ \text{ Take the absolute value: } |12| = 12.} \end{aligned}\nonumber \]

Exercise

If a = 5 and b = −7, evaluate |2a − 3b|.

Answer: 31

Example 5

Evaluate the expression

\[ \frac{ad-bc}{a+b}\nonumber \]

at a = 5, b = −3, c = 2, and d = −4.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of variables in the expression with open parentheses.

\[ \frac{ad-bc}{a+b} = \frac{(~)(~)-(~)(~)}{(~)+(~)}\nonumber \]

Secondly, replace each variable with its given value, and thirdly, follow the “Rules Guiding Order of Operations” to evaluate the resulting expression.

\[ \begin{aligned} \frac{ad-bc}{a+b} = \frac{( \textcolor{red}{5}) -( \textcolor{red}{-3}) ( \textcolor{red}{2})}{( \textcolor{red}{5}) + ( \textcolor{red}{-3})} ~ & \textcolor{red}{ \text{ Substitute: } 5 \text{ for } a,~ -3 \text{ for } b,~ 2 \text{ for } c,~ -4 \text{ for } d.} \\ = \frac{-20-(-6)}{2} ~ & \begin{aligned} \textcolor{red}{ \text{ Numerator: } (5)(=4)=-20,~ (-3)(2) = -6.} \\ \textcolor{red}{ \text{ Denominator: } 5+(-3)=2.} \end{aligned} \\ = \frac{-20+6}{2} ~ & \textcolor{red}{ \text{ Numerator: Add the opposite.}} \\ = \frac{-14}{2} ~ & \textcolor{red}{ \text{ Numerator: } -20+6=-14.} \\ = -7 ~ & \textcolor{red}{ \text{Divide.}} \end{aligned}\nonumber \]

Exercise

If a = −7, b = −3, c = −15, and d = −14, evaluate:

\[\frac{a^2+b^2}{c+d}\nonumber \]

Answer: −2

Example 6

Pictured below is a rectangular prism.

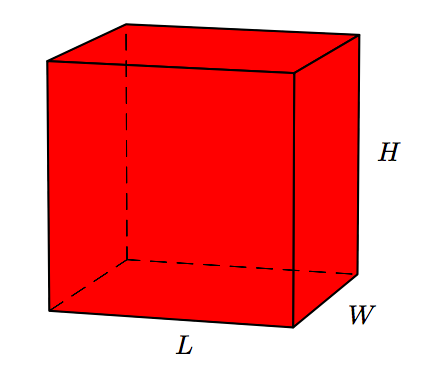
$Screen Shot 2019-08-19 at 6.09.16 PM.png$

The volume of the rectangular prism is given by the formula

\[V=LWH,\nonumber \]

where L is the length, W is the width, and H is the height of the rectangular prism. Find the volume of a rectangular prism having length 12 feet, width 4 feet, and height 6 feet.

Solution

Following “Tips for Evaluating Algebraic Expressions,” first replace all occurrences of of L, W, and H in the formula

\[ V = LWH\nonumber \]

with open parentheses.

\[V = (~)(~)(~)\nonumber \]

Next, substitute 12 ft for L, 4 ft for W, and 6 ft for H and simplify.

\[ \begin{aligned} V = (12 \text{ft})(4 \text{ft})(6 \text{ft}) \\ = 288 \text{ft}^3 \end{aligned}\nonumber \]

Hence, the volume of the rectangular prism is 288 cubic feet.

Exercise

The surface area of the prism pictured in this example is given by the following formula:

\[S = 2(W H + LH + LW) \nonumber \]

If L = 12, W = 4, and H = 6 feet, respectively, calculate the surface area.

Answer: 288 square feet

Exercises

Evaluate the expression at the given value of x and/or y.

1. −3x² − 6x + 3 at x = 7

3. −6x − 6 at x = 3

5. 5x² + 2x + 4 at x = −1

7. −9x − 5 at x = −2

11. 12x + 10 at x = −12

13. |x|−|y| at x = −5 and y = 4

15. −5x² + 2y² at x = 4 and y = 2

19. |x − y| at x = 4 and y = 5

21. 5x² − 4xy + 3y² at x = 1 and y = −4

23. |x − y| at x = 4 and y = 4

27. 5x² + 4y² at x = −2 and y = −2

33. $\frac{−4+9x}{7x}$ at x = 2

35. $\frac{−12 − 7x}{x}$ at x = −1

41. The formula

\[d=16t^2\nonumber \]

gives the distance (in feet) that an object falls from rest in terms of the time t that has elapsed since its release. Find the distance d (in feet) that an object falls in t = 4 seconds.

43. The formula

\[C = \frac{5(F − 32)}{9}\nonumber \]

gives the Celcius temperature C in terms of the Fahrenheit temperature F. Use the formula to find the Celsius temperature (◦ C) if the Fahrenheit temperature is F = 230◦ F.

Answers

1. −186

3. −24

5. 7

7. 13

11. −134

13. 1

15. −72

19. 1

21. 69

23. 0

27. 36

33. 1

35. 5

41. 256 feet

43. 110 degrees

Search

Text Color

Text Size

Margin Size

Font Type