6.2: Finding the Equation of a Line

The Slope-Intercept and Point-Slope Forms

In the previous sections we have been given an equation and have constructed the line to which it corresponds. Now, however, suppose we're given some geometric information about the line and we wish to construct the corresponding equation. We wish to find the equation of a line.

We know that the formula for the slope of a line is $m = \dfrac{y_2 - y_1}{x_2-x_1}$. We can find the equation of a line using the slope formula in either of two ways:

1

If we’re given the slope, $m$, and any point $(x_1, y_1)$ on the line, we can substitute this information into the formula for slope.
Let $(x_1, y_1)$ be the known point on the line and let $(x,y)$ be any other point on the line. Then

$\begin{aligned} m&=\dfrac{y-y_1}{x-x_1}&\text{ Multiply both sides by } x - x_1\\ m(x-x_1)&=(x-x_1) \cdot \dfrac{y-y_1}{x-x_1}\\ m(x-x_1)&=y-y_1&\text{ For convenience, we'll rewrite the equation. }\\ y-y_1&=m(x-x_1) \end{aligned}$

Since this equation was derived using a point and the slope of a line, it is called the point-slope form of a line.

2

If we are given the slope, $m$, $y$-intercept, $(0,b)$, we can substitute this information into the formula for slope.
Let $(0,b)$ be the $y$-intercept and (x,y) be any other point on the line. Then,

$\begin{aligned} m&=\dfrac{y-b}{x-0}\\ m&=\dfrac{y-b}{x}&\text{ Multiply both sides by } x\\ m \cdot x&=\not{x} \cdot \dfrac{y-b}{\not{x}}\\ mx&=y-b&\text{ Solve for } y\\ mx+b&=y&\text{ For convenience, we'll rewrite this equation}\\ y&=mx+b \end{aligned}$

Since this equation was derived using the slope and the intercept, it was called the slope-intercept form of a line.

We summarize these two derivations as follows.

Forms of the Equation of a Line

We can find the equation of a line if we’re given either of the following sets of information:

The slope, $m$, and the $y$-intercept, $(0, b)$, by substituting these values into:

$y = mx + b$

This is the slope-intercept form.

The slope, $m$, and any point $(x_1, y_1)$, by substituting these values into

$y-y_1 = m(x-x_1)$

This is the point-slope form.

Notice that both forms rely on knowing the slope. If we are given two points on the line we may still find the equation of the line passing through them by first finding the slope of the line, then using the point-slope form.

It is customary to use either the slope-intercept form or the general form for the final form of the line. We will use the slope-intercept form as the final form.

Sample Set A

Find the equation of the line using the given information.

Example $\PageIndex{1}$

$m = 6$, $y$-intercept $(0, 4)$

Since we're given the slope and the $y$-intercept, we'll use the slope-intercept form. $m = 6, b = 4$.

$y = mx + b$
$y = 6x + 4$

Example $\PageIndex{2}$

$m = -\dfrac{3}{4}$, $y$-intercept $(0, \dfrac{1}{8})$

Since we're given the slope and the $y$-intercept, we'll use the slope-intercept form. $m = \dfrac{-3}{4}$,

$b = \dfrac{1}{8}$
$y=mx + b$
$y = -\dfrac{3}{4}x + \dfrac{1}{8}$

Example $\PageIndex{3}$

$m = 2$, the point $(4, 3)$.

Since we're given the slope and some point, we'll use the point-slope form.

$y - y_1 = m(x - x_1)$. Let $(x_1, y_1)$ be $(4,3)$.
$y-3=2(x-4)$ Put this equation in slope-intercept form by solving for $y$.
$y-3=2x-8$
$y = 2x-5$

Example $\PageIndex{4}$

$m = -5$, the point $(-3, 0)$

Write the equation in slope-intercept form.

Since we're given the slope and some point, we'll use the point-slope form.

$\begin{aligned} y-y_1&=m(x-x_1)&\text{ Let } (x_1,y_1) \text{ be } (-3,0)\\ y-0&=-5[x-(-3)]\\ y&=-5(x+3)&\text{ Solve for } y\\ y&=-5x-15 \end{aligned}$

Example $\PageIndex{5}$

$m = -1$, the point $(0, 7)$.

Write the equation in slope-intercept form.

We're given the slope and a point, but careful observation reveals that this point is actually the $y$-intercept. Thus, we'll use the slope-intercept form. If we had not seen this point was the $y$-intercept we would have proceeded with the point-slope form. This would created slightly more work, but still give the same result.

Slope-Intercept Form:

$\begin{aligned} y&=mx + b\\ y&= -1x + 7\\ y&= -x + 7 \end{aligned}$

Point-Slope Form:

$\begin{aligned} y-y_1&=m(x-x_1)\\ y-7&=-1(x-0)\\ y-7&=-x\\ y&=-x+7 \end{aligned}$

Example $\PageIndex{6}$

The two points $(4, 1)$ and $(3, 5)$.

Write the equation in slope-intercept form.

Since we're given two points, we'll find the slope first.

$m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{5-1}{3-4} = \dfrac{4}{-1} = -4$

Now, we have the slope and two points, we can use either point and the point-slope form.

Using $(4, 1)$

$\begin{aligned} y-y_1&=m(x-x_1)\\ y-1&=-4(x-4)\\ y&=-4x+17 \end{aligned}$

Using $(3, 5)$

$\begin{aligned} y-y_1&=m(x-x_1)\\ y-5&=-4(x-3)\\ y-5&=-4x + 12\\ y&=-4x+17 \end{aligned}$

We can see that the use of either gives the same result.

Practice Set A

Find the equation of each line given the following information. Use the slope-intercept form as the final form of the equation.

Practice Problem $\PageIndex{1}$

$m=5$, $y$-intercept $(0,8)$.

Answer

$y=5x+8$

Practice Problem $\PageIndex{2}$

$m=-8$, $y$-intercept $(0,3)$.

Answer

$y=−8x+3$

Practice Problem $\PageIndex{3}$

$m=2$, $y$-intercept $(0,-7)$.

Answer

$y=2x−7$

Practice Problem $\PageIndex{4}$

$m=1$, $y$-intercept $(0,-1)$.

Answer

$y=x−1$

Practice Problem $\PageIndex{5}$

$m=-1$, $y$-intercept $(0,-10)$.

Answer

$y=−x−10$

Practice Problem $\PageIndex{6}$

$m=4$,the point $(5,2)$.

Answer

$y=4x−18$

Practice Problem $\PageIndex{7}$

$m=-6$,the point $(-1,0)$.

Answer

$y=−6x−6$

Practice Problem $\PageIndex{8}$

$m=-1$,the point $(-5,-5)$.

Answer

$y=−x−10$

Practice Problem $\PageIndex{9}$

The two points $(4, 1)$ and $(6, 5)$

Answer

$y=2x−7$

Practice Problem $\PageIndex{10}$

The two points $(−7,−1)$ and $(−4,8)$.

Answer

$y=3x+20$

Sample Set B

Example $\PageIndex{7}$

Find the equation of the line passing through the point $(4, -7)$ having slope $0$.

We're given the slope and some point, so we'll use the point-slope form. With $m = 0$ and $x_1, y_1)$ as $(4, -7)$, we have:

$\begin{aligned} y-y_1 &= m(x-x_1)\\ y-(-7)&=0(x-4)\\ y+7&=0\\ y&=-7 \end{aligned}$

This is a horizontal line

Example $\PageIndex{8}$

Find the equation of the line passing through the point $(1,3)$ given that the line is vertical.

Since the line is vertical, the slope does not exist. Thus, we cannot use either the slope-intercept form or the point-slope form. We must recall what we know about vertical lines. The equation of this line is simply $x=1$.

Practice Set B

Practice Problem $\PageIndex{11}$

Find the equation of the line passing throuhg the point $(2, 9)$ having slope $0$.

Answer

$y=9$

Practice Problem $\PageIndex{12}$

Find the equation of the line passing through the point $(−1,6)$ given that the line is vertical.

Answer

$x=−1$

Sample Set C

Example $\PageIndex{1}$

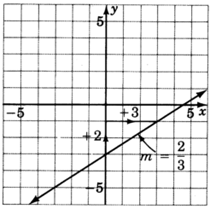
Reading only from the graph, determine the equation of the line.

The slope of the line is $\dfrac{2}{3}$, and the line crosses the $y$-axis at the point $(0, -3)$. Using the slope-intercept form we get:

$y = \dfrac{2}{3}x - 3$

Practice Set C

Practice Problem $\PageIndex{13}$

Reading only from the graph, determine the equation of the line.

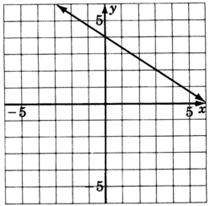
Answer

$y = \dfrac{-2}{3}x + 4$

Exercises

 

Suggested exercises for PrePALS: 6.2.39, 6.2.31, 6.2.35, 6.2.37, 6.2.39, 6.2.41, 6.2.42

 

For the following problems, write the equation of the line using the given information in slope-intercept form.

Exercise $\PageIndex{1}$

$m=3$, $y$-intercept $(0,4)$

Answer

$y=3x+4$

Exercise $\PageIndex{2}$

$m=2$, $y$-intercept $(0,5)$

Exercise $\PageIndex{3}$

$m=8$, $y$-intercept $(0,1)$

Answer

$y=8x+1$

Exercise $\PageIndex{4}$

$m=5$, $y$-intercept $(0,-3)$

Exercise $\PageIndex{5}$

$m=-6$, $y$-intercept $(0,-1)$

Answer

$y=−6x−1$

Exercise $\PageIndex{6}$

$m=-4$, $y$-intercept $(0,0)$

Exercise $\PageIndex{7}$

$m=-\dfrac{3}{2}$, $y$-intercept $(0,0)$

Answer

$y = -\dfrac{3}{2}x$

Exercise $\PageIndex{8}$

$m=3, (1,4)$

Exercise $\PageIndex{9}$

$m=1, (3,8)$

Answer

$y=x+5$

Exercise $\PageIndex{10}$

$m=2, (1,4)$

Exercise $\PageIndex{11}$

$m=8, (4,0)$

Answer

$y=8x−32$

Exercise $\PageIndex{12}$

$m=−3, (3,0)$

Exercise $\PageIndex{13}$

$m=−1, (6,0)$

Answer

$y=−x+6$

Exercise $\PageIndex{14}$

$m=−6, (0,0)$

Exercise $\PageIndex{15}$

$m=−2, (0,1)$

Answer

$y=−2x+1$

Exercise $\PageIndex{16}$

$(0,0), (3,2)$

Exercise $\PageIndex{17}$

$(0,0), (5,8)$

Answer

$y = \dfrac{8}{5}x$

Exercise $\PageIndex{18}$

$(4,1), (6,3)$

Exercise $\PageIndex{19}$

$(2,5), (1,4)$

Answer

$y=x+3$

Exercise $\PageIndex{20}$

$(5,−3), (6,2)$

Exercise $\PageIndex{21}$

$(2,3), (5,3)$

Answer

$y=3$ (horizontal line)

Exercise $\PageIndex{22}$

$(−1,5), (4,5)$

 

Exercise $\PageIndex{23}$

$(4,1), (4,2)$

Answer

$x=4$ (vertical line)

Exercise $\PageIndex{24}$

$(2,7), (2,8)$

Exercise $\PageIndex{25}$

$(3,3), (5,5)$

Answer

$y=x$

Exercise $\PageIndex{26}$

$(0,0), (1,1)$

Exercise $\PageIndex{27}$

$(−2,4), (3,−5)$

Answer

$y = -\dfrac{9}{5}x + \dfrac{2}{5}$

Exercise $\PageIndex{28}$

$(1,6), (−1,−6)$

Exercise $\PageIndex{29}$

$(14,12), (−9,−11)$

Answer

$y=x−2$

Exercise $\PageIndex{30}$

$(0,−4), (5,0)$

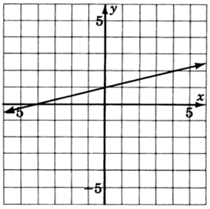
For the following problems, read only from the graph and determine the equation of the lines.

Exercise $\PageIndex{31}$

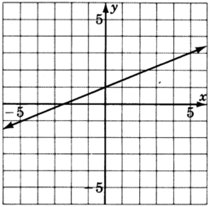
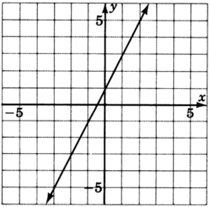
Answer

$y = \dfrac{2}{5}x + 1$

Exercise $\PageIndex{32}$

Exercise $\PageIndex{33}$

Answer

$y = \dfrac{1}{4}x + 1$

Exercise $\PageIndex{34}$

Exercise $\PageIndex{35}$

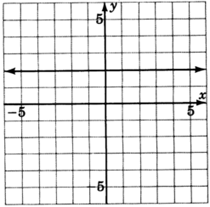
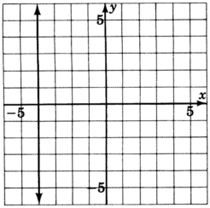
Answer

$x=−4$

Exercise $\PageIndex{36}$

Exercise $\PageIndex{37}$

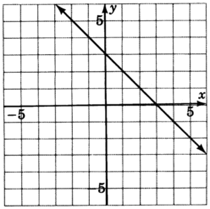
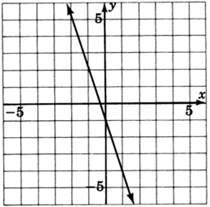
Answer

$y=−3x−1$

Exercises for Review

Exercise $\PageIndex{38}$

Graph the equation $x-3 = 0$

Exercise $\PageIndex{39}$

Supply the missing word. The point at which a line crosses the $y$-axis is called the ____

Answer

$y$-intercept

Exercise $\PageIndex{40}$

Supply the missing word. The ____ of a line is a measure of the steepness of the line.

Exercise $\PageIndex{41}$

Find the slope of the line that passes through the points $(4,0)$ and $(−2,−6)$.

Answer

$m=1$

Exercise $\PageIndex{42}$

Graph the equation $3y = 2x + 3$