13.E: Vector-Valued Functions (Exercises)
- Page ID
- 5777
13.1: Vector-Valued Functions and Space Curves
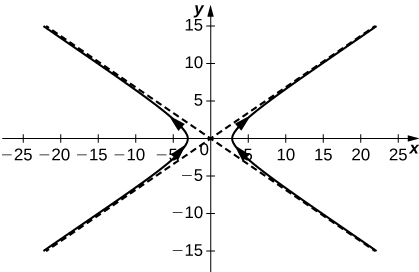
Give the component functions \(\mathrm{x=f(t)}\) and \(\mathrm{y=g(t)}\) for the vector-valued function \(\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}\).
\(\mathrm{f(t)=3 \sec t,g(t)=2 \tan t}\)
Given \(\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}\), find the following values (if possible).
- \(\mathrm{r(\frac{\pi}{4})}\)
- \(\mathrm{r(\pi)}\)
- \(\mathrm{r(\frac{\pi}{2})}\)
Sketch the curve of the vector-valued function \(\mathrm{r(t)=3 \sec t \mathbf{i}+2 \tan t \mathbf{j}}\) and give the orientation of the curve. Sketch asymptotes as a guide to the graph.
Evaluate \(\mathrm{\lim \limits_{t \to 0}⟨e^t \mathbf{i}+\frac{\sin t}{t} \mathbf{j}+e^{−t} \mathbf{k}⟩}\)
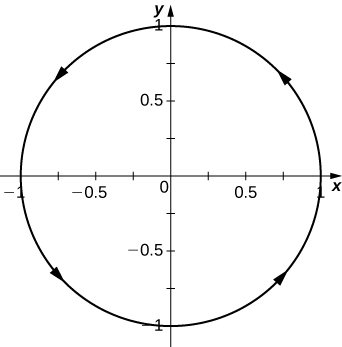
Given the vector-valued function \(\mathrm{r(t)=⟨\cos t,\sin t⟩}\) find the following values:
- \(\mathrm{\lim \limits_{t \to \frac{\pi}{4}} r(t)}\)
- \(\mathrm{r(\frac{\pi}{3})}\)
- Is \(\mathrm{r(t)}\) continuous at \(\mathrm{t=\frac{\pi}{3}}\)?
- Graph \(\mathrm{r(t)}\).
a. \(\mathrm{⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}}\)⟩, b. ⟨\(\mathrm{\frac{1}{2},\frac{\sqrt{3}}{2}}\)⟩, c. Yes, the limit as t approaches \(\mathrm{\frac{\pi}{3}}\) is equal to \(\mathrm{r(\frac{\pi}{3})}\), d.
Given the vector-valued function \(\mathrm{r(t)=⟨t,t^2+1⟩}\), find the following values:
- \(\mathrm{\lim \limits_{t \to -3} r(t)}\)
- (\mathrm{r(−3)}\)
- Is \(\mathrm{r(t)}\) continuous at \(\mathrm{x=−3}\)?
- \(\mathrm{r(t+2)−r(t)}\)
Let \(\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}\). Find the following values:
- \(\mathrm{r(\frac{\pi}{4})}\)
- \(\mathrm{\lim \limits_{t \to \frac{\pi}{4} } r(t)}\)
- Is \(\mathrm{r(t)}\) continuous at \(\mathrm{t=t=\frac{\pi}{4}}\)?
a. ⟨\(\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}\)⟩; b. ⟨\(\mathrm{e^{\frac{\pi}{4}},\frac{\sqrt{2}}{2},\ln (\frac{\pi}{4})}\)⟩; c. Yes
Find the limit of the following vector-valued functions at the indicated value of t.
\(\mathrm{\lim \limits_{t \to 4}⟨\sqrt{t−3},\frac{\sqrt{t}−2}{t−4},\tan(\frac{\pi}{t})⟩}\)
\(\mathrm{\lim \limits_{t \to \frac{\pi}{2}} r(t)}\) for \(\mathrm{r(t)=e^t \mathbf{i}+\sin t \mathbf{j}+\ln t \mathbf{k}}\)
\(\mathrm{⟨e^{\frac{\pi}{2}},1,\ln(\frac{\pi}{2})⟩}\)
\(\mathrm{\lim \limits_{t \to \infty}⟨e^{−2t},\frac{2t+3}{3t−1},\arctan(2t)⟩}\)
\(\mathrm{\lim \limits_{t \to \e^2}⟨t \ln (t),\frac{\ln t}{t^2},\sqrt{\ln(t^2)⟩}}\)
\(\mathrm{2e^2 \mathbf{i}+\frac{2}{e^4}\mathbf{j}+2\mathbf{k}}\)
\(\mathrm{\lim \limits_{t \to \frac{\pi}{6}}⟨\cos 2t,\sin 2t,1⟩}\)
\(\mathrm{\lim \limits_{t \to \infty} r(t)}\) for \(\mathrm{r(t)=2e^{−t} \mathbf{ i}+e^{−t} \mathbf{j}+\ln(t−1) \mathbf{k}}\)
The limit does not exist because the limit of \(\mathrm{\ln(t−1)}\) as t approaches infinity does not exist.
Describe the curve defined by the vector-valued function \(\mathrm{r(t)=(1+t)\mathbf{i}+(2+5t)\mathbf{j}+(−1+6t)\mathbf{k}}\).
Find the domain of the vector-valued functions.
Domain: \(\mathrm{r(t)=⟨t^2,\tan t,\ln t⟩}\)
\(\mathrm{t>0,t≠(2k+1)\frac{\pi}{2}}\), where k is an integer
Domain: \(\mathrm{r(t)=⟨t^2,\sqrt{t−3},\frac{3}{2t+1}⟩}\)
Domain: \(\mathrm{r(t)=⟨\csc(t),\frac{1}{\sqrt{t−3}}, \ln(t−2)⟩}\)
\(\mathrm{t>3,t≠n\pi}\), where n is an integer
Let \(\mathrm{r(t)=⟨\cos t,t,\sin t⟩}\) and use it to answer the following questions.
For what values of t is \(\mathrm{r(t)}\) continuous?
Sketch the graph of \(\mathrm{r(t)}\).
Find the domain of \(\mathrm{r(t)=2e^{-t} \mathbf{i}+e^{−t}\mathbf{j}+\ln(t−1)\mathbf{k}}\).
For what values of t is \(\mathrm{r(t)=2e_S^{-t} \mathbf{i}+e^{−t}\mathbf{j}+\ln(t−1)\mathbf{k}}\) continuous?
All t such that \(\mathrm{t∈(1,\infty)}\)
Eliminate the parameter t, write the equation in Cartesian coordinates, then sketch the graphs of the vector-valued functions. (Hint: Let \(\mathrm{x=2t}\) and \(\mathrm{y=t^2}\) Solve the first equation for x in terms of t and substitute this result into the second equation.)
\(\mathrm{r(t)=2t\mathbf{i}+t^2 \mathbf{j}}\)
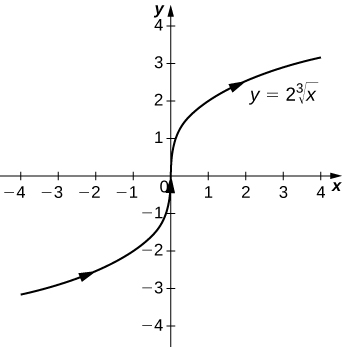
\(\mathrm{r(t)=t^3 \mathbf{i}+2t \mathbf{j}}\)
\(\mathrm{y=2\sqrt[3]{x}}\), a variation of the cube-root function
\(\mathrm{r(t)=2(\sinh t)\mathbf{i}+2(\cosh t) \mathbf{j},t>0}\)
\(\mathrm{r(t)=3(cost)i+3(sint)j}\)
\(\mathrm{x^2+y^2=9}\), a circle centered at \(\mathrm{(0,0)}\) with radius 3, and a counterclockwise orientation

\(\mathrm{r(t)=⟨3 \sin t,3 \cos t⟩}\)
Use a graphing utility to sketch each of the following vector-valued functions:
[T] \(\mathrm{r(t)=2 \cos t^2 \mathbf{i}+(2−\sqrt{t})\mathbf{j}}\)
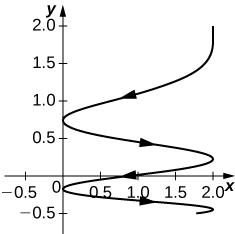
[T] \(\mathrm{r(t)=⟨e^{\cos (3t)},e^{−\sin(t)}⟩}\)
[T] \(\mathrm{r(t)=⟨2−\sin (2t),3+2 \cos t⟩}\)
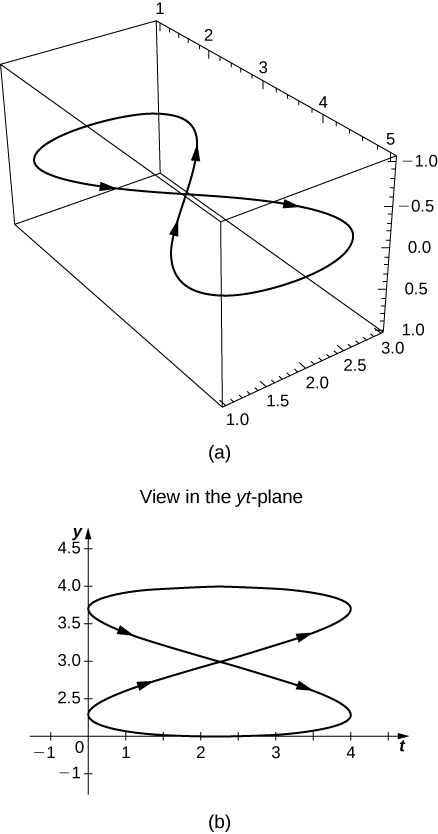 Find a vector-valued function that traces out the given curve in the indicated direction.
Find a vector-valued function that traces out the given curve in the indicated direction.
\(\mathrm{4x^2+9y^2=36}\); clockwise and counterclockwise
\(\mathrm{r(t)=⟨t,t^2⟩}\); from left to right
For left to right, \(\mathrm{y=x^2}\), where t increases
The line through P and Q where P is \(\mathrm{(1,4,−2)}\) and Q is \(\mathrm{(3,9,6)}\)
Consider the curve described by the vector-valued function \(\mathrm{r(t)=(50e^{−t}\cos t)\mathbf{i}+(50e^{−t}\sin t)\mathbf{j}+(5−5e^{−t})\mathbf{k}}\).
What is the initial point of the path corresponding to \(\mathrm{r(0)}\)?
\(\mathrm{(50,0,0)}\)
What is \(\mathrm{\lim \limits_{t \to \infty}r(t)} \)?
[T] Use technology to sketch the curve.
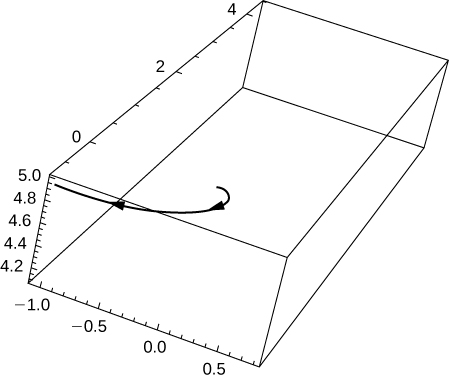
Eliminate the parameter t to show that \(\mathrm{z=5−\frac{r}{10}}\) where \(\mathrm{r=x^2+y^2}\).
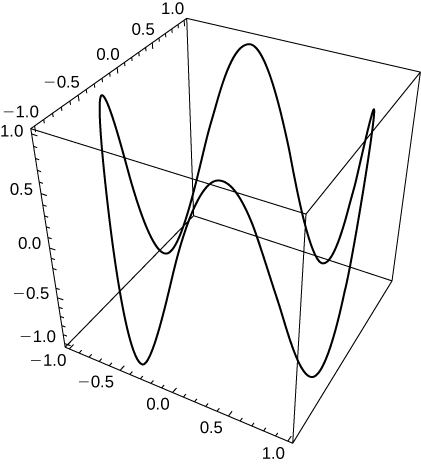
[T] Let \(\mathrm{r(t)=\cos t \mathbf{i}+\sin t\mathbf{j}+0.3 \sin (2t)\mathbf{k}}\). Use technology to graph the curve (called the roller-coaster curve) over the interval \(\mathrm{[0,2\pi)}\). Choose at least two views to determine the peaks and valleys.
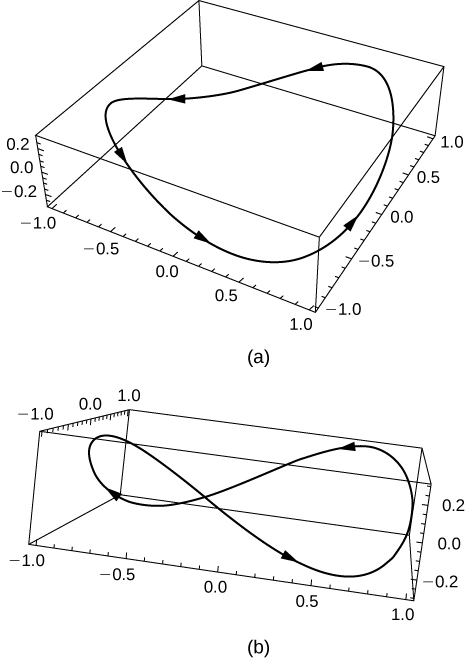
[T] Use the result of the preceding problem to construct an equation of a roller coaster with a steep drop from the peak and steep incline from the “valley.” Then, use technology to graph the equation.
Use the results of the preceding two problems to construct an equation of a path of a roller coaster with more than two turning points (peaks and valleys).
One possibility is \(\mathrm{r(t)=\cos t \mathbf{i}+\sin t\mathbf{j}+\sin (4t)\mathbf{k}}\). By increasing the coefficient of t in the third component, the number of turning points will increase.
- Graph the curve \(\mathrm{r(t)=(4+cos(18t))\cos(t)\mathbf{i}+(4+\cos (18t)sin(t))\mathbf{j}+0.3 \sin(18t)\mathbf{k}}\) using two viewing angles of your choice to see the overall shape of the curve.
- Does the curve resemble a “slinky”?
- What changes to the equation should be made to increase the number of coils of the slinky?
13.2: Calculus of Vector-Valued Functions
Compute the derivatives of the vector-valued functions.
\(\mathrm{r(t)=t^3 \mathbf{i}+3t^2 \mathbf{j}+\frac{t^3}{6}\mathbf{k}}\)
\(\mathrm{⟨3t^2,6t,\frac{1}{2}t^2⟩}\)
\(\mathrm{r(t)=\sin(t) \mathbf{i}+\cos(t) \mathbf{j}+e^t \mathbf{k}}\)
\(\mathrm{r(t)=e^{−t} \mathbf{i}+\sin(3t) \mathbf{j}+10 \sqrt{t} \mathbf{k}}\). A sketch of the graph is shown here. Notice the varying periodic nature of the graph.
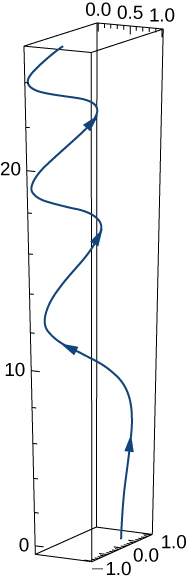
\(\mathrm{⟨−e^{−t},3\cos (3t),5t⟩}\)
\(\mathrm{r(t)=e^t \mathbf{i}+2e^t \mathbf{j}+\mathbf{k}}\)
\(\mathrm{r(t)=\mathbf{i}+\mathbf{j}+\mathbf{k}}\)
\(\mathrm{⟨0,0,0⟩}\)
\(\mathrm{r(t)=te^t \mathbf{i}+t \ln(t) \mathbf{j}+\sin(3t)\mathbf{k}}\)
\(\mathrm{r(t)=\frac{1}{t+1} \mathbf{i}+\arctan(t) \mathbf{j}+\ln t^3 \mathbf{k}}\)
\(\mathrm{⟨\frac{−1}{(t+1)^2},\frac{1}{1+t^2},\frac{3}{t}⟩}\)
\(\mathrm{r(t)= \tan(2t) \mathbf{i}+\sec(2t) \mathbf{j}+\sin ^2 (t) \mathbf{k}}\)
\(\mathrm{r(t)=3 \mathbf{i}+4 \sin (3t) \mathbf{j}+ t \cos(t) \mathbf{k}}\)
\(\mathrm{⟨0,12 \cos(3t), \cos t−t \sin t⟩}\)
\(\mathrm{r(t)=t^2 \mathbf{i}+te^{−2t} \mathbf{j}−5e^{−4t} \mathbf{k}}\)
For the following problems, find a tangent vector at the indicated value of t.
\(\mathrm{r(t)=t \mathbf{i}+\sin(2t) \mathbf{j}+\cos(3t) \mathbf{k}}\); \(\mathrm{t=\frac{π}{3}}\)
\(\mathrm{\frac{1}{\sqrt{2}}⟨1,−1,0⟩}\)
\(\mathrm{r(t)=3t^3 \mathbf{i}+2t^2 \mathbf{j}+\frac{1}{t} \mathbf{k};t=1}\)
\(\mathrm{r(t)=3e^t \mathbf{i}+2e^{−3t} \mathbf{j}+4e^{2t} \mathbf{k}; t= \ln(2)}\)
\(\mathrm{\frac{1}{\sqrt{1060.5625}}⟨6,−34,32⟩}\)
\(\mathrm{r(t)=\cos(2t) \mathbf{i}+2 \sin t \mathbf{j}+t^2 \mathbf{k};t=\frac{π}{2}}\)
Find the unit tangent vector for the following parameterized curves.
\(\mathrm{r(t)=6 \mathbf{i}+\cos(3t) \mathbf{j}+3\sin(4t) \mathbf{k}, 0≤t<2π}\)
\(\mathrm{\frac{1}{\sqrt{9sin ^2 (3t)+144\cos ^2 (4t)}}⟨0,−3\sin(3t),12\cos(4t)⟩}\)
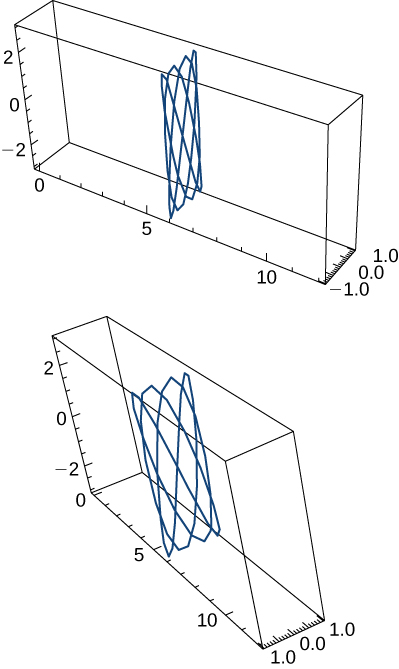
\(\mathrm{r(t)=\cos t \mathbf{i}+\sin t \mathbf{j}+\sin t \mathbf{k}, 0≤t<2π}\). Two views of this curve are presented here:
\(\mathrm{r(t)=3 \cos(4t) \mathbf{i}+3 \sin(4t) \mathbf{j}+5t \mathbf{k},1≤t≤2}\)
\(\mathrm{T(t)=−\frac{12}{13} \sin(4t) \mathbf{i}+ \frac{12}{13}\cos (4t) \mathbf{j}+\frac{5}{13} \mathbf{k}}\)
\(\mathrm{r(t)=t \mathbf{i}+3t \mathbf{j}+t^2 \mathbf{k}}\)
Let \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}−t^4 \mathbf{k}}\) and \(\mathrm{s(t)=\sin(t) \mathbf{i}+e^t \mathbf{j}+ \cos(t) \mathbf{k}}\) Here is the graph of the function:
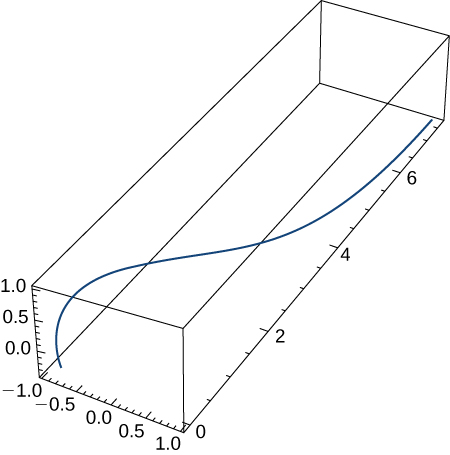
Find the following.
\(\mathrm{\frac{d}{dt}[r(t^2)]}\)
\(\mathrm{⟨2t,4t^3,−8t^7⟩}\)
\(\mathrm{\frac{d}{dt}[t^2⋅s(t)]}\)
\(\mathrm{\frac{d}{dt}[r(t)⋅s(t)]}\)
\(\mathrm{\sin(t)+2te^t−4t^3 \cos(t)+tcos(t)+t^2e^t+t^4sin(t)}\)
Compute the first, second, and third derivatives of \(\mathrm{r(t)=3t \mathbf{i}+6\ln(t) \mathbf{j}+5e^{−3t}\mathbf{k}}\).
Find \(\mathrm{r'(t)⋅r''(t) \; for \; r(t)=−3t^5 \mathbf{i}+5t \mathbf{j}+2t^2 \mathbf{k}.}\)
\(\mathrm{900t^7+16t}\)
The acceleration function, initial velocity, and initial position of a particle are
\(\mathrm{a(t)=−5 \cos t \mathbf{i}−5\sin t \mathbf{j},v(0)=9 \mathbf{i}+2 \mathbf{j},and \; r(0)=5 \mathbf{i}.}\) Find \(\mathrm{v(t) \; and \; r(t)}\).The position vector of a particle is \(\mathrm{r(t)=5 \sec(2t) \mathrm{i}−4tan(t) \mathrm{j}+7t^2 \mathrm{k}}\).
- Graph the position function and display a view of the graph that illustrates the asymptotic behavior of the function.
- Find the velocity as t approaches but is not equal to \(\mathrm{\frac{π}{4}}\) (if it exists).
-
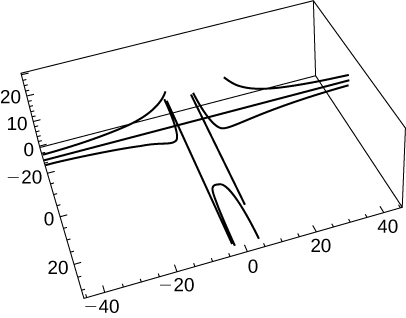
- Undefined or infinite
Find the velocity and the speed of a particle with the position function \(\mathrm{r(t)=(\frac{2t−1}{2t+1}) \mathbf{i}+\ln(1−4t^2) \mathbf{j}}\). The speed of a particle is the magnitude of the velocity and is represented by \(\mathrm{‖r′(t)‖}\).
A particle moves on a circular path of radius b according to the function \(\mathrm{r(t)=b \cos(\omega t) \mathbf{i}+b\sin(\omega) \mathbf{j},}\) where \(\mathrm{\omega}\) is the angular velocity, \(\mathrm{\frac{d \theta}{dt}}\).

Find the velocity function and show that \(\mathrm{v(t)}\) is always orthogonal to \(\mathrm{r(t)}\).
\(\mathrm{r'(t)=−b \omega \sin( \omega t) \mathbf{i}+b \omega cos(\omega t)\mathbf{j}}\). To show orthogonality, note that \(\mathrm{r'(t)⋅r(t)=0}\).
Show that the speed of the particle is proportional to the angular velocity.
Evaluate \(\mathrm{\frac{d}{dt}[u(t) \times u′(t)]}\) given \(\mathrm{u(t)=t^2 \mathbf{i}−2t \mathbf{j}+\mathbf{k}}\).
\(\mathrm{0 \mathbf{i} +2 \mathbf{j}+4t \mathbf{j}}\)
Find the antiderivative of \(\mathrm{r'(t)=\cos(2t) \mathbf{i}−2\sin t \mathbf{j}+\frac{1}{1+t^2} \mathbf{k}}\) that satisfies the initial condition \(\mathrm{r(0)=3 \mathbf{i}−2 \mathbf{j}+\mathbf{k}}\).
Evaluate \(\mathrm{\int_0^3‖ti+t^2j‖dt}\).
\(\mathrm{\frac{1}{3}(10^{\frac{3}{2}}−1)}\)
An object starts from rest at point \(\mathrm{P(1,2,0)}\) and moves with an acceleration of\(\mathrm{ a(t)=\mathbf{j}+2 \mathbf{k},}\) where \(\mathrm{‖a(t)‖}\) is measured in feet per second per second. Find the location of the object after \(\mathrm{t=2}\) sec.
Show that if the speed of a particle traveling along a curve represented by a vector-valued function is constant, then the velocity function is always perpendicular to the acceleration function.
\(\begin{align} \mathrm{‖v(t)‖ \;} & \mathrm{= k} \\ \mathrm{v(t)·v(t) \; } & \mathrm{= k} \\ \mathrm{ddt(v(t)·v(t)) \; } & \mathrm{=\frac{d}{dt}k=0} \\ \mathrm{v(t)·v′(t)+v′(t)·v(t) \;} & \mathrm{= 0} \\ \mathrm{2v(t)·v′(t) \;} & \mathrm{= 0} \\ \mathrm{v(t)·v′(t) \;} & \mathrm{= 0}\end{align}\)
The last statement implies that the velocity and acceleration are perpendicular or orthogonal.
Given \(\mathrm{r(t)=t \mathbf{i}+3t \mathbf{j}+t^2 \mathbf{k}}\) and \(\mathrm{u(t)=4t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k}}\), find \(\mathrm{\frac{d}{dt}(r(t) \times u(t))}\).
Given \(\mathrm{r(t)=⟨t+ \cos t,t− \sin t⟩}\), find the velocity and the speed at any time.
\(\mathrm{v(t)=⟨1− \sin t,1−\cos t⟩, speed=−v(t)‖=\sqrt{4−2( \sin t+\cos t)}}\)
Find the velocity vector for the function \(\mathrm{r(t)=⟨e^t,e^{−t},0⟩}\).
Find the equation of the tangent line to the curve \(\mathrm{r(t)=⟨e^t,e^{−t},0⟩}\) at \(\mathrm{t=0}\).
\(\mathrm{x−1=t,y−1=−t,z−0=0}\)
Describe and sketch the curve represented by the vector-valued function \(\mathrm{r(t)=⟨6t,6t−t^2⟩}\).
Locate the highest point on the curve \(\mathrm{r(t)=⟨6t,6t−t^2⟩}\) and give the value of the function at this point.
\(\mathrm{r(t)=⟨18,9⟩}\) at \(\mathrm{t=3}\)
The position vector for a particle is \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k}}\).The graph is shown here:
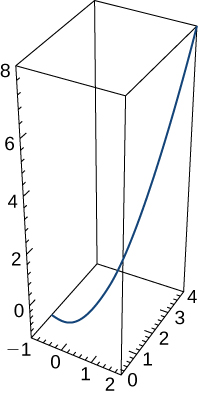
Find the velocity vector at any time.
Find the speed of the particle at time \(\mathrm{t=2}\) sec.
\(\mathrm{\sqrt{593}}\)
Find the acceleration at time \(\mathrm{t=2}\) sec.
A particle travels along the path of a helix with the equation \(\mathrm{r(t)= \cos(t) \mathbf{i}+\sin(t) \mathbf{j}+t \mathbf{k}}\). See the graph presented here:
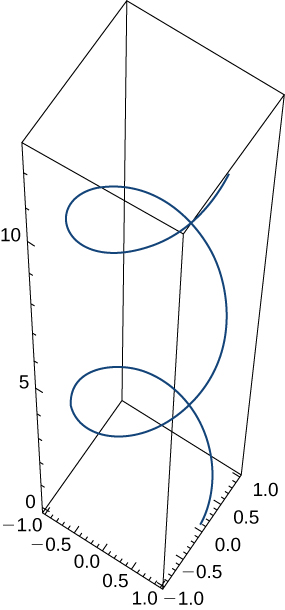
Find the following:
Velocity of the particle at any time
\(\mathrm{v(t)=⟨−\sin t,\cos t,1⟩}\)
Speed of the particle at any time
Acceleration of the particle at any time
\(\mathrm{a(t)=−\cos t \mathbf{i}− \sin t \mathbf{j}+0 \mathbf{j}}\)
Find the unit tangent vector for the helix.
A particle travels along the path of an ellipse with the equation \(\mathrm{r(t)=\cos t \mathbf{i}+2 \sin t \mathbf{j}+0 \mathbf{k}}\). Find the following:
Velocity of the particle
\(\mathrm{v(t)=⟨−\sin t,2 \cos t,0⟩}\)
Speed of the particle at \(\mathrm{t=\frac{π}{4}}\)
Acceleration of the particle at \(\mathrm{t=\frac{π}{4}}\)
\(\mathrm{a(t)=⟨−\frac{\sqrt{2}}{2},−\sqrt{2},0⟩}\)
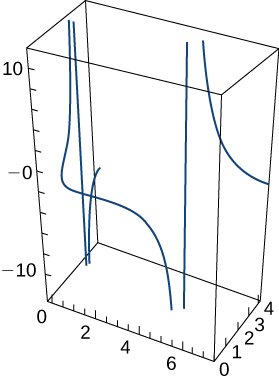
Given the vector-valued function \(\mathrm{r(t)=⟨\tan t,\sec t,0⟩}\) (graph is shown here), find the following:
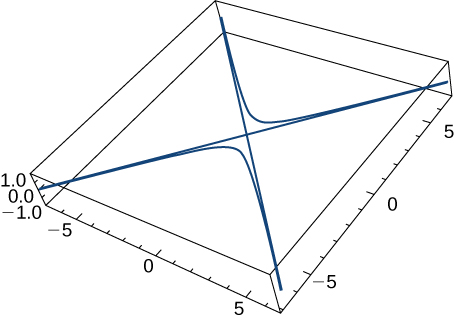
Velocity
Speed
\(\mathrm{‖v(t)‖=\sqrt{\sec ^4 t+\sec ^2 t \tan ^2 t}=\sqrt{\sec ^2 t(\sec ^2 t+\tan ^2 t)}}\)
Acceleration
Find the minimum speed of a particle traveling along the curve \(\mathrm{r(t)=⟨t+\cos t,t−\sin t⟩}\) \mathrm{t∈[0,2π)}\).
2
Given \(\mathrm{r(t)=t \mathbf{i}+2\sin t \mathbf{j}+2 \cos t \mathbf{k}}\) and \(\mathrm{u(t)=\frac{1}{t} \mathbf{i}+2 \sin t \mathbf{j}+2 \cos t \mathbf{k}}\), find the following:
\(\mathrm{r(t) \times u(t)}\)
\(\mathrm{\frac{d}{dt}(r(t) \times u(t))}\)
\(\mathrm{⟨0,2 \sin t(t− \frac{1}{t})−2 \cos t(1+ \frac{1}{t^2}),2 \sin t(1+ \frac{1}{t^2})+2 \cos t(t−\frac{2}{t})⟩}\)
Now, use the product rule for the derivative of the cross product of two vectors and show this result is the same as the answer for the preceding problem.
Find the unit tangent vector T(t) for the following vector-valued functions.
\(\mathrm{r(t)=⟨t,\frac{1}{t}⟩}\). The graph is shown here:
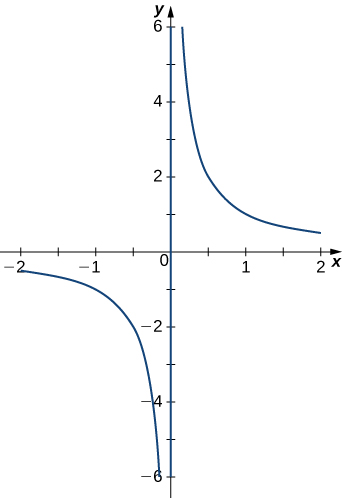
\(\mathrm{T(t)=⟨\frac{t^2}{\sqrt{t^4+1}},\frac{-1}{\sqrt{t^4+1}⟩}}\)
\(\mathrm{r(t)=⟨t \cos t,t sin t⟩}\)
\(\mathrm{r(t)=⟨t+1,2t+1,2t+2⟩}\)
\(\mathrm{T(t)=\frac{1}{3} ⟨1,2,2⟩}\)
Evaluate the following integrals:
\(\mathrm{\int (e^t \mathbf{i}+\sin t \mathbf{j}+ \frac{1}{2t−1} \mathbf{k})dt}\)
\(\mathrm{\int_0^1 r(t)dt}\), where \(\mathrm{r(t)=⟨\sqrt[3]{t},\frac{1}{t+1},e^{−t}⟩}\)
\(\mathrm{\frac{3}{4}\mathbf{i}+\ln(2) \mathbf{j}+(1−\frac{1}{e}) \mathbf{j}}\)
13.3: Arc Length and Curvature
Exercises
Find the arc length of the curve on the given interval.
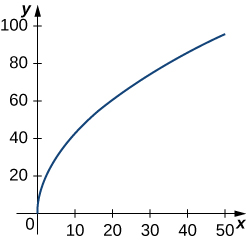
\(\mathrm{r(t)=t^2 \mathbf{i}+14t \mathbf{j},0≤t≤7}\). This portion of the graph is shown here:
\(\mathrm{r(t)=t^2 \mathbf{i}+(2t^2+1)\mathbf{j},1≤t≤3}\)
\(\mathrm{8\sqrt{5}}\)
\(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩,0≤t≤π}\). This portion of the graph is shown here:
\(\mathrm{r(t)=⟨t^2+1,4t^3+3⟩,−1≤t≤0}\)
\(\mathrm{\frac{1}{54}(37^{3/2}−1)}\)
\(\mathrm{r(t)=⟨e^{−t \cos t},e^{−t \sin t}⟩}\) over the interval \(\mathrm{[0,\frac{π}{2}]}\). Here is the portion of the graph on the indicated interval:
Find the length of one turn of the helix given by \(\mathrm{r(t)= \frac{1}{2} \cos t \mathbf{i}+\frac{1}{2} \sin t \mathbf{j}+\sqrt{\frac{3}{4}}t \mathbf{k}.}\)
Length \(\mathrm{=2π}\)
Find the arc length of the vector-valued function \(\mathrm{r(t)=−t \mathbf{i}+4t \mathbf{j}+3t \mathbf{k}}\) over \(\mathrm{[0,1]}\).
A particle travels in a circle with the equation of motion \(\mathrm{r(t)=3 \cos t \mathbf{i}+3 \sin t \mathbf{j} +0 \mathbf{k}}\). Find the distance traveled around the circle by the particle.
\(\mathrm{6π}\)
Set up an integral to find the circumference of the ellipse with the equation \(\mathrm{r(t)= \cos t \mathbf{i}+2 \sin t \mathbf{j}+0\mathbf{k}.}\)
Find the length of the curve \(\mathrm{r(t)=⟨\sqrt{2}t,e^t,e^{−t}⟩}\) over the interval \(\mathrm{0≤t≤1}\). The graph is shown here:
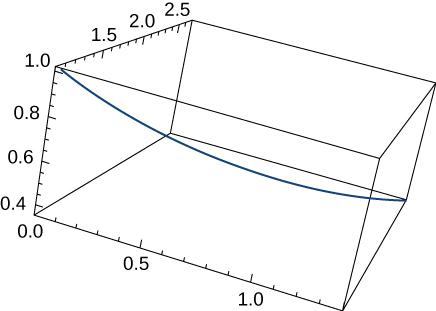
\(\mathrm{e−\frac{1}{e}}\)
Find the length of the curve \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\) for \(\mathrm{t∈[−10,10]}\).
The position function for a particle is \(\mathrm{r(t)=a \cos( ωt) \mathbf{i}+b \sin (ωt) \mathbf{j}}\). Find the unit tangent vector and the unit normal vector at \(\mathrm{t=0.}\)
\(\mathrm{T(0)= \mathbf{j}, N(0)=−\mathbf{i}}\)
Given \(\mathrm{r(t)=a \cos (ωt) \mathbf{i} +b \sin (ωt) \mathbf{j}}\), find the binormal vector \(\mathrm{B(0)}\).
Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), determine the tangent vector \(\mathrm{T(t)}\).
\(\mathrm{T(t)=⟨2e^t,e^t \cos t−e^t \sin t,e^t \cos t+e^t \sin t⟩}\)
Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), determine the unit tangent vector \(\mathrm{T(t)}\) evaluated at \(\mathrm{t=0}\).
Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), find the unit normal vector \(\mathrm{N(t)}\) evaluated at \(\mathrm{t=0}\), \(\mathrm{N(0)}\).
\(\mathrm{N(0)=⟨\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2}⟩}\)
Given \(\mathrm{r(t)=⟨2e^t,e^t \cos t,e^t \sin t⟩}\), find the unit normal vector evaluated at \(\mathrm{t=0}\).
Given \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}+t\mathbf{k}}\), find the unit tangent vector \(\mathrm{T(t)}\). The graph is shown here:
\(\mathrm{T(t)=\frac{1}{\sqrt{4t^2+2}}<1,2t,1>}\)
Find the unit tangent vector \(\mathrm{T(t)}\) and unit normal vector \(\mathrm{N(t)}\) at \(\mathrm{t=0}\) for the plane curve \(\mathrm{r(t)=⟨t^3−4t,5t^2−2⟩}\). The graph is shown here:
Find the unit tangent vector \(\mathrm{T(t)}\) for \(\mathrm{r(t)=3t \mathbf{i}+5t^2 \mathbf{j}+2t\mathbf{k}}\)
\(\mathrm{T(t)=\frac{1}{\sqrt{100t^2+13}}(3\mathbf{i}+10t\mathbf{j}+2\mathbf{k})}\)
Find the principal normal vector to the curve \(\mathrm{r(t)=⟨6 \cos t,6 \sin t⟩}\) at the point determined by \(\mathrm{t=π/3}\).
Find \(\mathrm{T(t)}\) for the curve \(\mathrm{r(t)=(t^3−4t) \mathbf{i}+(5t^2−2)\mathbf{j}}\).
\(\mathrm{T(t)=\frac{1}{\sqrt{9t^4+76t^2+16}}([3t^2−4]\mathbf{i}+10t\mathbf{j})}\)
Find \(\mathrm{N(t)}\) for the curve \(\mathrm{r(t)=(t^3−4t)\mathbf{i}+(5t^2−2)\mathbf{j}}\).
Find the unit normal vector \(\mathrm{N(t)}\) for \(\mathrm{r(t)=⟨2sint,5t,2cost⟩}\).
\(\mathrm{N(t)=⟨−sint,0,−cost⟩}\)
Find the unit tangent vector \(\mathrm{T(t)}\) for \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\).
Find the arc-length function \(\mathrm{s(t)}\) for the line segment given by \(\mathrm{r(t)=⟨3−3t,4t⟩}\). Write r as a parameter of s.
Arc-length function: \(\mathrm{s(t)=5t}\); r as a parameter of s: \(\mathrm{r(s)=(3−\frac{3s}{5})\mathbf{i}+\frac{4s}{5}\mathbf{j}}\)
Parameterize the helix \(\mathrm{r(t)= \cos t \mathbf{i}+ \sin t \mathbf{j}+t \mathbf{k}}\) using the arc-length parameter s, from \(\mathrm{t=0}\).
Parameterize the curve using the arc-length parameter s, at the point at which \(\mathrm{t=0}\) for \(\mathrm{r(t)=e^t \sin t \mathbf{i} + e^t \cos t \mathbf{j}}\)
\(\mathrm{(s)=(1+\frac{s}{\sqrt{2}}) \sin ( \ln (1+ \frac{s}{\sqrt{2}})) \mathbf{i} +(1+ \frac{s}{\sqrt{2}}) \cos [ \ln (1+\frac{s}{\sqrt{2}})]\mathbf{j}}\)
Find the curvature of the curve \(\mathrm{r(t)=5 \cos t \mathbf{i}+4 \sin t \mathbf{j}}\) at \(\mathrm{t=π/3}\). (Note: The graph is an ellipse.)
Find the x-coordinate at which the curvature of the curve \(\mathrm{y=1/x}\) is a maximum value.
The maximum value of the curvature occurs at \(\mathrm{x=\sqrt[4]{5}}\).
Find the curvature of the curve \(\mathrm{r(t)=5 \cos t \mathbf{i}+5 \sin t \mathbf{j}}\). Does the curvature depend upon the parameter t?
Find the curvature \(κ\) for the curve \(\mathrm{y=x−\frac{1}{4}x^2}\) at the point \(\mathrm{x=2}\).
\(\mathrm{\frac{1}{2}}\)
Find the curvature \(κ\) for the curve \(\mathrm{y=\frac{1}{3}x^3}\) at the point \(\mathrm{x=1}\).
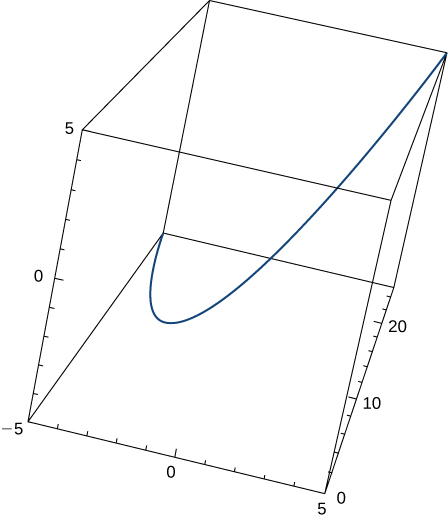
Find the curvature κκ of the curve \(\mathrm{r(t)=t \mathbf{i}+6t^2 \mathbf{j}+4t \mathbf{k}}\). The graph is shown here:
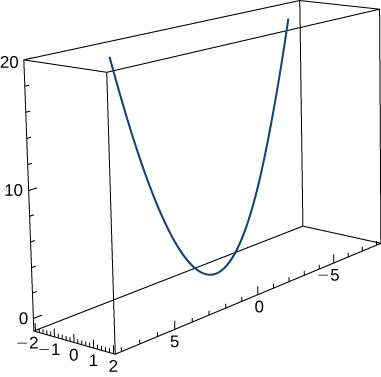
\(\mathrm{κ≈\frac{49.477}{(17+144t^2)^{3/2}}}\)
Find the curvature of \(\mathrm{r(t)=⟨2 \sin t,5t,2 \cos t⟩}\).
Find the curvature of \(\mathrm{r(t)=\sqrt{2}t \mathbf{i}+e^t \mathbf{j}+e^{−t} \mathbf{k}}\) at point \(\mathrm{P(0,1,1)}\).
\(\mathrm{\frac{1}{2\sqrt{2}}}\)
At what point does the curve \(\mathrm{y=e^x}\) have maximum curvature?
What happens to the curvature as \(\mathrm{x→∞}\) for the curve \(\mathrm{y=e^x}\)?
The curvature approaches zero.
Find the point of maximum curvature on the curve \(\mathrm{y=\ln x}\).
Find the equations of the normal plane and the osculating plane of the curve \(\mathrm{r(t)=⟨2 \sin (3t),t,2 \cos (3t)⟩}\) at point \(\mathrm{(0,π,−2)}\).
\(\mathrm{y=6x+π}\) and \(\mathrm{x+6=6π}\)
Find equations of the osculating circles of the ellipse \(\mathrm{4y^2+9x^2=36}\) at the points \(\mathrm{(2,0)}\) and \(\mathrm{(0,3)}\).
Find the equation for the osculating plane at point \(\mathrm{t=π/4}\) on the curve \(\mathrm{r(t)=\cos (2t) \mathbf{i}+ \sin (2t) \mathbf{j}+t}\).
\(\mathrm{x+2z=\frac{π}{2}}\)
Find the radius of curvature of \(\mathrm{6y=x^3}\) at the point \(\mathrm{(2,\frac{4}{3}).}\)
Find the curvature at each point \(\mathrm{(x,y)}\) on the hyperbola \(\mathrm{r(t)=⟨a \cosh( t),b \sinh (t)⟩}\).
\(\mathrm{\frac{a^4b^4}{(b^4x^2+a^4y^2)^{3/2}}}\)
Calculate the curvature of the circular helix \(\mathrm{r(t)=r \sin (t) \mathbf{i}+r \cos (t) \mathbf{j}+t \mathbf{k}}\).
Find the radius of curvature of \(\mathrm{y= \ln (x+1)}\) at point \(\mathrm{(2,\ln 3)}\).
\(\mathrm{\frac{10\sqrt{10}}{3}}\)
Find the radius of curvature of the hyperbola \(\mathrm{xy=1}\) at point \(\mathrm{(1,1)}\).
A particle moves along the plane curve C described by \(\mathrm{r(t)=t \mathbf{i}+t^2 \mathbf{j}}\). Solve the following problems.
Find the length of the curve over the interval \(\mathrm{[0,2]}\).
\(\mathrm{\frac{38}{3}}\)
Find the curvature of the plane curve at \(\mathrm{t=0,1,2}\).
Describe the curvature as t increases from \(\mathrm{t=0}\) to \(\mathrm{t=2}\).
The curvature is decreasing over this interval.
The surface of a large cup is formed by revolving the graph of the function \(\mathrm{y=0.25x^{1.6}}\) from \(\mathrm{x=0}\) to \(\mathrm{x=5}\) about the y-axis (measured in centimeters).
[T] Use technology to graph the surface.
Find the curvature \(κ\) of the generating curve as a function of x.
\(\mathrm{κ=\frac{6}{x^{2/5}(25+4x^{6/5})}}\)
[T] Use technology to graph the curvature function.
13.4: Motion in Space
aN=a⋅N=‖v×a‖‖v‖=‖a‖2−aT−−−−−−−−−√aN=a·N=‖v×a‖‖v‖=‖a‖2−aT2
Given r(t)=(3t2−2)i+(2t−sin(t))j,r(t)=(3t2−2)i+(2t−sin(t))j, find the velocity of a particle moving along this curve.
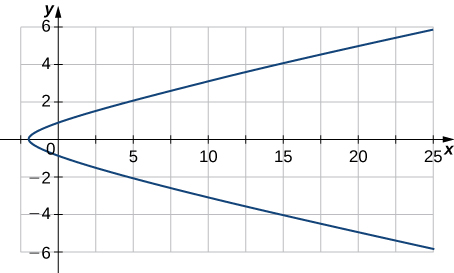
v(t)=(6t)i+(2−cos(t))jv(t)=(6t)i+(2−cos(t))j
Given r(t)=(3t2−2)i+(2t−sin(t))j,r(t)=(3t2−2)i+(2t−sin(t))j, find the acceleration vector of a particle moving along the curve in the preceding exercise.
Given the following position functions, find the velocity, acceleration, and speed in terms of the parameter t.
r(t)=⟨3cost,3sint,t2⟩r(t)=⟨3cost,3sint,t2⟩
v(t)=⟨−3sint,3cost,2t⟩,v(t)=⟨−3sint,3cost,2t⟩, a(t)=⟨−3cost,−3sint,2⟩,a(t)=⟨−3cost,−3sint,2⟩, speed=9+4t2−−−−−−√speed=9+4t2
r(t)=e−ti+t2j+tantkr(t)=e−ti+t2j+tantk
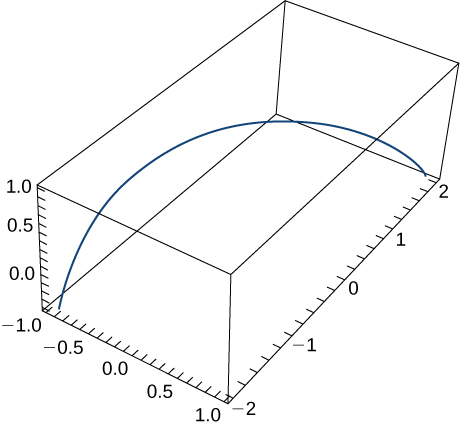
r(t)=2costj+3sintk.r(t)=2costj+3sintk. The graph is shown here:
v(t)=−2sintj+3costk,v(t)=−2sintj+3costk, a(t)=−2costj−3sintk,a(t)=−2costj−3sintk, speed=4sin2(t)+9cos2(t)−−−−−−−−−−−−−−√speed=4sin2(t)+9cos2(t)
Find the velocity, acceleration, and speed of a particle with the given position function.
r(t)=⟨t2−1,t⟩r(t)=⟨t2−1,t⟩
r(t)=⟨et,e−t⟩r(t)=⟨et,e−t⟩
v(t)=eti−e−tj,v(t)=eti−e−tj, a(t)=eti+e−tj,a(t)=eti+e−tj, ∥v(t)∥e2t+e−2t−−−−−−−−√‖v(t)‖e2t+e−2t
r(t)=⟨sint,t,cost⟩.r(t)=⟨sint,t,cost⟩. The graph is shown here:
The position function of an object is given by r(t)=⟨t2,5t,t2−16t⟩.r(t)=⟨t2,5t,t2−16t⟩. At what time is the speed a minimum?
t=4t=4
Let r(t)=rcosh(ωt)i+rsinh(ωt)j.r(t)=rcosh(ωt)i+rsinh(ωt)j. Find the velocity and acceleration vectors and show that the acceleration is proportional to r(t).r(t).
Consider the motion of a point on the circumference of a rolling circle. As the circle rolls, it generates the cycloid r(t)=(ωt−sin(ωt))i+(1−cos(ωt))j,r(t)=(ωt−sin(ωt))i+(1−cos(ωt))j, where ωω is the angular velocity of the circle and b is the radius of the circle:
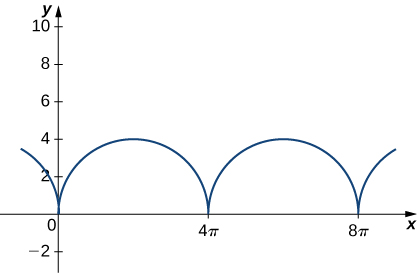
Find the equations for the velocity, acceleration, and speed of the particle at any time.
v(t)=(ω−ωcos(ωt))i+(ωsin(ωt))j,v(t)=(ω−ωcos(ωt))i+(ωsin(ωt))j,
a(t)=(ω2sin(ωt))i+(ω2cos(ωt))j,a(t)=(ω2sin(ωt))i+(ω2cos(ωt))j,
speed=ω2−2ω2cos(ωt)+ω2cos2(ωt)+ω2sin2(ωt)−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√=2ω2(1−cos(ωt))−−−−−−−−−−−−−√speed=ω2−2ω2cos(ωt)+ω2cos2(ωt)+ω2sin2(ωt)=2ω2(1−cos(ωt))
A person on a hang glider is spiraling upward as a result of the rapidly rising air on a path having position vector r(t)=(3cost)i+(3sint)j+t2k.r(t)=(3cost)i+(3sint)j+t2k. The path is similar to that of a helix, although it is not a helix. The graph is shown here:
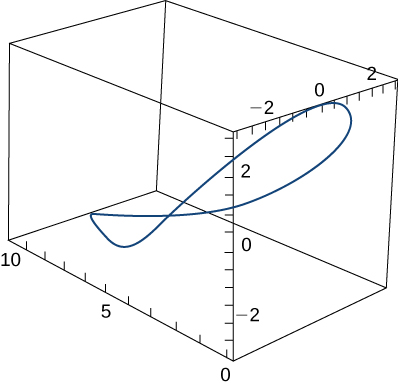
Find the following quantities:
The velocity and acceleration vectors
The glider’s speed at any time
∥v(t)∥=9+4t2−−−−−−√‖v(t)‖=9+4t2
The times, if any, at which the glider’s acceleration is orthogonal to its velocity
Given that r(t)=⟨e−5tsint,e−5tcost,4e−5t⟩r(t)=⟨e−5tsint,e−5tcost,4e−5t⟩ is the position vector of a moving particle, find the following quantities:
The velocity of the particle
v(t)=⟨e−5t(cost−5sint),−e−5t(sint+5cost),−20e−5t⟩v(t)=⟨e−5t(cost−5sint),−e−5t(sint+5cost),−20e−5t⟩
The speed of the particle
The acceleration of the particle
a(t)=⟨e−5t(−sint−5cost)−5e−5t(cost−5sint),a(t)=⟨e−5t(−sint−5cost)−5e−5t(cost−5sint), −e−5t(cost−5sint)+5e−5t(sint+5cost),100e−5t⟩−e−5t(cost−5sint)+5e−5t(sint+5cost),100e−5t⟩
Find the maximum speed of a point on the circumference of an automobile tire of radius 1 ft when the automobile is traveling at 55 mph.
A projectile is shot in the air from ground level with an initial velocity of 500 m/sec at an angle of 60° with the horizontal. The graph is shown here:
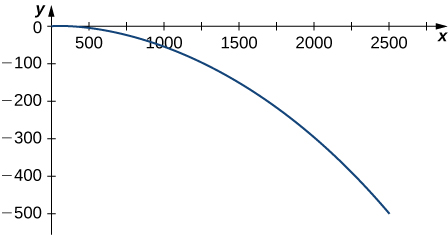
At what time does the projectile reach maximum height?
44.185 sec
What is the approximate maximum height of the projectile?
At what time is the maximum range of the projectile attained?
t=88.37t=88.37 sec
What is the maximum range?
What is the total flight time of the projectile?
88.37 sec
A projectile is fired at a height of 1.5 m above the ground with an initial velocity of 100 m/sec and at an angle of 30° above the horizontal. Use this information to answer the following questions:
Determine the maximum height of the projectile.
Determine the range of the projectile.
The range is approximately 886.29 m.
A golf ball is hit in a horizontal direction off the top edge of a building that is 100 ft tall. How fast must the ball be launched to land 450 ft away?
A projectile is fired from ground level at an angle of 8° with the horizontal. The projectile is to have a range of 50 m. Find the minimum velocity necessary to achieve this range.
v=42.16v=42.16 m/sec
Prove that an object moving in a straight line at a constant speed has an acceleration of zero.
The acceleration of an object is given by a(t)=tj+tk.a(t)=tj+tk. The velocity at t=1t=1 sec is v(1)=5jv(1)=5j and the position of the object at t=1t=1sec is r(1)=0i+0j+0k.r(1)=0i+0j+0k. Find the object’s position at any time.
r(t)=0i+(16t3+4.5t−143)j+(t36−12t+13)kr(t)=0i+(16t3+4.5t−143)j+(t36−12t+13)k
Find r(t)r(t) given that a(t)=−32j,a(t)=−32j, v(0)=6003√i+600j,v(0)=6003i+600j, and r(0)=0.r(0)=0.
Find the tangential and normal components of acceleration for r(t)=acos(ωt)i+bsin(ωt)jr(t)=acos(ωt)i+bsin(ωt)j at t=0.t=0.
aT=0,aT=0, aN=aω2aN=aω2
Given r(t)=t2i+2tjr(t)=t2i+2tj and t=1,t=1, find the tangential and normal components of acceleration.
For each of the following problems, find the tangential and normal components of acceleration.
r(t)=⟨etcost,etsint,et⟩.r(t)=⟨etcost,etsint,et⟩. The graph is shown here:
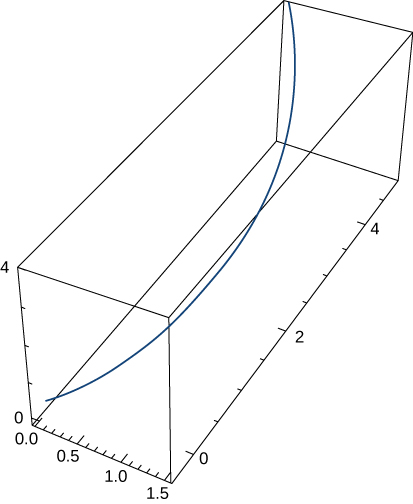
aT=3√et,aT=3et, aN=2√etaN=2et
r(t)=⟨cos(2t),sin(2t),1⟩r(t)=⟨cos(2t),sin(2t),1⟩
r(t)=⟨2t,t2,t33⟩r(t)=⟨2t,t2,t33⟩
aT=2t,aT=2t, aN=4+2t2aN=4+2t2
r(t)=⟨23(1+t)3/2,23(1−t)3/2,2√t⟩r(t)=⟨23(1+t)3/2,23(1−t)3/2,2t⟩
r(t)=⟨6t,3t2,2t3⟩r(t)=⟨6t,3t2,2t3⟩
aT6t+12t31+t4+t2√,aT6t+12t31+t4+t2, aN=61+4t2+t41+t2+t4−−−−−−√aN=61+4t2+t41+t2+t4
r(t)=t2i+t2j+t3kr(t)=t2i+t2j+t3k
r(t)=3cos(2πt)i+3sin(2πt)jr(t)=3cos(2πt)i+3sin(2πt)j
aT=0,aT=0, aN=23√πaN=23π
Find the position vector-valued function r(t),r(t), given that a(t)=i+etj,a(t)=i+etj, v(0)=2j,v(0)=2j, and r(0)=2i.r(0)=2i.
The force on a particle is given by f(t)=(cost)i+(sint)j.f(t)=(cost)i+(sint)j. The particle is located at point (c,0)(c,0) at t=0.t=0. The initial velocity of the particle is given by v(0)=v0j.v(0)=v0j. Find the path of the particle of mass m. (Recall, F=m⋅a.)F=m·a.)
r(t)=(−1mcost+c+1m)i+(−sintm+(v0+1m)t)jr(t)=(−1mcost+c+1m)i+(−sintm+(v0+1m)t)j
An automobile that weighs 2700 lb makes a turn on a flat road while traveling at 56 ft/sec. If the radius of the turn is 70 ft, what is the required frictional force to keep the car from skidding?
Using Kepler’s laws, it can be shown that v0=2GMr0−−−−√v0=2GMr0 is the minimum speed needed when θ=0θ=0 so that an object will escape from the pull of a central force resulting from mass M. Use this result to find the minimum speed when θ=0θ=0 for a space capsule to escape from the gravitational pull of Earth if the probe is at an altitude of 300 km above Earth’s surface.
10.94 km/sec
Find the time in years it takes the dwarf planet Pluto to make one orbit about the Sun given that a=39.5a=39.5 A.U.
Suppose that the position function for an object in three dimensions is given by the equation r(t)=tcos(t)i+tsin(t)j+3tk.r(t)=tcos(t)i+tsin(t)j+3tk.
Show that the particle moves on a circular cone.
Find the angle between the velocity and acceleration vectors when t=1.5.t=1.5.
Find the tangential and normal components of acceleration when t=1.5.t=1.5.
aT=0.43m/sec2,aT=0.43m/sec2,
aN=2.46m/sec2aN=2.46m/sec2
Chapter Review Exercises
True or False? Justify your answer with a proof or a counterexample.
A parametric equation that passes through points P and Q can be given by r(t)=⟨t2,3t+1,t−2⟩,r(t)=⟨t2,3t+1,t−2⟩, where P(1,4,−1)P(1,4,−1) and Q(16,11,2).Q(16,11,2).
ddt[u(t)×u(t)]=2u′(t)×u(t)ddt[u(t)×u(t)]=2u′(t)×u(t)
False, ddt[u(t)×u(t)]=0ddt[u(t)×u(t)]=0
The curvature of a circle of radius rr is constant everywhere. Furthermore, the curvature is equal to 1/r.1/r.
The speed of a particle with a position function r(t)r(t) is (r′(t))/(|r′(t)|).(r′(t))/(|r′(t)|).
False, it is |r′(t)||r′(t)|
Find the domains of the vector-valued functions.
r(t)=⟨sin(t),ln(t),t√⟩r(t)=⟨sin(t),ln(t),t⟩
r(t)=⟨et,14−t√,sec(t)⟩r(t)=⟨et,14−t,sec(t)⟩
t<4,t<4, t≠nπ2t≠nπ2
Sketch the curves for the following vector equations. Use a calculator if needed.
[T] r(t)=⟨t2,t3⟩r(t)=⟨t2,t3⟩
[T] r(t)=⟨sin(20t)e−t,cos(20t)e−t,e−t⟩r(t)=⟨sin(20t)e−t,cos(20t)e−t,e−t⟩
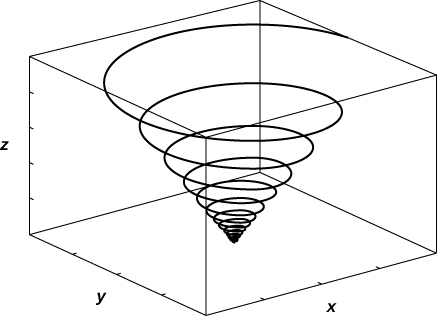
Find a vector function that describes the following curves.
Intersection of the cylinder x2+y2=4x2+y2=4 with the plane x+z=6x+z=6
Intersection of the cone z=x2+y2−−−−−−√z=x2+y2 and plane z=y−4z=y−4
r(t)=⟨t,2−t28,−2−t28⟩r(t)=⟨t,2−t28,−2−t28⟩
Find the derivatives of u(t),u(t), u′(t),u′(t), u′(t)×u(t),u′(t)×u(t), u(t)×u′(t),u(t)×u′(t), and u(t)⋅u′(t).u(t)·u′(t). Find the unit tangent vector.
u(t)=⟨et,e−t⟩u(t)=⟨et,e−t⟩
u(t)=⟨t2,2t+6,4t5−12⟩u(t)=⟨t2,2t+6,4t5−12⟩
u′(t)=⟨2t,2,20t4⟩,u′(t)=⟨2t,2,20t4⟩, u′′(t)=⟨2,0,80t3⟩,u″(t)=⟨2,0,80t3⟩, ddt[u′(t)×u(t)]=⟨−480t3−160t4,24+75t2,12+4t⟩,ddt[u′(t)×u(t)]=⟨−480t3−160t4,24+75t2,12+4t⟩, ddt[u(t)×u′(t)]=⟨480t3+160t4,−24−75t2,−12−4t⟩,ddt[u(t)×u′(t)]=⟨480t3+160t4,−24−75t2,−12−4t⟩, ddt[u(t)⋅u′(t)]=720t8−9600t3+6t2+4,ddt[u(t)·u′(t)]=720t8−9600t3+6t2+4, unit tangent vector: T(t)=2t400t8+4t2+4√i+2400t8+4t2+4√j+20t4400t8+4t2+4√kT(t)=2t400t8+4t2+4i+2400t8+4t2+4j+20t4400t8+4t2+4k
Evaluate the following integrals.
∫(tan(t)sec(t)i−te3tj)dt∫(tan(t)sec(t)i−te3tj)dt
∫14u(t)dt,∫14u(t)dt, with u(t)=⟨ln(t)t,1t√,sin(tπ4)⟩u(t)=⟨ln(t)t,1t,sin(tπ4)⟩
ln(4)22i+2j+2(2+2√)πkln(4)22i+2j+2(2+2)πk
Find the length for the following curves.
r(t)=⟨3(t),4cos(t),4sin(t)⟩r(t)=⟨3(t),4cos(t),4sin(t)⟩ for 1≤t≤41≤t≤4
r(t)=2i+tj+3t2kr(t)=2i+tj+3t2k for 0≤t≤10≤t≤1
37√2+112sinh−1(6)372+112sinh−1(6)
Reparameterize the following functions with respect to their arc length measured from t=0t=0 in direction of increasing t.t.
r(t)=2ti+(4t−5)j+(1−3t)kr(t)=2ti+(4t−5)j+(1−3t)k
r(t)=cos(2t)i+8tj−sin(2t)kr(t)=cos(2t)i+8tj−sin(2t)k
r(t(s))=cos(2s65√)i+8s65√j−sin(2s65√)kr(t(s))=cos(2s65)i+8s65j−sin(2s65)k
Find the curvature for the following vector functions.
r(t)=(2sint)i−4tj+(2cost)kr(t)=(2sint)i−4tj+(2cost)k
r(t)=2√eti+2√e−tj+2tkr(t)=2eti+2e−tj+2tk
e2t(e2t+1)2e2t(e2t+1)2
Find the unit tangent vector, the unit normal vector, and the binormal vector for r(t)=2costi+3tj+2sintk.r(t)=2costi+3tj+2sintk.
Find the tangential and normal acceleration components with the position vector r(t)=⟨cost,sint,et⟩.r(t)=⟨cost,sint,et⟩.
aT=e2t1+e2t√,aT=e2t1+e2t, aN=2e2t+4e2tsintcost+1√1+e2t√aN=2e2t+4e2tsintcost+11+e2t
A Ferris wheel car is moving at a constant speed vv and has a constant radius r.r. Find the tangential and normal acceleration of the Ferris wheel car.
The position of a particle is given by r(t)=⟨t2,ln(t),sin(πt)⟩,r(t)=⟨t2,ln(t),sin(πt)⟩, where tt is measured in seconds and rr is measured in meters. Find the velocity, acceleration, and speed functions. What are the position, velocity, speed, and acceleration of the particle at 1 sec?
v(t)=⟨2t,1t,cos(πt)⟩v(t)=⟨2t,1t,cos(πt)⟩ m/sec, a(t)=⟨2,−1t2,−sin(πt)⟩m/sec2,a(t)=⟨2,−1t2,−sin(πt)⟩m/sec2, speed=4t2+1t2+cos2(πt)−−−−−−−−−−−−−−−√speed=4t2+1t2+cos2(πt) m/sec; at t=1,t=1, r(1)=⟨1,0,0⟩r(1)=⟨1,0,0⟩ m, v(1)=⟨2,−1,1⟩v(1)=⟨2,−1,1⟩ m/sec, a(1)=⟨2,−1,0⟩a(1)=⟨2,−1,0⟩ m/sec2, and speed=6√speed=6 m/sec
The following problems consider launching a cannonball out of a cannon. The cannonball is shot out of the cannon with an angle θθ and initial velocity v0.v0. The only force acting on the cannonball is gravity, so we begin with a constant acceleration a(t)=−gj.a(t)=−gj.
Find the velocity vector function v(t).v(t).
Find the position vector r(t)r(t) and the parametric representation for the position.
r(t)=v0t−g2t2j,r(t)=v0t−g2t2j, r(t)=⟨v0(cosθ)t,v0(sinθ)t,−g2t2⟩r(t)=⟨v0(cosθ)t,v0(sinθ)t,−g2t2⟩
At what angle do you need to fire the cannonball for the horizontal distance to be greatest? What is the total distance it would travel?


