12.E: Vectors in Space (Exercises)

12.1: Vectors in the Plane

For the following exercises, consider points \(P(−1,3), Q(1,5),\) and \(R(−3,7)\). Determine the requested vectors and express each of them a. in component form and b. by using the standard unit vectors.

1) \(\vec{PQ}\)

Solution: \(a. \vec{PQ}=⟨2,2⟩; b. \vec{PQ}=2i+2j\)

2) \(\vec{PR}\)

3) \(\vec{QP}\)

Solution: \(a. \vec{QP}=⟨−2,−2⟩; b. \vec{QP}=−2i−2j\)

4) \(\vec{RP}\)

5) \(\vec{PQ}+\vec{PR}\)

Solution: \(a. \vec{PQ}+\vec{PR}=⟨0,6⟩; b. \vec{PQ}+\vec{PR}=6j\)

6) \(\vec{PQ}−\vec{PR}\)

7) \(2\vec{PQ}−2\vec{PR}\)

Solution: \(a. 2\vec{PQ}→−2\vec{PR}=⟨8,−4⟩; b. 2\vec{PQ}−2\vec{PR}=8i−4j\)

8) \(2\vec{PQ}+\frac{1}{2}\vec{PR}\)

9) The unit vector in the direction of \(\vec{PQ}\)

Solution: \(a. ⟨\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}⟩; b. \frac{1}{\sqrt{2}}i+\frac{1}{\sqrt{2}}j\)

10) The unit vector in the direction of \(\vec{PR}\)

11) A vector \(v\) has initial point \((−1,−3)\) and terminal point \((2,1)\). Find the unit vector in the direction of \(v\). Express the answer in component form.

Solution: \(⟨\frac{3}{5},\frac{4}{5}⟩\)

12) A vector \(v\) has initial point \((−2,5)\) and terminal point \((3,−1)\). Find the unit vector in the direction of \(v\). Express the answer in component form.

13) The vector \(v\) has initial point \(P(1,0)\) and terminal point \(Q\) that is on the y-axis and above the initial point. Find the coordinates of terminal point \(Q\) such that the magnitude of the vector \(v\) is \(\sqrt{5}\).

Solution: \(Q(0,2)\)

14) The vector \(v\) has initial point \(P(1,1)\) and terminal point \(Q\) that is on the x-axis and left of the initial point. Find the coordinates of terminal point \(Q\) such that the magnitude of the vector \(v\) is \(\sqrt{10}\).

For the following exercises, use the given vectors \(a\) and \(b\).

a. Determine the vector sum \(a+b\) and express it in both the component form and by using the standard unit vectors.

b. Find the vector difference \(a−b\) and express it in both the component form and by using the standard unit vectors.

c. Verify that the vectors \(a, b,\) and \(a+b\), and, respectively, \(a, b\), and \(a−b\) satisfy the triangle inequality.

d. Determine the vectors \(2a, −b,\) and \(2a−b.\) Express the vectors in both the component form and by using standard unit vectors.

15) \(a=2i+j, b=i+3j\)

Solution: \(a. a+b=3i+4j, a+b=⟨3,4⟩;\) b. \(a−b=i−2j, a−b=⟨1,−2⟩;\) c. Answers will vary; d. \(2a=4i+2j, 2a=⟨4,2⟩, −b=−i−3j, −b=⟨−1,−3⟩, 2a−b=3i−j, 2a−b=⟨3,−1⟩\)

16) \(a=2i, b=−2i+2j\)

17) Let \(a\) be a standard-position vector with terminal point \((−2,−4)\). Let \(b\) be a vector with initial point \((1,2)\) and terminal point \((−1,4)\). Find the magnitude of vector \(−3a+b−4i+j.\)

Solution: \(15\)

18) Let \(a\) be a standard-position vector with terminal point at \((2,5)\). Let \(b\) be a vector with initial point \((−1,3)\) and terminal point \((1,0)\). Find the magnitude of vector \(a−3b+14i−14j.\)

19) Let \(u\) and \(v\) be two nonzero vectors that are nonequivalent. Consider the vectors \(a=4u+5v\) and \(b=u+2v\) defined in terms of \(u\) and \(v\). Find the scalar \(λ\) such that vectors \(a+λb\) and \(u−v\) are equivalent.

Solution: \(λ=−3\)

20) Let \(u\) and \(v\) be two nonzero vectors that are nonequivalent. Consider the vectors \(a=2u−4v\) and \(b=3u−7v\) defined in terms of \(u\) and \(v\). Find the scalars \(α\) and \(β\) such that vectors \(αa+βb\) and \(u−v\) are equivalent.

21) Consider the vector \(a(t)=⟨cost,sint⟩\) with components that depend on a real number \(t\). As the number \(t\) varies, the components of \(a(t)\) change as well, depending on the functions that define them.

a. Write the vectors \(a(0)\) and \(a(π)\) in component form.

b. Show that the magnitude \(∥a(t)∥\) of vector \(a(t)\) remains constant for any real number \(t\).

c. As \(t\) varies, show that the terminal point of vector \(a(t)\) describes a circle centered at the origin of radius \(1\).

Solution: \(a. a(0)=⟨1,0⟩, a(π)=⟨−1,0⟩;\) b. Answers may vary; c. Answers may vary

22) Consider vector \(a(x)=⟨x,\sqrt{1−x^2}⟩\) with components that depend on a real number \(x∈[−1,1]\). As the number \(x\) varies, the components of \(a(x)\) change as well, depending on the functions that define them.

a. Write the vectors \(a(0)\) and \(a(1)\) in component form.

b. Show that the magnitude \(∥a(x)∥\) of vector \(a(x)\) remains constant for any real number \(x\)

c. As \(x\) varies, show that the terminal point of vector \(a(x)\) describes a circle centered at the origin of radius \(1\).

23) Show that vectors \(a(t)=⟨cost,sint⟩\) and \(a(x)=⟨x,\sqrt{1−x^2}⟩\) are equivalent for \(x=r\) and \(t=2kπ\), where \(k\) is an integer.

Solution: Answers may vary

24) Show that vectors \(a(t)=⟨cost,sint⟩\) and \(a(x)=⟨x,\sqrt{1−x^2}⟩\) are opposite for \(x=r\) and \(t=π+2kπ\), where \(k\) is an integer.

For the following exercises, find vector \(v\) with the given magnitude and in the same direction as vector \(u\).

25) \(‖v‖=7,u=⟨3,4⟩\)

Solution: \(v=⟨\frac{21}{5},\frac{28}{5}⟩\)

26) \(‖v‖=3,u=⟨−2,5⟩\)

27) \(‖v‖=7,u=⟨3,−5⟩\)

Solution: \(v=⟨\frac{21\sqrt{34}}{34},−\frac{35\sqrt{34}}{34}⟩\)

28) \(‖v‖=10,u=⟨2,−1⟩\)

For the following exercises, find the component form of vector \(u\), given its magnitude and the angle the vector makes with the positive x-axis. Give exact answers when possible.

29) \(‖u‖=2, θ=30°\)

Solution: \(u=⟨\sqrt{3},1⟩\)

30) \(‖u‖=6, θ=60°\)

31) \(‖u‖=5, θ=\frac{π}{2}\)

Solution: \(u=⟨0,5⟩\)

32) \(‖u‖=8, θ=π\)

33) \(‖u‖=10, θ=\frac{5π}{6}\)

Solution: \(u=⟨−5\sqrt{3},5⟩\)

34) \(‖u‖=50, θ=\frac{3π}{4}\)

For the following exercises, vector \(u\) is given. Find the angle \(θ∈[0,2π)\) that vector \(u\) makes with the positive direction of the x-axis, in a counter-clockwise direction.

35) \(u=5\sqrt{2}i−5\sqrt{2}j\)

Solution: \(θ=\frac{7π}{4}\)

36) \(u=−\sqrt{3}i−j\)

37) Let \(a=⟨a_1,a_2⟩, b=⟨b_1,b_2⟩\), and \(c=⟨c_1,c_2⟩\) be three nonzero vectors. If \(a_1b_2−a_2b_1≠0\), then show there are two scalars, \(α\) and \(β\), such that \(c=αa+βb.\)

Solution: Answers may vary

38) Consider vectors \(a=⟨2,−4⟩, b=⟨−1,2⟩,\) and \(0\) Determine the scalars \(α\) and \(β\) such that \(c=αa+βb\).

39) Let \(P(x_0,f(x_0))\) be a fixed point on the graph of the differential function \(f\) with a domain that is the set of real numbers.

a. Determine the real number \(z_0\) such that point \(Q(x_0+1,z_0)\) is situated on the line tangent to the graph of \(f\) at point \(P\).

b. Determine the unit vector \(u\) with initial point \(P\) and terminal point \(Q\).

Solution: \(a. z_0=f(x_0)+f′(x_0); b. u=\frac{1}{\sqrt{1+[f′(x_0)]^2}}⟨1,f′(x_0)⟩\)

40) Consider the function \(f(x)=x^4,\) where \(x∈R\).

a. Determine the real number \(z_0\) such that point \(Q(2,z_0)\) s situated on the line tangent to the graph of \(f\) at point \(P(1,1)\).

b. Determine the unit vector \(u\) with initial point \(P\) and terminal point \(Q\).

41) Consider \(f\) and \(g\) two functions defined on the same set of real numbers \(D\). Let \(a=⟨x,f(x)⟩\) and \(b=⟨x,g(x)⟩\) be two vectors that describe the graphs of the functions, where \(x∈D\). Show that if the graphs of the functions \(f\) and \(g\) do not intersect, then the vectors \(a\) and \(b\) are not equivalent.

42) Find \(x∈R\) such that vectors \(a=⟨x,sinx⟩\) and \(b=⟨x,cosx⟩\) are equivalent.

43) Calculate the coordinates of point \(D\) such that \(ABCD\) is a parallelogram, with \(A(1,1), B(2,4)\), and \(C(7,4)\).

Solution: \(D(6,1)\)

44) Consider the points \(A(2,1), B(10,6), C(13,4), and D(16,−2).\) Determine the component form of vector \(\vec{AD}\).

45) The speed of an object is the magnitude of its related velocity vector. A football thrown by a quarterback has an initial speed of \(70\) mph and an angle of elevation of \(30°\). Determine the velocity vector in mph and express it in component form. (Round to two decimal places.)

Solution: \(⟨60.62,35⟩\)

46) A baseball player throws a baseball at an angle of \(30°\) with the horizontal. If the initial speed of the ball is \(100\) mph, find the horizontal and vertical components of the initial velocity vector of the baseball. (Round to two decimal places.)

47) A bullet is fired with an initial velocity of \(1500\) ft/sec at an angle of \(60°\) with the horizontal. Find the horizontal and vertical components of the velocity vector of the bullet. (Round to two decimal places.)

Solution: The horizontal and vertical components are \(750\) ft/sec and \(1299.04\) ft/sec, respectively.

48) [T] A 65-kg sprinter exerts a force of \(798\) N at a \(19°\) angle with respect to the ground on the starting block at the instant a race begins. Find the horizontal component of the force. (Round to two decimal places.)

49) [T] Two forces, a horizontal force of \(45\) lb and another of \(52\) lb, act on the same object. The angle between these forces is \(25°\). Find the magnitude and direction angle from the positive x-axis of the resultant force that acts on the object. (Round to two decimal places.)

Solution: The magnitude of resultant force is \(94.71\) lb; the direction angle is \(13.42°\).

50) [T] Two forces, a vertical force of \(26\) lb and another of \(45\) lb, act on the same object. The angle between these forces is \(55°\). Find the magnitude and direction angle from the positive x-axis of the resultant force that acts on the object. (Round to two decimal places.)

51) [T] Three forces act on object. Two of the forces have the magnitudes \(58\) N and \(27\) N, and make angles \(53°\) and \(152°\), respectively, with the positive x-axis. Find the magnitude and the direction angle from the positive x-axis of the third force such that the resultant force acting on the object is zero. (Round to two decimal places.)

Solution: The magnitude of the third vector is \(60.03\)N; the direction angle is \(259.38°\).

52) Three forces with magnitudes 80 lb, 120 lb, and 60 lb act on an object at angles of \(45°, 60°\) and \(30°\), respectively, with the positive x-axis. Find the magnitude and direction angle from the positive x-axis of the resultant force. (Round to two decimal places.)

53) [T] An airplane is flying in the direction of \(43°\) east of north (also abbreviated as \(N43E\)) at a speed of \(550\) mph. A wind with speed \(25\) mph comes from the southwest at a bearing of \(N15E\). What are the ground speed and new direction of the airplane?

Solution: The new ground speed of the airplane is \(572.19\) mph; the new direction is \(N41.82E.\)

54) [T] A boat is traveling in the water at \(30\) mph in a direction of \(N20E\) (that is, \(20°\) east of north). A strong current is moving at \(15\) mph in a direction of \(N45E\). What are the new speed and direction of the boat?

55) [T] A 50-lb weight is hung by a cable so that the two portions of the cable make angles of \(40°\) and \(53°\), respectively, with the horizontal. Find the magnitudes of the forces of tension \(T_1\) and \(T_2\) in the cables if the resultant force acting on the object is zero. (Round to two decimal places.)

Solution: \(∥T_1∥=30.13lb, ∥T_2∥=38.35lb\)

56) [T] A 62-lb weight hangs from a rope that makes the angles of \(29°\) and \(61°\), respectively, with the horizontal. Find the magnitudes of the forces of tension \(T_1\) and \(T_2\) in the cables if the resultant force acting on the object is zero. (Round to two decimal places.)

57) [T] A 1500-lb boat is parked on a ramp that makes an angle of \(30°\) with the horizontal. The boat’s weight vector points downward and is a sum of two vectors: a horizontal vector \(v_1\) that is parallel to the ramp and a vertical vector \(v_2\) that is perpendicular to the inclined surface. The magnitudes of vectors \(v_1\) and \(v_2\) are the horizontal and vertical component, respectively, of the boat’s weight vector. Find the magnitudes of \(v_1\) and \(v_2\). (Round to the nearest integer.)

Solution: \(∥v1∥=750 lb, ∥v2∥=1299 lb\)

58) [T] An 85-lb box is at rest on a \(26°\) incline. Determine the magnitude of the force parallel to the incline necessary to keep the box from sliding. (Round to the nearest integer.)

59) A guy-wire supports a pole that is \(75\) ft high. One end of the wire is attached to the top of the pole and the other end is anchored to the ground \(50\) ft from the base of the pole. Determine the horizontal and vertical components of the force of tension in the wire if its magnitude is \(50\) lb. (Round to the nearest integer.)

Solution: The two horizontal and vertical components of the force of tension are \(28\) lb and \(42\) lb, respectively.

60) A telephone pole guy-wire has an angle of elevation of \(35°\) with respect to the ground. The force of tension in the guy-wire is \(120\) lb. Find the horizontal and vertical components of the force of tension. (Round to the nearest integer.)

12.2: Vectors in Three Dimensions

Consider a rectangular box with one of the vertices at the origin, as shown in the following figure. If point \(\displaystyle A(2,3,5)\) is the opposite vertex to the origin, then find

a. the coordinates of the other six vertices of the box and

b. the length of the diagonal of the box determined by the vertices \(\displaystyle O\) and \(\displaystyle A\).

Solution: \(\displaystyle a. (2,0,5),(2,0,0),(2,3,0),(0,3,0),(0,3,5),(0,0,5); b. \sqrt{38}\)

2) Find the coordinates of point \(\displaystyle P\) and determine its distance to the origin.

For the following exercises, describe and graph the set of points that satisfies the given equation.

3) \(\displaystyle (y−5)(z−6)=0\)

Solution: A union of two planes: \(\displaystyle y=5\) (a plane parallel to the xz-plane) and \(\displaystyle z=6\) (a plane parallel to the xy-plane)

4) \(\displaystyle (z−2)(z−5)=0\)

5) \(\displaystyle (y−1)^2+(z−1)^2=1\)

Solution: A cylinder of radius \(\displaystyle 1\) centered on the line \(\displaystyle y=1,z=1\)

6) \(\displaystyle (x−2)^2+(z−5)^2=4\)

7) Write the equation of the plane passing through point \(\displaystyle (1,1,1)\) that is parallel to the xy-plane.

Solution: \(\displaystyle z=1\)

8) Write the equation of the plane passing through point \(\displaystyle (1,−3,2)\) that is parallel to the xz-plane.

9) Find an equation of the plane passing through points \(\displaystyle 1,−3,−2), (0,3,−2),\) and \(\displaystyle (1,0,−2).\)

Solution: \(\displaystyle z=−2\)

10) Find an equation of the plane passing through points \(\displaystyle (1,9,2), (1,3,6),\) and \(\displaystyle (1,−7,8).\)

For the following exercises, find the equation of the sphere in standard form that satisfies the given conditions.

11) Center \(\displaystyle C(−1,7,4)\) and radius \(\displaystyle 4\)

Solution: \(\displaystyle (x+1)^2+(y−7)^2+(z−4)^2=16\)

12) Center \(\displaystyle C(−4,7,2)\) and radius \(\displaystyle 6\)

13) Diameter \(\displaystyle PQ,\) where \(\displaystyle P(−1,5,7)\) and \(\displaystyle Q(−5,2,9)\)

Solution: \(\displaystyle (x+3)^2+(y−3.5)^2+(z−8)^2=\frac{29}{4}\)

14) Diameter \(\displaystyle PQ,\) where \(\displaystyle P(−16,−3,9)\) and \(\displaystyle Q(−2,3,5)\)

For the following exercises, find the center and radius of the sphere with an equation in general form that is given.

15) \(\displaystyle P(1,2,3) x^2+y^2+z^2−4z+3=0\)

Solution: Center \(\displaystyle C(0,0,2)\) and radius \(\displaystyle 1\)

16) \(\displaystyle x^2+y^2+z^2−6x+8y−10z+25=0\)

For the following exercises, express vector \(\displaystyle \vec{PQ}\) with the initial point at \(\displaystyle P\) and the terminal point at \(\displaystyle Q\)

a. in component form and

b. by using standard unit vectors.

17) \(\displaystyle P(3,0,2)\) and \(\displaystyle Q(−1,−1,4)\)

Solution: \(\displaystyle a. \vec{PQ}=⟨−4,−1,2⟩; b. \vec{PQ}=−4i−j+2k\)

18) \(\displaystyle P(0,10,5)\) and \(\displaystyle Q(1,1,−3)\)

19) \(\displaystyle P(−2,5,−8)\) and \(\displaystyle M(1,−7,4)\), where \(\displaystyle M\) is the midpoint of the line segment \(\displaystyle PQ\)

Solution: \(\displaystyle a. \vec{PQ}=⟨6,−24,24⟩; . \vec{PQ}=6i−24j+24k\)

20) \(\displaystyle Q(0,7,−6)\) and \(\displaystyle M(−1,3,2)\), where \(\displaystyle M\) is the midpoint of the line segment \(\displaystyle PQ\)

21) Find terminal point \(\displaystyle Q\) of vector \(\displaystyle \vec{PQ}=⟨7,−1,3⟩\) with the initial point at \(\displaystyle P(−2,3,5).\)

Solution: \(\displaystyle Q(5,2,8)\)

22) Find initial point \(\displaystyle P\) of vector \(\displaystyle \vec{PQ}=⟨−9,1,2⟩\) with the terminal point at \(\displaystyle Q(10,0,−1).\)

For the following exercises, use the given vectors \(\displaystyle a\) and \(\displaystyle b\) to find and express the vectors \(\displaystyle a+b, 4a\), and \(\displaystyle −5a+3b\) in component form.

23) \(\displaystyle a=⟨−1,−2,4⟩, b=⟨−5,6,−7⟩\)

Solution: \(\displaystyle a+b=⟨−6,4,−3⟩, 4a=⟨−4,−8,16⟩, −5a+3b=⟨−10,28,−41⟩\)

24) \(\displaystyle a=⟨3,−2,4⟩, b=⟨−5,6,−9⟩\)

25) \(\displaystyle a=−k, b=−i\)

Solution: \(\displaystyle a+b=⟨−1,0,−1⟩, 4a=⟨0,0,−4⟩, −5a+3b=⟨−3,0,5⟩\)

26) \(\displaystyle a=i+j+k, b=2i−3j+2k\)

For the following exercises, vectors \(\displaystyle u\) and \(\displaystyle v\) are given. Find the magnitudes of vectors \(\displaystyle u−v\) and \(\displaystyle −2u\).

27) \(\displaystyle u=2i+3j+4k, v=−i+5j−k\)

Solution: \(\displaystyle ‖u−v‖=\sqrt{38}, ‖−2u‖=2\sqrt{29}\)

28) \(\displaystyle u=i+j, v=j−k\)

29) \(\displaystyle u=⟨2cost,−2sint,3⟩, v=⟨0,0,3⟩,\) where \(\displaystyle t\) is a real number.

Solution: \(\displaystyle ‖u−v‖=2, ‖−2u‖=2\sqrt{13}\)

30) \(\displaystyle u=⟨0,1,sinht⟩, v=⟨1,1,0⟩,\) where \(\displaystyle t\) is a real number.

For the following exercises, find the unit vector in the direction of the given vector \(\displaystyle a\) and express it using standard unit vectors.

31) \(\displaystyle a=3i−4j\)

Solution: \(\displaystyle a=\frac{3}{5}i−\frac{4}{5}j\)

32) \(\displaystyle a=⟨4,−3,6⟩\)

33) \(\displaystyle a=\vec{PQ}\), where \(\displaystyle P(−2,3,1)\) and \(\displaystyle Q(0,−4,4)\)

Solution: \(\displaystyle ⟨\frac{2}{\sqrt{62}},−\frac{7}{\sqrt{62}},\frac{3}{\sqrt{62}}⟩\)

34) \(\displaystyle a=\vec{OP},\) where \(\displaystyle P(−1,−1,1)\)

35) \(\displaystyle a=u−v+w,\) where \(\displaystyle u=i−j−k, v=2i−j+k,\) and \(\displaystyle w=−i+j+3k\)

Solution: \(\displaystyle ⟨−\frac{2}{\sqrt{6}},\frac{1}{\sqrt{6}},\frac{1}{\sqrt{6}}⟩\)

36) \(\displaystyle a=2u+v−w,\) where \(\displaystyle u=i−k, v=2j\), and \(\displaystyle w=i−j\)

37) Determine whether \(\displaystyle \vec{AB}\) and \(\displaystyle \vec{PQ}\) are equivalent vectors, where \(\displaystyle A(1,1,1),B(3,3,3),P(1,4,5),\) and \(\displaystyle Q(3,6,7).\)

Solution: Equivalent vectors

38) Determine whether the vectors \(\displaystyle \vec{AB}\) and \(\displaystyle \vec{PQ}\) are equivalent, where \(\displaystyle A(1,4,1), B(−2,2,0), P(2,5,7),\) and \(\displaystyle Q(−3,2,1)\).

For the following exercises, find vector \(\displaystyle u\) with a magnitude that is given and satisfies the given conditions.

39) \(\displaystyle v=⟨7,−1,3⟩, ‖u‖=10,u\) and \(\displaystyle v\) have the same direction

Solution: \(\displaystyle u=⟨\frac{70}{\sqrt{59}},−\frac{10}{\sqrt{59}},\frac{30}{\sqrt{59}}⟩\)

40) \(\displaystyle v=⟨2,4,1⟩, ‖u‖=15,u\) and \(\displaystyle v\) have the same direction

41) \(\displaystyle v=⟨2sint,2cost,1⟩, ‖u‖=2,u\) and \(\displaystyle v\) have opposite directions for any \(\displaystyle t\), where \(\displaystyle t\) is a real number

Solution: \(\displaystyle u=⟨−\frac{4}{\sqrt{5}}sint,−\frac{4}{\sqrt{5}}cost,−\frac{2}{\sqrt{5}}⟩\)

42) \(\displaystyle v=⟨3sinht,0,3⟩, ‖u‖=5,u\) and \(\displaystyle v\) have opposite directions for any \(\displaystyle t\), where \(\displaystyle t\) is a real number

43) Determine a vector of magnitude \(\displaystyle 5\) in the direction of vector \(\displaystyle \vec{AB}\), where \(\displaystyle A(2,1,5)\) and \(\displaystyle B(3,4,−7).\)

Solution: \(\displaystyle ⟨\frac{5}{\sqrt{154}},\frac{15}{\sqrt{154}},−\frac{60}{\sqrt{154}}⟩\)

44) Find a vector of magnitude \(\displaystyle 2\) that points in the opposite direction than vector \(\displaystyle \vec{AB}\), where \(\displaystyle A(−1,−1,1)\) and \(\displaystyle B(0,1,1).\) Express the answer in component form.

45) Consider the points \(\displaystyle A(2,α,0),B(0,1,β),\) and \(\displaystyle C(1,1,β)\), where \(\displaystyle α\) and \(\displaystyle β\) are negative real numbers. Find \(\displaystyle α\) and \(\displaystyle β\) such that \(\displaystyle ∥\vec{OA}−\vec{OB}+\vec{OC}∥=∥\vec{OB}∥=4.\)

Solution: \(\displaystyle α=−\sqrt{7}, β=−\sqrt{15}\)

46) Consider points \(\displaystyle A(α,0,0),B(0,β,0),\) and \(\displaystyle C(α,β,β),\) where \(\displaystyle α\) and \(\displaystyle β\) are positive real numbers. Find \(\displaystyle α\) and \(\displaystyle β\) such that \(\displaystyle ∥\bar{OA}+\bar{OB}∥=\sqrt{2}\) and \(\displaystyle ∥\bar{OC}∥=\sqrt{3}\).

47) Let \(\displaystyle P(x,y,z)\) be a point situated at an equal distance from points \(\displaystyle A(1,−1,0)\) and \(\displaystyle B(−1,2,1)\). Show that point \(\displaystyle P\) lies on the plane of equation \(\displaystyle −2x+3y+z=2.\)

48) Let \(\displaystyle P(x,y,z)\) be a point situated at an equal distance from the origin and point \(\displaystyle A(4,1,2)\). Show that the coordinates of point P satisfy the equation \(\displaystyle 8x+2y+4z=21.\)

49) The points \(\displaystyle A,B,\) and \(\displaystyle C\) are collinear (in this order) if the relation \(\displaystyle ∥\vec{AB}∥+∥\vec{BC}∥=∥\vec{AC}∥\) is satisfied. Show that \(\displaystyle A(5,3,−1),B(−5,−3,1),\) and \(\displaystyle C(−15,−9,3)\) are collinear points.

50) Show that points \(\displaystyle A(1,0,1), B(0,1,1),\) and \(\displaystyle C(1,1,1)\) are not collinear.

51) [T] A force \(\displaystyle F\) of \(\displaystyle 50N\) acts on a particle in the direction of the vector \(\displaystyle \vec{OP}\), where \(\displaystyle P(3,4,0).\)

a. Express the force as a vector in component form.

b. Find the angle between force \(\displaystyle F\) and the positive direction of the x-axis. Express the answer in degrees rounded to the nearest integer.

Solution: \(\displaystyle a. F=⟨30,40,0⟩; b. 53°\)

52) [T] A force \(\displaystyle F\) of \(\displaystyle 40N\) acts on a box in the direction of the vector \(\displaystyle \vec{OP}\), where \(\displaystyle P(1,0,2).\)

a. Express the force as a vector by using standard unit vectors.

b. Find the angle between force \(\displaystyle F\) and the positive direction of the x-axis.

53) If \(\displaystyle F\) is a force that moves an object from point \(\displaystyle P_1(x_1,y_1,z_1)\) to another point \(\displaystyle P_2(x_2,y_2,z_2)\), then the displacement vector is defined as \(\displaystyle D=(x_2−x_1)i+(y_2−y_1)j+(z_2−z_1)k\). A metal container is lifted \(\displaystyle 10\) m vertically by a constant force \(\displaystyle F\). Express the displacement vector \(\displaystyle D\) by using standard unit vectors.

Solution: \(\displaystyle D=10k\)

54) A box is pulled \(\displaystyle 4\) yd horizontally in the x-direction by a constant force \(\displaystyle F\). Find the displacement vector in component form.

55) The sum of the forces acting on an object is called the resultant or net force. An object is said to be in static equilibrium if the resultant force of the forces that act on it is zero. Let \(\displaystyle F_1=⟨10,6,3⟩, F_2=⟨0,4,9⟩\), and \(\displaystyle F_3=⟨10,−3,−9⟩\) be three forces acting on a box. Find the force \(\displaystyle F_4\) acting on the box such that the box is in static equilibrium. Express the answer in component form.

Solution: \(\displaystyle F_4=⟨−20,−7,−3⟩\)

56) [T] Let \(\displaystyle F_k=⟨1,k,k^2⟩, k=1,...,n\) be n forces acting on a particle, with \(\displaystyle n≥2.\)

a. Find the net force \(\displaystyle F=\sum_{k=1}^nF_k.\) Express the answer using standard unit vectors.

b. Use a computer algebra system (CAS) to find n such that \(\displaystyle ∥F∥<100.\)

57) The force of gravity \(\displaystyle F\) acting on an object is given by \(\displaystyle F=mg\), where m is the mass of the object (expressed in kilograms) and \(\displaystyle g\) is acceleration resulting from gravity, with \(\displaystyle ∥g∥=9.8 N/kg.\) A 2-kg disco ball hangs by a chain from the ceiling of a room.

a. Find the force of gravity \(\displaystyle F\) acting on the disco ball and find its magnitude.

b. Find the force of tension \(\displaystyle T\) in the chain and its magnitude.

Express the answers using standard unit vectors.

Figure 18: (credit: modification of work by Kenneth Lu, Flickr)

Solution: \(\displaystyle a. F=−19.6k, ∥F∥=19.6 N; b. T=19.6k, ‖T‖=19.6 N\)

58) A 5-kg pendant chandelier is designed such that the alabaster bowl is held by four chains of equal length, as shown in the following figure.

a. Find the magnitude of the force of gravity acting on the chandelier.

b. Find the magnitudes of the forces of tension for each of the four chains (assume chains are essentially vertical).

59) [T] A 30-kg block of cement is suspended by three cables of equal length that are anchored at points \(\displaystyle P(−2,0,0), Q(1,\sqrt{3},0),\) and \(\displaystyle R(1,−\sqrt{3},0)\). The load is located at \(\displaystyle S(0,0,−2\sqrt{3})\), as shown in the following figure. Let \(\displaystyle F_1, F_2\), and \(\displaystyle F_3\) be the forces of tension resulting from the load in cables \(\displaystyle RS,QS,\) and \(\displaystyle PS,\) respectively.

a. Find the gravitational force \(\displaystyle F\) acting on the block of cement that counterbalances the sum \(\displaystyle F_1+F_2+F_3\) of the forces of tension in the cables.

b. Find forces \(\displaystyle F_1, F_2,\) and \(\displaystyle F_3\). Express the answer in component form.

Solution: a. \(\displaystyle F=−294k\) N; b. \(\displaystyle F_1=⟨−\frac{49\sqrt{3}}{3},49,−98⟩, F_2=⟨−\frac{49\sqrt{3}}{3},−49,−98⟩\), and \(\displaystyle F_3=⟨\frac{98}{\sqrt{3}}{3},0,−98⟩\) (each component is expressed in newtons)

60) Two soccer players are practicing for an upcoming game. One of them runs 10 m from point A to point B. She then turns left at \(\displaystyle 90°\) and runs 10 m until she reaches point C. Then she kicks the ball with a speed of 10 m/sec at an upward angle of \(\displaystyle 45°\) to her teammate, who is located at point A. Write the velocity of the ball in component form.

61) Let \(\displaystyle r(t)=⟨x(t),y(t),z(t)⟩\) be the position vector of a particle at the time \(\displaystyle t∈[0,T]\), where \(\displaystyle x,y,\) and \(\displaystyle z\) are smooth functions on \(\displaystyle [0,T]\). The instantaneous velocity of the particle at time \(\displaystyle t\) is defined by vector \(\displaystyle v(t)=⟨x'(t),y'(t),z'(t)⟩\), with components that are the derivatives with respect to \(\displaystyle t\), of the functions \(\displaystyle x, y\), and \(\displaystyle z\), respectively. The magnitude \(\displaystyle ∥v(t)∥\) of the instantaneous velocity vector is called the speed of the particle at time \(\displaystyle t\). Vector \(\displaystyle a(t)=⟨x''(t),y''(t),z''(t)⟩\), with components that are the second derivatives with respect to \(\displaystyle t\), of the functions \(\displaystyle x,y,\) and \(\displaystyle z\), respectively, gives the acceleration of the particle at time \(\displaystyle t\). Consider \(\displaystyle r(t)=⟨cost,sint,2t⟩\) the position vector of a particle at time \(\displaystyle t∈[0,30],\) where the components of \(\displaystyle r\) are expressed in centimeters and time is expressed in seconds.

a. Find the instantaneous velocity, speed, and acceleration of the particle after the first second. Round your answer to two decimal places.

b. Use a CAS to visualize the path of the particle—that is, the set of all points of coordinates \(\displaystyle (cost,sint,2t),\) where \(\displaystyle t∈[0,30].\)

Solution:

\(\displaystyle a. v(1)=⟨−0.84,0.54,2⟩\) (each component is expressed in centimeters per second); \(\displaystyle ∥v(1)∥=2.24\) (expressed in centimeters per second); \(\displaystyle a(1)=⟨−0.54,−0.84,0⟩\) (each component expressed in centimeters per second squared);

b.

62) [T] Let \(\displaystyle r(t)=⟨t,2t^2,4t^2⟩\) be the position vector of a particle at time \(\displaystyle t\) (in seconds), where \(\displaystyle t∈[0,10]\) (here the components of \(\displaystyle r\) are expressed in centimeters).

a. Find the instantaneous velocity, speed, and acceleration of the particle after the first two seconds. Round your answer to two decimal places.

b. Use a CAS to visualize the path of the particle defined by the points \(\displaystyle (t,2t^2,4t^2),\) where \(\displaystyle t∈[0,60].\)

12.3: The Dot Product

For the following exercises, the vectors \(\displaystyle u\) and \(\displaystyle v\) are given. Calculate the dot product \(\displaystyle u⋅v\).

1) \(\displaystyle u=⟨3,0⟩, v=⟨2,2⟩\)

Solution: 6

2) \(\displaystyle u=⟨3,−4⟩, v=⟨4,3⟩\)

3) \(\displaystyle u=⟨2,2,−1⟩, v=⟨−1,2,2⟩\)

Solution: 0

4) \(\displaystyle u=⟨4,5,−6⟩, v=⟨0,−2,−3⟩\)

For the following exercises, the vectors \(\displaystyle a, b\), and \(\displaystyle c\) are given. Determine the vectors \(\displaystyle (a⋅b)c\) and \(\displaystyle (a⋅c)b.\) Express the vectors in component form.

5) \(\displaystyle a=⟨2,0,−3⟩, b=⟨−4,−7,1⟩, c=⟨1,1,−1⟩\)

Solution: \(\displaystyle (a⋅b)c=⟨−11,−11,11⟩; (a⋅c)b=⟨−20,−35,5⟩\)

6) \(\displaystyle a=⟨0,1,2⟩, b=⟨−1,0,1⟩, c=⟨1,0,−1⟩\)

7) \(\displaystyle a=i+j, b=i−k, c=i−2k\)

Solution: \(\displaystyle (a⋅b)c=⟨1,0,−2⟩; (a⋅c)b=⟨1,0,−1⟩\)

8) \(\displaystyle a=i−j+k, b=j+3k, c=−i+2j−4k\)

For the following exercises, the two-dimensional vectors \(\displaystyle a\) and \(\displaystyle b\) are given.

a. Find the measure of the angle \(\displaystyle θ\) between a and b. Express the answer in radians rounded to two decimal places, if it is not possible to express it exactly.

b. Is \(\displaystyle θ\) an acute angle?

9) [T] \(\displaystyle a=⟨3,−1⟩, b=⟨−4,0⟩\)

Solution: \(\displaystyle a. θ=2.82\)rad; \(\displaystyle b. θ\) is not acute.

10) [T] \(\displaystyle a=⟨2,1⟩, b=⟨−1,3⟩\)

11) \(\displaystyle u=3i, v=4i+4j\)

Solution: \(\displaystyle a. θ=\frac{π}{4}\)rad; \(\displaystyle b. θ\) is acute.

12) \(\displaystyle u=5i, v=−6i+6j\)

For the following exercises, find the measure of the angle between the three-dimensional vectors \(\displaystyle a\) and \(\displaystyle b\). Express the answer in radians rounded to two decimal places, if it is not possible to express it exactly.

13) \(\displaystyle a=⟨3,−1,2⟩, b=⟨1,−1,−2⟩\)

Solution: \(\displaystyle θ=\frac{π}{2}\)

14) \(\displaystyle a=⟨0,−1,−3⟩, b=⟨2,3,−1⟩\)

15) \(\displaystyle a=i+j, b=j−k\)

Solution: \(\displaystyle θ=\frac{π}{3}\)

16) \(\displaystyle a=i−2j+k, b=i+j−2k\)

17) [T] \(\displaystyle a=3i−j−2k, b=v+w,\) where \(\displaystyle v=−2i−3j+2k\) and \(\displaystyle w=i+2k\)

Solution: \(\displaystyle θ=2\)rad

18) [T] \(\displaystyle a=3i−j+2k, b=v−w,\) where \(\displaystyle v=2i+j+4k\) and \(\displaystyle w=6i+j+2k\)

For the following exercises determine whether the given vectors are orthogonal.

19) \(\displaystyle a=⟨x,y⟩, b=⟨−y,x⟩,\) where x and y are nonzero real numbers

Solution: Orthogonal

20) \(\displaystyle a=⟨x,x⟩, b=⟨−y,y⟩,\) where x and y are nonzero real numbers

21) \(\displaystyle a=3i−j−2k, b=−2i−3j+k\)

Solution: Not orthogonal

22) \(\displaystyle a=i−j, b=7i+2j−k\)

23) Find all two-dimensional vectors a orthogonal to vector \(\displaystyle b=⟨3,4⟩.\) Express the answer in component form.

Solution: \(\displaystyle a=⟨−\frac{4α}{3},α⟩,\) where \(\displaystyle α≠0\) is a real number

24) Find all two-dimensional vectors \(\displaystyle a\) orthogonal to vector \(\displaystyle b=⟨5,−6⟩.\) Express the answer by using standard unit vectors.

25) Determine all three-dimensional vectors \(\displaystyle u\) orthogonal to vector \(\displaystyle v=⟨1,1,0⟩.\) Express the answer by using standard unit vectors.

Solution: \(\displaystyle u=−αi+αj+βk,\) where \(\displaystyle α\) and \(\displaystyle β\) are real numbers such that \(\displaystyle α^2+β^2≠0\)

26) Determine all three-dimensional vectors \(\displaystyle u\) orthogonal to vector \(\displaystyle v=i−j−k.\) Express the answer in component form.

27) Determine the real number \(\displaystyle α\) such that vectors \(\displaystyle a=2i+3j\) and \(\displaystyle b=9i+αj\) are orthogonal.

Solution: \(\displaystyle α=−6\)

28) Determine the real number \(\displaystyle α\) such that vectors \(\displaystyle a=−3i+2j\) and \(\displaystyle b=2i+αj\) are orthogonal.

29) [T] Consider the points \(\displaystyle P(4,5)\) and \(\displaystyle Q(5,−7)\).

a. Determine vectors \(\displaystyle \vec{OP}\) and \(\displaystyle \vec{OQ}\). Express the answer by using standard unit vectors.

b. Determine the measure of angle O in triangle OPQ. Express the answer in degrees rounded to two decimal places.

Solution: \(\displaystyle a. \vec{OP}→=4i+5j, \vec{OQ}=5i−7j; b. 105.8°\)

30) [T] Consider points \(\displaystyle A(1,1), B(2,−7),\) and \(\displaystyle C(6,3)\).

a. Determine vectors \(\displaystyle \vec{BA}\) and \(\displaystyle \vec{BC}\). Express the answer in component form.

b. Determine the measure of angle B in triangle ABC. Express the answer in degrees rounded to two decimal places.

31) Determine the measure of angle A in triangle ABC, where \(\displaystyle A(1,1,8), B(4,−3,−4),\) and \(\displaystyle C(−3,1,5).\) Express your answer in degrees rounded to two decimal places.

Solution: \(\displaystyle 68.33°\)

32) Consider points \(\displaystyle P(3,7,−2)\) and \(\displaystyle Q(1,1,−3).\) Determine the angle between vectors \(\displaystyle \vec{OP}\) and \(\displaystyle \vec{OQ}\). Express the answer in degrees rounded to two decimal places.

For the following exercises, determine which (if any) pairs of the following vectors are orthogonal.

33) \(\displaystyle u=⟨3,7,−2⟩, v=⟨5,−3,−3⟩, w=⟨0,1,−1⟩\)

Solution: \(\displaystyle u\) and \(\displaystyle v\) are orthogonal; \(\displaystyle v\) and \(\displaystyle w\) are orthogonal.

34) \(\displaystyle u=i−k, v=5j−5k, w=10j\)

35) Use vectors to show that a parallelogram with equal diagonals is a rectangle.

36) Use vectors to show that the diagonals of a rhombus are perpendicular.

37) Show that \(\displaystyle u⋅(v+w)=u⋅v+u⋅w\) is true for any vectors \(\displaystyle u, v\), and \(\displaystyle w\).

38) Verify the identity \(\displaystyle u⋅(v+w)=u⋅v+u⋅w\) for vectors \(\displaystyle u=⟨1,0,4⟩, v=⟨−2,3,5⟩,\) and \(\displaystyle w=⟨4,−2,6⟩.\)

For the following problems, the vector \(\displaystyle u\) is given.

a. Find the direction cosines for the vector u.

b. Find the direction angles for the vector u expressed in degrees. (Round the answer to the nearest integer.)

39) \(\displaystyle u=⟨2,2,1⟩\)

Solution: \(\displaystyle a. cosα=\frac{2}{3},cosβ=\frac{2}{3},\) and \(\displaystyle cosγ=\frac{1}{3}; b. α=48°, β=48°,\) and \(\displaystyle γ=71°\)

40) \(\displaystyle u=i−2j+2k\)

41) \(\displaystyle u=⟨−1,5,2⟩\)

Solution: \(\displaystyle a. cosα=−\frac{1}{\sqrt{30}},cosβ=\frac{5}{\sqrt{30}},\) and \(\displaystyle cosγ=\frac{2}{\sqrt{30}}; b. α=101°, β=24°,\) and \(\displaystyle γ=69°\)

42) \(\displaystyle u=⟨2,3,4⟩\)

43) Consider \(\displaystyle u=⟨a,b,c⟩\) a nonzero three-dimensional vector. Let \(\displaystyle cosα, cosβ,\) and \(\displaystyle cosγ\) be the directions of the cosines of \(\displaystyle u\). Show that \(\displaystyle cos^2α+cos^2β+cos^2γ=1.\)

44) Determine the direction cosines of vector \(\displaystyle u=i+2j+2k\) and show they satisfy \(\displaystyle cos^2α+cos^2β+cos^2γ=1.\)

of vector v into the orthogonal components w and q, where w is the projection of v onto u and q is a vector orthogonal to the direction of u.

For the following exercises, the vectors \(\displaystyle u\) and \(\displaystyle v\) are given.

a. Find the vector projection \(\displaystyle w=proj_uv\) of vector \(\displaystyle v\) onto vector \(\displaystyle u\). Express your answer in component form.

b. Find the scalar projection \(\displaystyle comp_uv\) of vector \(\displaystyle v\) onto vector \(\displaystyle u\).

45) \(\displaystyle u=5i+2j, v=2i+3j\)

Solution: \(\displaystyle a. w=⟨\frac{80}{29},\frac{32}{29}⟩; b. comp_uv=\frac{16}{\sqrt{29}}\)

46) \(\displaystyle u=⟨−4,7⟩, v=⟨3,5⟩\)

47) \(\displaystyle u=3i+2k, v=2j+4k\)

Solution: \(\displaystyle a. w=⟨\frac{24}{13},0,\frac{16}{13}⟩; b. comp_uv=\frac{8}{\sqrt{13}}\)

48) \(\displaystyle u=⟨4,4,0⟩, v=⟨0,4,1⟩\)

49) Consider the vectors \(\displaystyle u=4i−3j\) and \(\displaystyle v=3i+2j.\)

a. Find the component form of vector \(\displaystyle w=proj_uv\) that represents the projection of \(\displaystyle v\) onto \(\displaystyle u\).

b. Write the decomposition \(\displaystyle v=w+q\) of vector \(\displaystyle v\) into the orthogonal components \(\displaystyle w\) and \(\displaystyle q\), where \(\displaystyle w\) is the projection of \(\displaystyle v\) onto \(\displaystyle u\) and \(\displaystyle q\) is a vector orthogonal to the direction of \(\displaystyle u\).

Solution: \(\displaystyle a. w=⟨\frac{24}{25},−\frac{18}{25}⟩; b. q=⟨\frac{51}{25},\frac{68}{25}⟩, v=w+q=⟨\frac{24}{25},−\frac{18}{25}⟩+⟨\frac{51}{25},\frac{68}{25}⟩\)

50) Consider vectors \(\displaystyle u=2i+4j\) and \(\displaystyle v=4j+2k.\)

a. Find the component form of vector \(\displaystyle w=proj_uv\) 0that represents the projection of \(\displaystyle v\) onto \(\displaystyle u\).

b. Write the decomposition \(\displaystyle v=w+q\) of vector \(\displaystyle v\) into the orthogonal components \(\displaystyle w\) and \(\displaystyle q\), where \(\displaystyle w\) is the projection of \(\displaystyle v\) onto \(\displaystyle u\) and \(\displaystyle q\) is a vector orthogonal to the direction of \(\displaystyle u\).

51) A methane molecule has a carbon atom situated at the origin and four hydrogen atoms located at points \(\displaystyle P(1,1,−1),Q(1,−1,1),R(−1,1,1),\) and \(\displaystyle S(−1,−1,−1)\) (see figure).

a. Find the distance between the hydrogen atoms located at P and R.

b. Find the angle between vectors \(\displaystyle \vec{OS}\) and \(\displaystyle \vec{OR}\) that connect the carbon atom with the hydrogen atoms located at S and R, which is also called the bond angle. Express the answer in degrees rounded to two decimal places.

Solution: \(\displaystyle a. 2\sqrt{2}; b. 109.47°\)

52) [T] Find the vectors that join the center of a clock to the hours 1:00, 2:00, and 3:00. Assume the clock is circular with a radius of 1 unit.

53) Find the work done by force \(\displaystyle F=⟨5,6,−2⟩\) (measured in Newtons) that moves a particle from point \(\displaystyle P(3,−1,0)\) to point \(\displaystyle Q(2,3,1)\) along a straight line (the distance is measured in meters).

Solution: \(\displaystyle 17N⋅m\)

54) [T] A sled is pulled by exerting a force of 100 N on a rope that makes an angle of \(\displaystyle 25°\) with the horizontal. Find the work done in pulling the sled 40 m. (Round the answer to one decimal place.)

55) [T] A father is pulling his son on a sled at an angle of \(\displaystyle 20°\)with the horizontal with a force of 25 lb (see the following image). He pulls the sled in a straight path of 50 ft. How much work was done by the man pulling the sled? (Round the answer to the nearest integer.)

Solution: 1175 ft⋅lb

56) [T] A car is towed using a force of 1600 N. The rope used to pull the car makes an angle of 25° with the horizontal. Find the work done in towing the car 2 km. Express the answer in joules \(\displaystyle (1J=1N⋅m)\) rounded to the nearest integer.

57) [T] A boat sails north aided by a wind blowing in a direction of \(\displaystyle N30°E\) with a magnitude of 500 lb. How much work is performed by the wind as the boat moves 100 ft? (Round the answer to two decimal places.)

Answer

\(25000\sqrt{3}\) ft-lbs \(\approx 43,301.27\) ft-lbs

Solution:

Vector representing the wind: \(\vecs w = 500\cos 60^{\circ} \mathbf{\hat i} + 500\sin 60^{\circ} \mathbf{\hat j}\)
Vector representing the displacement to the north: \(\vecs d = 100 \mathbf{\hat j}\)
Work done by the wind: \(W = \vecs w \cdot \vecs d = 25000\sqrt{3}\) ft-lbs \(\approx 43,301.27\) ft-lbs

58) Vector \(\displaystyle p=⟨150,225,375⟩\) represents the price of certain models of bicycles sold by a bicycle shop. Vector \(\displaystyle n=⟨10,7,9⟩\) represents the number of bicycles sold of each model, respectively. Compute the dot product \(\displaystyle p⋅n\) and state its meaning.

59) [T] Two forces \(\displaystyle F_1\) and \(\displaystyle F_2\) are represented by vectors with initial points that are at the origin. The first force has a magnitude of 20 lb and the terminal point of the vector is point \(\displaystyle P(1,1,0)\). The second force has a magnitude of 40 lb and the terminal point of its vector is point \(\displaystyle Q(0,1,1)\). Let F be the resultant force of forces \(\displaystyle F_1\) and \(\displaystyle F_2\).

a. Find the magnitude of \(\displaystyle F\). (Round the answer to one decimal place.)

b. Find the direction angles of \(\displaystyle F\). (Express the answer in degrees rounded to one decimal place.)

Solution: \(\displaystyle a. ∥F_1+F_2∥=52.9\) lb; b. The direction angles are \(\displaystyle α=74.5°,β=36.7°,\) and \(\displaystyle γ=57.7°.\)

60) [T] Consider \(\displaystyle r(t)=⟨cost,sint,2t⟩\) the position vector of a particle at time \(\displaystyle t∈[0,30]\), where the components of \(\displaystyle r\) are expressed in centimeters and time in seconds. Let \(\displaystyle \vec{OP}\) be the position vector of the particle after 1 sec.

a. Show that all vectors \(\displaystyle \vec{PQ}\), where \(\displaystyle Q(x,y,z)\) is an arbitrary point, orthogonal to the instantaneous velocity vector v(1) of the particle after 1 sec, can be expressed as \(\displaystyle \vec{PQ}=⟨x−cos1,y−sin1,z−2⟩\), where \(\displaystyle xsin1−ycos1−2z+4=0.\) The set of point Q describes a plane called the normal plane to the path of the particle at point P.

b. Use a CAS to visualize the instantaneous velocity vector and the normal plane at point P along with the path of the particle.

12.4: The Cross Product

For the following exercises, the vectors \(\displaystyle u\) and \(\displaystyle v\) are given.

a. Find the cross product \(\displaystyle u×v\) of the vectors \(\displaystyle u\) and \(\displaystyle v\). Express the answer in component form.

b. Sketch the vectors \(\displaystyle u,v,\) and \(\displaystyle u×v.\)

1) \(\displaystyle u=⟨2,0,0⟩, v=⟨2,2,0⟩\)

Solution:

\(\displaystyle a. u×v=⟨0,0,4⟩;\)

b.

2) \(\displaystyle u=⟨3,2,−1⟩, v=⟨1,1,0⟩\)

3) \(\displaystyle u=2i+3j, v=j+2k\)

Solution:

a. \(\displaystyle a. u×v=⟨6,−4,2⟩;\)

b.

4) \(\displaystyle u=2j+3k, v=3i+k\)

5) Simplify \(\displaystyle (i×i−2i×j−4i×k+3j×k)×i.\)

Solution: \(\displaystyle −2j−4k\)

6) Simplify \(\displaystyle j×(k×j+2j×i−3j×j+5i×k).\)

In the following exercises, vectors \(\displaystyle u\) and \(\displaystyle v\) are given. Find unit vector \(\displaystyle w\) in the direction of the cross product vector \(\displaystyle u×v.\) Express your answer using standard unit vectors.

7) \(\displaystyle u=⟨3,−1,2⟩, v=⟨−2,0,1⟩\)

Solution: \(\displaystyle w=−\frac{1}{3\sqrt{6}}i−\frac{7}{3\sqrt{6}}j−\frac{2}{3\sqrt{6}}k\)

8) \(\displaystyle u=⟨2,6,1⟩, v=⟨3,0,1⟩\)

9) \(\displaystyle u=\vec{AB}, v=\vec{AC},\) where \(\displaystyle A(1,0,1), B(1,−1,3)\), and \(\displaystyle C(0,0,5)\)

Solution: \(\displaystyle w=−\frac{4}{\sqrt{21}}i−\frac{2}{\sqrt{21}}j−\frac{1}{\sqrt{21}}k\)

10) \(\displaystyle u=\vec{OP}, v=\vec{PQ},\) where \(\displaystyle P(−1,1,0)\) and \(\displaystyle Q(0,2,1)\)

11) Determine the real number \(\displaystyle α\) such that \(\displaystyle u×v\) and \(\displaystyle i\) are orthogonal, where \(\displaystyle u=3i+j−5k\) and \(\displaystyle v=4i−2j+αk.\)

Solution: \(\displaystyle α=10\)

12) Show that \(\displaystyle u×v\) and \(\displaystyle 2i−14j+2k\) cannot be orthogonal for any α real number, where \(\displaystyle u=i+7j−k\) and \(\displaystyle v=αi+5j+k\).

13) Show that \(\displaystyle u×v\) is orthogonal to \(\displaystyle u+v\) and \(\displaystyle u−v\), where \(\displaystyle u\) and \(\displaystyle v\) are nonzero vectors.

14) Show that \(\displaystyle v×u\) is orthogonal to \(\displaystyle (u⋅v)(u+v)+u\), where \(\displaystyle u\) and \(\displaystyle v\) are nonzero vectors.

15) Calculate the determinant \(\displaystyle \begin{bmatrix}i&j&K\\1&&−1&7\\2&0&3\end{bmatrix}\).

Solution: \(\displaystyle −3i+11j+2k\)

16) Calculate the determinant \(\displaystyle \begin{bmatrix}i&j&K\\0&3&−4\\1&6&−1\end{bmatrix}\).

For the following exercises, the vectors \(\displaystyle u\) and \(\displaystyle v\) are given. Use determinant notation to find vector \(\displaystyle w\) orthogonal to vectors \(\displaystyle u\) and \(\displaystyle v\).

17) \(\displaystyle u=⟨−1,0,e^t⟩, v=⟨1,e^{−t},0⟩,\) where \(\displaystyle t\) is a real number

Solution: \(\displaystyle w=⟨−1,e^t,−e^{−t}⟩\)

18) \(\displaystyle u=⟨1,0,x⟩, v=⟨\frac{2}{x},1,0⟩,\) where \(\displaystyle x\) is a nonzero real number

19) Find vector \(\displaystyle (a−2b)×c,\) where \(\displaystyle a=\begin{bmatrix}i&j&k\\2&−1&5\\0&1&8\end{bmatrix}, b=\begin{bmatrix}i&j&K\\0&1&1\\2&−1&−2\end{bmatrix},\) and \(\displaystyle c=i+j+k.\)

Solution: \(\displaystyle −26i+17j+9k\)

20) Find vector \(\displaystyle c×(a+3b),\) where \(\displaystyle a=\begin{bmatrix}i&j&K\\5&0&9\\0&1&0\end{bmatrix}, b=\begin{bmatrix}i&j&k\\0&−1&1\\7&1&−1\end{bmatrix},\) and \(\displaystyle c=i−k.\)

21) [T] Use the cross product \(\displaystyle u×v\) to find the acute angle between vectors \(\displaystyle u\) and \(\displaystyle v\), where \(\displaystyle u=i+2j\) and \(\displaystyle v=i+k.\) Express the answer in degrees rounded to the nearest integer.

Solutuion: \(\displaystyle 72°\)

22) [T] Use the cross product \(\displaystyle u×v\) to find the obtuse angle between vectors \(\displaystyle u\) and \(\displaystyle v\), where \(\displaystyle u=−i+3j+k\) and \(\displaystyle v=i−2j.\) Express the answer in degrees rounded to the nearest integer.

23) Use the sine and cosine of the angle between two nonzero vectors \(\displaystyle u\) and \(\displaystyle v\) to prove Lagrange’s identity: \(\displaystyle ‖u×v‖^2=‖u‖^2‖v‖^2−(u⋅v)^2\).

24) Verify Lagrange’s identity \(\displaystyle ‖u×v‖^2=‖u‖^2‖v‖^2−(u⋅v)^2\) for vectors \(\displaystyle u=−i+j−2k\) and \(\displaystyle v=2i−j.\)

25) Nonzero vectors \(\displaystyle u\) and \(\displaystyle v\) are called collinear if there exists a nonzero scalar \(\displaystyle α\) such that \(\displaystyle v=αu\). Show that \(\displaystyle u\) and \(\displaystyle v\) are collinear if and only if \(\displaystyle u×v=0.\)

26) Nonzero vectors \(\displaystyle u\) and \(\displaystyle v\) are called collinear if there exists a nonzero scalar \(\displaystyle α\) such that \(\displaystyle v=αu\). Show that vectors \(\displaystyle \vec{AB}\) and \(\displaystyle \vec{AC}\) are collinear, where \(\displaystyle A(4,1,0), B(6,5,−2),\) and \(\displaystyle C(5,3,−1).\)

27) Find the area of the parallelogram with adjacent sides \(\displaystyle u=⟨3,2,0⟩\) and \(\displaystyle v=⟨0,2,1⟩\).

Solution: \(\displaystyle 7\)

28) Find the area of the parallelogram with adjacent sides \(\displaystyle u=i+j\) and \(\displaystyle v=i+k.\)

29) Consider points \(\displaystyle A(3,−1,2),B(2,1,5),\) and \(\displaystyle C(1,−2,−2).\)

a. Find the area of parallelogram ABCD with adjacent sides \(\displaystyle \vec{AB}\) and \(\displaystyle \vec{AC}\).

b. Find the area of triangle ABC.

c. Find the distance from point A to line BC.

Solution: \(\displaystyle a. 5\sqrt{6}; b. \frac{5\sqrt{6}}{2}; c. \frac{5\sqrt{6}}{\sqrt{59}}\)

30) Consider points \(\displaystyle A(2,−3,4),B(0,1,2),\) and \(\displaystyle C(−1,2,0).\)

a. Find the area of parallelogram ABCD with adjacent sides \(\displaystyle \vec{AB}\) and \(\displaystyle \vec{AC}\).

b. Find the area of triangle ABC.

c. Find the distance from point B to line AC.

In the following exercises, vectors \(\displaystyle u,v\), and \(\displaystyle w\) are given.

a. Find the triple scalar product \(\displaystyle u⋅(v×w).\)

b. Find the volume of the parallelepiped with the adjacent edges \(\displaystyle u,v\), and \(\displaystyle w\).

31) \(\displaystyle u=i+j, v=j+k,\) and \(\displaystyle w=i+k\)

Solution: \(\displaystyle a. 2; b. 2\)

32) \(\displaystyle u=⟨−3,5,−1⟩, v=⟨0,2,−2⟩,\) and \(\displaystyle w=⟨3,1,1⟩\)

33) Calculate the triple scalar products \(\displaystyle v⋅(u×w)\) and \(\displaystyle w⋅(u×v),\) where \(\displaystyle u=⟨1,1,1⟩, v=⟨7,6,9⟩,\) and \(\displaystyle w=⟨4,2,7⟩.\)

Solution: \(\displaystyle v⋅(u×w)=−1, w⋅(u×v)=1\)

34) Calculate the triple scalar products \(\displaystyle w⋅(v×u)\) and \(\displaystyle u⋅(w×v),\) where \(\displaystyle u=⟨4,2,−1⟩, v=⟨2,5,−3⟩,\) and \(\displaystyle w=⟨9,5,−10⟩.\)

35) Find vectors \(\displaystyle a,b\), and \(\displaystyle c\) with a triple scalar product given by the determinant \(\displaystyle \begin{bmatrix}1&2&3\\0&2&5\\8&9&2\end{bmatrix}\). Determine their triple scalar product.

Solution: \(\displaystyle a=⟨1,2,3⟩, b=⟨0,2,5⟩, c=⟨8,9,2⟩; a⋅(b×c)=−9\)

36) The triple scalar product of vectors \(\displaystyle a,b,\) and \(\displaystyle c\) is given by the determinant \(\displaystyle \begin{bmatrix}0&−2&1\\0&1&4\\1&−3&7\end{bmatrix}\). Find vector \(\displaystyle a−b+c.\)

37) Consider the parallelepiped with edges \(\displaystyle OA,OB,\) and \(\displaystyle OC\), where \(\displaystyle A(2,1,0),B(1,2,0),\) and \(\displaystyle C(0,1,α).\)

a. Find the real number \(\displaystyle α>0\) such that the volume of the parallelepiped is \(\displaystyle 3\) units^3.

b. For \(\displaystyle α=1,\) find the height \(\displaystyle h\) from vertex \(\displaystyle C\) of the parallelepiped. Sketch the parallelepiped.

Solution: \(\displaystyle a. α=1; b. h=1,\)

38) Consider points \(\displaystyle A(α,0,0),B(0,β,0),\) and \(\displaystyle C(0,0,γ)\), with \(\displaystyle α, β\), and \(\displaystyle γ\) positive real numbers.

a. Determine the volume of the parallelepiped with adjacent sides \(\displaystyle \vec{OA}, \vec{OB},\) and \(\displaystyle \vec{OC}\).

b. Find the volume of the tetrahedron with vertices \(\displaystyle O,A,B,\) and \(\displaystyle C\). (Hint: The volume of the tetrahedron is \(\displaystyle 1/6\) of the volume of the parallelepiped.)

c. Find the distance from the origin to the plane determined by \(\displaystyle A,B,\) and \(\displaystyle C\). Sketch the parallelepiped and tetrahedron.

39) Let \(\displaystyle u,v,\) and \(\displaystyle w\) be three-dimensional vectors and c be a real number. Prove the following properties of the cross product.

a. \(\displaystyle u×u=0\)

b. \(\displaystyle u×(v+w)=(u×v)+(u×w)\)

c. \(\displaystyle c(u×v)=(cu)×v=u×(cv)\)

d. \(\displaystyle u⋅(u×v)=0\)

40) Show that vectors \(\displaystyle u=⟨1,0,−8⟩, v=⟨0,1,6⟩,\) and \(\displaystyle w=⟨−1,9,3⟩\) satisfy the following properties of the cross product.

a. \(\displaystyle u×u=0\)

b. \(\displaystyle u×(v+w)=(u×v)+(u×w)\)

c. \(\displaystyle c(u×v)=(cu)×v=u×(cv)\)

d. \(\displaystyle u⋅(u×v)=0\)

41) Nonzero vectors \(\displaystyle u,v,\) and \(\displaystyle w\) are said to be linearly dependent if one of the vectors is a linear combination of the other two. For instance, there exist two nonzero real numbers \(\displaystyle α\) and \(\displaystyle β\) such that \(\displaystyle w=αu+βv\). Otherwise, the vectors are called linearly independent. Show that \(\displaystyle u,v,\) and \(\displaystyle w\) are coplanar if and only if they are linear dependent.

42) Consider vectors \(\displaystyle u=⟨1,4,−7⟩, v=⟨2,−1,4⟩, w=⟨0,−9,18⟩,\) and \(\displaystyle p=⟨0,−9,17⟩.\)

a. Show that \(\displaystyle u,v,\) and \(\displaystyle w\) are coplanar by using their triple scalar product

b. Show that \(\displaystyle u,v,\) and \(\displaystyle w\) are coplanar, using the definition that there exist two nonzero real numbers \(\displaystyle α\) and \(\displaystyle β\) such that \(\displaystyle w=αu+βv.\)

c. Show that \(\displaystyle u,v,\) and \(\displaystyle p\) are linearly independent—that is, none of the vectors is a linear combination of the other two.

43) Consider points \(\displaystyle A(0,0,2), B(1,0,2), C(1,1,2),\) and \(\displaystyle D(0,1,2).\) Are vectors \(\displaystyle \vec{AB}, \vec{AC},\) and \(\displaystyle \vec{AD}\) linearly dependent (that is, one of the vectors is a linear combination of the other two)?

Solution: Yes, \(\displaystyle \vec{AD}=α\vec{AB}+β\vec{AC},\) where \(\displaystyle α=−1\) and \(\displaystyle β=1.\)

44) Show that vectors \(\displaystyle i+j, i−j,\) and \(\displaystyle i+j+k\) are linearly independent—that is, there exist two nonzero real numbers \(\displaystyle α\) and \(\displaystyle β\) such that \(\displaystyle i+j+k=α(i+j)+β(i−j).\)

45) Let \(\displaystyle u=⟨u_1,u_2⟩\) and \(\displaystyle v=⟨v_1,v_2⟩\) be two-dimensional vectors. The cross product of vectors \(\displaystyle u\) and \(\displaystyle v\) is not defined. However, if the vectors are regarded as the three-dimensional vectors \(\displaystyle \tilde{u}=⟨u_1,u_2,0⟩\) and \(\displaystyle \tilde{v}=⟨v_1,v_2,0⟩\), respectively, then, in this case, we can define the cross product of \(\displaystyle \tilde{u}\) and \(\displaystyle \tilde{v}\). In particular, in determinant notation, the cross product of \(\displaystyle \tilde{u}\) and \(\displaystyle \tilde{v}\) is given by

\(\displaystyle \tilde{u}×\tilde{v}=\begin{bmatrix}i&j&k\\u_1&u_2&0\\v_1&v_2&0\end{bmatrix}\).

Use this result to compute \(\displaystyle (icosθ+jsinθ)×(isinθ−jcosθ),\) where \(\displaystyle θ\) is a real number.

Solution: \(\displaystyle −k\)

46) Consider points \(\displaystyle P(2,1), Q(4,2),\) and \(\displaystyle R(1,2).\)

a. Find the area of triangle \(\displaystyle P,Q,\) and \(\displaystyle R.\)

b. Determine the distance from point \(\displaystyle R\) to the line passing through \(\displaystyle P\) and \(\displaystyle Q\).

47) Determine a vector of magnitude \(\displaystyle 10\) perpendicular to the plane passing through the x-axis and point \(\displaystyle P(1,2,4).\)

Solution: \(\displaystyle ⟨0,±4\sqrt{5},2\sqrt{5}⟩\)

48) Determine a unit vector perpendicular to the plane passing through the z-axis and point \(\displaystyle A(3,1,−2).\)

49) Consider \(\displaystyle u\) and \(\displaystyle v\) two three-dimensional vectors. If the magnitude of the cross product vector \(\displaystyle u×v\) is \(\displaystyle k\) times larger than the magnitude of vector \(\displaystyle u\), show that the magnitude of \(\displaystyle v\) is greater than or equal to \(\displaystyle k\), where \(\displaystyle k\) is a natural number.

50) [T] Assume that the magnitudes of two nonzero vectors \(\displaystyle u\) and \(\displaystyle v\) are known. The function \(\displaystyle f(θ)=‖u‖‖v‖sinθ\) defines the magnitude of the cross product vector \(\displaystyle u×v,\) where \(\displaystyle θ∈[0,π]\) is the angle between \(\displaystyle u\) and \(\displaystyle v\).

a. Graph the function \(\displaystyle f\).

b. Find the absolute minimum and maximum of function \(\displaystyle f\). Interpret the results.

c. If \(\displaystyle ‖u‖=5\) and \(\displaystyle ‖v‖=2\), find the angle between \(\displaystyle u\) and \(\displaystyle v\) if the magnitude of their cross product vector is equal to \(\displaystyle 9\).

51) Find all vectors \(\displaystyle w=⟨w_1,w_2,w_3⟩\) that satisfy the equation \(\displaystyle ⟨1,1,1⟩×w=⟨−1,−1,2⟩.\)

Solution: \(\displaystyle w=⟨w_3−1,w_3+1,w_3⟩,\) where \(\displaystyle w_3\) is any real number

52) Solve the equation \(\displaystyle w×⟨1,0,−1⟩=⟨3,0,3⟩,\) where \(\displaystyle w=⟨w_1,w_2,w_3⟩\) is a nonzero vector with a magnitude of \(\displaystyle 3\).

53) [T] A mechanic uses a 12-in. wrench to turn a bolt. The wrench makes a \(\displaystyle 30°\) angle with the horizontal. If the mechanic applies a vertical force of \(\displaystyle 10\) lb on the wrench handle, what is the magnitude of the torque at point \(\displaystyle P\) (see the following figure)? Express the answer in foot-pounds rounded to two decimal places.

Solution: 8.66 ft-lb

54) [T] A boy applies the brakes on a bicycle by applying a downward force of 20 lb on the pedal when the 6-in. crank makes a \(\displaystyle 40°\) angle with the horizontal (see the following figure). Find the torque at point \(\displaystyle P\). Express your answer in foot-pounds rounded to two decimal places.

55) [T] Find the magnitude of the force that needs to be applied to the end of a 20-cm wrench located on the positive direction of the y-axis if the force is applied in the direction \(\displaystyle ⟨0,1,−2⟩\) and it produces a \(\displaystyle 100\) N·m torque to the bolt located at the origin.

Solution: 250 N

56) [T] What is the magnitude of the force required to be applied to the end of a 1-ft wrench at an angle of \(\displaystyle 35°\) to produce a torque of \(\displaystyle 20\) N·m?

57) [T] The force vector \(\displaystyle F\) acting on a proton with an electric charge of \(\displaystyle 1.6×10^{−19}C\) (in coulombs) moving in a magnetic field \(\displaystyle B\) where the velocity vector \(\displaystyle v\) is given by \(\displaystyle F=1.6×10^{−19}(v×B)\) (here, \(\displaystyle v\) is expressed in meters per second, \(\displaystyle B\) is in tesla [T], and \(\displaystyle F\) is in newtons [N]). Find the force that acts on a proton that moves in the xy-plane at velocity \(\displaystyle v=10^5i+10^5j\) (in meters per second) in a magnetic field given by \(\displaystyle B=0.3j\).

Solution: \(\displaystyle F=4.8×10^{−15}kN\)

58) [T] The force vector \(\displaystyle F\) acting on a proton with an electric charge of \(\displaystyle 1.6×10^{−19}C\) moving in a magnetic field \(\displaystyle B\) where the velocity vector \(\displaystyle v\) is given by \(\displaystyle F=1.6×10^{−19}(v×B)\) (here, \(\displaystyle v\) is expressed in meters per second, \(\displaystyle B\) in \(\displaystyle T\), and \(\displaystyle F\) in \(\displaystyle N\)). If the magnitude of force \(\displaystyle F\) acting on a proton is \(\displaystyle 5.9×10^{−17} N\) and the proton is moving at the speed of 300 m/sec in magnetic field \(\displaystyle B\) of magnitude 2.4 T, find the angle between velocity vector \(\displaystyle v\) of the proton and magnetic field \(\displaystyle B\). Express the answer in degrees rounded to the nearest integer.

60) [T] Consider \(\displaystyle r(t)=⟨cost,sint,2t⟩\) the position vector of a particle at time \(\displaystyle t∈[0,30]\), where the components of \(\displaystyle r\) are expressed in centimeters and time in seconds. Let \(\displaystyle \vec{OP}\) be the position vector of the particle after \(\displaystyle 1\) sec.

a. Determine unit vector \(\displaystyle B(t)\) (called the binormal unit vector) that has the direction of cross product vector \(\displaystyle v(t)×a(t),\) where \(\displaystyle v(t)\) and \(\displaystyle a(t)\) are the instantaneous velocity vector and, respectively, the acceleration vector of the particle after \(\displaystyle t\) seconds.

b. Use a CAS to visualize vectors \(\displaystyle v(1), a(1),\) and \(\displaystyle B(1)\) as vectors starting at point \(\displaystyle P\) along with the path of the particle.

Solution:

\(\displaystyle a. B(t)=⟨\frac{2sint}{\sqrt{5}},−\frac{2cost}{\sqrt{5}},\frac{1}{\sqrt{5}}⟩;\)

b.

61) A solar panel is mounted on the roof of a house. The panel may be regarded as positioned at the points of coordinates (in meters) \(\displaystyle A(8,0,0), B(8,18,0), C(0,18,8),\) and \(\displaystyle D(0,0,8)\) (see the following figure).

a. Find vector \(\displaystyle n=\vec{AB}×\vec{AD}\) perpendicular to the surface of the solar panels. Express the answer using standard unit vectors.

b. Assume unit vector \(\displaystyle s=\frac{1}{\sqrt{3}}i+\frac{1}{\sqrt{3}}j+\frac{1}{\sqrt{3}}k\) points toward the Sun at a particular time of the day and the flow of solar energy is \(\displaystyle F=900s\) (in watts per square meter [\(\displaystyle W/m^2\)]). Find the predicted amount of electrical power the panel can produce, which is given by the dot product of vectors \(\displaystyle F\) and \(\displaystyle n\) (expressed in watts).

c. Determine the angle of elevation of the Sun above the solar panel. Express the answer in degrees rounded to the nearest whole number. (Hint: The angle between vectors \(\displaystyle n\) and \(\displaystyle s\) and the angle of elevation are complementary.)

12.5: Equations of Lines and Planes in Space

In the following exercises, points \(\displaystyle P\) and \(\displaystyle Q\) are given. Let \(\displaystyle L\) be the line passing through points \(\displaystyle P\) and \(\displaystyle Q\).

a. Find the vector equation of line \(\displaystyle L\).

b. Find parametric equations of line \(\displaystyle L\).

c. Find symmetric equations of line \(\displaystyle L\).

d. Find parametric equations of the line segment determined by \(\displaystyle P\) and \(\displaystyle Q\).

1) \(\displaystyle P(−3,5,9), Q(4,−7,2)\)

Solution: \(\displaystyle a. r=⟨−3,5,9⟩+t⟨7,−12,−7⟩, t∈R; b. x=−3+7t,y=5−12t,z=9−7t, t∈R; c. \frac{x+3}{7}=\frac{y−5}{−12}=\frac{z−9}{−7}; d. x=−3+7t,y=5−12t,z=9−7t, t∈[0,1]\)

2) \(\displaystyle P(4,0,5),Q(2,3,1)\)

3) \(\displaystyle P(−1,0,5), Q(4,0,3)\)

Solution: \(\displaystyle a. r=⟨−1,0,5⟩+t⟨5,0,−2⟩, t∈R; b. x=−1+5t,y=0,z=5−2t, t∈R; c. \frac{x+1}{5}=\frac{z−5}{−2},y=0; d. x=−1+5t,y=0,z=5−2t, t∈[0,1]\)

4) \(\displaystyle P(7,−2,6), Q(−3,0,6)\)

For the following exercises, point \(\displaystyle P\) and vector \(\displaystyle v\) are given. Let \(\displaystyle L\) be the line passing through point \(\displaystyle P\) with direction \(\displaystyle v\).

a. Find parametric equations of line \(\displaystyle L\).

b. Find symmetric equations of line \(\displaystyle L\).

c. Find the intersection of the line with the xy-plane.

5) \(\displaystyle P(1,−2,3), v=⟨1,2,3⟩\)

Solution: \(\displaystyle a. x=1+t,y=−2+2t,z=3+3t, t∈R; b. \frac{x−1}{1}=\frac{y+2}{2}=\frac{z−3}{3}; c. (0,−4,0)\)

6) \(\displaystyle P(3,1,5), v=⟨1,1,1⟩\)

7) \(\displaystyle P(3,1,5), v=\vec{QR},\) where \(\displaystyle Q(2,2,3)\) and \(\displaystyle R(3,2,3)\)

Solution: \(\displaystyle a. x=3+t,y=1,z=5, t∈R; b. y=1,z=5;\) c. The line does not intersect the xy-plane.

8) \(\displaystyle P(2,3,0), v=\vec{QR},\) where \(\displaystyle Q(0,4,5)\) and \(\displaystyle R(0,4,6)\)

For the following exercises, line \(\displaystyle L\) is given.

a. Find point \(\displaystyle P\) that belongs to the line and direction vector \(\displaystyle v\) of the line. Express \(\displaystyle v\) in component form.

b. Find the distance from the origin to line \(\displaystyle L\).

9) \(\displaystyle x=1+t,y=3+t,z=5+4t, t∈R\)

Solution: \(\displaystyle a. P(1,3,5), v=⟨1,1,4⟩; b. \sqrt{3}\)

10) \(\displaystyle −x=y+1,z=2\)

Find the distance between point \(\displaystyle A(−3,1,1)\) and the line of symmetric equations

11) \(\displaystyle x=−y=−z.\)

Solution: \(\displaystyle \frac{2\sqrt{2}}{\sqrt{3}}\)

Find the distance between point \(\displaystyle A(4,2,5)\) and the line of parametric equations

12) \(\displaystyle x=−1−t,y=−t,z=2, t∈R.\)

For the following exercises, lines \(\displaystyle L_1\) and \(\displaystyle L_2\) are given.

a. Verify whether lines \(\displaystyle L_1\) and \(\displaystyle L_2\) are parallel.

b. If the lines \(\displaystyle L_1\) and \(\displaystyle L_2\) are parallel, then find the distance between them.

13) \(\displaystyle L_1:x=1+t,y=t,z=2+t, t∈R, L_2:x−3=y−1=z−3\)

Solution: a. Parallel; b. \(\displaystyle \frac{\sqrt{2}}{\sqrt{3}}\)

14) \(\displaystyle L_1:x=2,y=1,z=t, L_2:x=1,y=1,z=2−3t, t∈R\)

15) Show that the line passing through points \(\displaystyle P(3,1,0)\) and \(\displaystyle Q(1,4,−3)\) is perpendicular to the line with equation \(\displaystyle x=3t,y=3+8t,z=−7+6t, t∈R.\)

16) Are the lines of equations \(\displaystyle x=−2+2t,y=−6,z=2+6t\) and \(\displaystyle x=−1+t,y=1+t,z=t, t∈R,\) perpendicular to each other?

17) Find the point of intersection of the lines of equations \(\displaystyle x=−2y=3z\) and \(\displaystyle x=−5−t,y=−1+t,z=t−11, t∈R.\)

Solution: \(\displaystyle (−12,6,−4)\)

18) Find the intersection point of the x-axis with the line of parametric equations \(\displaystyle x=10+t,y=2−2t,z=−3+3t,

t∈R.\)

For the following exercises, lines \(\displaystyle L_1\) and \(\displaystyle L_2\) are given. Determine whether the lines are equal, parallel but not equal, skew, or intersecting.

19) \(\displaystyle L_1:x=y−1=−z\) and \(\displaystyle L_2:x−2=−y=\frac{z}{2}\)

Solution: The lines are skew.

20) \(\displaystyle L_1:x=2t,y=0,z=3, t∈R\) and \(\displaystyle L_2:x=0,y=8+s,z=7+s, s∈R\)

21) \(\displaystyle L_1:x=−1+2t,y=1+3t,z=7t, t∈R\) and \(\displaystyle L_2:x−1=\frac{2}{3}(y−4)=\frac{2}{7}z−2\)

Solution: The lines are equal.

22) \(\displaystyle L_1:3x=y+1=2z\) and \(\displaystyle L_2:x=6+2t,y=17+6t,z=9+3t, t∈R\)

23) Consider line \(\displaystyle L\) of symmetric equations \(\displaystyle x−2=−y=\frac{z}{2}\) and point \(\displaystyle A(1,1,1).\)

a. Find parametric equations for a line parallel to \(\displaystyle L\) that passes through point \(\displaystyle A\).

b. Find symmetric equations of a line skew to \(\displaystyle L\) and that passes through point \(\displaystyle A\).

c. Find symmetric equations of a line that intersects \(\displaystyle L\) and passes through point \(\displaystyle A\).

Solution: \(\displaystyle a. x=1+t,y=1−t,z=1+2t, t∈R;\) b. For instance, the line passing through \(\displaystyle A\) with direction vector \(\displaystyle j:x=1,z=1;\) c. For instance, the line passing through \(\displaystyle A\) and point \(\displaystyle (2,0,0)\) that belongs to \(\displaystyle L\) is a line that intersects; \(\displaystyle L:\frac{x−1}{−1}=y−1=z−1\)

24) Consider line \(\displaystyle L\) of parametric equations \(\displaystyle x=t,y=2t,z=3, t∈R.\)

a. Find parametric equations for a line parallel to \(\displaystyle L\) that passes through the origin.

b. Find parametric equations of a line skew to \(\displaystyle L\) that passes through the origin.

c. Find symmetric equations of a line that intersects \(\displaystyle L\) and passes through the origin.

For the following exercises, point \(\displaystyle P\) and vector \(\displaystyle n\) are given.

a. Find the scalar equation of the plane that passes through \(\displaystyle P\) and has normal vector \(\displaystyle n\).

b. Find the general form of the equation of the plane that passes through \(\displaystyle P\) and has normal vector \(\displaystyle n\).

25) \(\displaystyle P(0,0,0), n=3i−2j+4k\)

Solution: \(\displaystyle a. 3x−2y+4z=0; b. 3x−2y+4z=0\)

26) \(\displaystyle P(3,2,2), n=2i+3j−k\)

27) \(\displaystyle P(1,2,3), n=⟨1,2,3⟩\)

Solution: \(\displaystyle a. (x−1)+2(y−2)+3(z−3)=0; b. x+2y+3z−14=0\)

28) \(\displaystyle P(0,0,0), n=⟨−3,2,−1⟩\)

For the following exercises, the equation of a plane is given.

a. Find normal vector \(\displaystyle n\) to the plane. Express \(\displaystyle n\) using standard unit vectors.

b. Find the intersections of the plane with the axes of coordinates.

c. Sketch the plane.

29) [T] \(\displaystyle 4x+5y+10z−20=0\)

Solution:

\(\displaystyle a. n=4i+5j+10k; b. (5,0,0), (0,4,0),\) and \(\displaystyle (0,0,2);\)

c.

30) \(\displaystyle 3x+4y−12=0\)

31) \(\displaystyle 3x−2y+4z=0\)

Solution:

\(\displaystyle a. n=3i−2j+4k; b. (0,0,0);\)

c.

32) \(\displaystyle x+z=0\)

33) Given point \(\displaystyle P(1,2,3)\) and vector \(\displaystyle n=i+j\), find point \(\displaystyle Q\) on the x-axis such that \(\displaystyle \vec{PQ}\) and \(\displaystyle n\) are orthogonal.

Solution: \(\displaystyle (3,0,0)\)

34) Show there is no plane perpendicular to \(\displaystyle n=i+j\) that passes through points \(\displaystyle P(1,2,3)\) and \(\displaystyle Q(2,3,4)\).

35) Find parametric equations of the line passing through point \(\displaystyle P(−2,1,3)\) that is perpendicular to the plane of equation \(\displaystyle 2x−3y+z=7.\)

Solution: \(\displaystyle x=−2+2t,y=1−3t,z=3+t, t∈R\)

36) Find symmetric equations of the line passing through point \(\displaystyle P(2,5,4)\) that is perpendicular to the plane of equation \(\displaystyle 2x+3y−5z=0.\)

37) Show that line \(\displaystyle \frac{x−1}{2}=\frac{y+1}{3}=\frac{z−2}{4}\) is parallel to plane \(\displaystyle x−2y+z=6\).

38) Find the real number \(\displaystyle α\) such that the line of parametric equations \(\displaystyle x=t,y=2−t,z=3+t, t∈R\) is parallel to the plane of equation \(\displaystyle αx+5y+z−10=0.\)

For the following exercises, the equations of two planes are given.

a. Determine whether the planes are parallel, orthogonal, or neither.

b. If the planes are neither parallel nor orthogonal, then find the measure of the angle between the planes. Express the answer in degrees rounded to the nearest integer.

39) [T] \(\displaystyle x+y+z=0, 2x−y+z−7=0\)

Solution: a. The planes are neither parallel nor orthogonal; b. \(\displaystyle 62°\)

40) \(\displaystyle 5x−3y+z=4, x+4y+7z=1\)

41) \(\displaystyle x−5y−z=1, 5x−25y−5z=−3\)

Solution: a. The planes are parallel.

42) [T] \(\displaystyle x−3y+6z=4, 5x+y−z=4\)

43) Show that the lines of equations \(\displaystyle x=t,y=1+t,z=2+t, t∈R,\) and \(\displaystyle \frac{x}{2}=\frac{y−1}{3}=z−3\) are skew, and find the distance between them.

Solution: \(\displaystyle \frac{1}{\sqrt{6}}\)

44) Show that the lines of equations \(\displaystyle x=−1+t,y=−2+t,z=3t, t∈R,\) and \(\displaystyle x=5+s,y=−8+2s,z=7s, s∈R\) are skew, and find the distance between them.

45) Consider point \(\displaystyle C(−3,2,4)\) and the plane of equation \(\displaystyle 2x+4y−3z=8\).

a. Find the radius of the sphere with center \(\displaystyle C\) tangent to the given plane.

b. Find point P of tangency.

Solution: \(\displaystyle a. \frac{18}{\sqrt{29}}; b. P(−\frac{51}{29},\frac{130}{29},\frac{62}{29})\)

46) Consider the plane of equation \(\displaystyle x−y−z−8=0.\)

a. Find the equation of the sphere with center \(\displaystyle C\) at the origin that is tangent to the given plane.

b. Find parametric equations of the line passing through the origin and the point of tangency.

47) Two children are playing with a ball. The girl throws the ball to the boy. The ball travels in the air, curves \(\displaystyle 3\) ft to the right, and falls \(\displaystyle 5\) ft away from the girl (see the following figure). If the plane that contains the trajectory of the ball is perpendicular to the ground, find its equation.

Solution: \(\displaystyle 4x−3y=0\)

48) [T] John allocates \(\displaystyle d\) dollars to consume monthly three goods of prices \(\displaystyle a,b\), and \(\displaystyle c\). In this context, the budget equation is defined as \(\displaystyle ax+by+cz=d,\) where \(\displaystyle x≥0,y≥0\), and \(\displaystyle z≥0\) represent the number of items bought from each of the goods. The budget set is given by \(\displaystyle {(x,y,z)|ax+by+cz≤d,x≥0,y≥0,z≥0},\) and the budget plane is the part of the plane of equation \(\displaystyle ax+by+cz=d\) for which \(\displaystyle x≥0,y≥0\), and \(\displaystyle z≥0\). Consider \(\displaystyle a=$8, b=$5, c=$10,\) and \(\displaystyle d=$500.\)

a. Use a CAS to graph the budget set and budget plane.

b. For \(\displaystyle z=25,\) find the new budget equation and graph the budget set in the same system of coordinates.

49) [T] Consider \(\displaystyle r(t)=⟨sint,cost,2t⟩\) the position vector of a particle at time \(\displaystyle t∈[0,3]\), where the components of \(\displaystyle r\) are expressed in centimeters and time is measured in seconds. Let \(\displaystyle \vec{OP}\) be the position vector of the particle after \(\displaystyle 1\) sec.

a. Determine the velocity vector \(\displaystyle v(1)\) of the particle after \(\displaystyle 1\) sec.

b. Find the scalar equation of the plane that is perpendicular to \(\displaystyle v(1)\) and passes through point \(\displaystyle P\). This plane is called the normal plane to the path of the particle at point \(\displaystyle P\).

c. Use a CAS to visualize the path of the particle along with the velocity vector and normal plane at point \(\displaystyle P\).

Solution: \(\displaystyle a. v(1)=⟨cos1,−sin1,2⟩; b. (cos1)(x−sin1)−(sin1)(y−cos1)+2(z−2)=0;\)

c.

50) [T] A solar panel is mounted on the roof of a house. The panel may be regarded as positioned at the points of coordinates (in meters) \(\displaystyle A(8,0,0), B(8,18,0), C(0,18,8),\) and \(\displaystyle D(0,0,8)\) (see the following figure).

a. Find the general form of the equation of the plane that contains the solar panel by using points \(\displaystyle A,B,\) and \(\displaystyle C\), and show that its normal vector is equivalent to \(\displaystyle \vec{AB}×\vec{AD}.\)

b. Find parametric equations of line \(\displaystyle L_1\) that passes through the center of the solar panel and has direction vector \(\displaystyle s=\frac{1}{\sqrt{3}}i+\frac{1}{\sqrt{3}}j+\frac{1}{\sqrt{3}}k,\) which points toward the position of the Sun at a particular time of day.

c. Find symmetric equations of line \(\displaystyle L_2\) that passes through the center of the solar panel and is perpendicular to it.

d. Determine the angle of elevation of the Sun above the solar panel by using the angle between lines \(\displaystyle L_1\) and \(\displaystyle L_2\).

12.6: Quadric Surfaces

For the following exercises, sketch and describe the cylindrical surface of the given equation.

1) [T] \(\displaystyle x^2+z^2=1\)

Solution: The surface is a cylinder with the rulings parallel to the y-axis.

2) [T] \(\displaystyle x^2+y^2=9\)

3) [T] \(\displaystyle z=cos(\frac{π}{2}+x)\)

Solution: The surface is a cylinder with rulings parallel to the y-axis.

4) [T] \(\displaystyle z=e^x\)

5) [T] \(\displaystyle z=9−y^2\)

Solution: The surface is a cylinder with rulings parallel to the x-axis.

6) [T] \(\displaystyle z=ln(x)\)

For the following exercises, the graph of a quadric surface is given.

a. Specify the name of the quadric surface.

b. Determine the axis of symmetry of the quadric surface.

7)

Solution: a. Cylinder; b. The x-axis

8)

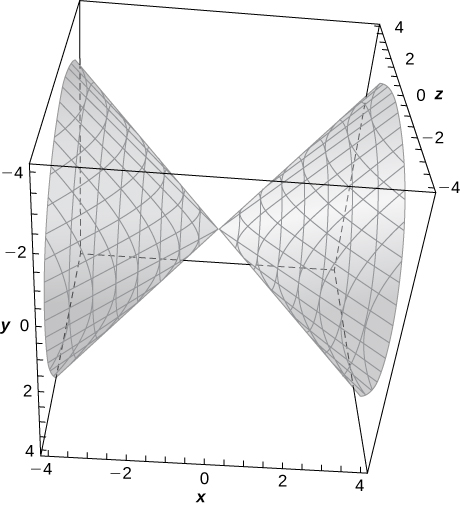
9)

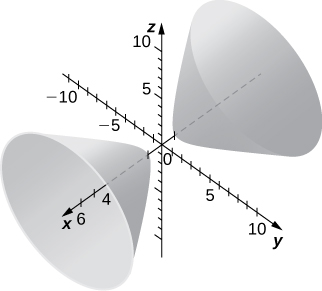
Solution: a. Hyperboloid of two sheets; b. The x-axis

10)

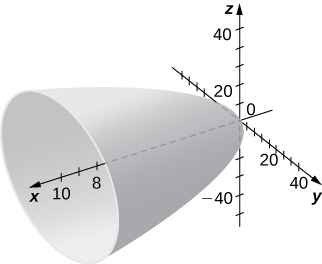
For the following exercises, match the given quadric surface with its corresponding equation in standard form.

a. \(\displaystyle \frac{x^2}{4}+\frac{y^2}{9}−\frac{z^2}{12}=1\)

b. \(\displaystyle \frac{x^2}{4}−\frac{y^2}{9}−\frac{z^2}{12}=1\)

c. \(\displaystyle \frac{x^2}{4}+\frac{y^2}{9}+\frac{z^2}{12}=1\)

d. \(\displaystyle z^2=4x^2+3y^2\)

e. \(\displaystyle z=4x^2−y^2\)

f. \(\displaystyle 4x^2+y^2−z^2=0\)

11) Hyperboloid of two sheets

Solution: b.

12) Ellipsoid

13) Elliptic paraboloid

Solution: d.

14) Hyperbolic paraboloid

15) Hyperboloid of one sheet

Solution: a.

16) Elliptic cone

For the following exercises, rewrite the given equation of the quadric surface in standard form. Identify the surface.

17) \(\displaystyle −x^2+36y^2+36z^2=9\)

Solution: \(\displaystyle −\frac{x^2}{9}+\frac{y^2}{\frac{1}{4}}+\frac{z^2}{\frac{1}{4}}=1,\) hyperboloid of one sheet with the x-axis as its axis of symmetry

18) \(\displaystyle −4x^2+25y^2+z^2=100\)

19) \(\displaystyle −3x^2+5y^2−z^2=10\)

Solution: \(\displaystyle −\frac{x^2}{\frac{10}{3}}+\frac{y^2}{2}−\frac{z^2}{10}=1,\) hyperboloid of two sheets with the y-axis as its axis of symmetry

20) \(\displaystyle 3x^2−y^2−6z^2=18\)

21) \(\displaystyle 5y=x^2−z^2\)

Solution: \(\displaystyle y=−\frac{z^2}{5}+\frac{x^2}{5},\) hyperbolic paraboloid with the y-axis as its axis of symmetry

22) \(\displaystyle 8x^2−5y^2−10z=0\)

23) \(\displaystyle x^2+5y^2+3z^2−15=0\)

Solurion: \(\displaystyle \frac{x^2}{15}+\frac{y^2}{3}+\frac{z^2}{5}=1,\) ellipsoid

24) \(\displaystyle 63x^2+7y^2+9z^2−63=0\)

25) \(\displaystyle x^2+5y^2−8z^2=0\)

Solution: \(\displaystyle \frac{x^2}{40}+\frac{y^2}{8}−\frac{z^2}{5}=0,\) elliptic cone with the z-axis as its axis of symmetry

26) \(\displaystyle 5x^2−4y^2+20z^2=0\)

27) \(\displaystyle 6x=3y^2+2z^2\)

Solution: \(\displaystyle x=\frac{y^2}{2}+\frac{z^2}{3},\) elliptic paraboloid with the x-axis as its axis of symmetry

28) \(\displaystyle 49y=x^2+7z^2\)

For the following exercises, find the trace of the given quadric surface in the specified plane of coordinates and sketch it.

29) [T] \(\displaystyle x^2+z^2+4y=0,z=0\)

Solution: Parabola \(\displaystyle y=−\frac{x^2}{4},\)

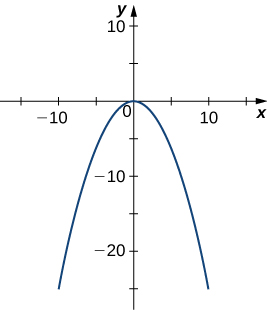
30) [T] \(\displaystyle x^2+z^2+4y=0,x=0\)

31) [T] \(\displaystyle −4x^2+25y^2+z^2=100,x=0\)

Solution: Ellipse \(\displaystyle \frac{y^2}{4}+\frac{z^2}{100}=1,\)

32) [T] \(\displaystyle −4x^2+25y^2+z^2=100,y=0\)

33) [T] \(\displaystyle x^2+\frac{y^2}{4}+\frac{z^2}{100}=1,x=0\)

Solution: Ellipse \(\displaystyle \frac{y^2}{4}+\frac{z^2}{100}=1,\)

34) [T] \(\displaystyle x^2−y−z^2=1,y=0\)

35) Use the graph of the given quadric surface to answer the questions.

a. Specify the name of the quadric surface.

b. Which of the equations—\(\displaystyle 16x^2+9y^2+36z^2=3600,9x^2+36y^2+16z^2=3600,\) or \(\displaystyle 36x^2+9y^2+16z^2=3600\) —corresponds to the graph?

c. Use b. to write the equation of the quadric surface in standard form.

Solution: a. Ellipsoid; b. The third equation; c. \(\displaystyle \frac{x^2}{100}+\frac{y^2}{400}+\frac{z^2}{225}=1\)

36) Use the graph of the given quadric surface to answer the questions.

a. Specify the name of the quadric surface.

b. Which of the equations—\(\displaystyle 36z=9x^2+y^2,9x^2+4y^2=36z\), or \(\displaystyle −36z=−81x^2+4y^2\) —corresponds to the graph above?

c. Use b. to write the equation of the quadric surface in standard form.

For the following exercises, the equation of a quadric surface is given.

a. Use the method of completing the square to write the equation in standard form.

b. Identify the surface.

37) \(\displaystyle x^2+2z^2+6x−8z+1=0\)

Solution: \(\displaystyle a. \frac{(x+3)^2}{16}+\frac{(z−2)^2}{8}=1;\) b. Cylinder centered at \(\displaystyle (−3,2)\) with rulings parallel to the y-axis

38) \(\displaystyle 4x^2−y^2+z^2−8x+2y+2z+3=0\)

39) \(\displaystyle x^2+4y^2−4z^2−6x−16y−16z+5=0\)

Solution: \(\displaystyle a. \frac{(x−3)^2}{4}+(y−2)^2−(z+2)^2=1;\) b. Hyperboloid of one sheet centered at \(\displaystyle (3,2,−2),\) with the z-axis as its axis of symmetry

40) \(\displaystyle x^2+z^2−4y+4=0\)

41) \(\displaystyle x^2+\frac{y^2}{4}−\frac{z^2}{3}+6x+9=0\)

Solution: \(\displaystyle a. (x+3)^2+\frac{y^2}{4}−\frac{z^2}{3}=0;\) b. Elliptic cone centered at \(\displaystyle (−3,0,0),\) with the z-axis as its axis of symmetry

42) \(\displaystyle x^2−y^2+z^2−12z+2x+37=0\)

43) Write the standard form of the equation of the ellipsoid centered at the origin that passes through points \(\displaystyle A(2,0,0),B(0,0,1),\) and \(\displaystyle C(12,\sqrt{11},\frac{1}{2}).\)

Solution: \(\displaystyle \frac{x^2}{4}+\frac{y^2}{16}+z^2=1\)

44) Write the standard form of the equation of the ellipsoid centered at point \(\displaystyle P(1,1,0)\) that passes through points \(\displaystyle A(6,1,0),B(4,2,0)\) and \(\displaystyle C(1,2,1)\).

45) Determine the intersection points of elliptic cone \(\displaystyle x^2−y^2−z^2=0\) with the line of symmetric equations \(\displaystyle \frac{x−1}{2}=\frac{y+1}{3}=z.\)

Solution: \(\displaystyle (1,−1,0)\) and \(\displaystyle (\frac{13}{3},4,\frac{5}{3})\)

46) Determine the intersection points of parabolic hyperboloid \(\displaystyle z=3x^2−2y^2\) with the line of parametric equations \(\displaystyle x=3t,y=2t,z=19t\), where \(\displaystyle t∈R.\)

47) Find the equation of the quadric surface with points \(\displaystyle P(x,y,z)\) that are equidistant from point \(\displaystyle Q(0,−1,0)\) and plane of equation \(\displaystyle y=1.\) Identify the surface.

Solution: \(\displaystyle x^2+z^2+4y=0,\) elliptic paraboloid

48) Find the equation of the quadric surface with points \(\displaystyle P(x,y,z)\) that are equidistant from point \(\displaystyle Q(0,2,0)\) and plane of equation \(\displaystyle y=−2.\) Identify the surface.

49) If the surface of a parabolic reflector is described by equation \(\displaystyle 400z=x^2+y^2,\) find the focal point of the reflector.

Solution: \(\displaystyle (0,0,100)\)

50) Consider the parabolic reflector described by equation \(\displaystyle z=20x^2+20y^2.\) Find its focal point.

51) Show that quadric surface \(\displaystyle x^2+y^2+z^2+2xy+2xz+2yz+x+y+z=0\) reduces to two parallel planes.

52) Show that quadric surface \(\displaystyle x^2+y^2+z^2−2xy−2xz+2yz−1=0\) reduces to two parallel planes passing.

53) [T] The intersection between cylinder \(\displaystyle (x−1)^2+y^2=1\) and sphere \(\displaystyle x^2+y^2+z^2=4\) is called a Viviani curve.

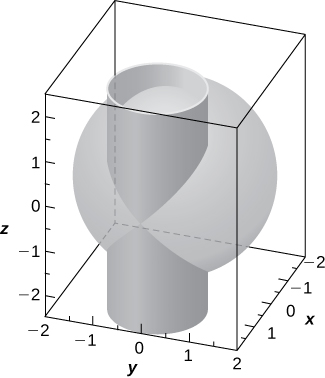
a. Solve the system consisting of the equations of the surfaces to find the equation of the intersection curve. (Hint: Find \(\displaystyle x\) and \(\displaystyle y\) in terms of \(\displaystyle z\).)

b. Use a computer algebra system (CAS) to visualize the intersection curve on sphere \(\displaystyle x^2+y^2+z^2=4\).

Solution: \(\displaystyle a. x=2−\frac{z^2}{2},y=±\frac{z}{2}\sqrt{4−z^2},\) where \(\displaystyle z∈[−2,2];\)

b.

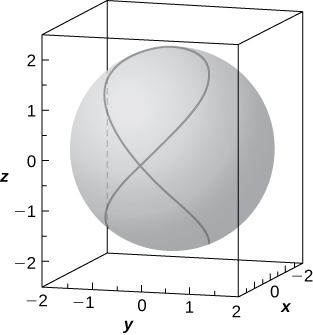
54) Hyperboloid of one sheet \(\displaystyle 25x^2+25y^2−z^2=25\) and elliptic cone \(\displaystyle −25x^2+75y^2+z^2=0\) are represented in the following figure along with their intersection curves. Identify the intersection curves and find their equations (Hint: Find y from the system consisting of the equations of the surfaces.)

55) [T] Use a CAS to create the intersection between cylinder \(\displaystyle 9x^2+4y^2=18\) and ellipsoid \(\displaystyle 36x^2+16y^2+9z^2=144\), and find the equations of the intersection curves.

Solution: two ellipses of equations \(\displaystyle \frac{x^2}{2}+\frac{y^2}{\frac{9}{2}}=1\) in planes \(\displaystyle z=±2\sqrt{2}\)

56) [T] A spheroid is an ellipsoid with two equal semiaxes. For instance, the equation of a spheroid with the z-axis as its axis of symmetry is given by \(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{a^2}+\frac{z^2}{c^2}=1\), where \(\displaystyle a\) and \(\displaystyle c\) are positive real numbers. The spheroid is called oblate if \(\displaystyle c<a\), and prolate for \(\displaystyle c>a\).

a. The eye cornea is approximated as a prolate spheroid with an axis that is the eye, where \(\displaystyle a=8.7mm\) and \(\displaystyle c=9.6mm\).Write the equation of the spheroid that models the cornea and sketch the surface.

b. Give two examples of objects with prolate spheroid shapes.

57) [T] In cartography, Earth is approximated by an oblate spheroid rather than a sphere. The radii at the equator and poles are approximately \(\displaystyle 3963\)mi and \(\displaystyle 3950\)mi, respectively.

a. Write the equation in standard form of the ellipsoid that represents the shape of Earth. Assume the center of Earth is at the origin and that the trace formed by plane \(\displaystyle z=0\) corresponds to the equator.

b. Sketch the graph.

c. Find the equation of the intersection curve of the surface with plane \(\displaystyle z=1000\) that is parallel to the xy-plane. The intersection curve is called a parallel.

d. Find the equation of the intersection curve of the surface with plane \(\displaystyle x+y=0\) that passes through the z-axis. The intersection curve is called a meridian.

Solution:

\(\displaystyle a. \frac{x^2}{3963^2}+\frac{y^2}{3963^2}+\frac{z^2}{3950^2}=1;\)

b.

c. The intersection curve is the ellipse of equation \(\displaystyle \frac{x^2}{3963^2}+\frac{y^2}{3963^2}=\frac{(2950)(4950)}{3950^2}\), and the intersection is an ellipse.; d. The intersection curve is the ellipse of equation \(\displaystyle \frac{2y^2}{3963^2}+\frac{z^2}{3950^2}=1.\)

58) [T] A set of buzzing stunt magnets (or “rattlesnake eggs”) includes two sparkling, polished, superstrong spheroid-shaped magnets well-known for children’s entertainment. Each magnet is \(\displaystyle 1.625\) in. long and \(\displaystyle 0.5\) in. wide at the middle. While tossing them into the air, they create a buzzing sound as they attract each other.

a. Write the equation of the prolate spheroid centered at the origin that describes the shape of one of the magnets.

b. Write the equations of the prolate spheroids that model the shape of the buzzing stunt magnets. Use a CAS to create the graphs.

59) [T] A heart-shaped surface is given by equation \(\displaystyle (x^2+\frac{9}{4}y^2+z^2−1)^3−x^2z^3−\frac{9}{80}y^2z^3=0.\)

a. Use a CAS to graph the surface that models this shape.

b. Determine and sketch the trace of the heart-shaped surface on the xz-plane.

Solution:

a.

b. The intersection curve is \(\displaystyle (x^2+z^2−1)^3−x^2z^3=0.\)

60) [T] The ring torus symmetric about the z-axis is a special type of surface in topology and its equation is given by \(\displaystyle (x^2+y^2+z^2+R^2−r^2)^2=4R^2(x^2+y^2)\), where \(\displaystyle R>r>0\). The numbers \(\displaystyle R\) and \(\displaystyle r\) are called are the major and minor radii, respectively, of the surface. The following figure shows a ring torus for which \(\displaystyle R=2\) and \(\displaystyle r=1\).

a. Write the equation of the ring torus with \(\displaystyle R=2\) and \(\displaystyle r=1\), and use a CAS to graph the surface. Compare the graph with the figure given.

b. Determine the equation and sketch the trace of the ring torus from a. on the xy-plane.

c. Give two examples of objects with ring torus shapes.

12.7: Cylindrical and Spherical Coordinates

Use the following figure as an aid in identifying the relationship between the rectangular, cylindrical, and spherical coordinate systems.

For the following exercises, the cylindrical coordinates \(\displaystyle (r,θ,z)\) of a point are given. Find the rectangular coordinates \(\displaystyle (x,y,z)\) of the point.

1) \(\displaystyle (4,\frac{π}{6},3)\)

Solution: \(\displaystyle (2\sqrt{3},2,3)\)

2) \(\displaystyle (3,\frac{π}{3},5)\)

3) \(\displaystyle (4,\frac{7π}{6},3)\)

Solution: \(\displaystyle −2\sqrt{3},−2,3)\)

4) \(\displaystyle (2,π,−4)\)

For the following exercises, the rectangular coordinates \(\displaystyle (x,y,z)\) of a point are given. Find the cylindrical coordinates \(\displaystyle (r,θ,z)\)of the point.

5) \(\displaystyle (1,\sqrt{3},2)\)

Solution: \(\displaystyle (2,\frac{π}{3},2)\)

6) \(\displaystyle (1,1,5)\)

7) \(\displaystyle (3,−3,7)\)

Solution: \(\displaystyle (3\sqrt{2},−\frac{π}{4},7)\)

8) \(\displaystyle (−2\sqrt{2},2\sqrt{2},4)\)

For the following exercises, the equation of a surface in cylindrical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

9) [T] \(\displaystyle r=4\)

Solution: A cylinder of equation \(\displaystyle x^2+y^2=16,\) with its center at the origin and rulings parallel to the z-axis,

10) [T] \(\displaystyle z=r^2cos^2θ\)

11) [T] \(\displaystyle r^2cos(2θ)+z^2+1=0\)

Solution: Hyperboloid of two sheets of equation \(\displaystyle −x^2+y^2−z^2=1,\) with the y-axis as the axis of symmetry,

12) [T] \(\displaystyle r=3sinθ\)

13) [T] \(\displaystyle r=2cosθ\)

Solution: Cylinder of equation \(\displaystyle x^2−2x+y^2=0,\) with a center at \(\displaystyle (1,0,0)\) and radius \(\displaystyle 1\), with rulings parallel to the z-axis,

14) [T] \(\displaystyle r^2+z^2=5\)

15) [T] \(\displaystyle r=2secθ\)

Solution: Plane of equation \(\displaystyle x=2,\)

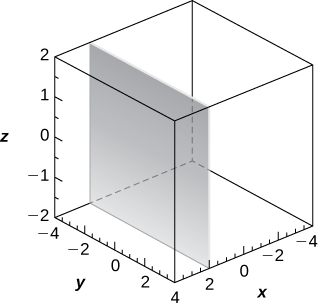
16) [T] \(\displaystyle r=3cscθ\)

For the following exercises, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in cylindrical coordinates.

17) \(\displaystyle z=3\)

Solution: \(\displaystyle z=3\)

18) \(\displaystyle x=6\)

19) \(\displaystyle x^2+y^2+z^2=9\)

Solution: \(\displaystyle r^2+z^2=9\)

20) \(\displaystyle y=2x^2\)

21) \(\displaystyle x^2+y^2−16x=0\)

Solution: \(\displaystyle r=16cosθ,r=0\)

22) \(\displaystyle x^2+y^2−3\sqrt{x^2+y^2}+2=0\)

For the following exercises, the spherical coordinates \(\displaystyle (ρ,θ,φ)\) of a point are given. Find the rectangular coordinates \(\displaystyle (x,y,z)\) of the point.

23) \(\displaystyle (3,0,π)\)

Solution: \(\displaystyle (0,0,−3)\)

24) \(\displaystyle (1,\frac{π}{6},\frac{π}{6})\)

25) \(\displaystyle (12,−\frac{π}{4},\frac{π}{4})\)

Solution: \(\displaystyle (6,−6,\sqrt{2})\)

26) \(\displaystyle (3,\frac{π}{4},\frac{π}{6})\)

For the following exercises, the rectangular coordinates \(\displaystyle (x,y,z)\) of a point are given. Find the spherical coordinates \(\displaystyle (ρ,θ,φ)\) of the point. Express the measure of the angles in degrees rounded to the nearest integer.

27) \(\displaystyle (4,0,0)\)

Solution: \(\displaystyle (4,0,90°)\)

28) \(\displaystyle (−1,2,1)\)

29) \(\displaystyle (0,3,0)\)

Solution: \(\displaystyle (3,90°,90°)\)

30) \(\displaystyle (−2,2\sqrt{3},4)\)

For the following exercises, the equation of a surface in spherical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.

31) [T] \(\displaystyle ρ=3\)

Solution: Sphere of equation \(\displaystyle x^2+y^2+z^2=9\) centered at the origin with radius \(\displaystyle 3\),

32) [T] \(\displaystyle φ=\frac{π}{3}\)

33) [T] \(\displaystyle ρ=2cosφ\)

Solution: Sphere of equation \(\displaystyle x^2+y^2+(z−1)^2=1\) centered at \(\displaystyle (0,0,1)\) with radius \(\displaystyle 1\),

34) [T] \(\displaystyle ρ=4cscφ\)

35) [T] \(\displaystyle φ=\frac{π}{2}\)

Solution: The xy-plane of equation \(\displaystyle z=0,\)

36) [T] \(\displaystyle ρ=6cscφsecθ\)

For the following exercises, the equation of a surface in rectangular coordinates is given. Find the equation of the surface in spherical coordinates. Identify the surface.

37) \(\displaystyle x^2+y^2−3z^2=0, z≠0\)

Solution: \(\displaystyle φ=\frac{π}{3}\) or \(\displaystyle φ=\frac{2π}{3};\) Elliptic cone

38) \(\displaystyle x^2+y^2+z^2−4z=0\)

39) \(\displaystyle z=6\)

Solution: \(\displaystyle ρcosφ=6;\) Plane at \(\displaystyle z=6\)

40) \(\displaystyle x^2+y^2=9\)

For the following exercises, the cylindrical coordinates of a point are given. Find its associated spherical coordinates, with the measure of the angle φ

in radians rounded to four decimal places.

41) [T] \(\displaystyle (1,\frac{π}{4},3)\)

Solution: \(\displaystyle (\sqrt{10},\frac{π}{4},0.3218)\)

42) [T] \(\displaystyle (5,π,12)\)

43) \(\displaystyle (3,\frac{π}{2},3)\)

Solution: \(\displaystyle (3\sqrt{2},\frac{π}{2},\frac{π}{4})\)

44) \(\displaystyle (3,−\frac{π}{6},3)\)

For the following exercises, the spherical coordinates of a point are given. Find its associated cylindrical coordinates.

45) \(\displaystyle (2,−\frac{π}{4},\frac{π}{2})\)

Solution: \(\displaystyle (2,−\frac{π}{4},0)\)

46) \(\displaystyle (4,\frac{π}{4},\frac{π}{6})\)

47) \(\displaystyle (8,\frac{π}{3},\frac{π}{2})\)

Solution: \(\displaystyle (8,\frac{π}{3},0)\)

48) \(\displaystyle (9,−\frac{π}{6},\frac{π}{3})\)

For the following exercises, find the most suitable system of coordinates to describe the solids.

49) The solid situated in the first octant with a vertex at the origin and enclosed by a cube of edge length \(\displaystyle a\), where \(\displaystyle a>0\)

Solution: Cartesian system, \(\displaystyle {(x,y,z)|0≤x≤a,0≤y≤a,0≤z≤a}\)

50) A spherical shell determined by the region between two concentric spheres centered at the origin, of radii of \(\displaystyle a\) and \(\displaystyle b\), respectively, where \(\displaystyle b>a>0\)

51) A solid inside sphere \(\displaystyle x^2+y^2+z^2=9\) and outside cylinder \(\displaystyle (x−\frac{3}{2})^2+y^2=\frac{9}{4}\)

Solution: Cylindrical system, \(\displaystyle {(r,θ,z)∣r^2+z^2≤9,r≥3cosθ,0≤θ≤2π}\)

52) A cylindrical shell of height \(\displaystyle 10\) determined by the region between two cylinders with the same center, parallel rulings, and radii of \(\displaystyle 2\) and \(\displaystyle 5\), respectively

53) [T] Use a CAS to graph in cylindrical coordinates the region between elliptic paraboloid \(\displaystyle z=x^2+y^2\) and cone \(\displaystyle x^2+y^2−z^2=0.\)

Solution: The region is described by the set of points \(\displaystyle {(r,θ,z)∣∣0≤r≤1,0≤θ≤2π,r^2≤z≤r}.\)

54) [T] Use a CAS to graph in spherical coordinates the “ice cream-cone region” situated above the xy-plane between sphere \(\displaystyle x^2+y^2+z^2=4\) and elliptical cone \(\displaystyle x^2+y^2−z^2=0.\)

55) Washington, DC, is located at \(\displaystyle 39°\) N and \(\displaystyle 77°\) W (see the following figure). Assume the radius of Earth is \(\displaystyle 4000\) mi. Express the location of Washington, DC, in spherical coordinates.

Solution: \(\displaystyle (4000,−77°,51°)\)

56) San Francisco is located at \(\displaystyle 37.78°N\) and \(\displaystyle 122.42°W.\) Assume the radius of Earth is \(\displaystyle 4000\)mi. Express the location of San Francisco in spherical coordinates.

57) Find the latitude and longitude of Rio de Janeiro if its spherical coordinates are \(\displaystyle (4000,−43.17°,102.91°).\)

Solution: \(\displaystyle 43.17°W, 22.91°S\)

58) Find the latitude and longitude of Berlin if its spherical coordinates are \(\displaystyle (4000,13.38°,37.48°).\)

59) [T] Consider the torus of equation \(\displaystyle (x^2+y^2+z^2+R^2−r^2)^2=4R^2(x^2+y^2),\) where \(\displaystyle R≥r>0.\)

a. Write the equation of the torus in spherical coordinates.

b. If \(\displaystyle R=r,\) the surface is called a horn torus. Show that the equation of a horn torus in spherical coordinates is \(\displaystyle ρ=2Rsinφ.\)

c. Use a CAS to graph the horn torus with \(\displaystyle R=r=2\) in spherical coordinates.

Solution: \(\displaystyle a. ρ=0, ρ+R2−r2−2Rsinφ=0;\)

c.

60) [T] The “bumpy sphere” with an equation in spherical coordinates is \(\displaystyle ρ=a+bcos(mθ)sin(nφ)\), with \(\displaystyle θ∈[0,2π]\) and \(\displaystyle φ∈[0,π]\), where \(\displaystyle a\) and \(\displaystyle b\) are positive numbers and \(\displaystyle m\) and \(\displaystyle n\) are positive integers, may be used in applied mathematics to model tumor growth.

a. Show that the “bumpy sphere” is contained inside a sphere of equation \(\displaystyle ρ=a+b.\) Find the values of \(\displaystyle θ\) and \(\displaystyle φ\) at which the two surfaces intersect.

b. Use a CAS to graph the surface for \(\displaystyle a=14, b=2, m=4,\) and \(\displaystyle n=6\) along with sphere \(\displaystyle ρ=a+b.\)

c. Find the equation of the intersection curve of the surface at b. with the cone \(\displaystyle φ=\frac{π}{12}\). Graph the intersection curve in the plane of intersection.

Chapter Review Exercise

For the following exercises, determine whether the statement is true or false. Justify the answer with a proof or a counterexample.

1) For vectors \(\displaystyle a\) and \(\displaystyle b\) and any given scalar \(\displaystyle c, c(a⋅b)=(ca)⋅b.\)

Solution: True

2) For vectors \(\displaystyle a\) and \(\displaystyle b\) and any given scalar \(\displaystyle c, c(a×b)=(ca)×b\).

3) The symmetric equation for the line of intersection between two planes \(\displaystyle x+y+z=2\) and \(\displaystyle x+2y−4z=5\) is given by \(\displaystyle −\frac{x−1}{6}=\frac{y−1}{5}=z.\)

Solution: False

4) If \(\displaystyle a⋅b=0,\) then \(\displaystyle a\) is perpendicular to \(\displaystyle b\).

For the following exercises, use the given vectors to find the quantities.

5) \(\displaystyle a=9i−2j,b=−3i+j\)

a. \(\displaystyle 3a+b\)

b. \(\displaystyle |a|\)

c. \(\displaystyle a×|b×|a\)

d. \(\displaystyle b×|a\)

Solution: a. \(\displaystyle ⟨24,−5⟩;\) b. \(\displaystyle \sqrt{85}\); c. Can’t dot a vector with a scalar; d. \(\displaystyle −29\)

6) \(\displaystyle a=2i+j−9k,b=−i+2k,c=4i−2j+k\)

a. \(\displaystyle 2a−b\)

b. \(\displaystyle |b×c|\)

c. \(\displaystyle b×|b×c|\)

d. \(\displaystyle c×|b×a|\)

e. \(\displaystyle proj_ab\)

7) Find the values of \(\displaystyle a\) such that vectors \(\displaystyle ⟨2,4,a⟩\) and \(\displaystyle ⟨0,−1,a⟩\) are orthogonal.

Solution: \(\displaystyle a=±2\)

For the following exercises, find the unit vectors.

8) Find the unit vector that has the same direction as vector \(\displaystyle v\) that begins at \(\displaystyle (0,−3)\) and ends at \(\displaystyle (4,10).\)

9) Find the unit vector that has the same direction as vector \(\displaystyle v\) that begins at \(\displaystyle (1,4,10)\) and ends at \(\displaystyle (3,0,4).\)

Solution: \(\displaystyle ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩\)

For the following exercises, find the area or volume of the given shapes.

10) The parallelogram spanned by vectors \(\displaystyle a=⟨1,13⟩\) and \(\displaystyle b=⟨3,21⟩\)

11) The parallelepiped formed by \(\displaystyle a=⟨1,4,1⟩\) and \(\displaystyle b=⟨3,6,2⟩,\) and \(\displaystyle c=⟨−2,1,−5⟩\)

Solution: \(\displaystyle 27\)

For the following exercises, find the vector and parametric equations of the line with the given properties.

12) The line that passes through point \(\displaystyle (2,−3,7)\) that is parallel to vector \(\displaystyle ⟨1,3,−2⟩\)

13) The line that passes through points \(\displaystyle (1,3,5)\) and \(\displaystyle (−2,6,−3)\)

Solution: \(\displaystyle x=1−3t,y=3+3t,z=5−8t,r(t)=(1−3t)i+3(1+t)j+(5−8t)k\)

For the following exercises, find the equation of the plane with the given properties.

14) The plane that passes through point \(\displaystyle (4,7,−1)\) and has normal vector \(\displaystyle n=⟨3,4,2⟩\)

15) The plane that passes through points \(\displaystyle (0,1,5),(2,−1,6),\) and \(\displaystyle (3,2,5).\)

Solution: \(\displaystyle −x+3y+8z=43\)

For the following exercises, find the traces for the surfaces in planes \(\displaystyle x=k,y=k\), and \(\displaystyle z=k.\) Then, describe and draw the surfaces.

16) \(\displaystyle 9x^2+4y^2−16y+36z^2=20\)

17) \(\displaystyle x^2=y^2+z^2\)

Solution: \(\displaystyle x=k\) trace: \(\displaystyle k^2=y^2+z^2\) is a circle, \(\displaystyle y=k\) trace: \(\displaystyle x^2−z^2=k^2\) is a hyperbola (or a pair of lines if \(\displaystyle k=0), z=k\) trace: \(\displaystyle x^2−y^2=k^2\) is a hyperbola (or a pair of lines if \(\displaystyle k=0\)). The surface is a cone.

For the following exercises, write the given equation in cylindrical coordinates and spherical coordinates.

18) \(\displaystyle x^2+y^2+z^2=144\)

19) \(\displaystyle z=x^2+y^2−1\)

Solution: Cylindrical: \(\displaystyle z=r^2−1,\) spherical: \(\displaystyle cosφ=ρsin^2φ−\frac{1}{ρ}\)

For the following exercises, convert the given equations from cylindrical or spherical coordinates to rectangular coordinates. Identify the given surface.

20) \(\displaystyle ρ^2(sin^2(φ)−cos^2(φ))=1\)

21) \(\displaystyle r^2−2rcos(θ)+z^2=1\)

Solution: \(\displaystyle x^2−2x+y^2+z^2=1\), sphere

For the following exercises, consider a small boat crossing a river.

22) If the boat velocity is \(\displaystyle 5\)km/h due north in still water and the water has a current of \(\displaystyle 2\) km/h due west (see the following figure), what is the velocity of the boat relative to shore? What is the angle \(\displaystyle θ\) that the boat is actually traveling?

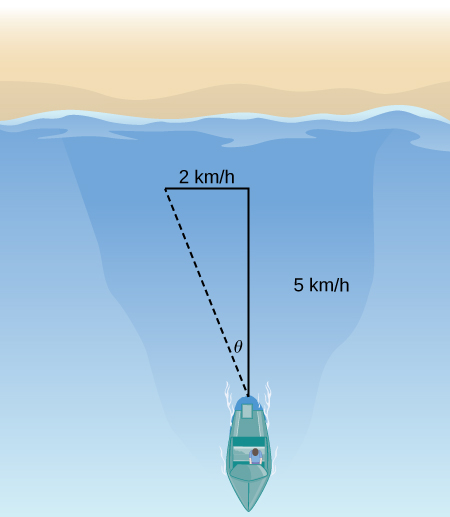
23) When the boat reaches the shore, two ropes are thrown to people to help pull the boat ashore. One rope is at an angle of \(\displaystyle 25°\) and the other is at \(\displaystyle 35°\). If the boat must be pulled straight and at a force of \(\displaystyle 500N\), find the magnitude of force for each rope (see the following figure).

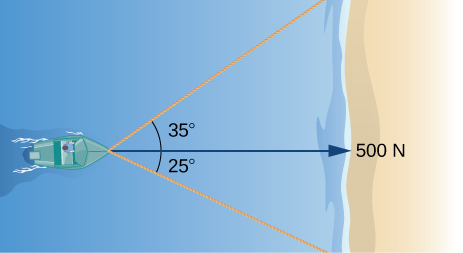
Solution: 331 N, and 244 N

24) An airplane is flying in the direction of 52° east of north with a speed of 450 mph. A strong wind has a bearing 33° east of north with a speed of 50 mph. What is the resultant ground speed and bearing of the airplane?

25) Calculate the work done by moving a particle from position \(\displaystyle (1,2,0)\) to \(\displaystyle (8,4,5)\) along a straight line with a force \(\displaystyle F=2i+3j−k.\)

Solution: \(\displaystyle 15J\)

The following problems consider your unsuccessful attempt to take the tire off your car using a wrench to loosen the bolts. Assume the wrench is \(\displaystyle 0.3\)m long and you are able to apply a 200-N force.

26) Because your tire is flat, you are only able to apply your force at a \(\displaystyle 60°\) angle. What is the torque at the center of the bolt? Assume this force is not enough to loosen the bolt.

27) Someone lends you a tire jack and you are now able to apply a 200-N force at an \(\displaystyle 80°\) angle. Is your resulting torque going to be more or less? What is the new resulting torque at the center of the bolt? Assume this force is not enough to loosen the bolt.

Solution: More, \(\displaystyle 59.09 J\)