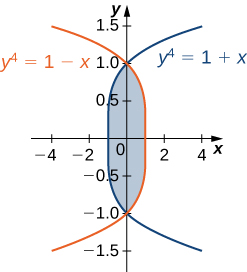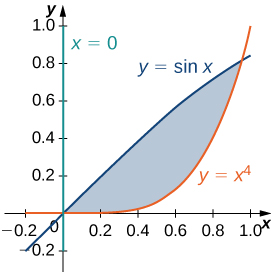15.E: Multiple Integration (Exercises)
- Page ID
- 5778
15.1: Double Integrals over Rectangular Regions
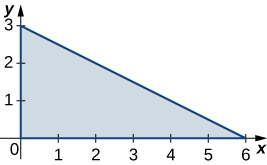
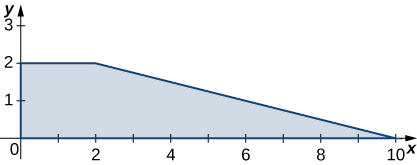
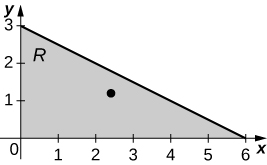
In the following exercises, use the midpoint rule with \(m = 4\) and \(n = 2\) to estimate the volume of the solid bounded by the surface \(z = f(x,y)\), the vertical planes \(x = 1\), \(x = 2\), \(y = 1\), and \(y = 2\), and the horizontal plane \(x = 0\).
\(f(x,y) = 4x + 2y + 8xy\)
[Hide Solution]
27.
\(f(x,y) = 16x^2 + \frac{y}{2}\)
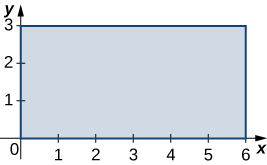
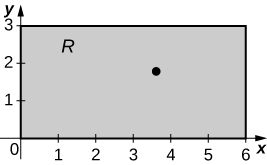
In the following exercises, estimate the volume of the solid under the surface \(z = f(x,y)\) and above the rectangular region R by using a Riemann sum with \(m = n = 2\) and the sample points to be the lower left corners of the subrectangles of the partition.
\(f(x,y) = sin \space x - cos \space y\), \(R = [0, \pi] \times [0, \pi]\)
[Hide Solution]
0.
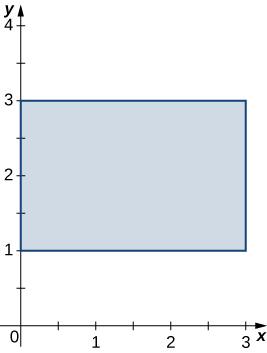
\(f(x,y) = cos \space x + cos \space y\), \(R = [0, \pi] \times [0, \frac{\pi}{2}]\)
Use the midpoint rule with \(m = n = 2\) to estimate \(\iint_R f(x,y) dA\), where the values of the function f on \(R = [8,10] \times [9,11]\) are given in the following table.
| y | |||||
|---|---|---|---|---|---|
| x | 9 | 9.5 | 10 | 10.5 | 11 |
| 8 | 9.8 | 5 | 6.7 | 5 | 5.6 |
| 8.5 | 9.4 | 4.5 | 8 | 5.4 | 3.4 |
| 9 | 8.7 | 4.6 | 6 | 5.5 | 3.4 |
| 9.5 | 6.7 | 6 | 4.5 | 5.4 | 6.7 |
| 10 | 6.8 | 6.4 | 5.5 | 5.7 | 6.8 |
[Hide Solution]
21.3.
The values of the function f on the rectangle \(R = [0,2] \times [7,9]\) are given in the following table. Estimate the double integral \(\iint_R f(x,y)dA\) by using a Riemann sum with \(m = n = 2\). Select the sample points to be the upper right corners of the subsquares of R.
| \(y_0 = 7\) | \(y_1 = 8\) | \(y_2 = 9\) | |
|---|---|---|---|
| \(x_0 = 0\) | 10.22 | 10.21 | 9.85 |
| \(x_1 = 1\) | 6.73 | 9.75 | 9.63 |
| \(x_2 = 2\) | 5.62 | 7.83 | 8.21 |
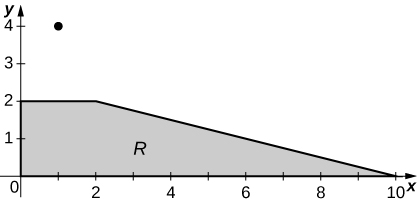
The depth of a children’s 4-ft by 4-ft swimming pool, measured at 1-ft intervals, is given in the following table.
- Estimate the volume of water in the swimming pool by using a Riemann sum with \(m = n = 2\). Select the sample points using the midpoint rule on \(R = [0,4] \times [0,4]\).
- Find the average depth of the swimming pool.
y x 0 1 2 3 4 0 1 1.5 2 2.5 3 1 1 1.5 2 2.5 3 2 1 1.5 1.5 2.5 3 3 1 1 1.5 2 2.5 4 1 1 1 1.5 2
[Hide Solution]
a. 28 \(ft^3\) b. 1.75 ft.
The depth of a 3-ft by 3-ft hole in the ground, measured at 1-ft intervals, is given in the following table.
- Estimate the volume of the hole by using a Riemann sum with \(m = n = 3\) and the sample points to be the upper left corners of the subsquares of \(R\).
- Find the average depth of the hole.
y x 0 1 2 3 0 6 6.5 6.4 6 1 6.5 7 7.5 6.5 2 6.5 6.7 6.5 6 3 6 6.5 5 5.6
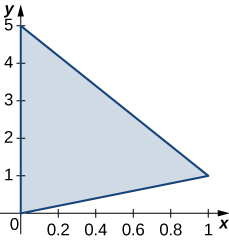
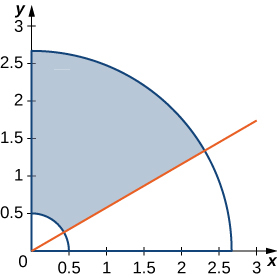
The level curves \(f(X,Y) = K\) of the function f are given in the following graph, where k is a constant.
- Apply the midpoint rule with \(M = N = 2\)m=n=2m=n=2 to estimate the double integral \(\iint_R f(x,y)dA\), where \(R = [0.2,1] \times [0,0.8]\).
- Estimate the average value of the function f on \(R\).
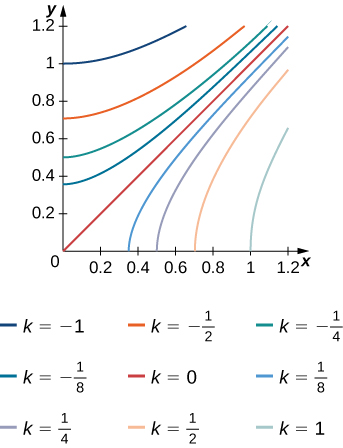
a. 0.112 b. \(f_{ave} ≃ 0.175\); here \(f(0.4,0.2) ≃ 0.1\), \(f(0.2,0.6) ≃− 0.2\), \(f(0.8,0.2) ≃ 0.6\), and \(f(0.8,0.6) ≃ 0.2\).
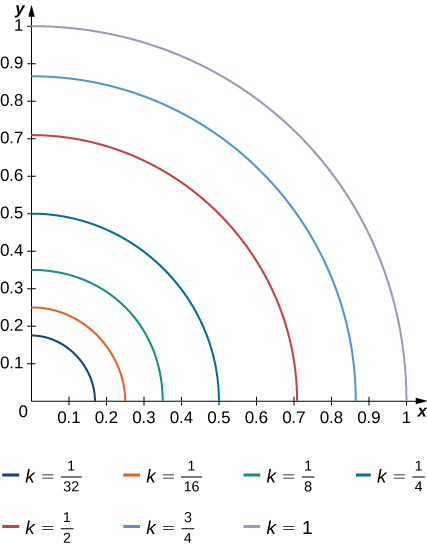
The level curves \(f(x,y) = k\) of the function f are given in the following graph, where k is a constant.
- Apply the midpoint rule with \(m = n = 2\) to estimate the double integral \(\iint_R f(x,y)dA\), where \(R = [0.1,0.5] \times [0.1,0.5]\).
- Estimate the average value of the function f on \(R\).
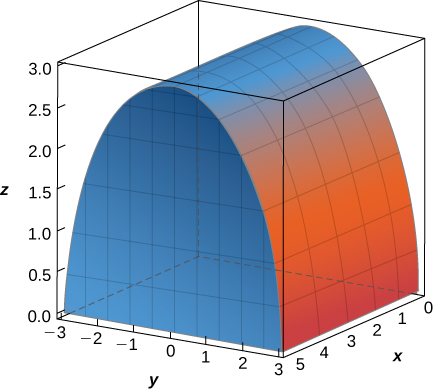
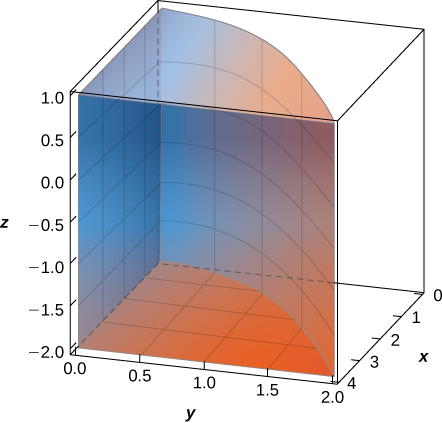
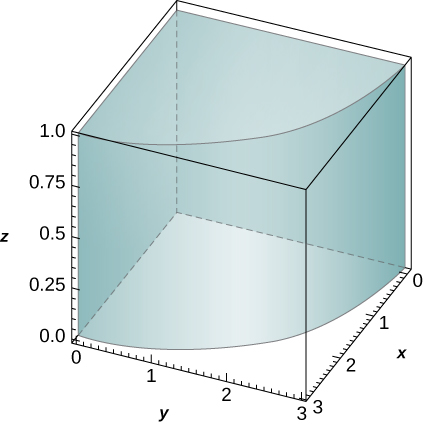
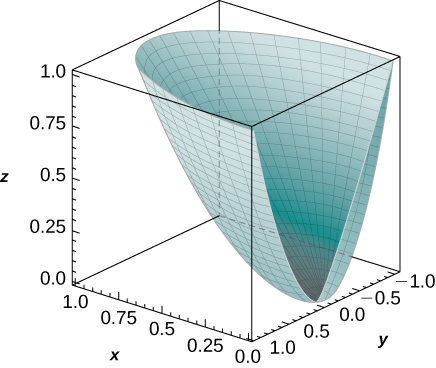
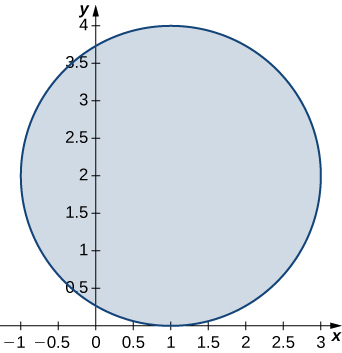
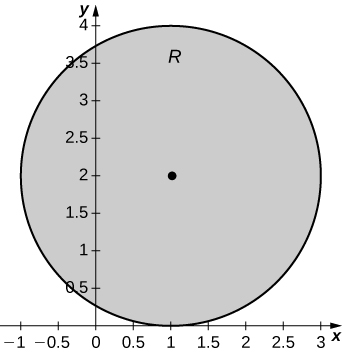
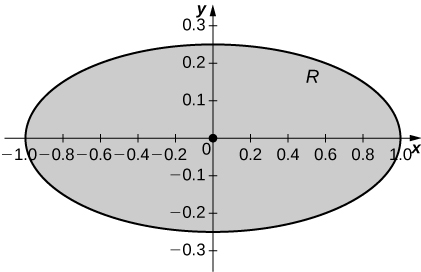
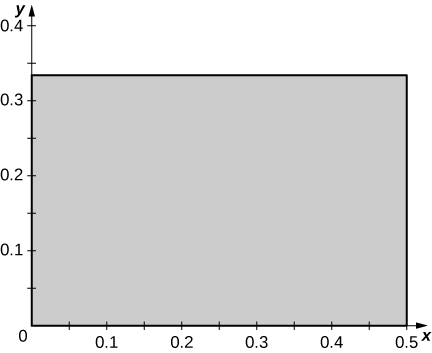
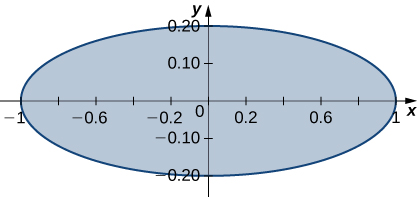
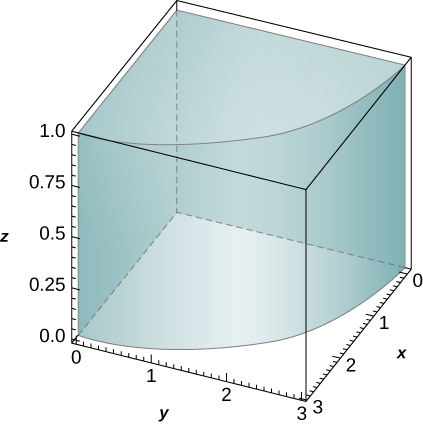
The solid lying under the surface \(z = \sqrt{4 - y^2}\) and above the rectangular region\( R = [0,2] \times [0,2]\) is illustrated in the following graph. Evaluate the double integral \(\iint_Rf(x,y)\), where \(f(x,y) = \sqrt{4 - y^2}\) by finding the volume of the corresponding solid.
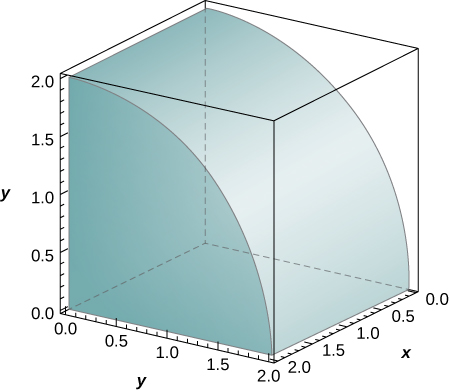
[Hide Solution]
\(2\pi\)
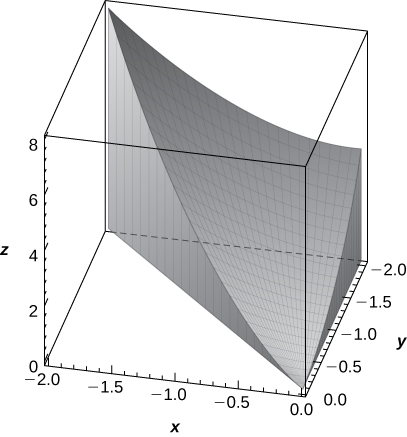
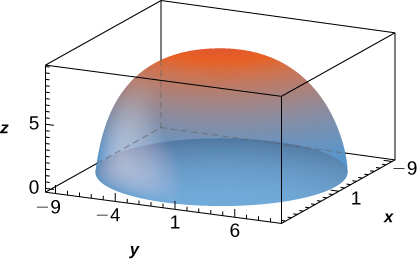
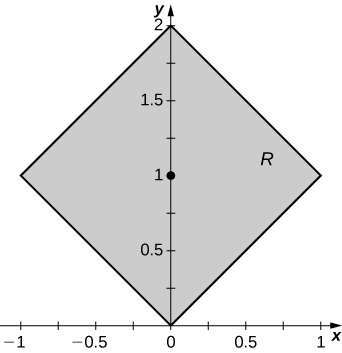
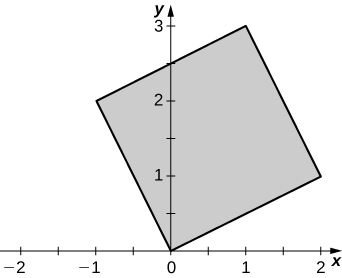
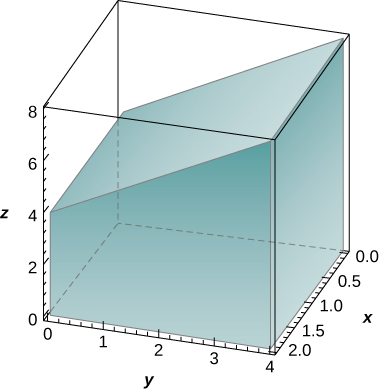
The solid lying under the plane \(z = y + 4\) and above the rectangular region \(R = [0,2] \times [0,4]\) is illustrated in the following graph. Evaluate the double integral \(\iint_R f(x,y)dA\), where \(f(x,y) = y + 4\), by finding the volume of the corresponding solid.
In the following exercises, calculate the integrals by interchanging the order of integration.
\[\int_{-1}^1\left(\int_{-2}^2 (2x + 3y + 5)dx \right) \space dy\]
[Hide Solution]
40.
\[\int_0^2\left(\int_0^1 (x + 2e^y + 3)dx \right) \space dy\]
\[\int_1^{27}\left(\int_1^2 (\sqrt[3]{x} + \sqrt[3]{y})dy \right) \space dx\]
[Hide Solution]
\(\frac{81}{2} + 39\sqrt[3]{2}\).
\[\int_1^{16}\left(\int_1^8 (\sqrt[4]{x} + 2\sqrt[3]{y})dy \right) \space dx\]
\[\int_{ln \space 2}^{ln \space 3}\left(\int_0^1 e^{x+y}dy \right) \space dx\]
[Hide Solution]
\(e - 1\).
\[\int_0^2\left(\int_0^1 3^{x+y}dy \right) \space dx\]
\[\int_1^6\left(\int_2^9 \frac{\sqrt{y}}{y^2}dy \right) \space dx\]
[Hide Solution]
\(15 - \frac{10\sqrt{2}}{9}\).
\[\int_1^9 \left(\int_4^2 \frac{\sqrt{x}}{y^2}dy \right) dx\]
In the following exercises, evaluate the iterated integrals by choosing the order of integration.
\[\int_0^{\pi} \int_0^{\pi/2} sin(2x)cos(3y)dx \space dy\]
[Hide Solution]
0.
\[\int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [cot \space x + tan(2y)]dx \space dy\]
\[\int_1^e \int_1^e \left[\frac{1}{x}sin(ln \space x) + \frac{1}{y}cos (ln \space y)\right] dx \space dy\]
[Hide Solution]
\((e − 1)(1 + sin1 − cos1)\)
\[\int_1^e \int_1^e \frac{sin(ln \space x)cos (ln \space y)}{xy} dx \space dy\]
\[\int_1^2 \int_1^2 \left(\frac{ln \space y}{x} + \frac{x}{2y + 1}\right) dy \space dx\]
[Hide solution]
\(\frac{3}{4}ln \left(\frac{5}{3}\right) + 2b \space ln^2 2 - ln \space 2\)
\[\int_1^e \int_1^2 x^2 ln(x) dy \space dx\]
\[\int_1^{\sqrt{3}} \int_1^2 y \space arctan \left(\frac{1}{x}\right) dy \space dx\]
[Hide Solution]
\(\frac{1}{8}[(2\sqrt{3} - 3) \pi + 6 \space ln \space 2]\).
\[\int_0^1 \int_0^{1/2} (arcsin \space x + arcsin \space y) dy \space dx\]
\[\int_0^1 \int_0^2 xe^{x+4y} dy \space dx\]
[Hide Solution]
\(\frac{1}{4}e^4 (e^4 - 1)\).
\[\int_1^2 \int_0^1 xe^{x-y} dy \space dx\]
\[\int_1^e \int_1^e \left(\frac{ln \space y}{\sqrt{y}} + \frac{ln \space x}{\sqrt{x}}\right) dy \space dx\]
[Hide Solution]
\(4(e - 1)(2 - \sqrt{e})\).
\[\int_1^e \int_1^e \left(\frac{x \space ln \space y}{\sqrt{y}} + \frac{y \space ln \space x}{\sqrt{x}}\right) dy \space dx\]
\[\int_0^1 \int_1^2 \left(\frac{x}{x^2 + y^2} \right) dy \space dx\]
[Hide Solution]
\(-\frac{\pi}{4} + ln \left(\frac{5}{4}\right) - \frac{1}{2} ln \space 2 + arctan \space 2\).
\[\int_0^1 \int_1^2 \frac{y}{x + y^2} dy \space dx\]
In the following exercises, find the average value of the function over the given rectangles.
\(f(x,y) = −x +2y\), \(R = [0,1] \times [0,1]\)
[Hide Solution]
\(\frac{1}{2}\).
\(f(x,y) = x^4 + 2y^3\), \(R = [1,2] \times [2,3]\)
\(f(x,y) = sinh \space x + sinh \space y\), \(R = [0,1] \times [0,2]\)
[Hide solution]
\(\frac{1}{2}(2 \space cosh \space 1 + cosh \space 2 - 3)\).
\(f(x,y) = arctan(xy)\), \(R = [0,1] \times [0,1]\)
Let f and g be two continuous functions such that \(0 \leq m_1 \leq f(x) \leq M_1\) for any \(x ∈ [a,b]\) and \(0 \leq m_2 \leq g(y) \leq M_2\) for any\( y ∈ [c,d]\). Show that the following inequality is true:
\[m_1m_2(b-a)(c-d) \leq \int_a^b \int_c^d f(x) g(y) dy dx \leq M_1M_2 (b-a)(c-d).\]
In the following exercises, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.
\(\frac{1}{e^2} \leq \iint_R e^{-x^2 - y^2} \space dA \leq 1\), where \(R = [0,1] \times [0,1]\)
\(\frac{\pi^2}{144} \leq \iint_R sin \space x \space cos y \space dA \leq \frac{\pi^2}{48}\), where \(R = \left[ \frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[ \frac{\pi}{6}, \frac{\pi}{3}\right]\)
\(0 \leq \iint_R e^{-y}\space cos x \space dA \leq \frac{\pi}{2}\), where \(R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]\)
\(0 \leq \iint_R (ln \space x)(ln \space y) dA \leq (e - 1)^2\), where \(R = [1, e] \times [1, e] \)
Let f and g be two continuous functions such that \(0 \leq m_1 \leq f(x) \leq M_1\) for any \(x ∈ [a,b]\) and \(0 \leq m_2 \leq g(y) \leq M_2\) for any \(y ∈ [c,d]\). Show that the following inequality is true:
\((m_1 + m_2) (b - a)(c - d) \leq \int_a^b \int_c^d |f(x) + g(y)| \space dy \space dx \leq (M_1 + M_2)(b - a)(c - d)\).
In the following exercises, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.
\(\frac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) dA \leq 2\), where \(R = [0,1] \times [0,1]\)
\(\frac{\pi^2}{36}\iint_R (sin \space x + cos \space y)dA \leq \frac{\pi^2 \sqrt{3}}{36}\), where \(R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]\)
\(\frac{\pi}{2}e^{-\pi/2} \leq \iint_R (cos \space x + e^{-y})dA \leq \pi\), where \(R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]\)
\(\frac{1}{e} \leq \iint_R (e^{-y} - ln \space x) dA \leq 2\), where \(R = [0, 1] \times [0, 1]\)
In the following exercises, the function f is given in terms of double integrals.
- Determine the explicit form of the function f.
- Find the volume of the solid under the surface \(z = f(x,y)\) and above the region R.
- Find the average value of the function f on R.
- Use a computer algebra system (CAS) to plot \(z = f(x,y)\) and \(z = f_{ave}\) in the same system of coordinates.
[T] \(f(x,y) = \int_0^y \int_0^x (xs + yt) ds \space dt\), where \((x,y) \in R = [0,1] \times [0,1]\)
[Hide Solution]
a. \(f(x,y) = \frac{1}{2} xy (x^2 + y^2)\); b. \(V = \int_0^1 \int_0^1 f(x,y) dx \space dy = \frac{1}{8}\); c. \(f_{ave} = \frac{1}{8}\);
d.
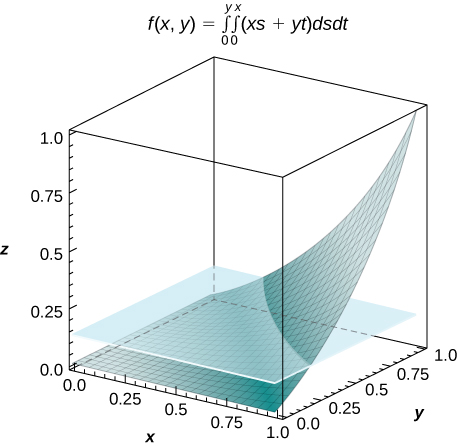
[T] \(f(x,y) = \int_0^x \int_0^y [cos \space (s) + cos \space (t)] dt \space ds\), where \((x,y) \in R = [0,3] \times [0,3]\)
Show that if f and g are continuous on \([a,b]\) and \([c,d]\), respectively, then
\(\int_a^b \int_c^d |f(x) + g(y)| dy \space dx = (d - c) \int_a^b f(x)dx\)
\(+ \int_a^b \int_c^d g(y)dy \space dx = (b - a) \int_c^d g(y)dy + \int_c^d \int_a^b f(x) dx \space dy\).
Show that \(\int_a^b \int_c^d yf(x) + xg(y) dy \space dx = \frac{1}{2} (d^2 - c^2) \left(\int_a^b f(x)dx\right) + \frac{1}{2} (b^2 - a^2) \left(\int_c^d g(y)dy\right)\).
[T] Consider the function \(f(x,y) = e^{-x^2-y^2}\), where \((x,y) \in R = [−1,1] \times [−1,1]\).
- Use the midpoint rule with \(m = n = 2,4,..., 10\) to estimate the double integral \(I = \iint_R e^{-x^2 - y^2} dA\). Round your answers to the nearest hundredths.
- For \(m = n = 2\), find the average value of f over the region R. Round your answer to the nearest hundredths.
- Use a CAS to graph in the same coordinate system the solid whose volume is given by \(\iint_R e^{-x^2-y^2} dA\) and the plane \(z = f_{ave}\).
[Hide Solution]
a. For \(m = n = 2\), \(I = 4e^{-0.5} \approx 2.43\) b. \(f_{ave} = e^{-0.5} \simeq 0.61\);
c.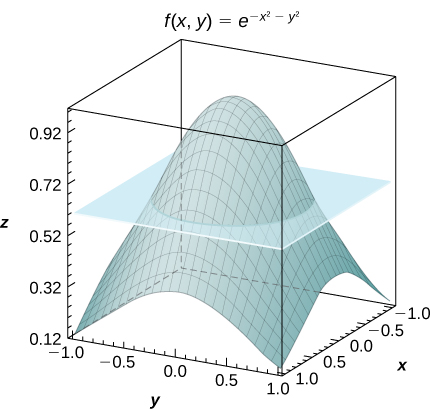
[T] Consider the function \(f(x,y) = sin \space (x^2) \space cos \space (y^2)\), where \((x,y \in R = [−1,1] \times [−1,1]\).
- Use the midpoint rule with \(m = n = 2,4,..., 10\) to estimate the double integral \(I = \iint_R sin \space (x^2) \space cos \space (y^2) \space dA\). Round your answers to the nearest hundredths.
- For \(m = n = 2\), find the average value of f over the region R. Round your answer to the nearest hundredths.
- Use a CAS to graph in the same coordinate system the solid whose volume is given by \(\iint_R sin \space (x^2) \space cos \space (y^2) \space dA\) and the plane \(z = f_{ave}\).
In the following exercises, the functions fnfn are given, where \(n \geq 1\) is a natural number.
- Find the volume of the solids \(S_n\) under the surfaces \(z = f_n(x,y)\) and above the region R.
- Determine the limit of the volumes of the solids \(S_n\) as n increases without bound.
\(f(x,y) = x^n + y^n + xy, \space (x,y) \in R = [0,1] \times [0,1]\)
[Hide Solution]
a. \(\frac{2}{n + 1} + \frac{1}{4}\) b. \(\frac{1}{4}\)
\(f(x,y) = \frac{1}{x^n} + \frac{1}{y^n}, \space (x,y) \in R = [1,2] \times [1,2]\)
Show that the average value of a function f on a rectangular region \(R = [a,b] \times [c,d]\) is \(f_{ave} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\),where \((x_{ij}^*,y_{ij}^*)\) are the sample points of the partition of R, where \(1 \leq i \leq m\) and \(1 \leq j \leq n\).
Use the midpoint rule with \(m = n\) to show that the average value of a function f on a rectangular region \(R = [a,b] \times [c,d]\) is approximated by
\[f_{ave} \approx \frac{1}{n^2} \sum_{i,j =1}^n f \left(\frac{1}{2} (x_{i=1} + x_i), \space \frac{1}{2} (y_{j=1} + y_j)\right).\]
An isotherm map is a chart connecting points having the same temperature at a given time for a given period of time. Use the preceding exercise and apply the midpoint rule with \(m = n = 2\) to find the average temperature over the region given in the following figure.
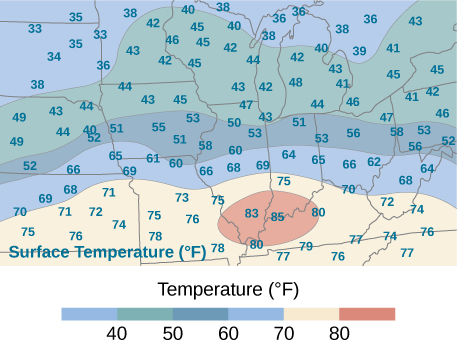
[Hide Solution]
\(56.5^{\circ}\) F; here \(f(x_1^*,y_1^*) = 71, \space f(x_2^*, y_1^*) = 72, \space f(x_2^*,y_1^*) = 40, \space f(x_2^*,y_2^*) = 43\), where \(x_i^*\) and \(y_j^*\) are the midpoints of the subintervals of the partitions of [a,b] and [c,d], respectively
15.2: Double Integrals over General Regions
In the following exercises, specify whether the region is of Type I or Type II.
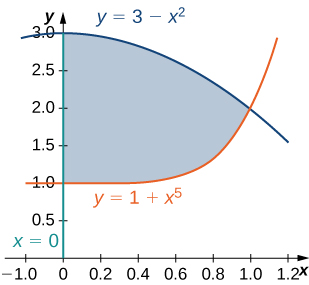
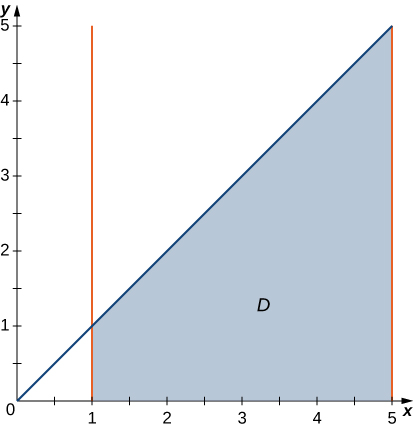
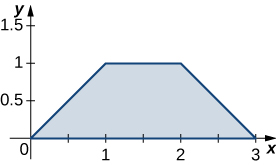
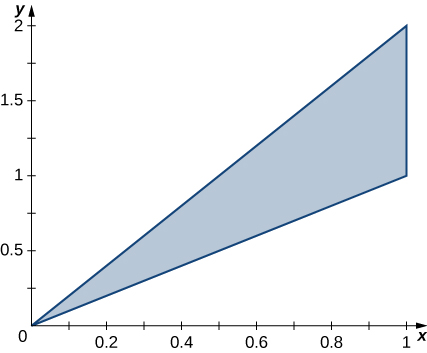
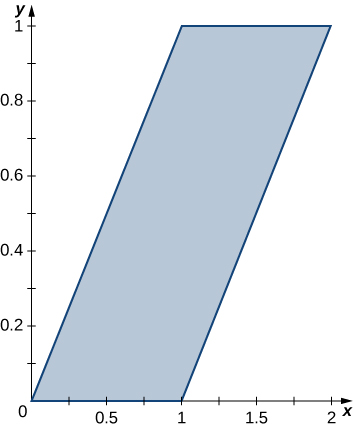
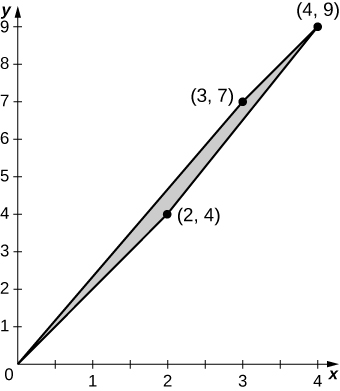
The region \(D\) bounded by \(y = x^3, \space y = x^3 + 1, \space x = 0,\) and \(x = 1\) as given in the following figure.
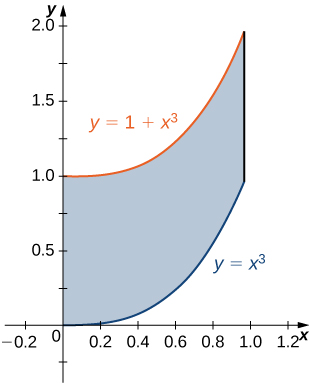
Find the average value of the function \(f(x,y) = 3xy\) on the region graphed in the previous exercise.
[Hide Solution]
\(\frac{27}{20}\)
Find the area of the region \(D\) given in the previous exercise.
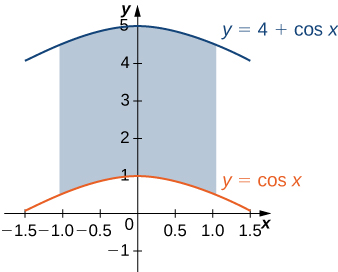
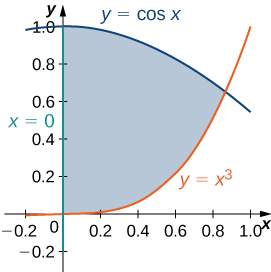
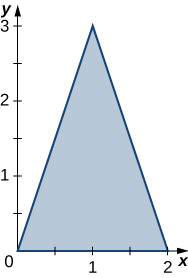
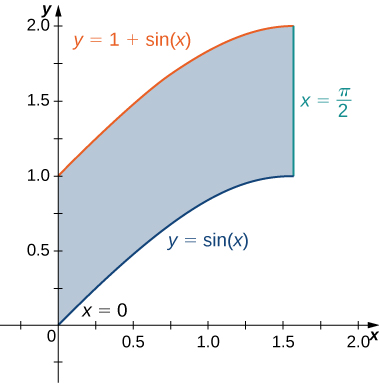
The region \(D\) bounded by \(y = sin \space x, \space y = 1 + sin \space x, \space x = 0\), and \(x = \frac{\pi}{2}\) as given in the following figure.
[Hide Solution]
Type I but not Type II
Find the average value of the function \(f(x,y) = cos \space x\) on the region graphed in the previous exercise.
Find the area of the region \(D\) given in the previous exercise.
[Hide Solution]
\(\frac{\pi}{2}\)
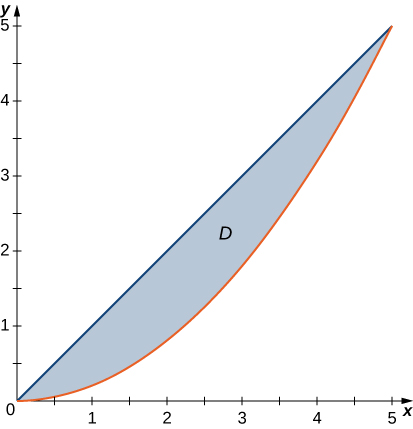
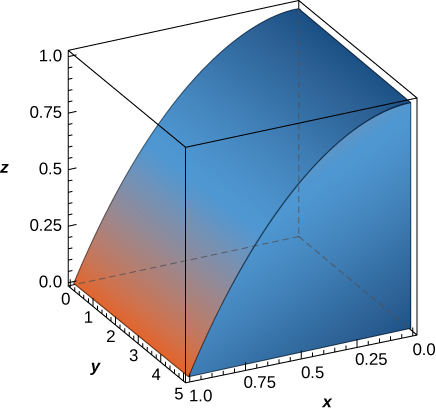
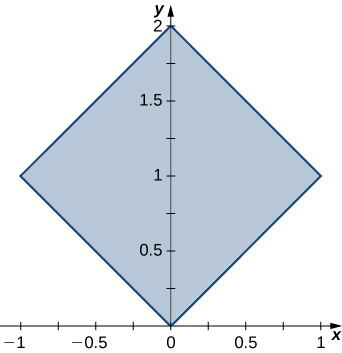
The region \(D\) bounded by \(x = y^2 - 1\) and \(x = \sqrt{1 - y^2}\) as given in the following figure.
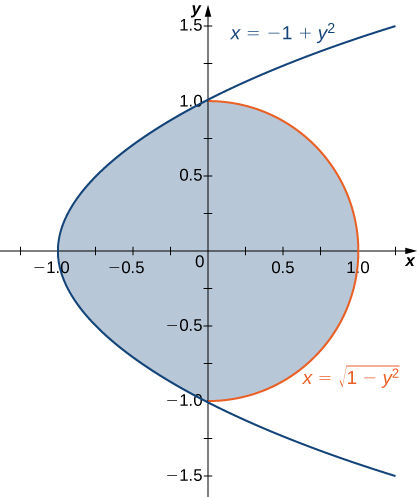
Find the volume of the solid under the graph of the function \(f(x,y) = xy + 1\) and above the region in the figure in the previous exercise.
[Hide Solution]
\(\frac{1}{6}(8 + 3\pi)\)
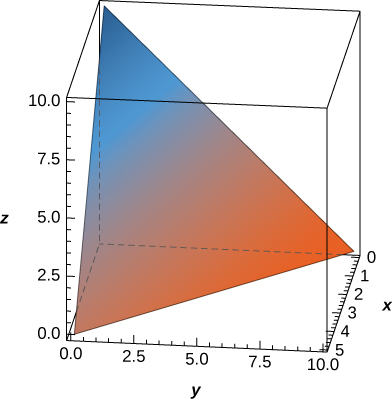
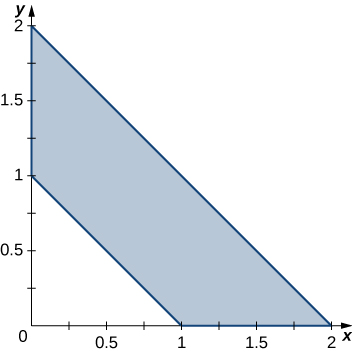
The region \(D\) bounded by \(y = 0, \space x = -10 + y,\) and \(x = 10 - y\) as given in the following figure.
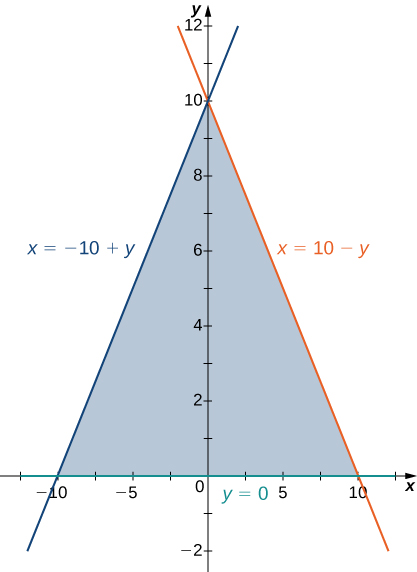
Find the volume of the solid under the graph of the function \(f(x,y) = x + y\) and above the region in the figure from the previous exercise.
[Hide Solution]
\(\frac{1000}{3}\)
The region \(D\) bounded by \(y = 0, \space x = y - 1, \space x = \frac{\pi}{2}\) as given in the following figure.

The region \(D\) bounded by \(y = 0\) and \(y = x^2 - 1\) as given in the following figure.
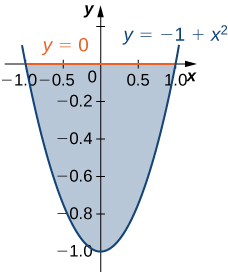
Type I and Type II
Let \(D\) be the region bounded by the curves of equations \(y = x, \space y = -x\) and \(y = 2 - x^2\). Explain why \(D\) is neither of Type I nor II.
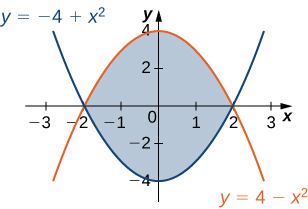
Let \(D\) be the region bounded by the curves of equations \(y = cos \space x\) and \(y = 4 - x^2\) and the \(x\)-axis. Explain why \(D\) is neither of Type I nor II.
[Hide Solution]
The region \(D\) is not of Type I: it does not lie between two vertical lines and the graphs of two continuous functions \(g_1(x)\) and \(g_2(x)\). The region