1.E: Right Triangle Trigonometry Angles (Exercises)
- Page ID
- 3398
These are homework exercises to accompany Corral's "Elementary Trigonometry" Textmap. This is a text on elementary trigonometry, designed for students who have completed courses in high-school algebra and geometry. Though designed for college students, it could also be used in high schools. The traditional topics are covered, but a more geometrical approach is taken than usual. Also, some numerical methods (e.g. the secant method for solving trigonometric equations) are discussed.
1.1 Exercises
For Exercises 1-4, find the numeric value of the indicated angle(s) for the triangle \(\triangle\,ABC \).
1.1.1 Find \(B \) if \(A = 15^\circ \) and \(C = 50^\circ \).
1.1.2 Find \(C \) if \(A = 110^\circ \) and \(B = 31^\circ \).
1.1.3 Find \(A \) and \(B \) if \(C = 24^\circ \), \(A = \alpha \), and \(B = 2\alpha \).
1.1.4 Find \(A \), \(B \), and \(C \) if \(A = \beta \) and \(B = C = 4\beta \).
For Exercises 5-8, find the numeric value of the indicated angle(s) for the right triangle \(\triangle\,ABC \), with \(C \) being the right angle.
1.1.5 Find \(B \) if \(A = 45^\circ \).
1.1.6 Find \(A \) and \(B \) if \(A = \alpha \) and \(B = 2\alpha \).
1.1.7 Find \(A \) and \(B \) if \(A = \phi \) and \(B = \phi^2 \).
1.1.8 Find \(A \) and \(B \) if \(A = \theta \) and \(B = 1/\theta \).
1.1.9 A car goes 24 miles due north then 7 miles due east. What is the straight distance between the car's starting point and end point?
1.1.10 One end of a rope is attached to the top of a pole 100 ft high. If the rope is 150 ft long, what is the maximum distance along the ground from the base of the pole to where the other end can be attached? You may assume that the pole is perpendicular to the ground.
1.1.11 Prove that the hypotenuse is the longest side in every right triangle. (Hint: Is \(a^2 + b^2 > a^2\)?)
1.1.12 Can a right triangle have sides with lengths 2, 5, and 6? Explain your answer.
1.1.13 If the lengths \(a \), \(b \), and \(c \) of the sides of a right triangle are positive integers, with \(a^2 + b^2 = c^2 \), then they form what is called a Pythagorean triple. The triple is normally written as (\(a \),\(b \),\(c\)). For example, (3,4,5) and (5,12,13) are well-known Pythagorean triples.
(a) Show that (6,8,10) is a Pythagorean triple.
(b) Show that if (\(a \),\(b \),\(c\)) is a Pythagorean triple then so is (\(ka \),\(kb \),\(kc\)) for any integer \(k >0 \). How would you interpret this geometrically?
(c) Show that (\(2mn \),\(m^2 - n^2 \),\(m^2 + n^2\)) is a Pythagorean triple for all integers \(m > n > 0 \).
(d) The triple in part(c) is known as Euclid's formula for generating Pythagorean triples. Write down the first ten Pythagorean triples generated by this formula, i.e. use: \(m=2 \) and \(n=1\); \(m=3 \) and \(n=1 \), \(2\); \(m=4 \) and \(n=1 \), \(2 \), \(3\); \(m=5 \) and \(n=1 \), \(2 \), \(3 \), \(4 \).
1.1.14 This exercise will describe how to draw a line through any point outside a circle such that the line intersects the circle at only one point. This is called a tangent line to the circle (see the picture on the left in Figure 1.1.6), a notion which we will use throughout the text.
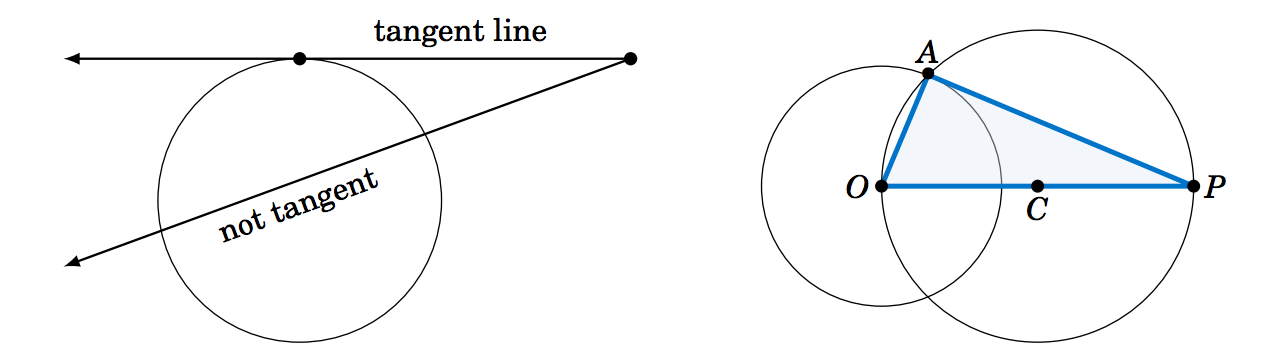
Figure 1.1.6
On a sheet of paper draw a circle of radius 1 inch, and call the center of that circle \(O \). Pick a point \(P \) which is \(2.5 \) inches away from \(O \). Draw the circle which has \(\overline{OP} \) as a diameter, as in the picture on the right in Figure 1.1.6. Let \(A \) be one of the points where this circle intersects the first circle. Draw the line through \(P \) and \(A \). In general the tangent line through a point on a circle is perpendicular to the line joining that point to the center of the circle (why?). Use this fact to explain why the line you drew is the tangent line through \(A \) and to calculate the length of \(\overline{PA} \). Does it match the physical measurement of \(\overline{PA}\)?
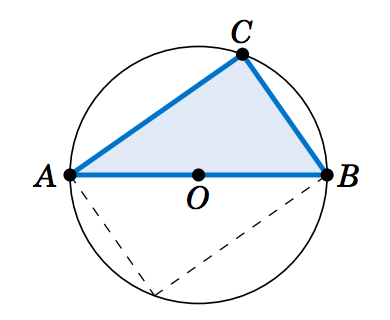
1.1.15 Suppose that \(\triangle\,ABC \) is a triangle with side \(\overline{AB} \) a diameter of a circle with center \(O \), as in the picture on the right, and suppose that the vertex \(C \) lies on the circle. Now imagine that you rotate the circle \(180^\circ \) around its center, so that \(\triangle\,ABC \) is in a new position, as indicated by the dashed lines in the picture. Explain how this picture proves Thales' Theorem.
1.2 Exercises
For Exercises 1-10, find the values of all six trigonometric functions of\\angles \(A\) and \(B \) in the right triangle \(\triangle\,ABC \) in Figure 1.2.3.
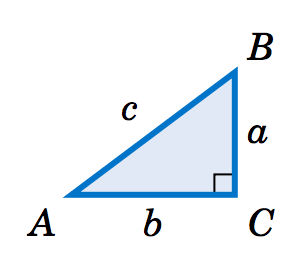
Figure 1.2.3
1.2.1 \(a = 5 \), \(b = 12 \), \(c = 13\)
1.2.2 \(a = 8 \), \(b = 15 \), \(c = 17\)
1.2.3 \(a = 7 \), \(b = 24 \), \(c = 25\)
1.2.4 \(a = 20 \), \(b = 21 \), \(c = 29\)
1.2.5 \(a = 9 \), \(b = 40 \), \(c = 41\)
1.2.6 \(a = 1 \), \(b = 2 \), \(c = \sqrt{5}\)
1.2.7 \(a = 1 \), \(b = 3\)
1.2.8 \(a = 2 \), \(b = 5\)
1.2.9 \(a = 5 \), \(c = 6\)
1.2.10 \(b = 7 \), \(c = 8\)
For Exercises 11-18, find the values of the other five trigonometric functions of the acute angle \(A \) given the indicated value of one of the functions.
1.2.11 \(\sin\;A = \frac{3}{4}\)
1.2.12 \(\cos\;A = \frac{2}{3}\)
1.2.13 \(\cos\;A = \frac{2}{\sqrt{10}}\)
1.2.14 \(\sin\;A = \frac{2}{4}\)
1.2.15 \(\tan\;A = \frac{5}{9}\)
1.2.16 \(\tan\;A = 3\)
1.2.17 \(\sec\;A = \frac{7}{3}\)
1.2.18 \(\csc\;A = 3\)
For Exercises 19-23, write the given number as a trigonometric function of an acute angle less than \(45^\circ \).
1.2.19 \(\sin\;87^\circ\)
1.2.20 \(\sin\;53^\circ\)
1.2.21 \(\cos\;46^\circ\)
1.2.22 \(\tan\;66^\circ\)
1.2.23 \(\sec\;77^\circ\)
For Exercises 24-28, write the given number as a trigonometric function of an acute angle greater than \(45^\circ \).
1.2.24 \(\sin\;1^\circ\)
1.2.25 \(\cos\;13^\circ\)
1.2.26 \(\tan\;26^\circ\)
1.2.27 \(\cot\;10^\circ\)
1.2.28 \(\csc\;43^\circ\)
1.2.29 In Example 1.7 we found the values of all six trigonometric functions of \(60^\circ \) and \(30^\circ \).
(a) Does \(\;\sin\;30^\circ ~+~ \sin\;30^\circ ~=~ \sin\;60^\circ\)?
(b) Does \(\;\cos\;30^\circ ~+~ \cos\;30^\circ ~=~ \cos\;60^\circ\)?
(c) Does \(\;\tan\;30^\circ ~+~ \tan\;30^\circ ~=~ \tan\;60^\circ\)?
(d) Does \(\;2\,\sin\;30^\circ\,\cos\;30^\circ ~=~ \sin\;60^\circ\)?
1.2.30 For an acute angle \(A \), can \(\sin\;A \) be larger than \(1\)? Explain your answer.
1.2.31 For an acute angle \(A \), can \(\cos\;A \) be larger than \(1\)? Explain your answer.
1.2.32 For an acute angle \(A \), can \(\sin\;A \) be larger than \(\tan\;A\)? Explain your answer.
1.2.33 If \(A \) and \(B \) are acute angles and \(A < B \), explain why \(\sin\;A < \sin\;B \).
1.2.34 If \(A \) and \(B \) are acute angles and \(A < B \), explain why \(\cos\;A > \cos\;B \).
1.2.35 Prove the Cofunction Theorem (Theorem 1.2). (Hint: Draw a right triangle and label the angles and sides.)
1.2.36 Use Example 1.10 to find all six trigonometric functions of \(15^\circ \).
1.2.37 In Figure 1.2.4, \(\overline{CB} \) is a diameter of a circle with a radius of \(2 \) cm and center \(O \), \(\triangle\,ABC \) is a right triangle, and \(\overline{CD}\) has length \(\sqrt{3} \) cm.
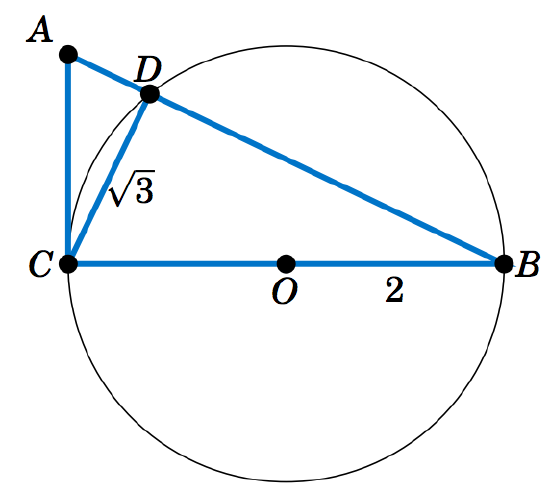
Figure 1.2.4
(a) Find \(\;\sin\;A \). (Hint: Use Thales' Theorem.)
(b) Find the length of \(\;\overline{AC} \).
(c) Find the length of \(\;\overline{AD} \).
(d) Figure 1.2.4 is drawn to scale. Use a protractor to measure the angle \(A \), then use your calculator to find\\the sine of that angle. Is the calculator result close to your answer from part(a)? Note: Make sure that your calculator is in degree mode.
1.2.38 In Exercise 37, verify that the area of \(\triangle\,ABC \) equals \(\frac{1}{2} AB \cdot CD \). Why does this make sense?
1.2.39 In Exercise 37, verify that the area of \(\triangle\,ABC \) equals \(\frac{1}{2} AB \cdot AC \; \sin\;A \).
1.2.40 In Exercise 37, verify that the area of \(\triangle\,ABC \) equals \(\frac{1}{2} (BC)^2 \;\cot\;A \).
1.3 Exercises
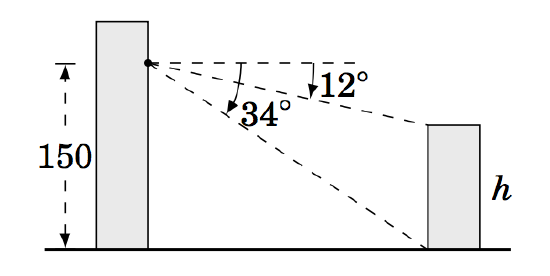
1.3.1 From a position \(150 \) ft above the ground, an observer in a building measures angles of depression of \(12^\circ \) and \(34^\circ \) to the top and bottom, respectively, of a smaller building, as in the picture on the right. Use this to find the height \(h \) of the smaller building.
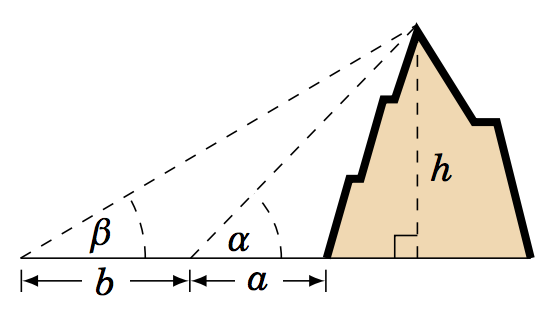
1.3.2 Generalize Example 1.12: A person standing \(a \) ft from the base of a mountain measures an angle of elevation \(\alpha \) from the ground to the top of the mountain. The person then walks \(b \) ft straight back and measures an angle of elevation \(\beta \) to the top of the mountain, as in the picture on the right. Assuming the ground is level, find a formula for the height \(h \) of the mountain in terms of \(a \), \(b \), \(\alpha \), and \(\beta \).
1.3.3 As the angle of elevation from the top of a tower to the sun decreases from \(64^\circ \) to \(49^\circ \) during the day, the length of the shadow of the tower increases by \(92 \) ft along the ground. Assuming the ground is level, find the height of the tower.
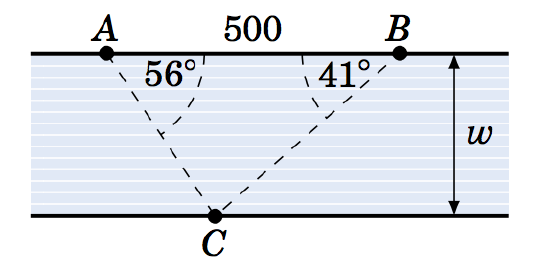
1.3.4 Two banks of a river are parallel, and the distance between two points \(A \) and \(B \) along one bank is \(500 \) ft. For a point \(C \) on the opposite bank, \(\angle\,BAC = 56^\circ \) and \(\angle\,ABC = 41^\circ \), as in the picture on the right. What is the width \(w \) of the river? (Hint: Divide \(\overline{AB} \) into two pieces.)
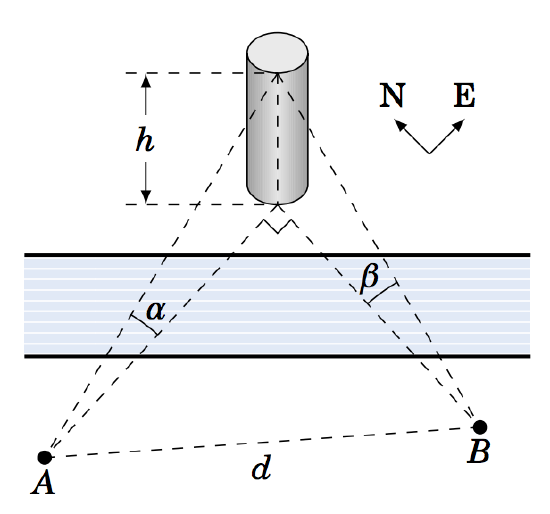
1.3.5 A tower on one side of a river is directly east and north of points \(A \) and \(B \), respectively, on the other side of the river. The top of the tower has angles of elevation \(\alpha\) and \(\beta \) from \(A \) and \(B \), respectively, as in the picture on the right. Let \(d \) be the distance between \(A \) and \(B \). Assuming that both sides of the river are at the same elevation, show that the height \(h \) of the tower is
\[\nonumber
h ~=~ \frac{d}{\sqrt{(\cot\,\alpha)^2 ~+~ (\cot\,\beta)^2}} ~.
\]
1.3.6 The equatorial parallax of the moon has been observed to be approximately \(57' \). Taking the radius of the earth to be \(3956.6 \) miles, estimate the distance from the center of
the earth to the moon. (Hint: See Example 1.15.)
1.3.7 An observer on earth measures an angle of \(31'\;7'' \) from one visible edge of the moon to the other (opposite) edge. Use this to estimate the radius of the moon. (Hint: Use Exercise
6 and see Example 1.16.)
1.3.8 A ball bearing sits between two metal grooves, with the top groove having an angle of \(120^\circ \) and the bottom groove having an angle of \(90^\circ \), as in the picture on the right. What must the diameter of the ball bearing be for the distance between the vertexes of the grooves to be half an inch? You may assume that the top vertex is directly above the bottom vertex.
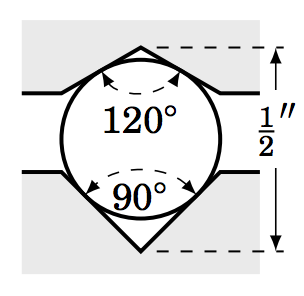
1.3.9 The machine tool diagram on the right shows a symmetric worm thread, in which a circular roller of diameter \(1.5 \) inches sits. Find the amount \(d \) that the top of the roller rises above the top of the thread, given the information in the diagram. (Hint: Extend the slanted sides of the thread until they meet at a point.)
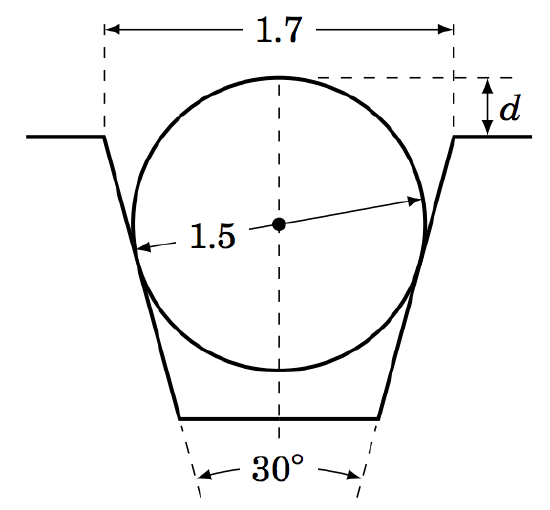
1.3.10 Repeat Exercise 9 using \(1.8 \) inches as the distance across the top of the worm thread.
1.3.11 In Exercise 9, what would the distance across the top of the worm thread have to be to make \(d \) equal to \(0 \) inches?
1.3.12 For \(0^\circ < \theta < 90^\circ \) in the slider-crank mechanism in Example 1.18, show that
\[\nonumber
c ~=~ \frac{\sqrt{b^2 ~-~ r^2 \;(\sin\,\theta)^2}}{\cos\;\theta} ~\qquad\text{and}\qquad~
a ~=~ r\;\sin\;\theta ~+~ \sqrt{b^2 ~-~ r^2 \;(\sin\,\theta)^2}~\tan\;\theta ~.
\]
(Hint: In Figure 1.3.2 draw line segments from \(B \) perpendicular to \(\overline{OA} \) and \(\overline{AC} \).)
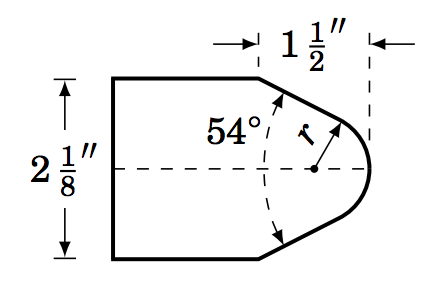
1.3.13 The machine tool diagram on the right shows a symmetric die punch. In this view, the rounded tip is part of a circle of radius \(r \), and the slanted sides are tangent to that circle and form an angle of \(54^\circ \). The top and bottom sides of the die punch are horizontal. Use the
information in the diagram to find the radius \(r \).
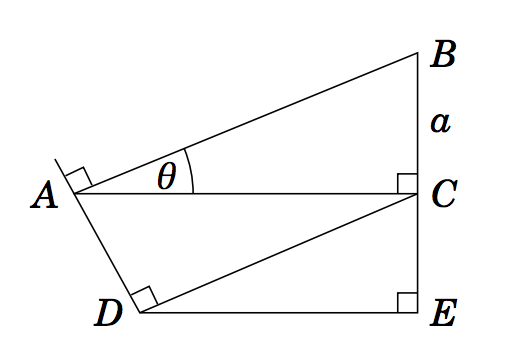
1.3.14 In the figure on the right, \(\angle\,BAC = \theta \) and \(BC = a \). Use this to find \(AB \), \(AC \), \(AD \), \(DC \), \(CE \), and \(DE \) in terms of \(\theta \) and \(a \).(Hint: What is the angle \(\angle\,ACD\,\)?)
For Exercises 15-23, solve the right triangle in Figure 1.3.4 using the given information.
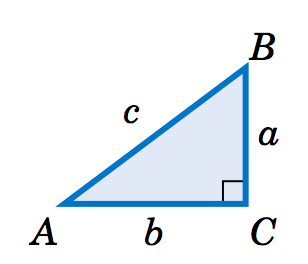
Figure 1.3.4
1.3.15 \(a = 5 \), \(b = 12\)
1.3.16 \(c = 6 \), \(B = 35^\circ\)
1.3.17 \(b = 2 \), \(A = 8^\circ\)
1.3.18 \(a = 2 \), \(c = 7\)
1.3.19 \(a = 3 \), \(A = 26^\circ\)
1.3.20 \(b = 1 \), \(c = 2\)
1.3.21 \(b = 3 \), \(B = 26^\circ\)
1.3.22 \(a = 2 \), \(B = 8^\circ\)
1.3.23 \(c = 2 \), \(A = 45^\circ\)
1.3.24 In Example 1.10 in Section 1.2, we found the exact values of all six trigonometric functions of \(75^\circ \). For example, we showed that \(\cot\;75^\circ = \frac{\sqrt{6} -
\sqrt{2}}{\sqrt{6} + \sqrt{2}} \). So since \(\tan\;15^\circ = \cot\;75^\circ \) by the Cofunction Theorem, this means that \(\tan\;15^\circ = \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}} \). We will now describe another method for finding the exact values of the trigonometric functions of \(15^\circ \). In fact, it can be used to find the exact values for the trigonometric functions of \(\frac{\theta}{2} \) when those for \(\theta \) are known, for any \(0^\circ < \theta < 90^\circ \). The method is illustrated in Figure 1.3.5 and is described below.
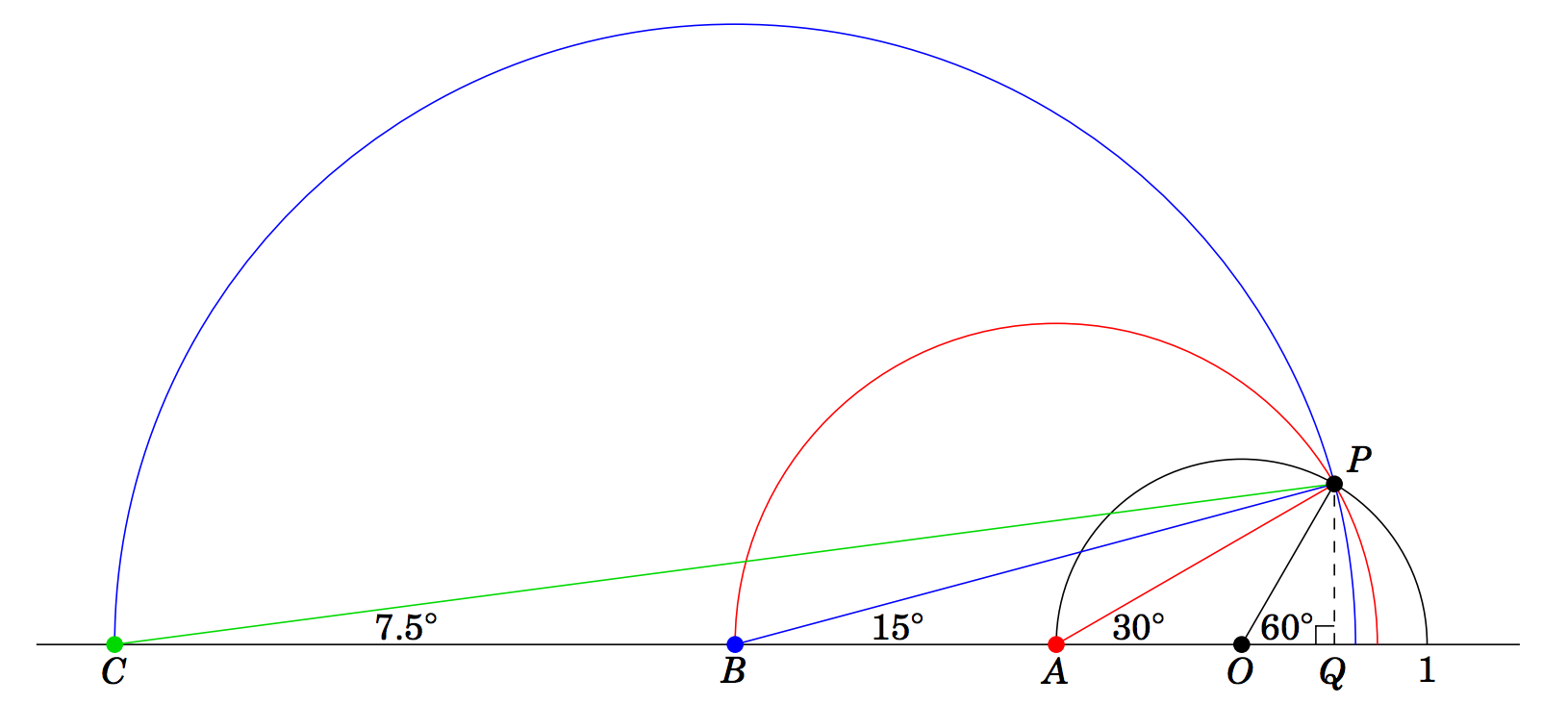
Figure 1.3.5
Draw a semicircle of radius \(1 \) centered at a point \(O \) on a horizontal line. Let \(P \) be the point on the semicircle such that \(\overline{OP} \) makes an angle of \(60^\circ \) with the horizontal line, as in Figure 1.3.5. Draw a line straight down from \(P \) to the horizontal line at the point \(Q \). Now create a second semicircle as follows: Let \(A \) be the left endpoint of the first semicircle, then draw a new semicircle centered at \(A \) with radius equal to \(AP \). Then create a third semicircle in the same way: Let \(B \) be the left endpoint of the second semicircle, then draw a new semicircle centered at \(B \) with radius equal to \(BP \).
This procedure can be continued indefinitely to create more semicircles. In general, it can be shown that the line segment from the center of the new semicircle to \(P \) makes an angle with the horizontal line equal to half the angle from the previous semicircle's center to \(P \).
(a) Explain why \(\angle\,PAQ=30^\circ \). (Hint: What is the supplement of \(60^\circ\)?)
(b) Explain why \(\angle\,PBQ=15^\circ \) and \(\angle\,PCQ=7.5^\circ \).
(c) Use Figure 1.3.5 to find the exact values of \(\sin\;15^\circ \), \(\cos\;15^\circ \), and \(\tan\;15^\circ \). (Hint: To start, you will need to use \(\angle\,POQ = 60^\circ\) and \(OP = 1 \) to find the exact lengths of \(\overline{PQ} \) and \(\overline{OQ} \).)
(d) Use Figure 1.3.5 to calculate the exact value of \(\tan\;7.5^\circ \).
(e) Use the same method but with an initial angle of \(\angle\,POQ = 45^\circ \) to find the exact values of \(\sin\;22.5^\circ \), \(\cos\;22.5^\circ \), and \(\tan\;22.5^\circ \).
1.3.25 A manufacturer needs to place ten identical ball bearings against the inner side of a circular container such that each ball bearing touches two other ball bearings, as in the picture on the right. The (inner) radius of the container is \(4 \) cm.
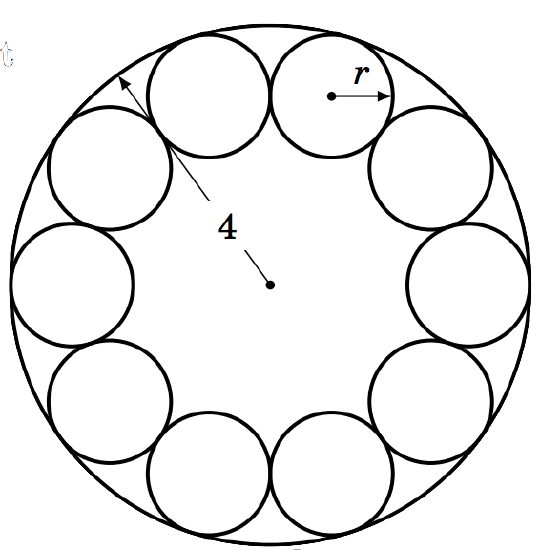
(a) Find the common radius \(r \) of the ball bearings.
(b) The manufacturer needs to place a circular ring\\inside the container. What is the largest possible (outer) radius of the ring such that it is not on top\\of the ball bearings and its base is level with the\\base of the container?
1.3.26 A circle of radius \(1 \) is inscribed inside a polygon with eight sides of equal length, called a regular octagon. That is, each of the eight sides is tangent to the circle, as in the picture on the right.
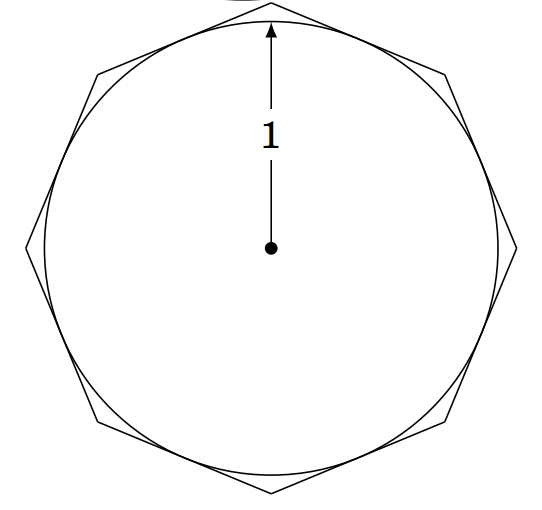
(a) Calculate the area of the octagon.
(b) If you were to increase the number of sides of the\\polygon, would the area inside it increase or decrease? What number would the area approach, if any? Explain.
(c) Inscribe a regular octagon inside the same circle. That is, draw a regular octagon such that each of its eight vertexes touches the circle. Calculate the area of this octagon.
1.3.27 The picture on the right shows a cube whose sides are of length \(a > 0 \).
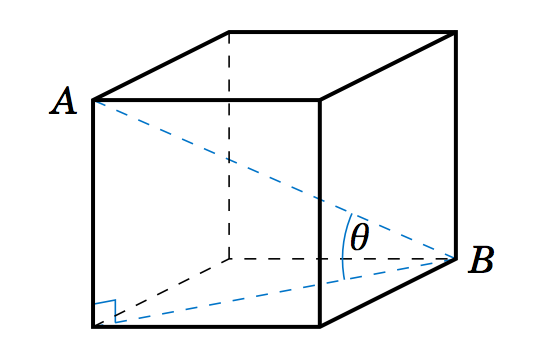
(a) Find the length of the diagonal line segment \(\overline{AB} \).
(b) Find the angle \(\theta \) that \(\overline{AB} \) makes with the base of the cube.
1.3.28 In Figure 1.3.6, suppose that \(\alpha \), \(\beta \), and \(AD \) are known. Show that:
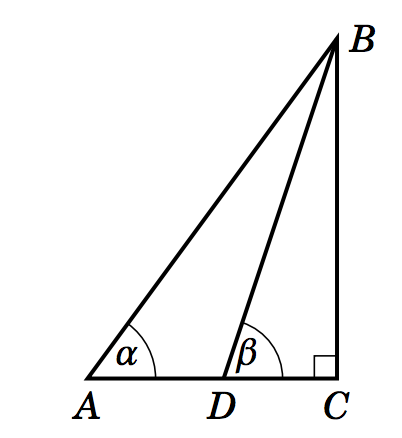
Figure 1.3.6
(a) \(BC ~=~ \dfrac{AD}{\cot\;\alpha - \cot\;\beta}\)
(b) \(AC ~=~ \dfrac{AD\;\cdot\;\tan\;\beta}{\tan\;\beta - \tan\;\alpha}\)
(c) \(BD ~=~ \dfrac{AD\;\cdot\;\sin\;\alpha}{\sin\;(\beta - \alpha)}\)
(Hint: What is the measure of the angle \(\angle\,ABD\;\)?)
1.3.29 Persons A and B are at the beach, their eyes are \(5 \) ft and \(6 \) ft, respectively, above sea level. How many miles farther out is Person B's horizon than Person A's? (Note: \(1 \) mile = \(5280\) ft)
1.4 Exercises
For Exercises 1-10, state in which quadrant or on which axis the given angle lies.
1.4.1 \(127^\circ\)
1.4.2 \(-127^\circ\)
1.4.3 \(313^\circ\)
1.4.4 \(-313^\circ\)
1.4.5 \(-90^\circ\)
1.4.6 \(621^\circ\)
1.4.7 \(230^\circ\)
1.4.8 \(2009^\circ\)
1.4.9 \(1079^\circ\)
1.4.10 \(-514^\circ\)
1.4.11 In which quadrant(s) do sine and cosine have the same sign?
1.4.12 In which quadrant(s) do sine and cosine have the opposite sign?
1.4.13 In which quadrant(s) do sine and tangent have the same sign?
1.4.14 In which quadrant(s) do sine and tangent have the opposite sign?
1.4.15 In which quadrant(s) do cosine and tangent have the same sign?
1.4.16 In which quadrant(s) do cosine and tangent have the opposite sign?
For Exercises 17-21, find the reference angle for the given angle.
1.4.17 \(317^\circ\)
1.4.18 \(63^\circ\)
1.4.19 \(-126^\circ\)
1.4.20 \(696^\circ\)
1.4.21 \(275^\circ\)
For Exercises 22-26, find the exact values of \(\sin\;\theta \) and \(\tan\;\theta \) when \(\cos\;\theta \) has the indicated value.
1.4.22 \(\cos\;\theta = \frac{1}{2}\)
1.4.23 \(\cos\;\theta = -\frac{1}{2}\)
1.4.24 \(\cos\;\theta = 0\)
1.4.25 \(\cos\;\theta = \frac{2}{5}\)
1.4.26 \(\cos\;\theta = 1\)
For Exercises 27-31, find the exact values of \(\cos\;\theta \) and \(\tan\;\theta \) when \(\sin\;\theta \) has the indicated value.
1.4.27 \(\sin\;\theta = \frac{1}{2}\)
1.4.28 \(\sin\;\theta = -\frac{1}{2}\)
1.4.29 \(\sin\;\theta = 0\)
1.4.30 \(\sin\;\theta = -\frac{2}{3}\)
1.4.31 \(\sin\;\theta = 1\)
For Exercises 32-36, find the exact values of \(\sin\;\theta \) and \(\cos\;\theta \) when \(\tan\;\theta \) has the indicated value.
1.4.32 \(\tan\;\theta = \frac{1}{2}\)
1.4.33 \(\tan\;\theta = -\frac{1}{2}\)
1.4.34 \(\tan\;\theta = 0\)
1.4.35 \(\tan\;\theta = \frac{5}{12}\)
1.4.36 \(\tan\;\theta = 1\)
For Exercises 37-40, use Table 1.3 to answer the following questions.
1.4.37 Does \(\sin\;180^\circ ~+~ \sin\;45^\circ ~=~ \sin\;225^\circ\;\)?
1.4.38 Does \(\tan\;300^\circ ~-~ \tan\;30^\circ ~=~ \tan\;270^\circ\;\)?
1.4.39 Does \(\cos\;180^\circ ~-~ \cos\;60^\circ ~=~ \cos\;120^\circ\;\)?
1.4.40 Does \(\cos\;240^\circ ~=~ (\cos\;120^\circ)^2 ~-~ (\sin\;120^\circ)^2 \;\)?
1.4.41 Expand Table 1.3 to include all integer multiples of \(15^\circ \). See Example 1.10 in Section 1.2.
1.5 Exercises
1.5.1 Let \(\theta = 32^\circ \). Find the angle between \(0^\circ \) and \(360^\circ \) which is the
(a) reflection of \(\theta \) around the \(x\)-axis
(b) reflection of \(\theta \) around the \(y\)-axis
(c) reflection of \(\theta \) around the origin
1.5.2 Repeat Exercise 1 with \(\theta = 248^\circ \).
1.5.3 Repeat Exercise 1 with \(\theta = -248^\circ \).
1.5.4 We proved Equations 1.4-1.6 for any angle \(\theta \) in QI. Mimic that proof to show that the formulas hold for \(\theta \) in QII.
1.5.5 Verify Equations 1.4-1.6 for \(\theta \) on the coordinate axes, i.e. for \(\theta = 0^\circ \), \(90^\circ \), \(180^\circ \), \(270^\circ \).
1.5.6 In Example 1.26 we used the formulas involving \(\theta + 90^\circ \) to prove that the slopes of perpendicular lines are negative reciprocals. Show that this result can also be proved using the formulas involving \(\theta - 90^\circ \). (Hint: Only the last paragraph in that example needs to be modified.)
For Exercises 7-14, find all angles \(0^\circ \le \theta < 360^\circ \) which satisfy the given equation:
1.5.7 \(\sin\;\theta = 0.4226\)
1.5.8 \(\sin\;\theta = 0.1909\)
1.5.9 \(\cos\;\theta = 0.4226\)
1.5.10 \(\sin\;\theta = 0\)
1.5.11 \(\tan\;\theta = 0.7813\)
1.5.12 \(\sin\;\theta = -0.6294\)
1.5.13 \(\cos\;\theta = -0.9816\)
1.5.14 \(\tan\;\theta = -9.514\)
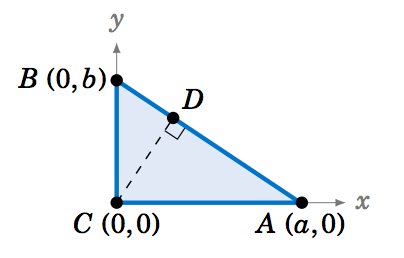
1.5.15 In our proof of the Pythagorean Theorem in Section 1.2, we claimed that in a right triangle \(\triangle\,ABC \) it was possible to draw a line segment \(\overline{CD} \) from the right angle vertex \(C \) to a point \(D \) on the hypotenuse \(\overline{AB} \) such that \(\overline{CD} \perp \overline{AB} \). Use the picture below to prove that claim. (Hint: Notice how \(\triangle\,ABC \) is placed on the \(xy\)-coordinate plane. What is the slope of the hypotenuse? What would be the slope of a line perpendicular to it?) Also, find the \((x,y) \) coordinates of the point \(D \) in terms of \(a \) and \(b \).
1.5.16 It can be proved without using trigonometric functions that the slopes of perpendicular lines are negative reciprocals. Let \(y = m_1{}x+b_1 \) and \(y = m_2{}x+b_2 \) be perpendicular lines (with nonzero slopes), as in the picture below. Use the picture to show that \(m_2 = -\frac{1}{m_1} \).(Hint: Think of similar triangles and the definition of slope.)
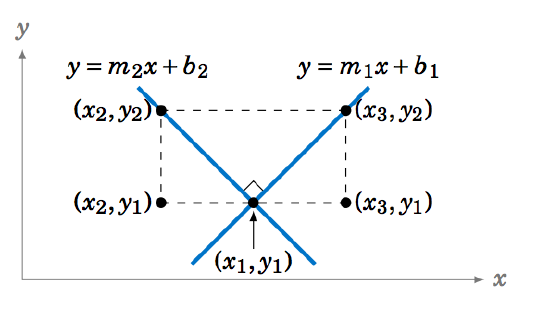
1.5.17 Prove Equations 1.19-1.21 by using Equations 1.10-1.12 and 1.13-1.15.


