3.E: Identities (Exercises)
- Page ID
- 3396
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany Corral's "Elementary Trigonometry" Textmap. This is a text on elementary trigonometry, designed for students who have completed courses in high-school algebra and geometry. Though designed for college students, it could also be used in high schools. The traditional topics are covered, but a more geometrical approach is taken than usual. Also, some numerical methods (e.g. the secant method for solving trigonometric equations) are discussed.
3.1 Exercises
3.1.1 We showed that \(\;\sin\;\theta ~=~ \pm\,\sqrt{1 ~-~ \cos^2 \;\theta}\; \) for all \(\theta \). Give an example of an angle \(\theta \) such that \(\sin\;\theta ~=~ -\sqrt{1 ~-~ \cos^2 \;\theta}\; \).
3.1.2 We showed that \(\;\cos\;\theta ~=~ \pm\,\sqrt{1 ~-~ \sin^2 \;\theta}\; \) for all \(\theta \). Give an example of an angle \(\theta \) such that \(\cos\;\theta ~=~ -\sqrt{1 ~-~ \sin^2 \;\theta}\; \).
3.1.3 Suppose that you are given a system of two equations of the following form:
\[\nonumber \begin{align*}
A\,\cos\;\phi ~ &= ~ B\, \nu_1 ~-~ B\nu_2 \;\cos\;\theta\\ \nonumber
A\,\sin\;\phi ~ &= ~ B\, \nu_2 \;\sin\;\theta ~.
\end{align*}\]
Show that \(\;A ^2 ~=~ B^2 \left( \nu_1^2 ~+~ \nu_2^2 ~-~ 2\nu_1 \nu_2 \;\cos\theta\ \right) \).
For Exercises 4-16, prove the given identity.
3.1.4 \(\cos\;\theta ~ \tan\;\theta ~=~ \sin\;\theta\)
3.1.5 \(\sin\;\theta ~ \cot\;\theta ~=~ \cos\;\theta\)
3.1.6 \(\dfrac{\tan\;\theta}{\cot\;\theta} ~=~ \tan^2 \;\theta\)
3.1.7 \(\dfrac{\csc\;\theta}{\sin\;\theta} ~=~ \csc^2 \;\theta\)
3.1.8 \(\dfrac{\cos^2 \;\theta}{1 ~+~ \sin\;\theta} ~=~ 1 ~-~ \sin\;\theta\)
3.1.9 \(\dfrac{1 ~-~ 2\;\cos^2 \;\theta}{\sin\;\theta ~ \cos\;\theta} ~=~ \tan\;\theta ~-~ \cot\;\theta\)
3.1.10 \(\sin^4 \;\theta ~-~ \cos^4 \;\theta ~=~ \sin^2 \;\theta ~-~ \cos^2 \;\theta\)
3.1.11 \(\cos^4 \;\theta ~-~ \sin^4 \;\theta ~=~ 1 ~-~ 2\;\sin^2 \;\theta\)
3.1.12 \(\dfrac{1 ~-~ \tan\;\theta}{1 ~+~ \tan\;\theta} ~=~
\dfrac{\cot\;\theta ~-~ 1}{\cot\;\theta ~+~ 1}\)
3.1.13 \(\dfrac{\tan\;\theta ~+~ \tan\;\phi}{\cot\;\theta ~+~ \cot\;\phi} ~=~
\tan\;\theta ~ \tan\;\phi\)
3.1.14 \(\dfrac{\sin^2 \;\theta}{1 ~-~ \sin^2 \;\theta} ~=~ \tan^2 \;\theta\)
3.1.15 \(\dfrac{1 ~-~ \tan^2 \;\theta}{1 ~-~ \cot^2 \;\theta} ~=~ 1 ~-~ \sec^2 \;\theta\)
3.1.16 \(\sin\;\theta ~=~ \pm\,\dfrac{\tan\;\theta}{\sqrt{1 ~+~
\tan^2 \;\theta}}\qquad \) (Hint: Solve for \(\;\sin^2 \theta\; \) in Exercise 14.)
3.1.17 Sometimes identities can be proved by geometrical methods. For example, to prove the identity in Exercise 16, draw an acute angle \(\theta \) in QI and pick the point \((1,y) \) on its terminal side, as in Figure 3.1.2. What must \(y \) equal? Use that to prove the identity for acute \(\theta \). Explain the adjustment(s) you would need to make in Figure 3.1.2 to prove the identity for \(\theta \) in the other quadrants. Does the identity hold if \(\theta \) is on either axis?
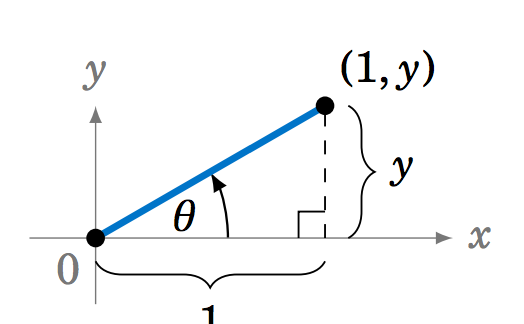
Figure 3.1.2
3.1.18 Similar to Exercise 16 , find an expression for \(\cos\;\theta \) solely in terms of \(\tan\;\theta \).
3.1.19 Find an expression for \(\tan\;\theta \) solely in terms of \(\sin\;\theta \), and one solely in terms of \(\cos\;\theta \).
3.1.20 Suppose that a point with coordinates \((x,y)=(a\;(\cos\;\psi\;-\;\epsilon),a\sqrt{1 - \epsilon^2}~\sin\;\psi)\) is a distance \(r>0 \) from the origin, where \(a>0 \) and \(0 < \epsilon < 1 \). Use \(\;r^2 = x^2 + y^2\) to show that \(\;r = a\;(1 \;-\; \epsilon\;\cos\;\psi)\; \).\\(Note: These coordinates arise in the study of elliptical orbits of planets.)
3.1.21 Show that each trigonometric function can be put in terms of the sine function.
3.2 Exercises
3.2.1 Verify the addition formulas 3.12 and 3.13 for \(A=B=0^\circ \).
For Exercises 2 and 3, find the exact values of \(\sin\;(A+B) \), \(\cos\;(A+B) \), and \(\tan\;(A+B) \).
3.2.2 \(\sin\;A = \frac{8}{17} \), \(\cos\;A = \frac{15}{17} \), \(\sin\;B = \frac{24}{25} \),
\(\cos\;B = \frac{7}{25}\)
3.2.3 \(\sin\;A = \frac{40}{41} \), \(\cos\;A = \frac{9}{41} \), \(\sin\;B = \frac{20}{29} \),
\(\cos\;B = \frac{21}{29}\)
3.2.4 Use \(75^\circ = 45^\circ + 30^\circ \) to find the exact value of \(\;\sin\;75^\circ \).
3.2.5 Use \(15^\circ = 45^\circ - 30^\circ \) to find the exact value of \(\;\tan\;15^\circ \).
3.2.6 Prove the identity \(\;\sin\;\theta + \cos\;\theta = \sqrt{2}\;\sin\;(\theta + 45^\circ)\; \). Explain why this shows that
\[\nonumber
-\sqrt{2} ~\le~ \;\sin\;\theta ~+~ \cos\;\theta ~\le~ \sqrt{2}
\]
for all angles \(\theta \). For which \(\theta \) between \(0^\circ \) and \(360^\circ \) would \(\;\sin\;\theta \;+\; \cos\;\theta\; \) be the largest?
For Exercises 7-14, prove the given identity.
3.2.7 \(\cos\;(A+B+C) \;=\; \cos\;A~\cos\;B~\cos\;C \;-\;
\cos\;A~\sin\;B~\sin\;C \;-\; \sin\;A~\cos\;B~\sin\;C \;-\; \sin\;A~\sin\;B~\cos\;C\)
3.2.8 \(\tan\;(A+B+C) ~=~ \dfrac{\tan\;A \;+\; \tan\;B \;+\; \tan\;C \;-\;
\tan\;A~\tan\;B~\tan\;C}{1 \;-\; \tan\;B~\tan\;C \;-\; \tan\;A~\tan\;C \;-\;
\tan\;A~\tan\;B}\)
3.2.9 \(\cot\;(A+B) ~=~ \dfrac{\cot\;A~\cot\;B \;-\; 1}{\cot\;A \;+\; \cot\;B}\)
3.2.10 \(\cot\;(A-B) ~=~ \dfrac{\cot\;A~\cot\;B \;+\; 1}{\cot\;B \;-\; \cot\;A}\)
3.2.11 \(\tan\;(\theta + 45^\circ) ~=~ \dfrac{1 \;+\; \tan\;\theta}{1 \;-\; \tan\;\theta}\)
3.2.12 \(\dfrac{\cos\;(A+B)}{\sin\;A~\cos\;B} ~=~ \cot\;A \;-\; \tan\;B\)
3.2.13 \(\cot\;A ~+~ \cot\;B ~=~ \dfrac{\sin\;(A+B)}{\sin\;A~\sin\;B}\)
3.2.14 \(\dfrac{\sin\;(A-B)}{\sin\;(A+B)} ~=~
\dfrac{\cot\;B \;-\; \cot\;A}{\cot\;B \;+\; \cot\;A}\)
3.2.15 Generalize Exercise 6: For any \(a \) and \(b \), \(-\sqrt{a^2 + b^2} \;\le\; a\;\sin\;\theta \;+\; b\;\cos\;\theta \;\le\; \sqrt{a^2 + b^2}\; \) for all \(\theta \).
3.2.16 Continuing Example 3.12, use Snell's law to show that the s-polarization transmission Fresnel coefficient
\[\tag{3.22}
t_{1\;2\;s} ~=~ \frac{2\;n_1 ~\cos\;\theta_1}{n_1 ~\cos\;\theta_1 ~+~ n_2 ~\cos\;\theta_2}
\]
can be written as:
\[\nonumber
t_{1\;2\;s} ~=~ \frac{2\;\cos\;\theta_1~\sin\;\theta_2}{\sin\;(\theta_2 + \theta_1)}
\]
3.2.17 Suppose that two lines with slopes \(m_1 \) and \(m_2 \), respectively, intersect at an angle \(\theta \) and are not perpendicular (i.e. \(\theta \ne 90^\circ\)), as in the figure on the right. Show that
\[\nonumber
\tan\;\theta ~=~ \left| \frac{m_1 ~-~ m_2}{1 ~+~ m_1 \; m_2} \right| ~.
\]
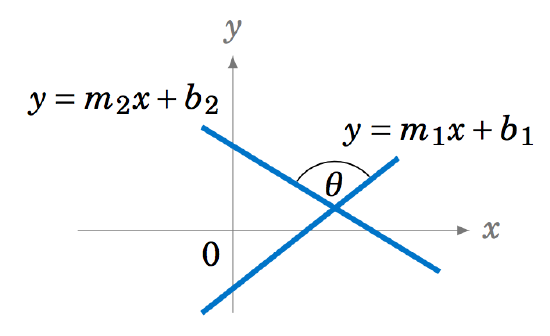
(Hint: Use Example 1.26 from Section 1.5.)
3.2.18 Use Exercise 17 to find the angle between the lines \(y=2x+3 \) and \(y=-5x-4 \).
3.2.19 For any triangle \(\triangle\,ABC \), show that \(\;\cot\;A~\cot\;B ~+~ \cot\;B~\cot\;C ~+~
\cot\;C~\cot\;A ~=~ 1 \).
(Hint: Use Exercise 9 and \(C=180^\circ - (A+B) \).)
3.2.20 For any positive angles \(A \), \(B \), and \(C \) such that \(A+B+C=90^\circ \), show that
\[\nonumber
\tan\;A~\tan\;B ~+~ \tan\;B~\tan\;C ~+~ \tan\;C~\tan\;A ~=~ 1 ~.
\]
3.2.21 Prove the identity \(\;\sin\;(A+B)~\cos\;B ~-~ \cos\;(A+B)~\sin\;B ~=~ \sin\;A \). Note that the right side depends only on \(A \), while the left side depends on both \(A \) and \(B \).
3.2.22 A line segment of length \(r > 0 \) from the origin to the point \((x,y) \) makes an angle \(\alpha \) with the positive \(x\)-axis, so that \((x,y) = (r\;\cos\;\alpha,r\;\sin\;\alpha) \), as in the figure below. What are the endpoint's new coordinates \((x',y') \) after a counterclockwise rotation by an angle \(\beta\;\)? Your answer should be in terms of \(r \), \(\alpha \), and \(\beta \).
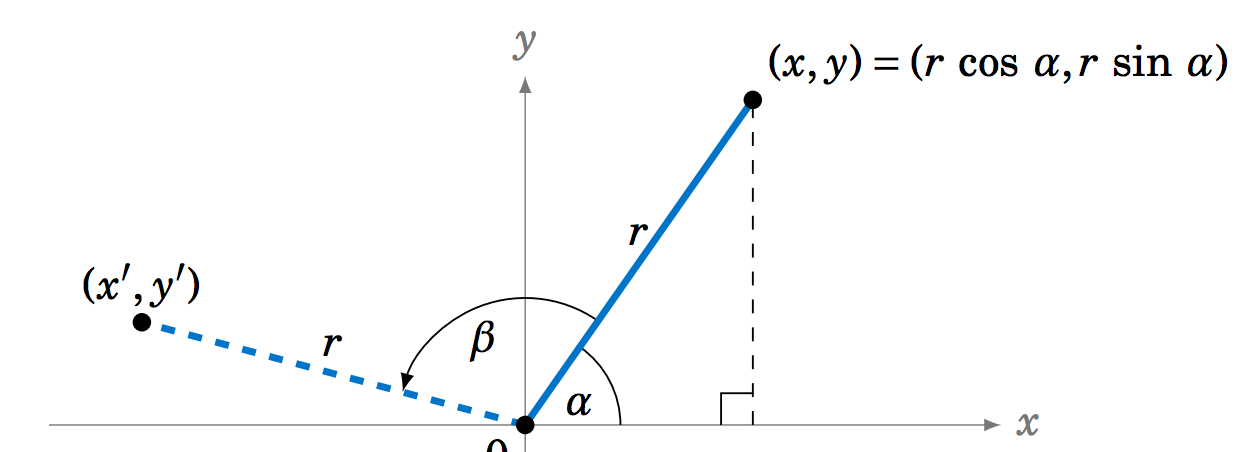
3.3 Exercises
For Exercises 1-8, prove the given identity.
3.3.1 \(\cos\;3\theta ~=~ 4\;\cos^3 \;\theta ~-~ 3\;\cos\;\theta\)
3.3.2 \(\tan\;\tfrac{1}{2}\theta ~=~ \csc\;\theta ~-~ \cot\;\theta\)
3.3.3 \(\dfrac{\sin\;2\theta}{\sin\;\theta} ~-~ \dfrac{\cos\;2\theta}{\cos\;\theta} ~=~ \sec\;\theta\)
3.3.4 \(\dfrac{\sin\;3\theta}{\sin\;\theta} ~-~ \dfrac{\cos\;3\theta}{\cos\;\theta} ~=~ 2\)
3.3.5 \(\tan\;2\theta ~=~ \dfrac{2}{\cot\;\theta \;-\; \tan\;\theta}\)
3.3.6 \(\tan\;3\theta ~=~ \dfrac{3\;\tan\;\theta \;-\; \tan^3 \;\theta}{1 \;-\; 3\;\tan^2 \;\theta}\)
3.3.7 \(\tan^2 \;\tfrac{1}{2}\theta ~=~ \dfrac{\tan\;\theta \;-\; \sin\;\theta}{\tan\;\theta \;+\; \sin\;\theta}\)
3.3.8 \(\dfrac{\cos^2 \;\psi}{\cos^2 \;\theta} ~=~ \dfrac{1 \;+\; \cos\;2\psi}{1 \;+\;
\cos\;2\theta}\)
3.3.9 Some trigonometry textbooks used to claim incorrectly that \(\;\sin\;\theta ~+~ \cos\;\theta ~=~ \sqrt{1 \;+\; \sin\;2\theta} \) was an identity. Give an example of a specific angle \(\theta \) that would make that equation false. Is \(\;\sin\;\theta ~+~ \cos\;\theta ~=~ \pm\;\sqrt{1 \;+\; \sin\;2\theta} \) an identity? Justify your answer.
3.3.10 Fill out the rest of the table below for the angles \(0^\circ < \theta < 720^\circ \) in increments of \(90^\circ \), showing \(\theta \), \(\tfrac{1}{2}\theta \), and the signs (\(+\) or \(-\)) of \(\sin\;\theta \) and \(\tan\;\tfrac{1}{2}\theta \).
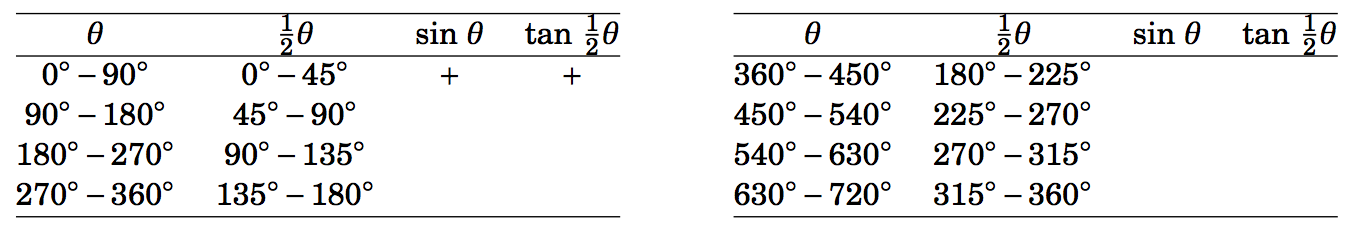
3.3.11 In general, what is the largest value that \(\;\sin\;\theta~\cos\;\theta\; \) can take? Justify your answer.
For Exercises 12-17, prove the given identity for any right triangle \(\triangle\,ABC \) with \(C=90^\circ \).
3.3.12 \(\sin\;(A-B) ~=~ \cos\;2B\)
3.3.13 \(\cos\;(A-B) ~=~ \sin\;2A\)
3.3.14 \(\sin\;2A ~=~ \dfrac{2\;ab}{c^2}\)
3.3.15 \(\cos\;2A ~=~ \dfrac{b^2 - a^2}{c^2}\)
3.3.16 \(\tan\;2A ~=~ \dfrac{2\;ab}{b^2 - a^2}\)
3.3.17 \(\tan\;\tfrac{1}{2}A ~=~ \dfrac{c - b}{a} ~=~ \dfrac{a}{c + b}\)
3.3.18 Continuing Exercise 20 from Section 3.1, it can be shown that
\[ \begin{align*}
r\;(1 \;-\; \cos\;\theta) ~&=~ a\;(1 \;+\; \epsilon)\,(1 \;-\; \cos\;\psi) ~,~\text{and}\\
r\;(1 \;+\; \cos\;\theta) ~&=~ a\;(1 \;-\; \epsilon)\,(1 \;+\; \cos\;\psi) ~,
\end{align*}\]
where \(\theta \) and \(\psi \) are always in the same quadrant. Show that \(\;\tan\;\tfrac{1}{2}\theta ~=~ \sqrt{\frac{1 \;+\; \epsilon}{1 \;-\; \epsilon}}~ \tan\;\tfrac{1}{2}\psi\; \).
3.4 Exercises
3.4.1 Prove formula 3.38.
3.4.2 Prove formula 3.39.
3.4.3 Prove formula 3.40.
3.4.4 Prove formula 3.41.
3.4.5 Prove formula 3.42.
3.4.6 Prove formula 3.44.
3.4.7 Prove Mollweide's second equation: For any triangle \(\triangle\,ABC \), \(~\dfrac{a+b}{c} ~=~ \dfrac{\cos\;\tfrac{1}{2}(A-B)}{\sin\;\tfrac{1}{2}C}\).
3.4.8 Continuing Example 3.21, use Snell's law to show that the p-polarization reflection Fresnel coefficient
\[\tag{3.46}
r_{1\;2\;p} ~=~ \frac{n_2 ~\cos\;\theta_1 ~-~ n_1 ~\cos\;\theta_2}{n_2 ~\cos\;\theta_1 ~+~
n_1 ~\cos\;\theta_2}
\]
can be written as:
\[
r_{1\;2\;p} ~=~ \frac{\tan\;(\theta_1 - \theta_2)}{\tan\;(\theta_1 + \theta_2)}
\]
3.4.9 There is a more general form for the instantaneous power \(p(t) = v(t)\;i(t) \) in an electrical circuit than the one in Example 3.22. The voltage \(v(t) \) and current \(i(t) \) can be given by
\[ \begin{align*}
v(t) ~&=~ V_m \;\cos\;(\omega t + \theta)~,\\
i(t) ~&=~ I_m \;\cos\;(\omega t + \phi)~,
\end{align*}\]
where \(\theta \) is called the phase angle. Show that \(p(t) \) can be written as
\[
p(t) ~=~ \tfrac{1}{2}\,V_m \; I_m \;\cos\;(\theta - \phi) ~+~
\tfrac{1}{2}\,V_m \; I_m \;\cos\;(2\omega t + \theta + \phi) ~.
\]
For Exercises 10-15, prove the given identity or inequality for any triangle \(\triangle\,ABC \).
3.4.10 \(\sin\;A \;+\; \sin\;B \;+\; \sin\;C ~=~
4\;\cos\;\tfrac{1}{2}A~\cos\;\tfrac{1}{2}B~\cos\;\tfrac{1}{2}C\) (Hint: Mimic Example 3.18 using \((\sin\;A \;+\; \sin\;B) \;+\; (\sin\;C \;-\; \sin\;(A+B+C)) \).)
3.4.11 \(\cos\;A \;+\; \cos\;(B-C) ~=~ 2\;\sin\;B~\sin\;C\)
3.4.12 \(\sin\;2A \;+\; \sin\;2B \;+\; \sin\;2C ~=~ 4\;\sin\;A~\sin\;B~\sin\;C\) (Hints: Group \(\sin\;2B \) and \(\sin\;2C \) together, use the double-angle formula for \(\sin\;2A \), use Exercise 11.)
3.4.13 \(\dfrac{a-b}{a+b} ~=~ \dfrac{\sin\;A \;-\; \sin\;B}{\sin\;A \;+\; \sin\;B}\)
3.4.14 \(\cos\;\tfrac{1}{2}A ~=~ \sqrt{\dfrac{s\;(s-a)}{bc}}~~ \) and \(~~\sin\;\tfrac{1}{2}A ~=~ \sqrt{\dfrac{(s-b)\;(s-c)}{bc}}\; \), \;where \(s=\tfrac{1}{2}(a+b+c)$\) (Hint: Use the Law of Cosines to show that \(2bc\;(1 + \cos\;A) ~=~ 4s\;(s-a) \).)
3.4.15 \(\tfrac{1}{2}\;(\sin\;A \;+\; \sin\;B) ~\le~
\sin\;\tfrac{1}{2}(A+B)\) (Hint: Show that \(\sin\;\tfrac{1}{2}(A+B) \;-\;
\tfrac{1}{2}\;(\sin\;A \;+\; \sin\;B) \;\ge\; 0 \).)
3.4.16 In Example 3.20, which angles \(A \), \(B \), \(C \) give the maximum value of \(\cos\;A \;+\; \cos\;B \;+\; \cos\;C\;\)?


