2.3E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 2.3E.1
In exercises 1 - 4, use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).
1) limx→0(4x2−2x+3)
- Answer
-
Use constant multiple law and difference law:
limx→0(4x2−2x+3)=4limx→0x2−2limx→0x+limx→03=0+0+3=3
2) limx→1x3+3x2+54−7x
3) limx→−2√x2−6x+3
- Answer
- Use root law: limx→−2√x2−6x+3=√limx→−2(x2−6x+3)=√19
4) limx→−1(9x+1)2
Exercise 2.3E.2
In exercises 5 - 10, use direct substitution to evaluate the limit of each continuous function.
5) limx→7x2
- Answer
- limx→7x2=49
6) limx→−2(4x2−1)
7) limx→011+sinx
- Answer
- limx→011+sinx=1
8) limx→2e2x−x2
9) limx→12−7xx+6
- Answer
- limx→12−7xx+6=−57
10) limx→3lne3x
Exercise 2.3E.3
In exercises 11 - 20, use direct substitution to show that each limit leads to the indeterminate form 0/0. Then, evaluate the limit analytically.
11) limx→4x2−16x−4
- Answer
- When x=4,x2−16x−4=16−164−4=00;
then, limx→4x2−16x−4=limx→4(x+4)(x−4)x−4=limx→4(x+4)=4+4=8
12) limx→2x−2x2−2x
13) limx→63x−182x−12
- Answer
- When x=6,3x−182x−12=18−1812−12=00;
then, limx→63x−182x−12=limx→63(x−6)2(x−6)=limx→632=32
14) limh→0(1+h)2−1h
15) limt→9t−9√t−3
- Answer
- When t=9,t−9√t−3=9−93−3=00;
then, limt→9t−9√t−3=limt→9t−9√t−3√t+3√t+3=limt→9(t−9)(√t+3)t−9=limt→9(√t+3)=√9+3=6
16) limh→01a+h−1ah, where a is a real-valued constant
17) \displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}
- Answer
- \displaystyle \text{When }θ = π, \quad\frac{\sin θ}{\tan θ}=\frac{\sin π}{\tan π}=\frac{0}{0};
then, \displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}=\lim_{θ→ π}\frac{\sin θ}{\frac{\sin θ}{\cos θ}}=\lim_{θ→π}\cos θ=\cos π=−1
18) \displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}
19) \displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}
- Answer
- \displaystyle \text{When }x=1/2, \quad\frac{2x^2+3x−2}{2x−1}=\frac{\frac{1}{2}+\frac{3}{2}−2}{1−1}=\frac{0}{0};
then, \displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\lim_{x→1/2}\frac{(2x−1)(x+2)}{2x−1}=\lim_{x→1/2}(x+2)=\frac{1}{2}+2=\frac{5}{2}
20) \displaystyle \lim_{x→−3}\frac{\sqrt{x+4}−1}{x+3}
Exercise \PageIndex{4}
In exercises 1 - 4, use direct substitution to obtain an undefined expression. Then, use the method used in Example 9 of this section to
In exercises 21 - 24, use direct substitution to obtain an undefined expression. Then, use the method used in Example 9 of this section to simplify the function and determine the limit.
21) \displaystyle \lim_{x→−2^−}\frac{2x^2+7x−4}{x^2+x−2}
- Answer
- −∞
22) \displaystyle \lim_{x→−2^+}\frac{2x^2+7x−4}{x^2+x−2}
23) \displaystyle \lim_{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}
- Answer
- −∞
24) \displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}
Exercise \PageIndex{5}
In exercises 1 - 8, assume that \displaystyle \lim_{x→6}f(x)=4,\quad \lim_{x→6}g(x)=9, and \displaystyle \lim_{x→6}h(x)=6. Use these three
In exercises 25 - 32, assume that \displaystyle \lim_{x→6}f(x)=4,\quad \lim_{x→6}g(x)=9, and \displaystyle \lim_{x→6}h(x)=6. Use these three facts and the limit laws to evaluate each limit.
25) \displaystyle \lim_{x→6}2f(x)g(x)
- Answer
- \displaystyle \lim_{x→6}2f(x)g(x)=2\left(\lim_{x→6}f(x)\right)\left(\lim_{x→6}g(x)\right)=2 (4)(9)=72
26) \displaystyle \lim_{x→6}\frac{g(x)−1}{f(x)}
27) \displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)
- Answer
- \displaystyle \lim_{x→6}\left(f(x)+\frac{1}{3}g(x)\right)=\lim_{x→6}f(x)+\frac{1}{3}\lim_{x→6}g(x)=4+\frac{1}{3}(9)=7
28) \displaystyle \lim_{x→6}\frac{\big(h(x)\big)^3}{2}
29) \displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}
- Answer
- \displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}=\sqrt{\lim_{x→6}g(x)−\lim_{x→6}f(x)}=\sqrt{9-4}=\sqrt{5}
30) \displaystyle \lim_{x→6}x⋅h(x)
31) \displaystyle \lim_{x→6}[(x+1)⋅f(x)]
- Answer
- \displaystyle \lim_{x→6}[(x+1)f(x)]=\left(\lim_{x→6}(x+1)\right)\left(\lim_{x→6}f(x)\right)=7(4)=28
32) \displaystyle \lim_{x→6}(f(x)⋅g(x)−h(x))
Exercise \PageIndex{6}
[T] In exercises 33 - 35, use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.
33) f(x)=\begin{cases}x^2, & x≤3\\ x+4, & x>3\end{cases}
a. \displaystyle \lim_{x→3^−}f(x)
b. \displaystyle \lim_{x→3^+}f(x)
- Answer
-
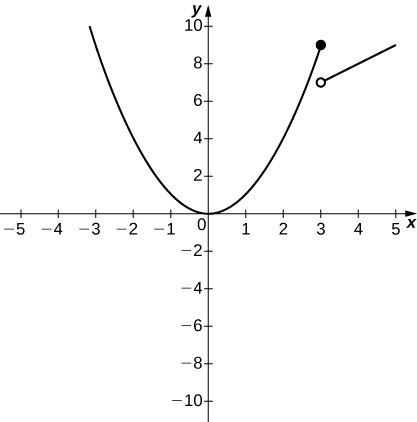
a. 9; b. 7
34) g(x)=\begin{cases}x^3−1, & x≤0\\1, & x>0\end{cases}
a. \displaystyle \lim_{x→0^−}g(x)
b. \displaystyle \lim_{x→0^+}g(x)
35) h(x)=\begin{cases}x^2−2x+1, & x<2\\3−x, & x≥2\end{cases}
a. \displaystyle \lim_{x→2^−}h(x)
b. \displaystyle \lim_{x→2^+}h(x)
Exercise \PageIndex{7}
In exercises 36 - 43, use the following graphs and the limit laws to evaluate each limit.
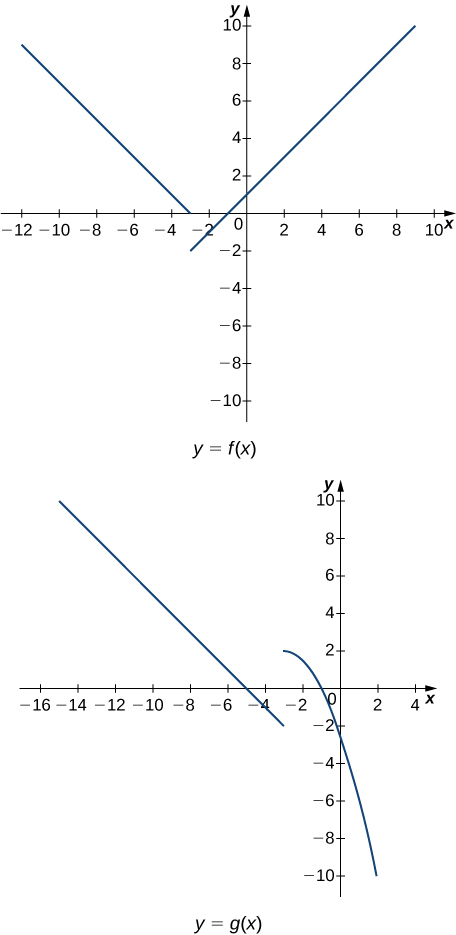
36) \displaystyle \lim_{x→−3^+}(f(x)+g(x))
37) \displaystyle \lim_{x→−3^−}(f(x)−3g(x))
- Answer
- \displaystyle \lim_{x→−3^−}(f(x)−3g(x))=\lim_{x→−3^−}f(x)−3\lim_{x→−3^−}g(x)=0+6=6
38) \displaystyle \lim_{x→0}\frac{f(x)g(x)}{3}
39) \displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}
- Answer
- \displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}=\frac{2+\left(\displaystyle \lim_{x→−5}g(x)\right)}{\displaystyle \lim_{x→−5}f(x)}=\frac{2+0}{2}=1
40) \displaystyle \lim_{x→1}(f(x))^2
41) \displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}
- Answer
- \displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}=\sqrt[3]{\lim_{x→1}f(x)−\lim_{x→1}g(x)}=\sqrt[3]{2+5}=\sqrt[3]{7}
42) \displaystyle \lim_{x→−7}(x⋅g(x))
43) \displaystyle \lim_{x→−9}[x⋅f(x)+2⋅g(x)]
- Answer
- \displaystyle \lim_{x→−9}(xf(x)+2g(x))=\left(\lim_{x→−9}x\right)\left(\lim_{x→−9}f(x)\right)+2\lim_{x→−9}g(x)=(−9)(6)+2(4)=−46
For exercises 44 - 46, evaluate the limit using the squeeze theorem. Use a calculator to graph the functions f(x), g(x), and h(x) when possible.
44) [T] True or False? If 2x−1≤g(x)≤x^2−2x+3, then \displaystyle \lim_{x→2}g(x)=0.
45) [T] \displaystyle \lim_{θ→0}θ^2\cos\left(\frac{1}{θ}\right)
- Answer
-
Since -1 \leq \cos(\dfrac{1}{\theta}) \leq 1 and \theta^2 \geq 0, -\theta^2 \leq \theta^2\cos(\dfrac{1}{\theta}) \leq \theta^2 . \\
Note that \lim_{\theta \to 0} \theta^2= - \lim_{\theta \to 0} \theta^2=0.
By squeeze theorem, \lim_{\theta \to 0} \theta^2\cos(\dfrac{1}{\theta})=0.
The limit is zero.
![The graph of three functions over the domain [-1,1], colored red, green, and blue as follows: red: theta^2, green: theta^2 * cos (1/theta), and blue: - (theta^2). The red and blue functions open upwards and downwards respectively as parabolas with vertices at the origin. The green function is trapped between the two.](https://math.libretexts.org/@api/deki/files/1926/CNX_Calc_Figure_02_03_206.jpeg?revision=1&size=bestfit&width=342&height=347)
46) \displaystyle \lim_{x→0}f(x), where f(x)=\begin{cases}0, & x\text{ rational}\\ x^2, & x\text{ irrrational}\end{cases}
Exercise \PageIndex{9}
47) [T] In physics, the magnitude of an electric field generated by a point charge at a distance r in a vacuum is governed by Coulomb’s law: E(r)=\dfrac{q}{4πε_0r^2}, where E represents the magnitude of the electric field, q is the charge of the particle, r is the distance between the particle and where the strength of the field is measured, and \dfrac{1}{4πε_0} is Coulomb’s constant: 8.988×109N⋅m^2/C^2.
a. Use a graphing calculator to graph E(r) given that the charge of the particle is q=10^{−10}.
b. Evaluate \displaystyle \lim_{r→0^+}E(r). What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?
- Answer
-
a.
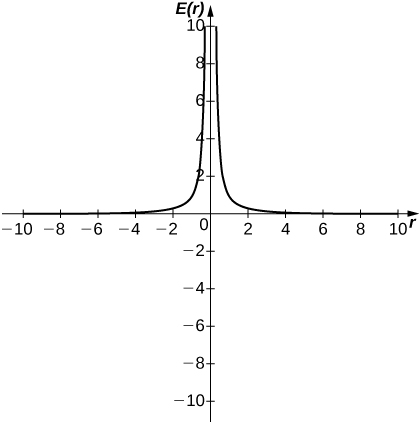
b. ∞. The magnitude of the electric field as you approach the particle q becomes infinite. It does not make physical sense to evaluate the negative distance.
48) [T] The density of an object is given by its mass divided by its volume: ρ=m/V.
a. Use a calculator to plot the volume as a function of density (V=m/ρ), assuming you are examining something of mass 8 kg (m=8).
b. Evaluate \displaystyle \lim_{x→0^+}V(\rho) and explain the physical meaning.
Exercise \PageIndex{10}
Evaluate the following:
- \displaystyle \lim\limits_{x\to3}x^2-3x+7
- \displaystyle \lim\limits_{x\to\pi}\left ( \frac{x-3}{x+5}\right )^7
- \displaystyle \lim\limits_{x\to3}4^{{x^3}-8x}
- \displaystyle \lim\limits_{x\to0}\ln (1+x)
- \displaystyle \lim\limits_{x\to\pi}\frac{x^2+3x+5}{5x^2-2x-3}
- \displaystyle \lim\limits_{x\to\pi}\frac{3x+1}{1-x}
- \displaystyle \lim\limits_{x\to6}\frac{x^2-4x-12}{x^2-13x+42}
- \displaystyle \lim\limits_{x\to0}\frac{x^2+2x}{x^2-2x}
- \displaystyle \lim\limits_{x\to2}\frac{x^2+6x-16}{x^2-3x+2}
- \displaystyle \lim\limits_{x\to2}\frac{x^2-5x-14}{x^2+10x+16}
- \displaystyle \lim\limits_{x\to-2}\frac{x^2-5x-14}{x^2+10x+16}
- \displaystyle \lim\limits_{x\to-1}\frac{x^2+9x+8}{x^2-6x-7}
- Answer
-
Under Construction
Exercise \PageIndex{11}
\displaystyle \lim_{x \to 0} \frac{\sqrt{x+4}-2}{x}
- Answer
-
\displaystyle \lim_{x \to 0} \frac{\sqrt{x+4}-2}{x} = \frac{\sqrt{0+4}-2}{0} =\left[\frac{0}{0}\right]
= \displaystyle \lim_{x \to 0} \frac{(\sqrt{x+4}-2) (\sqrt{x+4}+2)}{x (\sqrt{x+4}+2)}
= \displaystyle \lim_{x \to 0} \frac{((x+4)-4) }{x (\sqrt{x+4}+2)}
= \displaystyle \lim_{x \to 0} \frac{x }{x (\sqrt{x+4}+2)}
= \displaystyle \lim_{x \to 0} \frac{1 }{(\sqrt{x+4}+2)}= \frac{1 }{(\sqrt{0+4}+2)}= \frac{1 }{4}.
Exercise \PageIndex{12}
Evaluate the following limits:
1. \displaystyle \lim\limits_{x \to 4}\frac{1}{|4-x|}
- Answer
-
\displaystyle \infty
2. \displaystyle \lim\limits_{x \to -1^-}\sqrt{1-x^2}
- Answer
-
DNE
3. \displaystyle \lim\limits_{x \to -1^+}\sqrt{1-x^2}
- Answer
-
0
4. \displaystyle \lim\limits_{x \to 2}\frac{|x-2|}{x^2+x-6}
- Answer
-
\displaystyle \mbox{dne}
5. \displaystyle \lim\limits_{x \to 2}\frac{\frac{1}{x}-\frac{1}{2}}{x-2}
- Answer
-
\displaystyle \frac{1}{4}
6. \displaystyle f(x)=\begin{cases} x^2 & \mbox{if } x \leq 1 \\ 2x & \mbox{if } x > 1\end{cases}
- Answer
-
Under Construction
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Pamini Thangarajah (Mount Royal University, Calgary, Alberta, Canada)

