2.1: Integration by parts
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Here's a simple integral that we can't yet evaluate:
∫xcosxdx.
It's a simple matter to take the derivative of the integrand using the Product Rule, but there is no Product Rule for integrals. However, this section introduces Integration by Parts, a method of integration that is based on the Product Rule for derivatives. It will enable us to evaluate this integral.
The Product Rule says that if u and v are functions of x, then (uv)′=u′v+uv′. For simplicity, we've written u for u(x) and v for v(x). Suppose we integrate both sides with respect to x. This gives
∫(uv)′dx=∫(u′v+uv′)dx.
By the Fundamental Theorem of Calculus, the left side integrates to uv. The right side can be broken up into two integrals, and we have
uv=∫u′vdx+∫uv′dx.
Solving for the second integral we have
∫uv′dx=uv−∫u′vdx.
Using differential notation, we can write du=u′(x)dx and dv=v′(x)dx and the expression above can be written as follows:
∫udv=uv−∫vdu.
This is the Integration by Parts formula. For reference purposes, we state this in a theorem.
Theorem 2.1.1: Integration by Parts
Let u and v be differentiable functions of x on an interval I containing a and b. Then
∫u dv=uv−∫v du,
and integration by parts
∫x=bx=au dv=uv|ba−∫x=bx=av du.
Let's try an example to understand our new technique.
Example 2.1.1: Integrating using Integration by Parts
Evaluate ∫xcosx dx.
Solution
The key to Integration by Parts is to identify part of the integrand as "u" and part as "dv." Regular practice will help one make good identifications, and later we will introduce some principles that help. For now, let u=x and dv=cosx dx.
It is generally useful to make a small table of these values as done below. Right now we only know u and dv as shown on the left of Figure 2.1.1; on the right we fill in the rest of what we need. If u=x, then du=dx. Since dv=cosx dx, v is an antiderivative of cosx. We choose v=sinx.
Now substitute all of this into the Integration by Parts formula, giving∫xcosxdx=xsinx−∫sinxdx.
We can then integrate sinx to get −cosx+C and overall our answer is
∫xcosx dx=xsinx+cosx+C.
Note how the antiderivative contains a product, xsinx. This product is what makes Integration by Parts necessary.
The example above demonstrates how Integration by Parts works in general. We try to identify u and dv in the integral we are given, and the key is that we usually want to choose u and dv so that du is simpler than u and v is hopefully not too much more complicated than dv. This will mean that the integral on the right side of the Integration by Parts formula, ∫vdu will be simpler to integrate than the original integral ∫udv.
In the example above, we chose u=x and dv=cosxdx. Then du=dx was simpler than u and v=sinx is no more complicated than dv. Therefore, instead of integrating xcosxdx, we could integrate sinxdx, which we knew how to do.
A useful mnemonic for helping to determine u is "LIATE," where
L=Logarithmic,I=InverseTrig.,A=Algebraic(polynomials),
T=Trigonometric,andE=Exponential.
If the integrand contains both a logarithmic and an algebraic term, in general letting u be the logarithmic term works best, as indicated by L coming before A in LIATE.
We now consider another example.
Example 2.1.2: Integrating using Integration by Parts
Evaluate ∫xexdx.
Solution
The integrand contains an Algebraic term (x) and an \textbf{E}xponential term (ex). Our mnemonic suggests letting u be the algebraic term, so we choose u=x and dv=exdx. Then du=dx and v=ex as indicated by the tables below.
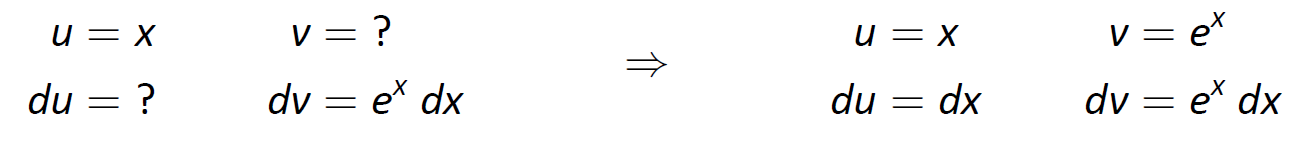
We see du is simpler than u, while there is no change in going from dv to v. This is good. The Integration by Parts formula gives
∫xexdx=xex−∫exdx.
The integral on the right is simple; our final answer is
∫xex dx=xex−ex+C.
Note again how the antiderivatives contain a product term.
Example 2.1.3: Integrating using Integration by Parts
Evaluate ∫x2cosxdx.
Solution
The mnemonic suggests letting u=x2 instead of the trigonometric function, hence dv=cosxdx. Then du=2xdx and v=sinx as shown below.
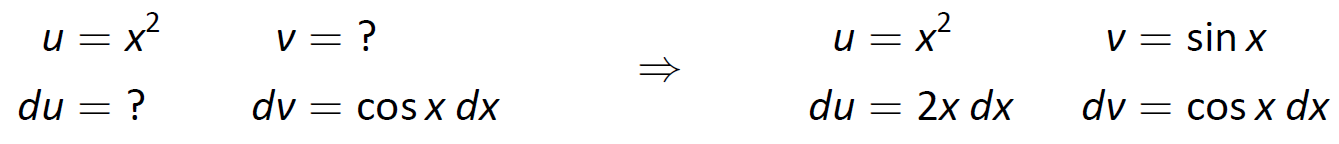
The Integration by Parts formula gives
∫x2cosxdx=x2sinx−∫2xsinxdx.
At this point, the integral on the right is indeed simpler than the one we started with, but to evaluate it, we need to do Integration by Parts again. Here we choose u=2x and dv=sinx and fill in the rest below.
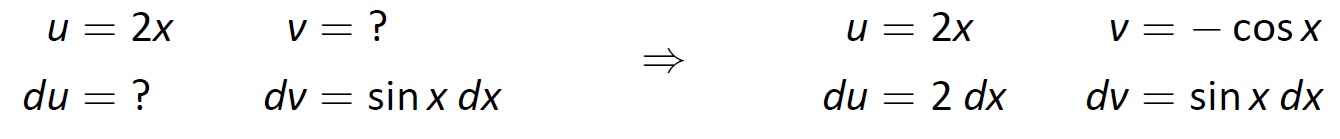
The integral all the way on the right is now something we can evaluate. It evaluates to −2sinx. Then going through and simplifying, being careful to keep all the signs straight, our answer is
∫x2cosx dx=x2sinx+2xcosx−2sinx+C.
Example 2.1.4: Integrating using Integration by Parts
Evaluate ∫excosxdx.
Solution
This is a classic problem. Our mnemonic suggests letting u be the trigonometric function instead of the exponential. In this particular example, one can let u be either cosx or ex; to demonstrate that we do not have to follow LIATE, we choose u=ex and hence dv=cosxdx. Then du=exdx and v=sinx as shown below.
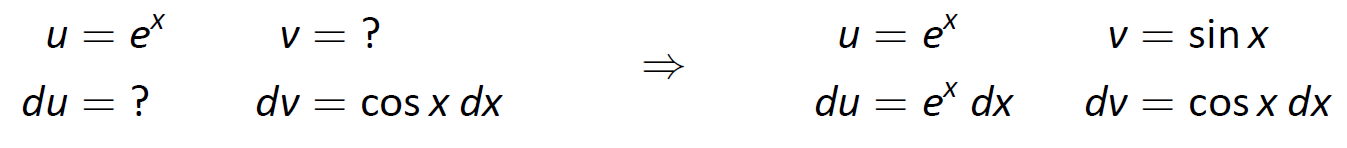
Notice that du is no simpler than u, going against our general rule (but bear with us). The Integration by Parts formula yields
∫excosx dx=exsinx−∫exsinxdx.
The integral on the right is not much different than the one we started with, so it seems like we have gotten nowhere. Let's keep working and apply Integration by Parts to the new integral, using u=ex and dv=sinxdx. This leads us to the following:
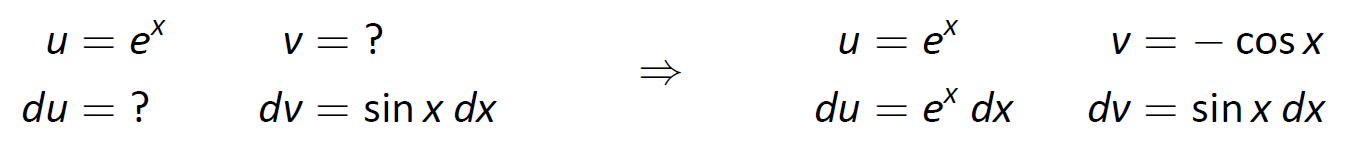
The Integration by Parts formula then gives:
∫excosxdx=exsinx−(−excosx−∫−excosxdx)=exsinx+excosx−∫excosx dx.
It seems we are back right where we started, as the right hand side contains ∫excosxdx. But this is actually a good thing.
Add ∫excosx dx to both sides. This gives
2∫excosx dx=exsinx+excosxNow divide both sides by 2:∫excosx dx=12(exsinx+excosx).
Simplifying a little and adding the constant of integration, our answer is thus
∫excosx dx=12ex(sinx+cosx)+C.
Example 2.1.5: Integrating using Integration by Parts: antiderivative of lnx
Evaluate ∫lnxdx.
Solution
One may have noticed that we have rules for integrating the familiar trigonometric functions and ex, but we have not yet given a rule for integrating lnx. That is because lnx can't easily be integrated with any of the rules we have learned up to this point. But we can find its antiderivative by a clever application of Integration by Parts. Set u=lnx and dv=dx. This is a good, sneaky trick to learn as it can help in other situations. This determines du=(1/x)dx and v=x as shown below.
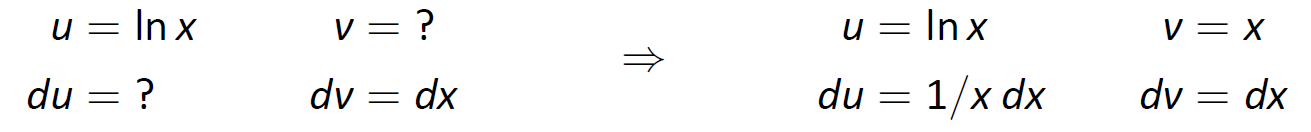
Putting this all together in the Integration by Parts formula, things work out very nicely:
∫lnxdx=xlnx−∫x1xdx.
The new integral simplifies to ∫1dx, which is about as simple as things get. Its integral is x+C and our answer is
∫lnx dx=xlnx−x+C.
Example 2.1.6: Integrating using Int. by Parts: antiderivative of arctanx=tan−1x
Evaluate ∫arctanxdx.
Solution
The same sneaky trick we used above works here. Let u=arctanx and dv=dx. Then du=1/(1+x2)dx and v=x. The Integration by Parts formula gives
∫arctanxdx=xarctanx−∫x1+x2dx.
The integral on the right can be solved by substitution. Taking u=1+x2, we get du=2xdx. The integral then becomes
∫arctanxdx=xarctanx−12∫1udu.
The integral on the right evaluates to ln|u|+C, which becomes ln(1+x2)+C. Therefore, the answer is
∫arctanx dx=xarctanx−ln(1+x2)+C.
Example 2.1.1:
Evaluate ∫xarctan(3x)dx.
Substitution Before Integration
When taking derivatives, it was common to employ multiple rules (such as using both the Quotient and the Chain Rules). It should then come as no surprise that some integrals are best evaluated by combining integration techniques. In particular, here we illustrate making an "unusual" substitution first before using Integration by Parts.
Example 2.1.7: Integration by Parts after substitution
Evaluate ∫cos(lnx) dx.
Solution
The integrand contains a composition of functions, leading us to think Substitution would be beneficial. Letting u=lnx, we have du=1/x dx. This seems problematic, as we do not have a 1/x in the integrand. But consider:
du=1x dx⇒x⋅du=dx.
Since u=lnx, we can use inverse functions and conclude that x=eu. Therefore we have that
dx=x⋅du=eu du.
We can thus replace lnx with u and dx with eu du. Thus we rewrite our integral as
∫cos(lnx) dx=∫eucosu du.
We evaluated this integral in Example 2.1.4. Using the result there, we have:
∫cos(lnx) dx=∫eucosu du=12eu(sinu+cosu)+C=12elnx(sin(lnx)+cos(lnx))+C=12x(sin(lnx)+cos(lnx))+C.
Definite Integrals and Integration By Parts
So far we have focused only on evaluating indefinite integrals. Of course, we can use Integration by Parts to evaluate definite integrals as well, as Theorem 2.1.1 states. We do so in the next example.
Example 2.1.8: Definite integration using Integration by Parts
Evaluate ∫21x2lnxdx.
Solution
Our mnemonic suggests letting u=lnx, hence dv=x2dx.
We then get du=(1/x)dx and v=x3/3 as shown below.
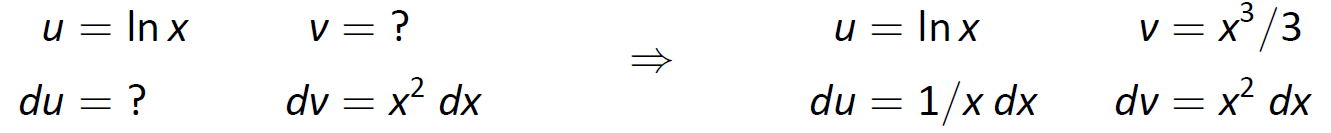
The Integration by Parts formula then gives
∫21x2lnxdx=x33lnx|21−∫21x331xdx=x33lnx|21−∫21x23dx=x33lnx|21−x39|21=(x33lnx−x39)|21=(83ln2−89)−(13ln1−19)=83ln2−79≈1.07.
In general, Integration by Parts is useful for integrating certain products of functions, like ∫xexdx or ∫x3sinxdx. It is also useful for integrals involving logarithms and inverse trigonometric functions.
As stated before, integration is generally more difficult than derivation. We are developing tools for handling a large array of integrals, and experience will tell us when one tool is preferable/necessary over another. For instance, consider the three similar--looking integrals
∫xexdx,∫xex2dxand∫xex3dx.
While the first is calculated easily with Integration by Parts, the second is best approached with Substitution. Taking things one step further, the third integral has no answer in terms of elementary functions, so none of the methods we learn in calculus will get us the exact answer.
Integration by Parts is a very useful method, second only to substitution. In the following sections of this chapter, we continue to learn other integration techniques. The next section focuses on handling integrals containing trigonometric functions.
Contributors
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Integrated by Justin Marshall.
Integration by parts (IBP)
∫udv=uv−∫vdu.
Note
When deciding which function should be u and dv, it is best to choose u as the function that will simplify easily.
The priority for choosing u is:
1. u=lnx
2. u=xn, where n= integer
3. u=enx, where n= integer
Example 2.1.1:
Find ∫x2e−xdx.
- Answer
-
Using the priority listed above, let u=x2 and dv=e−xdx.
Since u=x2 , du=2x.
Since dv=e−x, \(v= \int e^{-x} \, dx).
=−e−x
Using the IBP,
∫udv=uv−∫vdu
=x2e−x −∫e−x2xdx
=lnxx22 −12∫ xdx
=lnxx22 −12x22
=lnxx22 −x24
Simplifying the answer,
∫xlnxdx=x22(lnx−12)+C
Reminder: Make sure to write + C at the end of the answer as C is a constant.
Example 2.1.2:
Find ∫xlnxdx.
- Answer
-
Using the priority listed above, let u=lnx and dv=xdx.
Since u=lnx , du=1x.
Since dv=x, v=x22.
Using the IBP,
∫udv=uv−∫vdu
=lnxx22 −∫x22xdx
=lnxx22 −12∫ xdx
=lnxx22 −12x22
=lnxx22 −x24
Simplifying the answer,
∫xlnxdx=x22(lnx−12)+C
Reminder: Make sure to write + C at the end of the answer as C is a constant.
Example 2.1.3:
Find ∫lnxdx.
- Answer
-
Add texts here. Do not delete this text first.
Exercise 2.1.1
Add exercises text here. For the automatic number to work, you need to add the "AutoNum" template (preferably at the end) to the page.
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.


