10.5: Areas and Lengths in Polar Coordinates
- Page ID
- 8196
- Apply the formula for area of a region in polar coordinates.
- Determine the arc length of a polar curve.
In the rectangular coordinate system, the definite integral provides a way to calculate the area under a curve. In particular, if we have a function \(y=f(x)\) defined from \(x=a\) to \(x=b\) where \(f(x)>0\) on this interval, the area between the curve and the x-axis is given by
\[A=\int ^b_af(x)dx. \nonumber \]
This fact, along with the formula for evaluating this integral, is summarized in the Fundamental Theorem of Calculus. Similarly, the arc length of this curve is given by
\[L=\int ^b_a\sqrt{1+(f′(x))^2}dx. \nonumber \]
In this section, we study analogous formulas for area and arc length in the polar coordinate system.
Areas of Regions Bounded by Polar Curves
We have studied the formulas for area under a curve defined in rectangular coordinates and parametrically defined curves. Now we turn our attention to deriving a formula for the area of a region bounded by a polar curve. Recall that the proof of the Fundamental Theorem of Calculus used the concept of a Riemann sum to approximate the area under a curve by using rectangles. For polar curves we use the Riemann sum again, but the rectangles are replaced by sectors of a circle.
Consider a curve defined by the function \(r=f(θ),\) where \(α≤θ≤β.\) Our first step is to partition the interval \([α,β]\) into n equal-width subintervals. The width of each subinterval is given by the formula \(Δθ=(β−α)/n\), and the ith partition point \(θ_i\) is given by the formula \(θ_i=α+iΔθ\). Each partition point \(θ=θ_i\) defines a line with slope \(\tan θ_i\) passing through the pole as shown in the following graph.
The line segments are connected by arcs of constant radius. This defines sectors whose areas can be calculated by using a geometric formula. The area of each sector is then used to approximate the area between successive line segments. We then sum the areas of the sectors to approximate the total area. This approach gives a Riemann sum approximation for the total area. The formula for the area of a sector of a circle is illustrated in the following figure.
Recall that the area of a circle is \(A=πr^2\). When measuring angles in radians, 360 degrees is equal to \(2π\) radians. Therefore a fraction of a circle can be measured by the central angle \(θ\). The fraction of the circle is given by \(\dfrac{θ}{2π}\), so the area of the sector is this fraction multiplied by the total area:
\[A=(\dfrac{θ}{2π})πr^2=\dfrac{1}{2}θr^2. \nonumber \]
Since the radius of a typical sector in Figure \(\PageIndex{1}\) is given by \(r_i=f(θ_i)\), the area of the ith sector is given by
\[A_i=\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]
Therefore a Riemann sum that approximates the area is given by
\[A_n=\sum_{i=1}^nA_i≈\sum_{i=1}^n\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]
We take the limit as \(n→∞\) to get the exact area:
\[A=\lim_{n→∞}A_n=\dfrac{1}{2}\int ^β_α(f(θ))^2dθ. \nonumber \]
This gives the following theorem.
Suppose \(f\) is continuous and nonnegative on the interval \(α≤θ≤β\) with \(0<β−α≤2π\). The area of the region bounded by the graph of \(r=f(θ)\) between the radial lines \(θ=α\) and \(θ=β\) is
\[\begin{align} A =\dfrac{1}{2}\int ^β_α[f(θ)]^2 dθ \\[4pt] =\dfrac{1}{2}\int ^β_αr^2 dθ. \label{areapolar}\end{align} \]
Find the area of one petal of the rose defined by the equation \(r=3\sin(2θ).\)
Solution
The graph of \(r=3\sin (2θ)\) follows.
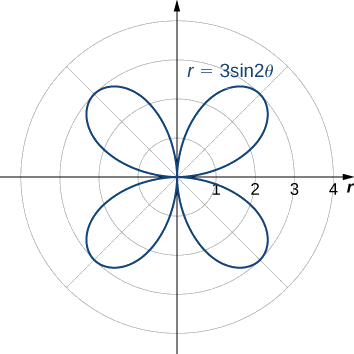
When \(θ=0\) we have \(r=3\sin(2(0))=0\). The next value for which \(r=0\) is \(θ=π/2\). This can be seen by solving the equation \(3\sin (2θ)=0\) for \(θ\). Therefore the values \(θ=0\) to \(θ=π/2\) trace out the first petal of the rose. To find the area inside this petal, use Equation \ref{areapolar} with \(f(θ)=3\sin (2θ), α=0,\) and \(β=π/2\):
\[\begin{align*} A &=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_0[3\sin (2θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ. \end{align*}\]
To evaluate this integral, use the formula \(\sin^2α=(1−\cos (2α))/2\) with \(α=2θ:\)
\[\begin{align*} A &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ \\[4pt] &=\dfrac{9}{2}\int ^{π/2}_0\dfrac{(1−\cos(4θ))}{2}dθ \\[4pt] &=\dfrac{9}{4}(\int ^{π/2}_01−\cos(4θ)dθ) \\[4pt] &=\dfrac{9}{4}(θ−\dfrac{\sin(4θ)}{4}∣^{π/2}_0 \\[4pt] &=\dfrac{9}{4}(\dfrac{π}{2}−\dfrac{\sin 2π}{4})−\dfrac{9}{4}(0−\dfrac{\sin 4(0)}{4}) \\[4pt] &=\dfrac{9π}{8}\end{align*}\]
Find the area inside the cardioid defined by the equation \(r=1−\cos θ\).
- Hint
-
Use Equation \ref{areapolar}. Be sure to determine the correct limits of integration before evaluating.
- Answer
-
\(A=3π/2\)
Example \(\PageIndex{1}\) involved finding the area inside one curve. We can also use Equation \ref{areapolar} to find the area between two polar curves. However, we often need to find the points of intersection of the curves and determine which function defines the outer curve or the inner curve between these two points.
Find the area outside the cardioid \(r=2+2\sin θ\) and inside the circle \(r=6\sin θ\).
Solution
First draw a graph containing both curves as shown.
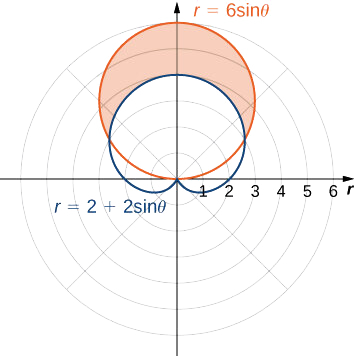
To determine the limits of integration, first find the points of intersection by setting the two functions equal to each other and solving for \(θ\):
\[\begin{align*} 6 \sin θ &=2+2\sin θ \\[4pt] 4\sin θ &=2 \\[4pt] \sin θ &=\dfrac{1}{2} \end{align*}. \nonumber \]
This gives the solutions \(θ=\dfrac{π}{6}\) and \(θ=\dfrac{5π}{6}\), which are the limits of integration. The circle \(r=3\sin θ\) is the red graph, which is the outer function, and the cardioid \(r=2+2\sin θ\) is the blue graph, which is the inner function. To calculate the area between the curves, start with the area inside the circle between \(θ=\dfrac{π}{6}\) and \(θ=\dfrac{5π}{6}\), then subtract the area inside the cardioid between \(θ=\dfrac{π}{6}\) and \(θ=\dfrac{5π}{6}\):
\(A=\text{circle}−\text{cardioid}\)
\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}[6\sin θ]^2dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}[2+2\sin θ]^2dθ\)
\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}36\sin^2θ\,dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}4+8\sin θ+4\sin^2θ\,dθ\)
\(=18\int ^{5π/6}_{π/6}\dfrac{1−\cos(2θ)}{2}dθ−2\int ^{5π/6}_{π/6}1+2\sin θ+\dfrac{1−\cos(2θ)}{2}dθ\)
\(=9[θ−\dfrac{\sin(2θ)}{2}]^{5π/6}_{π/6}−2[\dfrac{3θ}{2}−2\cos θ−\dfrac{\sin(2θ)}{4}]^{5π/6}_{π/6}\)
\(=9(\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})−9(\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})−(3(\dfrac{5π}{6})−4\cos\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})+(3(\dfrac{π}{6})−4\cos\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})\)
\(=4π\).
Find the area inside the circle \(r=4\cos θ\) and outside the circle \(r=2\).
- Hint
-
Use Equation \ref{areapolar} and take advantage of symmetry.
- Answer
-
\(A=\dfrac{4π}{3}+2\sqrt{3}\)
In Example \(\PageIndex{2}\) we found the area inside the circle and outside the cardioid by first finding their intersection points. Notice that solving the equation directly for \(θ\) yielded two solutions: \(θ=\dfrac{π}{6}\) and \(θ=\dfrac{5π}{6}\). However, in the graph there are three intersection points. The third intersection point is the origin. The reason why this point did not show up as a solution is because the origin is on both graphs but for different values of \(θ\). For example, for the cardioid we get
\[\begin{align*} 2+2\sin θ =0 \\[4pt] \sin θ =−1 ,\end{align*}. \nonumber \]
so the values for \(θ\) that solve this equation are \(θ=\dfrac{3π}{2}+2nπ\), where \(n\) is any integer. For the circle we get
\[6\sin θ=0. \nonumber \]
The solutions to this equation are of the form \(θ=nπ\) for any integer value of \(n\). These two solution sets have no points in common. Regardless of this fact, the curves intersect at the origin. This case must always be taken into consideration.
Arc Length in Polar Curves
Here we derive a formula for the arc length of a curve defined in polar coordinates. In rectangular coordinates, the arc length of a parameterized curve \((x(t),y(t))\) for \(a≤t≤b\) is given by
\[L=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt. \nonumber \]
In polar coordinates we define the curve by the equation \(r=f(θ)\), where \(α≤θ≤β.\) In order to adapt the arc length formula for a polar curve, we use the equations
\[x=r\cos θ=f(θ)\cos θ \nonumber \]
and
\[y=r\sin θ=f(θ)\sin θ, \nonumber \]
and we replace the parameter \(t\) by \(θ\). Then
\[\dfrac{dx}{dθ}=f′(θ)\cos θ−f(θ)\sin θ \nonumber \]
\[\dfrac{dy}{dθ}=f′(θ)\sin θ+f(θ)\cos θ. \nonumber \]
We replace \(dt\) by \(dθ\), and the lower and upper limits of integration are \(α\) and \(β\), respectively. Then the arc length formula becomes
\[ \begin{align*} L &=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \\[4pt] &=\int ^β_α\sqrt{\left(\dfrac{dx}{dθ}\right)^2+\left(\dfrac{dy}{dθ}\right)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ)\cos θ−f(θ)\sin θ)^2+(f′(θ)\sin θ+f(θ)\cos θ)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2(\cos^2 θ+\sin^2 θ)+(f(θ))^2(\cos^2 θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2+(f(θ))^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ \end{align*}\]
This gives us the following theorem.
Let \(f\) be a function whose derivative is continuous on an interval \(α≤θ≤β\). The arc length of the graph of \(r=f(θ)\) from \(θ=α\) to \(θ=β\) is
\[ \begin{align} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \label{arcpolar1} \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ. \label{arcpolar2} \end{align} \]
Find the arc length of the cardioid \(r=2+2\cos θ\).
Solution
When \(θ=0,r=2+2\cos 0 =4.\) Furthermore, as \(θ\) goes from \(0\) to \(2π\), the cardioid is traced out exactly once. Therefore these are the limits of integration. Using \(f(θ)=2+2\cos θ, α=0,\) and \(β=2π,\) Equation \ref{arcpolar1} becomes
\[\begin{align*} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{[2+2\cos θ]^2+[−2\sin θ]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4\cos^2θ+4\sin^2θ}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4(\cos^2θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{8+8\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ. \end{align*}\]
Next, using the identity \(\cos(2α)=2\cos^2α−1,\) add 1 to both sides and multiply by 2. This gives \(2+2\cos(2α)=4\cos^2α.\) Substituting \(α=θ/2\) gives \(2+2\cos θ=4\cos^2(θ/2)\), so the integral becomes
\[\begin{align*} L &= 2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{4\cos^2(\dfrac{θ}{2})}\,dθ \\[4pt] &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ.\end{align*}\]
The absolute value is necessary because the cosine is negative for some values in its domain. To resolve this issue, change the limits from \(0\) to \(π\) and double the answer. This strategy works because cosine is positive between \(0\) and \(\dfrac{π}{2}\). Thus,
\[\begin{align*} L &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ \\[4pt] &=8\int ^π_0 \cos(\dfrac{θ}{2})\,dθ \\[4pt] &=8(2\sin(\dfrac{θ}{2})∣^π_0 \\[4pt] &=16\end{align*}\]
Find the total arc length of the graph of \(r=3\sin θ\).
- Hint
-
Use Equation \ref{arcpolar1}. To determine the correct limits, make a table of values.
- Answer
-
\(s=3π\)
Key Concepts
- The area of a region in polar coordinates defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
- To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas.
- The arc length of a polar curve defined by the equation \(r=f(θ)\) with \(α≤θ≤β\) is given by the integral \(L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ\).
Key Equations
- Area of a region bounded by a polar curve \[A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ=\dfrac{1}{2}\int ^β_αr^2dθ \nonumber \]
- Arc length of a polar curve \[L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ \nonumber \]

