2.2: Solve Applications with Systems of Equations
- Page ID
- 66289
By the end of this section, you will be able to:
- Solve direct translation applications
- Solve geometry applications
- Solve uniform motion applications
Before you get started, take this readiness quiz.
- The sum of twice a number and nine is 31. Find the number.
- Twins Jon and Ron together earned $96,000 last year. Ron earned $8000 more than three times what Jon earned. How much did each of the twins earn?
- An express train and a local train leave Pittsburgh to travel to Washington, D.C. The express train can make the trip in four hours and the local train takes five hours for the trip. The speed of the express train is 12 miles per hour faster than the speed of the local train. Find the speed of both trains.
Solve Direct Translation Applications
Systems of linear equations are very useful for solving applications. Some people find setting up word problems with two variables easier than setting them up with just one variable. To solve an application, we’ll first translate the words into a system of linear equations. Then we will decide the most convenient method to use, and then solve the system.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose variables to represent those quantities.
- Translate into a system of equations.
- Solve the system of equations using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
We solved number problems with one variable earlier. Let’s see how differently it works using two variables.
Translate to a system of equations and then solve.
The sum of two numbers is zero. One number is nine less than the other. Find the numbers.
- Solution
-
Read the problem. Identify what we are looking for. We are looking for two numbers. Name what we are looking for. Let \(n= \text{the first number} \) and \(m= \text{the second number} \). Translate into a system of equations. The sum of two numbers is zero: \(\quad n+m=0.\)
One number is nine less than the other: \(\quad n=m-9.\)
The system is \(\left\{\begin{aligned} n+m&=0\\ n&=m-9\end{aligned}\right.\).
Solve the system of equations.
We will use substitution
since the second equation is solved for \(n\).\(\left\{\begin{aligned} n+m&=0\\ n&=m-9\end{aligned}\right.\)
Substitute \(m − 9\) for \(n\) in the first equation. \(\begin{aligned} n+m &=0\\ m-9+m &=0\end{aligned}\) Solve for \(m\). \(\begin{aligned}2m-9&=0\\2m&=9\\m&= \dfrac{9}{2}\end{aligned}\) Substitute \(m=\dfrac{9}{2}\) into the second equation
and then solve for \(n\).\(\begin{aligned}n&=m-9\\n&=\dfrac{9}{2}-9\\n&= \dfrac{9}{2}-\dfrac{18}{2}\\ n&=-\dfrac{9}{2}\end{aligned}\) Check the answer in the problem. \(\begin{aligned} n+m&=0 \\ -\dfrac{9}{2}+\dfrac{9}{2} & \stackrel{?}{=} 0 \\0 & \stackrel{?}{=} 0\\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} n&=m-9 \\ -\dfrac{9}{2}& \stackrel{?}{=} \dfrac{9}{2}-9 \\-\dfrac{9}{2} & \stackrel{?}{=} -\dfrac{9}{2}\\ &\quad \text{True}\end{aligned}\)
Do these numbers make sense in the problem? We will leave this to you.
Answer the question. The numbers are \(-\dfrac{9}{2}\) and \(\dfrac{9}{2}\).
Translate to a system of equations and then solve.
The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.
- Answer
-
The numbers are \(3\) and \(7\).
Translate to a system of equations and then solve.
The sum of two numbers is \(−6\). One number is 10 less than the other. Find the numbers.
- Answer
-
The numbers are \(-8\) and \(2\).
Translate to a system of equations and then solve.
Heather has been offered two options for her salary as a trainer at the gym. Option A would pay her \(\$25,000\) plus \(\$15\) for each training session. Option B would pay her \(\$10,000+\$40\) for each training session. How many training sessions would make the salary options equal?
- Solution
-
Read the problem. Identify what we are looking for. We are looking for the number of training sessions that would make the pay equal. Name what we are looking for. Let \(s= \text{ Heather’s salary}\) and \(n= \text{ the number of training sessions}\). Translate into a system of equations. Option A would pay her \(\$25,000\) plus \(\$15\) for each training session: \(\quad s=25,000+15n.\)
Option B would pay her \(\$10,000+\$40\) for each training session: \(\quad s=10,000+40n.\)
The system is \(\left\{\begin{aligned} s&=25,000+15n\\ s&=10,000+40n\end{aligned}\right.\).
Solve the system of equations.
We will use substitution since both equations are solved for \(s\).
\(\left\{\begin{aligned} s&=25,000+15n\\ s&=10,000+40n\end{aligned}\right.\)
Substitute \(25,000 +15n\) for \(s\) in the second equation. \(\begin{aligned} s&=10,000+40n \\ 25,000+15n&=10,000+40n\end{aligned}\) Solve for \(n\) \(\begin{aligned} 25,000 &= 10,000+25n \\ 15,000&=25n \\600&=n\end{aligned}\) Check the answer. Are the two options equal when \(n = 600\)?
Option A:
\(\begin{aligned} s&=25,000+15n \\ s& =25,000+15(600) \\s & = 34,000\end{aligned}\)
Option B:
\(\begin{aligned} s&=10,000+40n \\ s& =10,000+40(600) \\s & = 34,000\end{aligned}\)
Yes, the two options are equal when \(n=600\).
Are \(600\) training sessions a year reasonable? We will leave this to you.
Answer the question. The salary options would be equal for \(600\) training sessions.
Translate to a system of equations and then solve.
Geraldine has been offered positions by two insurance companies. The first company pays a salary of \(\$12,000\) plus a commission of \(\$100\) for each policy sold. The second pays a salary of \(\$20,000\) plus a commission of \(\$50\) for each policy sold. How many policies would need to be sold to make the total pay the same?
- Answer
-
To make the total pay the same \(160\) policies would need to be sold.
Translate to a system of equations and then solve.
Kenneth currently sells suits for company A at a salary of \(\$22,000\) plus a \(\$10\) commission for each suit sold. Company B offers him a position with a salary of \(\$28,000\) plus a \(\$4\) commission for each suit sold. How many suits would Kenneth need to sell for the options to be equal?
- Answer
-
\(1000\) suits would need to sell for the options to be equal.
As you solve each application, remember to analyze which method of solving the system of equations would be most convenient.
Translate to a system of equations and then solve.
When Jenna spent \(10\) minutes on the elliptical trainer and then did circuit training for \(20\) minutes, her fitness app says she burned \(278\) calories. When she spent \(20\) minutes on the elliptical trainer and \(30\) minutes circuit training she burned \(473\) calories. How many calories does she burn for each minute on the elliptical trainer? How many calories for each minute of circuit training?
- Solution
-
Read the problem. Identify what we are looking for. We are looking for the number of
calories burned each minute on the
elliptical trainer and each minute of
circuit training.Name what we are looking for. Let \(e= \text{ number of calories burned per
minute on the elliptical trainer}\) and
\(c=\text{ number of calories burned per
minute while circuit training}\).Translate into a system of equations. \(10\) minutes on the elliptical and circuit training for \(20\) minutes, burned \(278\) calories: \(\quad 10e+20c=278.\)
\(20\) minutes on the elliptical and \(30\) minutes of circuit training burned \(473\) calories: \(\quad 20e+30c=473.\)
The system is \(\left\{\begin{aligned} 10e+20c&=278\\ 20e+30c&=473\end{aligned}\right.\).
Solve the system of equations.
We will use the elimination method.
\(\left\{\begin{aligned} 10e+20c&=278\\ 20e+30c&=473\end{aligned}\right.\)
Multiply the first equation by \(−2\) to get opposite coefficients of \(e.\)
Simplify.
\(\left\{\begin{aligned}(-2)(10e+20c)&=(-2)(278)\\ 20e+30c&=473\end{aligned}\right.\)
\(\left\{\begin{aligned} -20e-40c&=-556\\ 20e+30c&=473\end{aligned}\right.\)
Add the equations. \(-10c=-83\) Solve for \(c\). \(c=8.3\) Substitute \(c = 8.3\) into one of the original equations to solve for \(e.\) \(\begin{aligned} 10e + 20 c &=278 \\ 10e + 20 (8.3)&=278 \\ 10e+166 &=278 \\ 10e&=112\\ e&=11.2\end{aligned} \)
Check the answer in the problem. \(\begin{aligned} 10e+20c&=278 \\ 10(11.2)+20(8.3) & \stackrel{?}{=} 278 \\278 & \stackrel{?}{=} 278\\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} 20e+30c&=473 \\ 20(11.2)+30(8.3) & \stackrel{?}{=} 473 \\473 & \stackrel{?}{=} 473\\ &\quad \text{True}\end{aligned}\)
Do the answer make sense? We will leave this to you.
Answer the question. Jenna burns \(8.3\) calories per minute circuit training and \(11.2\) calories per minute while on the elliptical trainer.
Translate to a system of equations and then solve.
Mark went to the gym and did \(40\) minutes of Bikram hot yoga and \(10\) minutes of jumping jacks. He burned \(510\) calories. The next time he went to the gym, he did \(30\) minutes of Bikram hot yoga and \(20\) minutes of jumping jacks burning \(470\) calories. How many calories were burned for each minute of yoga? How many calories were burned for each minute of jumping jacks?
- Answer
-
Mark burned \(11\) calories for each minute of yoga and \(7\) calories for each minute of jumping jacks.
Translate to a system of equations and then solve.
Erin spent \(30\) minutes on the rowing machine and \(20\) minutes lifting weights at the gym and burned \(430\) calories. During her next visit to the gym she spent \(50\) minutes on the rowing machine and \(10\) minutes lifting weights and burned \(600\) calories. How many calories did she burn for each minutes on the rowing machine? How many calories did she burn for each minute of weight lifting?
- Answer
-
Erin burned \(11\) calories for each minute on the rowing machine and \(5\) calories for each minute of weight lifting.
Solve Geometry Applications
We will now solve geometry applications using systems of linear equations. We will need to add complementary angles and supplementary angles to our list some properties of angles.
The measures of two complementary angles add to 90 degrees. The measures of two supplementary angles add to 180 degrees.
Two angles are complementary if the sum of the measures of their angles is 90 degrees.
Two angles are supplementary if the sum of the measures of their angles is 180 degrees.
If two angles are complementary, we say that one angle is the complement of the other.
If two angles are supplementary, we say that one angle is the supplement of the other.
Translate to a system of equations and then solve.
The difference of two complementary angles is \(26\) degrees. Find the measures of the angles.
- Solution
-
Read the problem. Identify what we are looking for. We are looking for the measure of each angle. Name what we are looking for. Let \(x=\text{ the measure of the first angle}\) and \(y= \text{ the measure of the second angle}\). Translate into a system of equations. The angles are complementary: \(\quad x+y=90.\)
The difference of the two angles is \(26\) degrees: \(\quad x−y=26.\)
The system is \(\left\{ \begin{array} {l} x+y=90 \\ x−y=26 \end{array} \right..\)
Solve the system of equations.
We will use the elimination method.
\(\left\{ \begin{array} {l} x+y=90 \\ x−y=26 \end{array} \right. \)
Add the equations and solve for \(x.\) \(\begin{aligned} 2x&=116 \\x&=58\end{aligned}\) Substitute \(x=58\) into the first equation. \(\begin{aligned}x+y&=90\\58+y&=90\\y&=32\end{aligned}\) Check the answer in the problem. \(\begin{aligned} x+y&=90 \\ 58+32 & \stackrel{?}{=} 90 \\90 & \stackrel{?}{=} 90\\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} x-y&=26 \\ 58-32 & \stackrel{?}{=} 26 \\26 & \stackrel{?}{=} 26\\ &\quad \text{True}\end{aligned}\)
Does the answer make sense? We will leave this to you.
Answer the question. The angle measures are \(32\) and \(58\) degrees.
Translate to a system of equations and then solve.
The difference of two complementary angles is \(20\) degrees. Find the measures of the angles.
- Answer
-
The angle measures are \(35\) and \(55\) degrees.
Translate to a system of equations and then solve.
The difference of two complementary angles is \(80\) degrees. Find the measures of the angles.
- Answer
-
The angle measures are \(5\) and \(85\) degrees.
In the next example, we remember that the measures of supplementary angles add to \(180\).
Translate to a system of equations and then solve.
Two angles are supplementary. The measure of the larger angle is twelve degrees less than five times the measure of the smaller angle. Find the measures of both angles.
- Solution
-
Read the problem. Identify what we are looking for. We are looking for measure of each angle. Name what we are looking for. Let \(x=\text{ the measure of the first angle}\) and \(y=\text{ the measure of the second angle}\). Translate into a system of equations. The angles are supplementary: \(\quad x+y=180.\)
The larger angle is twelve less than five
times the smaller angle: \(\quad y=5x-12.\)The system is \(\left\{ \begin{array} {l} x+y=180 \\ y=5x-12 \end{array} \right..\)
Solve the system of equations.
We will use substitution since the second equation is solved for \(y\).
\(\left\{ \begin{aligned} x+y&=180 \\ y&=5x-12 \end{aligned} \right. \)
Substitute \(5x − 12\) for \(y\) in the first equation. \(\begin{aligned} x+y&=180 \\ x+(5x-12)&=180\end{aligned}\) Solve for \(x\). \(\begin{aligned} 6x-12& =180\\6x&=192\\x&=32\end{aligned}\) Substitute \(32\) for \(x\) in the second equation, then solve for \(y\). \(\begin{aligned} y&=5x-12 \\ y&=5(32)-12 \\ y&= 160-12 \\ y&=148\end{aligned}\) Check the answer in the problem. \(\begin{aligned} x+y&=180 \\ 32+148 & \stackrel{?}{=} 180 \\180 & \stackrel{?}{=}180 \\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} y&=5x-12 \\ 148 & \stackrel{?}{=} 5(32)-12 \\148 & \stackrel{?}{=}148 \\ &\quad \text{True}\end{aligned}\)
Does the answer make sense? We will leave this to you.
Answer the question. The angle measures are \(32\) and \(148\) degrees.
Translate to a system of equations and then solve.
Two angles are supplementary. The measure of the larger angle is \(12\) degrees more than three times the smaller angle. Find the measures of the angles.
- Answer
-
The angle measures are \(42\) and \(138\) degrees.
Translate to a system of equations and then solve.
Two angles are supplementary. The measure of the larger angle is \(18\) less than twice the measure of the smaller angle. Find the measures of the angles.
- Answer
-
The angle measures are \(66\) and \(114\) degrees.
Recall that the angles of a triangle add up to \(180\) degrees. A right triangle has one angle that is \(90\) degrees. What does that tell us about the other two angles? In the next example we will be finding the measures of the other two angles.
Translate to a system of equations and then solve.
The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle. Find the measures of both angles.
- Solution
-
We will draw and label a figure.
Read the problem. Identify what you are looking for. We are looking for the measures of the angles. Name what we are looking for. Let \(a=\text{the measure of the first angle}\) and
\(b=\text{the measure of the second angle}\). Note that we don't have to name our unknowns \(x\) and \(y\), but can pick letters we like.
Translate into a system of equations. The measure of one of the small angles of a right triangle is ten more than three times the measure of the other small angle: \(\quad a = 3b+10.\)
The sum of the measures of the angles of a triangle is \(180\): \(\quad a + b+90=180.\)
The system is \(\left\{\begin{aligned}a &= 3b+10 \\a + b+90&=180\end{aligned}\right..\)
Solve the system of equations.
We will use substitution since the first equation is solved for \(a.\)
\(\left\{\begin{aligned}a &= 3b+10 \\a + b+90&=180\end{aligned}\right.\)
Substitute \(3b+10\) for \(a\) in the second equation. \(\begin{aligned} a + b+90&=180 \\ (3b+10)+b+90& = 180\end{aligned}\) Solve for \(b\). \(\begin{aligned}4 b+100&=180 \\ 4b &=80 \\b&=20\end{aligned}\) Substitute \(b=20\) into the first equation and then solve for \(a\). \(\begin{aligned}a&=3b+10 \\ a&=3(20)+10 \\a&=70\end{aligned}\) Check the answer in the problem. \(\begin{aligned} a &= 3b+10 \\ 70 & \stackrel{?}{=} 3(20)+10 \\70 & \stackrel{?}{=}70 \\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} a + b+90&=180 \\ 70+ 20+90 & \stackrel{?}{=} 180 \\180 & \stackrel{?}{=}180 \\ &\quad \text{True}\end{aligned}\)
Does the answer make sense? We will leave this to you.
Answer the question. The measures of the small angles are \(20\) and \(70\) degrees.
Translate to a system of equations and then solve.
The measure of one of the small angles of a right triangle is \(2\) more than \(3\) times the measure of the other small angle. Find the measure of both angles.
- Answer
-
The angle measures are \(22\) and \(68\) degrees.
Translate to a system of equations and then solve.
The measure of one of the small angles of a right triangle is \(18\) less than twice the measure of the other small angle. Find the measure of both angles.
- Answer
-
The angle measures are \(36\) and \(54\) degrees.
Often it is helpful when solving geometry applications to draw a picture to visualize the situation.
Translate to a system of equations and then solve.
Randall has \(125\) feet of fencing to enclose the part of his backyard adjacent to his house. He will only need to fence around three sides, because the fourth side will be the wall of the house. He wants the length of the fenced yard (parallel to the house wall) to be \(5\) feet more than four times as long as the width. Find the length and the width.
- Solution
-
Read the problem. Identify what you are looking for. We are looking for the length and width.
Name what we are looking for. Let \(L=\text{ the length of the fenced yard}\) and
\(W=\text{ the width of the fenced yard.}\) Here we choose letters that will help remind us of their meaning.Translate into a system of equations. One length and two widths equal \(125\): \(\quad L + 2W = 125.\)
The length will be \(5\) feet more than four times the width: \(\quad L = 4W +5.\)
The system is \(\left\{\begin{aligned}L + 2W &= 125 \\L &= 4W +5 \end{aligned}\right..\)
Solve the system.
We will use substitution since the second equation is solved for \(L.\)
\(\left\{\begin{aligned}L + 2W &= 125 \\L &= 4W +5 \end{aligned}\right.\)
Substitute \(L = 4W + 5\) into the first
equation.\(\begin{aligned}L + 2W &= 125 \\(4W +5) +2W &= 125 \end{aligned}\)
Solve for \(W\). \(\begin{aligned}6W+5 &= 125 \\ 6W &=120 \\W&=20 \end{aligned}\)
Substitute \(20\) for \(W\) in the second
equation, then solve for \(L\).\(\begin{aligned} L &= 4W +5\\L &= 4(20) +5 \\ L&=85\end{aligned}\) Check the answer in the problem. \(\begin{aligned} L + 2W &= 125 \\ 85 + 2(20) & \stackrel{?}{=} 125 \\125 & \stackrel{?}{=}125 \\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} L &= 4W +5 \\ 85 & \stackrel{?}{=} 4(20)+5 \\85 & \stackrel{?}{=}85 \\ &\quad \text{True}\end{aligned}\)
Does the answer make sense? We will leave this to you.
Answer the question. The length is \(85\) feet and the width is \(20\) feet.
Translate to a system of equations and then solve.
Mario wants to put a fence around the pool in his backyard. Since one side is adjacent to the house, he will only need to fence three sides. There are two long sides and the one shorter side is parallel to the house. He needs \(155\) feet of fencing to enclose the pool. The length of the long side is \(10\) feet less than twice the width. Find the length and width of the pool area to be enclosed.
- Answer
-
The length is \(60\) feet and the width is \(35\) feet.
Translate to a system of equations and then solve.
Alexis wants to build a rectangular dog run in her yard adjacent to her neighbor’s fence. She will use \(136\) feet of fencing to completely enclose the rectangular dog run. The length of the dog run along the neighbor’s fence will be \(16\) feet less than twice the width. Find the length and width of the dog run.
- Answer
-
The length is \(60\) feet and the width is \(38\) feet.
Solve Uniform Motion Applications
We used a table to organize the information in uniform motion problems when we introduced them earlier. We will continue using the table here. The basic equation was \(D=rt\) where \(D\) is the distance traveled, \(r\) is the rate, and \(t\) is the time.
Our first example of a uniform motion application will be for a situation similar to some we have already seen, but now we can use two variables and two equations.
Translate to a system of equations and then solve.
Joni left St. Louis on the interstate, driving west towards Denver at a speed of \(65\) miles per hour. Half an hour later, Kelly left St. Louis on the same route as Joni, driving \(78\) miles per hour. How long will it take Kelly to catch up to Joni?
- Solution
-
Read the problem. A diagram is useful in helping us visualize the situation.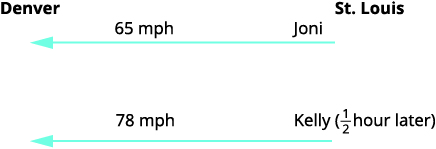 
Identify what we are looking for.
We are looking for the length of time Kelly and Joni will each drive. Name what we are looking for. Let \(k=\text{ the length of time Kelly will drive }\) and \(j=\text{ the length of time Joni will drive. }\) A chart will help us organize the data. We know the rates of both Joni and Kelly, and so we enter them in the chart.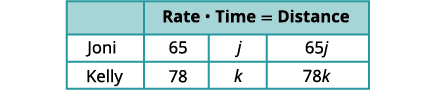 
Since \(\text{Distance}=\text{rate} \cdot \text{time}\), we can fill in the Distance column.
Translate into a system of equations. To make the system of equations, we must recognize that Kelly and Joni will drive the same distance: \(\quad 65j=78k.\)
Also, since Kelly left later, her time will be \(\dfrac{1}{2}\) hour less than Joni’s time: \(\quad k=j-\dfrac{1}{2}.\)
The system is \(\left\{ \begin{array} {l} k=j−\dfrac{1}{2} \\ 65j=78k \end{array} \right..\)
Solve the system.
We will use substitution since the first equation is solved for \(k\).
\(\left\{ \begin{aligned} k&=j−\dfrac{1}{2} \\ 65j&=78k \end{aligned} \right.\)
Substitute \(k=j−\dfrac{1}{2}\) into the second equation. \(\left\{ \begin{aligned} 65j&=78k \\ 65j &= 78\left(j−\dfrac{1}{2}\right) \end{aligned} \right.\) Solve for \(j\). \(\left\{ \begin{aligned} 65j&=78j−39 \\ −13j&=−39 \\ j &=3 \end{aligned} \right.\) To find Kelly’s time, substitute \(j=3\) into the first equation, then solve for \(k.\) \(\begin{aligned} k &=j−\dfrac{1}{2} \\ k &=3−\dfrac{1}{2} \\k&=\dfrac{5}{2} \\ k&=2\dfrac{1}{2}\end{aligned}\) Check the answer in the problem. \(\begin{aligned} k&=j−\dfrac{1}{2} \\ 2\dfrac{1}{2}& \stackrel{?}{=}3-\dfrac{1}{2} \\2\dfrac{1}{2} & \stackrel{?}{=} 2\dfrac{1}{2}\\ &\quad \text{True}\end{aligned}\)
\(\begin{aligned} 65j&=78k \\ 65(3) & \stackrel{?}{=} 78 \left(\dfrac{5}{2}\right)\\195 & \stackrel{?}{=} 195\\ &\quad \text{True}\end{aligned}\)
They will have traveled the same distance, \(195\) miles, when they meet.
Does the answer make sense? We will leave this to you.
Answer the question. Kelly will catch up to Joni in \(2\dfrac{1}{2}\) hours. By then, Joni will have traveled \(3\) hours.
Translate to a system of equations and then solve.
Mitchell left Detroit on the interstate driving south towards Orlando at a speed of \(60\) miles per hour. Clark left Detroit \(1\) hour later traveling at a speed of \(75\) miles per hour, following the same route as Mitchell. How long will it take Clark to catch Mitchell?
- Answer
-
It will take Clark \(4\) hours to catch Mitchell.
Translate to a system of equations and then solve.
Charlie left his mother’s house traveling at an average speed of \(36\) miles per hour. His sister Sally left \(15\) minutes \(\left(\dfrac{1}{4} \text{ hour}\right)\) later traveling the same route at an average speed of \(42\) miles per hour. How long before Sally catches up to Charlie?
- Answer
-
It will take Sally \(112\) hours to catch up to Charlie.
Many real-world applications of uniform motion arise because of the effects of currents—of water or air—on the actual speed of a vehicle. Cross-country airplane flights in the United States generally take longer going west than going east because of the prevailing wind currents.
Let’s take a look at a boat traveling on a river. Depending on which way the boat is going, the current of the water is either slowing it down or speeding it up.
The images below show how a river current affects the speed at which a boat is actually traveling. We will call the speed of the boat in still water \(b\) and the speed of the river current \(c\).
The boat is going downstream, in the same direction as the river current. The current helps push the boat, so the boat’s actual speed is faster than its speed in still water. The actual speed at which the boat is moving is \(b+c\).
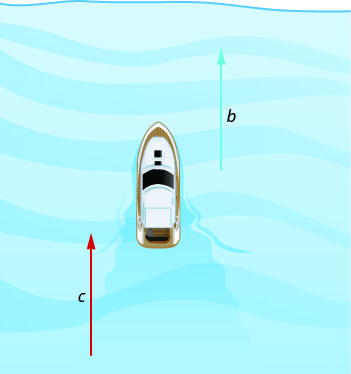
Now, the boat is going upstream, opposite to the river current. The current is going against the boat, so the boat’s actual speed is slower than its speed in still water. The actual speed of the boat is \(b−c\).
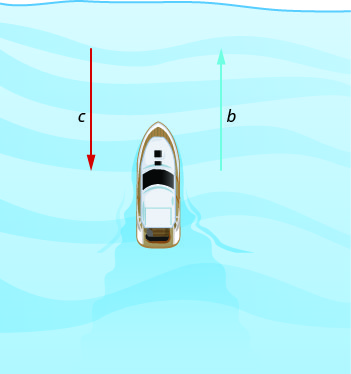
We will put some numbers to this situation in the next example.
Translate to a system of equations and then solve.
A river cruise ship sailed \(60\) miles downstream for \(4\) hours and then took \(5\) hours sailing upstream to return to the dock. Find the speed of the ship in still water and the speed of the river current.
- Solution
-
Read the problem. This is a uniform motion problem and a
picture will help us visualize the situation.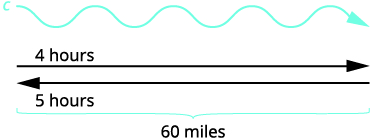
Identify what we are looking for. We are looking for the speed of the ship in still water and the speed of the current. Name what we are looking for. Let \(s= \text{the rate of the ship in still water}\) and \(c= \text{the rate of the current}\). A chart will help us organize the information.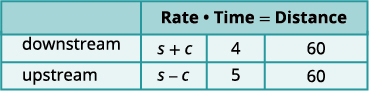 
\(\text{Distance}=\text{rate} \cdot \text{time}\)
Translate into a system of equations. The ship goes downstream and then upstream.
Going downstream, the current helps the
ship and so the ship's actual rate is \(s + c\).Going upstream, the current slows the ship
and so the actual rate is \(s − c\).Downstream it takes \(4\) hours. Upstream it takes \(5\) hours.
Each way the distance is \(60\) miles.
The system is \(\left\{ \begin{array} {l} 4(s+c)=60 \\ 5(s-c)=60 \end{array} \right..\)
Solve the system of equations.
Distribute to put both equations in standard
form, then solve by elimination.\(\left\{ \begin{aligned} 4(s+c)&=60 \\ 5(s-c)&=60 \end{aligned} \right.\)
\(\left\{\begin{aligned} 4s+4c&=60 \\ 5s-5c&=60 \end{aligned} \right.\)
Multiply the top equation by \(5\) and the
bottom equation by \(4\).\(\left\{\begin{aligned} 5(4s+4c)&=5(60) \\ 4(5s-5c)&=4(60) \end{aligned} \right.\)
\(\left\{\begin{aligned} 20s+20c&=300 \\ 20s-20c&=240 \end{aligned} \right.\)
Add the equations, then solve for \(s\). \(\begin{aligned} 40s &= 540 \\ s&= 13.5\end{aligned}\) Substitute \(s = 13.5\) into of the original
equations.\(\begin{aligned} 4(s+c)&=60 \\ 4(13.5+c)&=60 \\ 54 + 4c &= 60 \\ 4c&=6 \\ c&=1.5\end{aligned}\)
Check the answer in the problem. \(\begin{aligned} 4(s+c)&=60 \\ 4(13.5+1.5)& \stackrel{?}{=}60 \\60 & \stackrel{?}{=} 60\\ &\quad \text{True}\end{aligned}\)
The downstream rate would be \(13.5+1.5=15\) mph. In 4 hours the ship would travel \(15\cdot 4=60\) miles.
\(\begin{aligned} 5(s-c)&=60 \\ 5(13.5-1.5)& \stackrel{?}{=}60 \\60 & \stackrel{?}{=} 60\\ &\quad \text{True}\end{aligned}\)
The upstream rate would be \(13.5−1.5=12\) mph. In 5 hours the ship would travel \(12\cdot 5=60\) miles.
Does the answer make sense? We will leave this to you.
Answer the question. The rate of the ship is \(13.5\) mph and the rate of the current is \(1.5\) mph.
Translate to a system of equations and then solve.
A Mississippi river boat cruise sailed 120 miles upstream for 12 hours and then took 10 hours to return to the dock. Find the speed of the river boat in still water and the speed of the river current.
- Answer
-
The rate of the boat is 11 mph and the rate of the current is 1 mph.
Translate to a system of equations and then solve.
Jason paddled his canoe \(24\) miles upstream for \(4\) hours. It took him \(3\) hours to paddle back. Find the speed of the canoe in still water and the speed of the river current.
- Answer
-
The speed of the canoe is \(7\) mph and the speed of the current is \(1\) mph.
Wind currents affect airplane speeds in the same way as water currents affect boat speeds. We will see this in the next example. A wind current in the same direction as the plane is flying is called a tailwind. A wind current blowing against the direction of the plane is called a headwind.
Translate to a system of equations and then solve.
A private jet can fly \(1,095\) miles in three hours with a tailwind but only \(987\) miles in three hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Solution
-
Read the problem. This is a uniform motion problem and a picture will help us visualize.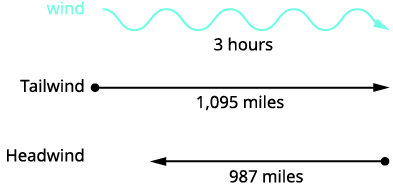 
Identify what we are looking for. We are looking for the speed of the jet in still air and the speed of the wind. Name what we are looking for. Let \(j=\text{ the speed of the jet in still air}\) and \(w=\text{ the speed of the wind}\). A chart will help us organize the information.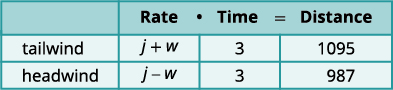 
\(\text{Distance}=\text{Rate} \cdot \text{Time}\)
Translate into a system of equations. The jet makes two trips—one in a tailwind
and one in a headwind.In a tailwind, the wind helps the jet and so
the rate is \(j + w\).In a headwind, the wind slows the jet and
so the rate is \(j ‒ w\).Each trip takes \(3\) hours. In a tailwind the jet flies \(1,095\) miles. In a headwind the jet flies \(987\) miles.
The system is \(\left\{ \begin{array} {l} 3(j+w)=1095 \\ 3(j-w)=987 \end{array} \right..\)
Solve the system of equations.
Distribute, then solve by elimination.
\(\left\{ \begin{aligned} 3(j+w)&=1095 \\ 3(j-w)&=987 \end{aligned} \right.\)
\(\left\{ \begin{aligned} 3j+3w&=1095 \\ 3j-3w&=987 \end{aligned} \right.\)
Add and solve for \(j\). \(\begin{aligned} 6j&=2082 \\ j&= 347\end{aligned}\) Substitute \(j = 347\) into one of the original
equations,\(\begin{aligned} 3(j+w)&=1095\\ 3(347+w)&=1095\end{aligned}\)
Solve for \(w\). \(\begin{aligned} 1041 +3w&=1095\\ 3w&=54 \\ w&=18\end{aligned}\) Check the answer in the problem. \(\begin{aligned} 3(j+w)&=1095 \\ 3(347+ 18)& \stackrel{?}{=}1095 \\1095 & \stackrel{?}{=} 1095\\ &\quad \text{True}\end{aligned}\)
With the tailwind, the actual rate of the
jet would be \(347+18=365\) mph. In \(3\) hours the jet would travel \(365\cdot 3=1,095\) miles\(\begin{aligned} 3(j-w)&=987 \\ 3(347-18) & \stackrel{?}{=} 987 \\987& \stackrel{?}{=} 987\\ &\quad \text{True}\end{aligned}\)
Going into the headwind, the jet’s actual
rate would be \(347−18=329\) mph. In \(3\) hours the jet would travel \(329\cdot 3=987\) miles.Does the answer make sense? We will leave this to you.
Answer the question. The rate of the jet is \(347\) mph and the rate of the wind is \(18\) mph.
Translate to a system of equations and then solve.
A small jet can fly \(1,325\) miles in \(5\) hours with a tailwind but only \(1,035\) miles in \(5\) hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
The speed of the jet is \(235\) mph and the speed of the wind is \(30\) mph.
Translate to a system of equations and then solve.
A commercial jet can fly \(1,728\) miles in \(4\) hours with a tailwind but only \(1,536\) miles in \(4\) hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
The speed of the jet is \(408\) mph and the speed of the wind is \(24\) mph.
Key Concepts
- How To Solve Applications with Systems of Equations
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose variables to represent those quantities.
- Translate into a system of equations.
- Solve the system of equations using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Glossary
- complementary angles
- Two angles are complementary if the sum of the measures of their angles is 90 degrees.
- supplementary angles
- Two angles are supplementary if the sum of the measures of their angles is 180 degrees.
Practice Makes Perfect
Direct Translation Applications
In the following exercises, translate to a system of equations and solve.
1. The sum of two number is 15. One number is 3 less than the other. Find the numbers.
2. The sum of two number is 30. One number is 4 less than the other. Find the numbers.
- Answer
-
13 and 17
3. The sum of two number is −16. One number is 20 less than the other. Find the numbers.
4. The sum of two number is \(−26\). One number is 12 less than the other. Find the numbers.
- Answer
-
\(−7\) and \(−19\)
5. The sum of two numbers is 65. Their difference is 25. Find the numbers.
6. The sum of two numbers is 37. Their difference is 9. Find the numbers.
- Answer
-
\(14\) and \(23\)
7. The sum of two numbers is \(−27\). Their difference is \(−59\). Find the numbers.
8. The sum of two numbers is \(−45\). Their difference is \(−89\). Find the numbers.
- Answer
-
\(22\) and \(−67\)
9. Maxim has been offered positions by two car companies. The first company pays a salary of $10,000 plus a commission of $1000 for each car sold. The second pays a salary of $20,000 plus a commission of $500 for each car sold. How many cars would need to be sold to make the total pay the same?
10. Jackie has been offered positions by two cable companies. The first company pays a salary of $14,000 plus a commission of $100 for each cable package sold. The second pays a salary of $20,000 plus a commission of $25 for each cable package sold. How many cable packages would need to be sold to make the total pay the same?
- Answer
-
Eighty cable packages would need to be sold to make the total pay the same.
11. Amara currently sells televisions for company A at a salary of $17,000 plus a $100 commission for each television she sells. Company B offers her a position with a salary of $29,000 plus a $20 commission for each television she sells. How televisions would Amara need to sell for the options to be equal?
12. Mitchell currently sells stoves for company A at a salary of $12,000 plus a $150 commission for each stove he sells. Company B offers him a position with a salary of $24,000 plus a $50 commission for each stove he sells. How many stoves would Mitchell need to sell for the options to be equal?
- Answer
-
Mitchell would need to sell 120 stoves for the companies to be equal.
13. Two containers of gasoline hold a total of fifty gallons. The big container can hold ten gallons less than twice the small container. How many gallons does each container hold?
14. June needs 48 gallons of punch for a party and has two different coolers to carry it in. The bigger cooler is five times as large as the smaller cooler. How many gallons can each cooler hold?
- Answer
-
8 and 40 gallons
15. Shelly spent 10 minutes jogging and 20 minutes cycling and burned 300 calories. The next day, Shelly swapped times, doing 20 minutes of jogging and 10 minutes of cycling and burned the same number of calories. How many calories were burned for each minute of jogging and how many for each minute of cycling?
16. Drew burned 1800 calories Friday playing one hour of basketball and canoeing for two hours. Saturday he spent two hours playing basketball and three hours canoeing and burned 3200 calories. How many calories did he burn per hour when playing basketball? How many calories did he burn per hour when canoeing?
- Answer
-
1000 calories playing basketball and 400 calories canoeing
17. Troy and Lisa were shopping for school supplies. Each purchased different quantities of the same notebook and thumb drive. Troy bought four notebooks and five thumb drives for $116. Lisa bought two notebooks and three thumb dives for $68. Find the cost of each notebook and each thumb drive.
18. Nancy bought seven pounds of oranges and three pounds of bananas for $17. Her husband later bought three pounds of oranges and six pounds of bananas for $12. What was the cost per pound of the oranges and the bananas?
- Answer
-
Oranges cost $2 per pound and bananas cost $1 per pound
19. Andrea is buying some new shirts and sweaters. She is able to buy 3 shirts and 2 sweaters for $114 or she is able to buy 2 shirts and 4 sweaters for $164. How much does a shirt cost? How much does a sweater cost?
20. Peter is buying office supplies. He is able to buy 3 packages of paper and 4 staplers for $40 or he is able to buy 5 packages of paper and 6 staplers for $62. How much does a package of paper cost? How much does a stapler cost?
- Answer
-
Package of paper $4, stapler $7
21. The total amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot dog? How much sodium is in a cup of cottage cheese?
22. The total number of calories in 2 hot dogs and 3 cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot dog? How many calories are in a cup of cottage cheese?
- Answer
-
Hot dog 150 calories, cup of cottage cheese 220 calories
23. Molly is making strawberry infused water. For each ounce of strawberry juice, she uses three times as many ounces of water as juice. How many ounces of strawberry juice and how many ounces of water does she need to make 64 ounces of strawberry infused water?
24. Owen is making lemonade from concentrate. The number of quarts of water he needs is 4 times the number of quarts of concentrate. How many quarts of water and how many quarts of concentrate does Owen need to make 100 quarts of lemonade?
- Answer
-
Owen will need 80 quarts of water and 20 quarts of concentrate to make 100 quarts of lemonade.
Solve Geometry Applications
In the following exercises, translate to a system of equations and solve.
25. The difference of two complementary angles is 55 degrees. Find the measures of the angles.
26. The difference of two complementary angles is 17 degrees. Find the measures of the angles.
- Answer
-
\(53.5\) degrees and \(36.5\) degree.
27. Two angles are complementary. The measure of the larger angle is twelve less than twice the measure of the smaller angle. Find the measures of both angles.
28. Two angles are complementary. The measure of the larger angle is ten more than four times the measure of the smaller angle. Find the measures of both angles.
- Answer
-
16 degrees and 74 degrees
29. The difference of two supplementary angles is 8 degrees. Find the measures of the angles.
30. The difference of two supplementary angles is 88 degrees. Find the measures of the angles.
- Answer
-
134 degrees and 46 degrees
31. Two angles are supplementary. The measure of the larger angle is four more than three times the measure of the smaller angle. Find the measures of both angles.
32. Two angles are supplementary. The measure of the larger angle is five less than four times the measure of the smaller angle. Find the measures of both angles.
- Answer
-
37 degrees and 143 degrees
33. The measure of one of the small angles of a right triangle is 14 more than 3 times the measure of the other small angle. Find the measure of both angles.
34. The measure of one of the small angles of a right triangle is 26 more than 3 times the measure of the other small angle. Find the measure of both angles.
- Answer
-
\(16°\) and \(74°\)
35. The measure of one of the small angles of a right triangle is 15 less than twice the measure of the other small angle. Find the measure of both angles.
36. The measure of one of the small angles of a right triangle is 45 less than twice the measure of the other small angle. Find the measure of both angles.
- Answer
-
\(45°\) and \(45°\)
37. Wayne is hanging a string of lights 45 feet long around the three sides of his patio, which is adjacent to his house. The length of his patio, the side along the house, is five feet longer than twice its width. Find the length and width of the patio.
38. Darrin is hanging 200 feet of Christmas garland on the three sides of fencing that enclose his front yard. The length is five feet less than three times the width. Find the length and width of the fencing.
- Answer
-
Width is 41 feet and length is 118 feet.
39. A frame around a family portrait has a perimeter of 90 inches. The length is fifteen less than twice the width. Find the length and width of the frame.
40. The perimeter of a toddler play area is 100 feet. The length is ten more than three times the width. Find the length and width of the play area.
- Answer
-
Width is 10 feet and length is 40 feet.
Solve Uniform Motion Applications
In the following exercises, translate to a system of equations and solve.
41. Sarah left Minneapolis heading east on the interstate at a speed of 60 mph. Her sister followed her on the same route, leaving two hours later and driving at a rate of 70 mph. How long will it take for Sarah’s sister to catch up to Sarah?
42. College roommates John and David were driving home to the same town for the holidays. John drove 55 mph, and David, who left an hour later, drove 60 mph. How long will it take for David to catch up to John?
- Answer
-
11 hours
43. At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 40 mph. Lucy’s friend left the beach for home 30 minutes (half an hour) later, and drove 50 mph. How long did it take Lucy’s friend to catch up to Lucy?
44. Felecia left her home to visit her daughter driving 45 mph. Her husband waited for the dog sitter to arrive and left home twenty minutes (1/3 hour) later. He drove 55 mph to catch up to Felecia. How long before he reaches her?
- Answer
-
\(1.5\) hour
45. The Jones family took a 12-mile canoe ride down the Indian River in two hours. After lunch, the return trip back up the river took three hours. Find the rate of the canoe in still water and the rate of the current.
46. A motor boat travels 60 miles down a river in three hours but takes five hours to return upstream. Find the rate of the boat in still water and the rate of the current.
- Answer
-
Boat rate is 16 mph and current rate is 4 mph.
47. A motor boat traveled 18 miles down a river in two hours but going back upstream, it took 4.54.5 hours due to the current. Find the rate of the motor boat in still water and the rate of the current. (Round to the nearest hundredth.)
48. A river cruise boat sailed 80 miles down the Mississippi River for four hours. It took five hours to return. Find the rate of the cruise boat in still water and the rate of the current.
- Answer
-
Boat rate is 18 mph and current rate is 2 mph.
49. A small jet can fly 1072 miles in 4 hours with a tailwind but only 848 miles in 4 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
50. A small jet can fly 1435 miles in 5 hours with a tailwind but only 1,215 miles in 5 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
Jet rate is 265 mph and wind speed is 22 mph.
51. A commercial jet can fly 868 miles in 2 hours with a tailwind but only 792 miles in 2 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
52. A commercial jet can fly 1,320 miles in 3 hours with a tailwind but only 1170 miles in 3 hours into a headwind. Find the speed of the jet in still air and the speed of the wind.
- Answer
-
Jet rate is 415 mph and wind speed is 25 mph.
Writing Exercises
53. Write an application problem similar to Example 2.2.4. Then translate to a system of equations and solve it.\
54. Write a uniform motion problem similar to Example 2.2.23 that relates to where you live with your friends or family members. Then translate to a system of equations and solve it.
- Answer
-
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?