3.5: Rational Functions
- Page ID
- 239
1. Rational Functions (Definition)
is a quotient of polynomials \(\dfrac{P(x)}{Q(x)}\).
are all Rational Functions
\[\{x | x \text{ is not }1 \text{ or } -1\}.\]
2. Vertical Asymptotes
of a rational function occurs where the denominator is 0.
\[f(x) \rightarrow\infty.\]
Four Types of Vertical Asymptotes
Below are the four types of vertical asymptotes:
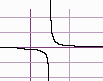
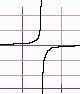
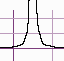
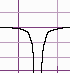
3. Horizontal Asymptotes
and we have the the left and right behavior of the graph is a horizontal line \(y = 3\).
4. Oblique Asymptotes
Consider the function
\[f(x) = \dfrac{(x^2 - 3x - 4)}{(x + 3)}\]
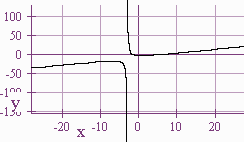
\(f(x)\) does not have a horizontal asymptote, since
\[\dfrac{x^2}{x}= x \]
is not a constant, but we see (on the calculator) that the left and right behavior of the curve is like a line. Our goal is to find the equation of this line.
We use synthetic division to see that
\[\dfrac{(x^2 - 3x - 4)}{(x + 3)} = x - 6 + \dfrac{14}{(x+3)}.\]
For very large \(x\),
\[\dfrac{14}{x} + 3\]
is very small, hence \(f(x)\) is approximately equal to
\[x - 6\]
on the far left and far right of the graph. We call this line an Oblique Asymptote.
To graph, we see that there is a vertical asymptote at
\[x = -3\]
with behavior:
left down and right up
The graph has x-intercepts at 4 and -1, and a y intercept at \(-\frac{4}{3}\).
\[\dfrac{(x^3 + 8)}{(x^2 - 3x - 4)}\]
5. Rational Functions With Common Factors
Consider the graph of
\[y = \dfrac{x-1}{x-1}\]
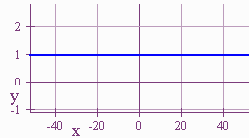
What is wrong with the picture? When
\[f(x) = \dfrac{g(x)(x - r)}{h(x)(x - r)}\]
with neither \(g(r)\) nor \(h(r)\) zero, the graph will have a hole at \(x = r\). We call this hole a removable discontinuity.
at \((2,2)\).
We end our discussion with a list of steps for graphing rational functions.
Steps in graphing rational functions:
- Step 1 Plug in \(x = 0\) to find the y-intercept
- Step 2 Factor the numerator and denominator. Cancel any common factors remember to put in the appropriate holes if necessary.
- Step 3 Set the numerator = 0 to find the x-intercepts
- Step 4 Set the denominator = 0 to find the vertical asymptotes. Then plug in nearby values to fine the left and right behavior of the vertical asymptotes.
- Step 5 If the degree of the numerator = degree of the denominator then the graph has a horizontal asymptote. To determine the value of the horizontal asymptote, divide the term highest power of the numerator by the term of highest power of the denominator.
- If the degree of the numerator = degree of the denominator + 1, then use polynomial or synthetic division to determine the equation of the oblique asymptote.
- Step 6 Graph it!
Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


