1.6: Properties of Real Numbers
- Page ID
- 5121
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Use the commutative and associative properties
- Use the properties of identity, inverse, and zero
- Simplify expressions using the Distributive Property
Use the Commutative and Associative Properties
The order we add two numbers doesn’t affect the result. If we add \(8+9\) or \(9+8\), the results are the same—they both equal 17. So, \(8+9=9+8\). The order in which we add does not matter!
Similarly, when multiplying two numbers, the order does not affect the result. If we multiply \(9·8\) or \(8·9\) the results are the same—they both equal 72. So, \(9·8=8·9\). The order in which we multiply does not matter! These examples illustrate the Commutative Property.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \]
When adding or multiplying, changing the order gives the same result.
The Commutative Property has to do with order. We subtract \(9−8\) and \(8−9\), and see that \(9−8\neq 8−9\). Since changing the order of the subtraction does not give the same result, we know that subtraction is not commutative.
Division is not commutative either. Since \(12÷3\neq 3÷12\), changing the order of the division did not give the same result. The commutative properties apply only to addition and multiplication!
- Addition and multiplication are commutative.
- Subtraction and division are not commutative.
When adding three numbers, changing the grouping of the numbers gives the same result. For example,\((7+8)+2=7+(8+2)\), since each side of the equation equals 17.
This is true for multiplication, too. For example, \(\left(5·\frac{1}{3}\right)·3=5·\left(\frac{1}{3}·3\right)\), since each side of the equation equals 5.
These examples illustrate the Associative Property.
\[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \]
When adding or multiplying, changing the grouping gives the same result.
The Associative Property has to do with grouping. If we change how the numbers are grouped, the result will be the same. Notice it is the same three numbers in the same order—the only difference is the grouping.
We saw that subtraction and division were not commutative. They are not associative either.
\[\begin{array}{cc} (10−3)−2\neq 10−(3−2) & (24÷4)÷2\neq 24÷(4÷2) \\ 7−2\neq 10−1 & 6÷2\neq 24÷2 \\ 5\neq 9 & 3\neq 12 \end{array}\]
When simplifying an expression, it is always a good idea to plan what the steps will be. In order to combine like terms in the next example, we will use the Commutative Property of addition to write the like terms together.
Simplify: \(18p+6q+15p+5q\).
- Answer
-
\[\begin{array}{lc} \text{} & 18p+6q+15p+5q \\ \text{Use the Commutative Property of addition to} & 18p+15p+6q+5q \\ \text{reorder so that like terms are together.} & {} \\ \text{Add like terms.} & 33p+11q \end{array}\]
Simplify: \(23r+14s+9r+15s\).
- Answer
-
\(32r+29s\)
Simplify: \(37m+21n+4m−15n\).
- Answer
-
\(41m+6n\)
When we have to simplify algebraic expressions, we can often make the work easier by applying the Commutative Property or Associative Property first.
Simplify: \((\frac{5}{13}+\frac{3}{4})+\frac{1}{4}\).
- Answer
-
\( \begin{array}{lc} \text{} & (\frac{5}{13}+\frac{3}{4})+\frac{1}{4} \\ {\text{Notice that the last 2 terms have a common} \\ \text{denominator, so change the grouping.} } & \frac{5}{13}+(\frac{3}{4}+\frac{1}{4}) \\ \text{Add in parentheses first.} & \frac{5}{13}+(\frac{4}{4}) \\ \text{Simplify the fraction.} & \frac{5}{13}+1 \\ \text{Add.} & 1\frac{5}{13} \\ \text{Convert to an improper fraction.} & \frac{18}{13} \end{array}\)
Simplify: \((\frac{7}{15}+\frac{5}{8})+\frac{3}{8}.\)
- Answer
-
\(1 \frac{7}{15}\)
Simplify: \((\frac{2}{9}+\frac{7}{12})+\frac{5}{12}\).
- Answer
-
\(1\frac{2}{9}\)
Use the Properties of Identity, Inverse, and Zero
What happens when we add 0 to any number? Adding 0 doesn’t change the value. For this reason, we call 0 the additive identity. The Identity Property of Addition that states that for any real number \(a,a+0=a\) and \(0+a=a.\)
What happens when we multiply any number by one? Multiplying by 1 doesn’t change the value. So we call 1 the multiplicative identity. The Identity Property of Multiplication that states that for any real number \(a,a·1=a\) and \(1⋅a=a.\)
We summarize the Identity Properties here.
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \\ \\ \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \\ \\ \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\]
What number added to 5 gives the additive identity, 0? We know
.jpg?revision=1&size=bestfit&width=87&height=22)
The missing number was the opposite of the number!
We call \(−a\) the additive inverse of \(a\). The opposite of a number is its additive inverse. A number and its opposite add to zero, which is the additive identity. This leads to the Inverse Property of Addition that states for any real number \(a,a+(−a)=0.\)
What number multiplied by \(\frac{2}{3}\) gives the multiplicative identity, 1? In other words, \(\frac{2}{3}\) times what results in 1? We know
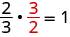
The missing number was the reciprocal of the number!
We call \(\frac{1}{a}\) the multiplicative inverse of a. The reciprocal of a number is its multiplicative inverse. This leads to the Inverse Property of Multiplication that states that for any real number \(a,a\neq 0,a·\frac{1}{a}=1.\)
We’ll formally state the inverse properties here.
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\]
The Identity Property of addition says that when we add 0 to any number, the result is that same number. What happens when we multiply a number by 0? Multiplying by 0 makes the product equal zero.
What about division involving zero? What is \(0÷3\)? Think about a real example: If there are no cookies in the cookie jar and 3 people are to share them, how many cookies does each person get? There are no cookies to share, so each person gets 0 cookies. So, \(0÷3=0.\)
We can check division with the related multiplication fact. So we know \(0÷3=0\) because \(0·3=0\).
Now think about dividing by zero. What is the result of dividing 4 by 0? Think about the related multiplication fact:

Is there a number that multiplied by 0 gives 4? Since any real number multiplied by 0 gives 0, there is no real number that can be multiplied by 0 to obtain 4. We conclude that there is no answer to \(4÷0\) and so we say that division by 0 is undefined.
We summarize the properties of zero here.
Multiplication by Zero: For any real number a,
\[a⋅0=0 \; \; \; 0⋅a=0 \; \; \; \; \text{The product of any number and 0 is 0.}\]
Division by Zero: For any real number a, \(a\neq 0\)
\[\begin{array}{cl} \dfrac{0}{a}=0 & \text{Zero divided by any real number, except itself, is zero.} \\ \dfrac{a}{0} \text{ is undefined} & \text{Division by zero is undefined.} \end{array}\]
We will now practice using the properties of identities, inverses, and zero to simplify expressions.
Simplify: \(−84n+(−73n)+84n.\)
- Answer
-
\(\begin{array}{lc} \text{} & −84n+(−73n)+84n \\ \text{Notice that the first and third terms are} \\ \text{opposites; use the Commutative Property of} & −84n+84n+(−73n) \\ \text{addition to re-order the terms.} \\ \text{Add left to right.} & 0+(−73n) \\ \text{Add.} & −73n \end{array}\)
Simplify: \(−27a+(−48a)+27a\).
- Answer
-
\(−48a\)
Simplify: \(39x+(−92x)+(−39x)\).
- Answer
-
\(−92x\)
Now we will see how recognizing reciprocals is helpful. Before multiplying left to right, look for reciprocals—their product is 1.
Simplify: \(\frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7}\).
- Answer
-
\(\begin{array}{lc} \text{} & \frac{7}{15}⋅\frac{8}{23}⋅\frac{15}{7} \\ \text{Notice the first and third terms} \\ {\text{are reciprocals, so use the Commutative} \\ \text{Property of multiplication to re-order the} \\ \text{factors.}} & \frac{7}{15}·\frac{15}{7}·\frac{8}{23} \\ \text{Multiply left to right.} & 1·\frac{8}{23} \\ \text{Multiply.} & \frac{8}{23} \end{array}\)
Simplify: \(\frac{9}{16}⋅\frac{5}{49}⋅\frac{16}{9}\).
- Answer
-
\(\frac{5}{49}\)
Simplify: \(\frac{6}{17}⋅\frac{11}{25}⋅\frac{17}{6}\).
- Answer
-
\(\frac{11}{25}\)
The next example makes us aware of the distinction between dividing 0 by some number or some number being divided by 0.
Simplify: a. \(\frac{0}{n+5}\), where \(n\neq −5\) b. \(\frac{10−3p}{0}\) where \(10−3p\neq 0.\)
- Answer
-
a.
\(\begin{array}{lc} {} & \dfrac{0}{n+5} \\ \text{Zero divided by any real number except itself is 0.} & 0 \end{array}\)
b.
\(\begin{array}{lc} {} & \dfrac{10−3p}{0} \\ \text{Division by 0 is undefined.} & \text{undefined} \end{array}\)
Simplify: a. \(\frac{0}{m+7}\), where \(m\neq −7\) b. \(\frac{18−6c}{0}\), where \(18−6c\neq 0\).
- Answer
-
a. 0
b. undefined
Simplify: a. \(\frac{0}{d−4}\), where \(d\neq 4\) b. \(\frac{15−4q}{0}\), where \(15−4q\neq 0\).
- Answer
-
a. 0
b. undefined
Simplify Expressions Using the Distributive Property
Suppose that three friends are going to the movies. They each need $9.25—that’s 9 dollars and 1 quarter—to pay for their tickets. How much money do they need all together?
You can think about the dollars separately from the quarters. They need 3 times $9 so $27 and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
\(\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\)
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions.
Simplify: \(3(x+4)\).
- Answer
-
\(\begin{array} {} & 3(x+4) \\ \text{Distribute.} \; \; \; \; \; \; \; \; & 3·x+3·4 \\ \text{Multiply.} & 3x+12 \end{array}\)
Simplify: \(4(x+2)\).
- Answer
-
\(4x8\)
Simplify: \(6(x+7)\).
- Answer
-
\(6x42\)
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in Example would look like this:
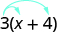
Simplify: \(8(\frac{3}{8}x+\frac{1}{4})\).
- Answer
-
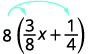
Distribute. 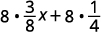
Multiply. 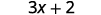
Simplify: \(6(\frac{5}{6}y+\frac{1}{2})\).
- Answer
-
\(5y+3\)
Simplify: \(12(\frac{1}{3}n+\frac{3}{4})\)
- Answer
-
\(4n+9\)
Using the Distributive Property as shown in the next example will be very useful when we solve money applications in later chapters.
Simplify: \(100(0.3+0.25q)\).
- Answer
-
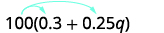
Distribute. 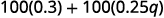
Multiply. 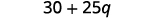
Simplify: \(100(0.7+0.15p).\)
- Answer
-
\(70+15p\)
Simplify: \(100(0.04+0.35d)\).
- Answer
-
\(4+35d\)
When we distribute a negative number, we need to be extra careful to get the signs correct!
Simplify: \(−11(4−3a).\)
- Answer
-
\(\begin{array}{lc} {} & −11(4−3a) \\ \text{Distribute. } \; \; \; \; \; \; \; \; \; \;& −11·4−(−11)·3a \\ \text{Multiply.} & −44−(−33a) \\ \text{Simplify.} & −44+33a \end{array}\)
Notice that you could also write the result as \(33a−44.\) Do you know why?
Simplify: \(−5(2−3a)\).
- Answer
-
\(−10+15a\)
Simplify: \(−7(8−15y).\)
- Answer
-
\(−56+105y\)
In the next example, we will show how to use the Distributive Property to find the opposite of an expression.
Simplify: \(−(y+5)\).
- Answer
-
\(\begin{array}{lc} {} & −(y+5) \\ \text{Multiplying by }−1 \text{ results in the opposite.}& −1(y+5) \\ \text{Distribute.} & −1·y+(−1)·5 \\ \text{Simplify.} & −y+(−5) \\ \text{Simplify.} & −y−5 \end{array} \)
Simplify: \(−(z−11)\).
- Answer
-
\(−z+11\)
Simplify: \(−(x−4)\).
- Answer
-
\(−x+4\)
There will be times when we’ll need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be multiply using the Distributive Property, which removes the parentheses. The next two examples will illustrate this.
Simplify: \(8−2(x+3)\)
- Answer
-
We follow the order of operations. Multiplication comes before subtraction, so we will distribute the 2 first and then subtract.
\(\begin{array}{lc} {} & \text{8−2(x+3)} \\ \text{Distribute.} & 8−2·x−2·3 \\ \text{Multiply.} & 8−2x−6 \\ \text{Combine like terms.} &−2x+2 \end{array}\)
Simplify: \(9−3(x+2)\).
- Answer
-
\(3−3x\)
Simplify: \(7x−5(x+4)\).
- Answer
-
\(2x−20\)
Simplify: \(4(x−8)−(x+3)\).
- Answer
-
\(\begin{array}{lc} {} & 4(x−8)−(x+3) \\ \text{Distribute.} & 4x−32−x−3 \\ \text{Combine like terms.} & 3x−35 \end{array}\)
Simplify: \(6(x−9)−(x+12)\).
- Answer
-
\(5x−66\)
Simplify: \(8(x−1)−(x+5)\).
- Answer
-
\(7x−13\)
All the properties of real numbers we have used in this chapter are summarized here.
| Commutative Property
When adding or multiplying, changing the order gives the same result \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Associative Property
When adding or multiplying, changing the grouping gives the same result. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Distributive Property
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Identity Property \[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Inverse Property
\[\begin{array}{lc} \textbf{of addition } \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Properties of Zero \[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Key Concepts
| Commutative Property When adding or multiplying, changing the order gives the same result \[\begin{array}{lll} \textbf{of Addition} & \text{If }a \text{ and }b \text{are real numbers, then} & a+b=b+a. \\ \textbf{of Multiplication} & \text{If }a \text{ and }b \text{are real numbers, then} & a·b=b·a. \end{array} \] |
| Associative Property When adding or multiplying, changing the grouping gives the same result. \[\begin{array}{lll} \textbf{of Addition} & \text{If }a,b, \text{ and }c \text{ are real numbers, then} & (a+b)+c=a+(b+c). \\ \textbf{of Multiplication} & \text{If }a,b,\text{ and }c \text{ are real numbers, then} & (a·b)·c=a·(b·c). \end{array} \] |
| Distributive Property
\[\begin{array}{lc} \text{If }a,b \text{,and }c \text{are real numbers, then} \; \; \; \; \; & a(b+c)=ab+ac \\ {} & (b+c)a=ba+ca \\ {} & a(b−c)=ab−ac \\{} & (b−c)a=ba−ca \end{array}\] |
| Identity Property
\[\begin{array}{ll} \textbf{of Addition} \text{ For any real number }a:a+0=a & 0+a=a \\ \;\;\;\; \textbf{0} \text{ is the } \textbf{additive identity} \\ \textbf{of Multiplication} \text{ For any real number } a:a·1=a & 1·a=a \\ \;\;\;\; \textbf{1} \text{ is the } \textbf{multiplicative identity} \end{array}\] |
| Inverse Property
\[\begin{array}{lc} \textbf{of addition} \text{For any real number }a, & a+(−a)=0 \\ \;\;\;\; −a \text{ is the } \textbf{additive inverse }\text{ of }a & {} \\ \;\;\;\; \text{A number and its } \textit{opposite } \text{add to zero.} \\ \\ \\ \textbf{of multiplication } \text{For any real number }a,a\neq 0 & a·\dfrac{1}{a}=1 \\ \;\;\;\;\;\dfrac{1}{a} \text{ is the } \textbf{multiplicative inverse} \text{ of }a \\ \;\;\;\; \text{A number and its } \textit{reciprocal} \text{ multiply to one.} \end{array}\] |
| Properties of Zero
\[\begin{array}{lc} \text{For any real number }a, & a·0=0 \\ {} & 0·a=0 \\ \text{For any real number }a,a\neq 0, & \dfrac{0}{a}=0 \\ \text{For any real number }a, & \dfrac{a}{0} \text{ is undefined} \end{array}\] |
Glossary
- additive identity
- The number 0 is the additive identity because adding 0 to any number does not change its value.
- additive inverse
- The opposite of a number is its additive inverse.
- multiplicative identity
- The number 1 is the multiplicative identity because multiplying 1 by any number does not change its value.
- multiplicative inverse
- The reciprocal of a number is its multiplicative inverse.


