12.3: Defining Equivalence or Similarity
( \newcommand{\kernel}{\mathrm{null}\,}\)
What do we mean when we say that two actors have "similar" patterns of relations, and hence are both members of the same role or social position? Network analysts most broadly defines two nodes (or other more elaborate structures) as similar if they fall in the same "equivalence class". Frankly, that's no immediate help. But it does say that there is something that would cause us to say two actors (or other structures) are members of a "class" that is different from other "classes".
Now it becomes a question of what features of an actor's position place them into a "class" with other actors? In what way are they "equivalent"?
There are many ways in which actors could be defined as "equivalent" based on their relations with others. For example, we could create two "equivalence classes" of actors with out-degree of zero, and actors with out-degree of more than zero. Indeed, a very large number of the algorithms we've examined group sets of actors into categories based on some commonality in their positions in graphs.
Three particular definitions of "equivalence" have been particularly useful in applying graph theory to the understanding of "social roles" and "structural positions". We will look at these in the next three sections on "structural equivalence", "automorphic equivalence", and "regular equivalence". Of these, "automorphic" has rarely been used in substantive work.
The basic ideas of these three kinds of equivalence are easily illustrated with a simple graph (developed by Wasserman and Faust). Consider Figure 12.1, a simple graph of the relations among nine actors "A" to "I".
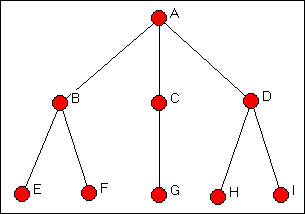
Figure 12.1: Wasserman-Faust network to illustrate equivalence classes
This graph provides particularly clear examples of how structural, automorphic, and regular equivalence differ. Let's look in more detail at these ideas, starting with the most restrictive notion of what it means for actors to be equivalent.
Structural Equivalence
Two nodes are said to be exactly structurally equivalent if they have the same relationships to all other nodes. Structural equivalence is easy to grasp (though it can be operationalized in a number of ways) because it is very specific: two actors must be exactly substitutable in order to be structurally equivalent.
In Figure
- There is no actor who has exactly the same set of ties as actor A (ties to B, C, and D), so actor A is in a class by itself.
- The same is true for actors B, C, and D. Each of these actors has a unique set of ties to others, so they form three classes, each with one member.
- E and F, however, fall in the same structural equivalence class. Each has a single tie; and that tie is to actor B. Since E and F have exactly the same pattern of ties with all other actors, they are structurally equivalent.
- Actor G, again, is in a class by itself. Its profile of ties with the other nodes in the diagram is unique.
- Finally, actors H and I fall in the same structural equivalence class. That is, they have exactly the same pattern of ties to all other actors.
Actors that are structurally equivalent are in identical "positions" in the structure of the diagram. Whatever opportunities and constraints operate on one member of a class are also present for the others. The nodes in a structural equivalence class are, in a sense, in the same position with regard to all other actors.
Because exact structural equivalence is likely to be rare (particularly in large networks), we often are interested in examining the degree of structural equivalence, rather than the simple presence or absence of exact equivalence.
Structural equivalence is the "strongest" form of equivalence that network analysts usually consider. If we soften the requirements just a bit, we can often find some interesting other patterns of equivalence.
Automorphic Equivalence
The idea of structural equivalence is powerful because it identifies actors that have the same position, or who are completely substitutable. But, even intuitively, you can probably imagine other "less strict" definitions of what it means for two actors to be similar or equivalent.
Suppose that the graph in Figure
Even though actor B and actor D are not structurally equivalent (they doe have the same boss, but not the same workers), they do seem to be "equivalent" in a different sense. Both manager B and manager D report to a boss (in this case, the same boss), and each has exactly two workers. These are different people, but the two managers seem somehow equivalent. If we swapped them, and also swapped the four workers, all of the distances among all the actors in the graph would be exactly identical. In fact, actors B and D form an "automorphic" equivalence class.
In Figure
The idea of automorphic equivalence is that sets of actors can be equivalent by being embedded in local structures that have the same patterns of ties - "parallel" structures. Large scale populations of social actors (perhaps like hamburger restaurant chains) can display a great deal of this sort of "structural replication". The faces are different, but the structures are identical.
Note that the less strict definition of "equivalence" had reduced the number of classes. If we are willing to go one important step further, we can reduce the complexity still further.
Regular Equivalence
Two nodes are said to be regularly equivalent if they have the same profile of ties with other sets of actors that are also regularly equivalent. This is a complicated way of saying something that we recognize intuitively.
Two mothers, for example, are "equivalent" because each has a certain pattern of ties with a husband, children, and in-laws (for one example - but one that is very culturally relative). The two mothers do not have ties to the same husband (usually) or the same children or in-laws. That is, they are not "structurally equivalent". Because different mothers may have different numbers of husbands, children, and in-laws, they will not be automorphically equivalent. But they are similar because they have the same relationships with some member or members of another set of actors (who are themselves regarded as equivalent because of the similarity of their ties to a member of the set "mother").
This is an obvious notion, but a critical one. Regular equivalence sets describe the "social roles" that are the basic building blocks of all social institutions. Actors that are regularly equivalent to not necessarily fall in the same network positions or locations with respect to other individual actors; rather, they have the same kinds of relationships with some members of other sets of actors.
In Figure
The easiest class to see is the give actors across the bottom of the figure (E, F, G, H, and I). These actors are regularly equivalent to one another because a) they have no tie with any actor in the first class (that is, with actor A) and b) each has a tie with an actor in the second class (either B, C, or D). Each of the five actors, then, has an identical pattern of ties with actors in the other classes.
Actors B, C, and D form a class because a) they have a tie with a member of the first class (that is, with actor A) and b) they each have a tie with a member of the third class. B and D actually have ties with two members of the third class, whereas actor C has a tie to only one member of the third class; this doesn't matter, as there is a tie to some member of the third class.
Actor A is in a class by itself, defined by a) a tie to at least one member of class two and b) no tie to any member of class three.
As with structural and automorphic equivalence, exact regular equivalence may be rare in a large population with many equivalence classes. Approximate regular equivalence can be very meaningful though, because it gets at the notion of which actors fall in which social roles, and how social roles (not role occupants) relate to one another.


