5.10: Ratios and Rate (Part 1)
- Page ID
- 5003
- Write a ratio as a fraction
- Write a rate as a fraction
- Find unit rates
- Find unit price
- Translate phrases to expressions with fractions
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{16}{24}\). If you missed this problem, review Example 4.3.1.
- Divide: 2.76 ÷ 11.5. If you missed this problem, review Example 5.4.9.
- Simplify: \(\dfrac{1 \dfrac{1}{2}}{2 \dfrac{3}{4}}\). If you missed this problem, review Example 4.5.7.
Write a Ratio as a Fraction
When you apply for a mortgage, the loan officer will compare your total debt to your total income to decide if you qualify for the loan. This comparison is called the debt-to-income ratio. A ratio compares two quantities that are measured with the same unit. If we compare a and b , the ratio is written as a to b, \(\dfrac{a}{b}\), or a:b.
A ratio compares two numbers or two quantities that are measured with the same unit. The ratio of a to b is written a to b, \(\dfrac{a}{b}\), or a:b.
In this section, we will use the fraction notation. When a ratio is written in fraction form, the fraction should be simplified. If it is an improper fraction, we do not change it to a mixed number. Because a ratio compares two quantities, we would leave a ratio as \(\dfrac{4}{1}\) instead of simplifying it to 4 so that we can see the two parts of the ratio.
Write each ratio as a fraction: (a) 15 to 27 (b) 45 to 18.
Solution
(a) 15 to 27
| Write as a fraction with the first number in the numerator and the second in the denominator. | $$\dfrac{15}{27}$$ |
| Simplify the fraction. | $$\dfrac{5}{9}$$ |
(b) 45 to 18
| Write as a fraction with the first number in the numerator and the second in the denominator. | $$\dfrac{45}{18}$$ |
| Simplify. | $$\dfrac{5}{2}$$ |
We leave the ratio in (b) as an improper fraction.
Write each ratio as a fraction: (a) 21 to 56 (b) 48 to 32.
- Answer a
-
\(\dfrac{3}{8}\)
- Answer b
-
\(\dfrac{3}{2}\)
Write each ratio as a fraction: (a) 27 to 72 (b) 51 to 34.
- Answer a
-
\(\dfrac{1}{1}\)
- Answer b
-
\(\dfrac{3}{2}\)
Ratios Involving Decimals
We will often work with ratios of decimals, especially when we have ratios involving money. In these cases, we can eliminate the decimals by using the Equivalent Fractions Property to convert the ratio to a fraction with whole numbers in the numerator and denominator.
For example, consider the ratio 0.8 to 0.05. We can write it as a fraction with decimals and then multiply the numerator and denominator by 100 to eliminate the decimals.
\[\dfrac{0.8}{0.05}\]
\[\dfrac{(0.8) \textcolor{red}{100}}{(0.05) \textcolor{red}{100}}\]
\[\dfrac{80}{5}\]
Do you see a shortcut to find the equivalent fraction? Notice that 0.8 = \(\dfrac{8}{10}\) and 0.05 = \(\dfrac{5}{100}\). The least common denominator of \(\dfrac{8}{10}\) and 5 100 is 100. By multiplying the numerator and denominator of \(\dfrac{0.8}{0.05}\) by 100, we ‘moved’ the decimal two places to the right to get the equivalent fraction with no decimals. Now that we understand the math behind the process, we can find the fraction with no decimals like this:
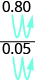
| "Move" the decimal 2 places. | $$\dfrac{80}{5}$$ |
| Simplify. | $$\dfrac{16}{1}$$ |
You do not have to write out every step when you multiply the numerator and denominator by powers of ten. As long as you move both decimal places the same number of places, the ratio will remain the same.
Write each ratio as a fraction of whole numbers: (a) 4.8 to 11.2 (b) 2.7 to 0.54
Solution
(a) 4.8 to 11.2
| Write as a fraction. | $$\dfrac{4.8}{11.2}$$ |
| Rewrite as an equivalent fraction without decimals, by moving both decimal points 1 place to the right. | $$\dfrac{48}{112}$$ |
| Simplify. | $$\dfrac{3}{7}$$ |
So 4.8 to 11.2 is equivalent to \(\dfrac{3}{7}\).
(b) 2.7 to 0.54
| Write as a fraction. | $$\dfrac{2.7}{0.54}$$ |
| The numerator has one decimal place and the denominator has 2. To clear both decimals we need to move the decimal 2 places to the right. | $$\dfrac{270}{54}$$ |
| Simplify. | $$\dfrac{5}{1}$$ |
So 2.7 to 0.54 is equivalent to \(\dfrac{5}{1}\).
Write each ratio as a fraction: (a) 4.6 to 11.5 (b) 2.3 to 0.69.
- Answer a
-
\(\dfrac{2}{5}\)
- Answer b
-
\(\dfrac{10}{3}\)
Write each ratio as a fraction: (a) 3.4 to 15.3 (b) 3.4 to 0.68.
- Answer a
-
\(\dfrac{2}{9}\)
- Answer b
-
\(\dfrac{5}{1}\)
Some ratios compare two mixed numbers. Remember that to divide mixed numbers, you first rewrite them as improper fractions.
Write the ratio of \(1 \dfrac{1}{4}\) to \(2 \dfrac{3}{8}\) as a fraction.
Solution
| Write as a fraction. | $$\dfrac{1 \dfrac{1}{4}}{2 \dfrac{3}{8}}$$ |
| Convert the numerator and denominator to improper fractions. | $$\dfrac{\dfrac{5}{4}}{\dfrac{19}{8}}$$ |
| Rewrite as a division of fractions. | $$\dfrac{5}{4} \div \dfrac{19}{8}$$ |
| Invert the divisor and multiply. | $$\dfrac{5}{4} \cdot \dfrac{8}{19}$$ |
| Simplify. | $$\dfrac{10}{19}$$ |
Write each ratio as a fraction: \(1 \dfrac{3}{4}\) to \(2 \dfrac{5}{8}\).
- Answer
-
\(\dfrac{2}{3}\
Write each ratio as a fraction: \(1 \dfrac{1}{8}\) to \(2 \dfrac{3}{4}\).
- Answer
-
\(\dfrac{9}{22}\)
Applications of Ratios
One real-world application of ratios that affects many people involves measuring cholesterol in blood. The ratio of total cholesterol to HDL cholesterol is one way doctors assess a person's overall health. A ratio of less than 5 to 1 is considered good.
Hector's total cholesterol is 249 mg/dl and his HDL cholesterol is 39 mg/dl. (a) Find the ratio of his total cholesterol to his HDL cholesterol. (b) Assuming that a ratio less than 5 to 1 is considered good, what would you suggest to Hector?
Solution
(a) First, write the words that express the ratio. We want to know the ratio of Hector's total cholesterol to his HDL cholesterol.
| Write as a fraction. | $$\dfrac{total\; cholesterol}{HDL\; cholesterol}$$ |
| Substitute the values. | $$\dfrac{249}{39}$$ |
| Simplify. | $$\dfrac{83}{13}$$ |
(b) Is Hector's cholesterol ratio ok? If we divide 83 by 13 we obtain approximately 6.4, so \(\dfrac{83}{13} \approx \dfrac{6.4}{1}\). Hector's cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
Find the patient's ratio of total cholesterol to HDL cholesterol using the given information. Total cholesterol is 185 mg/dL and HDL cholesterol is 40 mg/dL.
- Answer
-
\(\dfrac{37}{8}\
Find the patient’s ratio of total cholesterol to HDL cholesterol using the given information. Total cholesterol is 204 mg/dL and HDL cholesterol is 38 mg/dL.
- Answer
-
\(\dfrac{102}{19}\
Ratios of Two Measurements in Different Units
To find the ratio of two measurements, we must make sure the quantities have been measured with the same unit. If the measurements are not in the same units, we must first convert them to the same units.
We know that to simplify a fraction, we divide out common factors. Similarly in a ratio of measurements, we divide out the common unit.
The Americans with Disabilities Act (ADA) Guidelines for wheel chair ramps require a maximum vertical rise of 1 inch for every 1 foot of horizontal run. What is the ratio of the rise to the run?
Solution
In a ratio, the measurements must be in the same units. We can change feet to inches, or inches to feet. It is usually easier to convert to the smaller unit, since this avoids introducing more fractions into the problem. Write the words that express the ratio.
| Write the ratio as a fraction. | $$\dfrac{rise}{run}$$ |
| Substitute in the given values. | $$\dfrac{1\; inch}{1\; foot}$$ |
| Convert 1 foot to inches. | $$\dfrac{1\; inch}{12\; inches}$$ |
| Simplify, dividing out common factors and units. | $$\dfrac{1}{12}$$ |
So the ratio of rise to run is 1 to 12. This means that the ramp should rise 1 inch for every 12 inches of horizontal run to comply with the guidelines.
Find the ratio of the first length to the second length: 32 inches to 1 foot.
- Answer
-
\(\dfrac{8}{3}\
Find the ratio of the first length to the second length: 1 foot to 54 inches.
- Answer a
-
\(\dfrac{2}{9}\
Write a Rate as a Fraction
Frequently we want to compare two different types of measurements, such as miles to gallons. To make this comparison, we use a rate. Examples of rates are 120 miles in 2 hours, 160 words in 4 minutes, and $5 dollars per 64 ounces.
A rate compares two quantities of different units. A rate is usually written as a fraction.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.
Bob drove his car 525 miles in 9 hours. Write this rate as a fraction.
Solution
| Write as a fraction, with 525 miles in the numerator and 9 hours in the denominator. | $$\dfrac{525\; miles}{9\; hours}$$ |
| $$\dfrac{175\; miles}{3\; hours}$$ |
So 525 miles in 9 hours is equivalent to \(\dfrac{175\; miles}{3\; hours}\).
Write the rate as a fraction: 492 miles in 8 hours.
- Answer
-
\(\dfrac{123\; miles}{2\; hours}\)
Write the rate as a fraction: 242 miles in 6 hours.
- Answer
-
\(\dfrac{121\; miles}{3\; hours}\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


