5.4: Decimal Operations (Part 2)
- Page ID
- 6445
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Divide Decimals
Just as with multiplication, division of decimals is very much like dividing whole numbers. We just have to figure out where the decimal point must be placed.
To understand decimal division, let’s consider the multiplication problem
\[(0.2)(4) = 0.8\]
Remember, a multiplication problem can be rephrased as a division problem. So we can write 0.8 ÷ 4 = 0.2 We can think of this as “If we divide 8 tenths into four groups, how many are in each group?” Figure \(\PageIndex{1}\) shows that there are four groups of two-tenths in eight-tenths. So 0.8 ÷ 4 = 0.2.

Figure \(\PageIndex{1}\)
Using long division notation, we would write
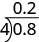
Notice that the decimal point in the quotient is directly above the decimal point in the dividend.
To divide a decimal by a whole number, we place the decimal point in the quotient above the decimal point in the dividend and then divide as usual. Sometimes we need to use extra zeros at the end of the dividend to keep dividing until there is no remainder.
Step 1. Write as long division, placing the decimal point in the quotient above the decimal point in the dividend.
Step 2. Divide as usual.
Divide: 0.12 ÷ 3.
Solution
| Write as long division, placing the decimal point in the quotient above the decimal point in the dividend. | 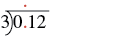 |
| Divide as usual. Since 3 does not go into 0 or 1 we use zeros as placeholders. | 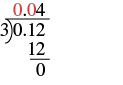 |
0.12 ÷ 3 = 0.04
Divide: 0.28 ÷ 4.
- Answer
-
\(0.07\)
Divide: 0.56 ÷ 7.
- Answer
-
\(0.08\)
In everyday life, we divide whole numbers into decimals—money—to find the price of one item. For example, suppose a case of 24 water bottles cost $3.99. To find the price per water bottle, we would divide $3.99 by 24, and round the answer to the nearest cent (hundredth).
Divide: $3.99 ÷ 24.
Solution
| Place the decimal point in the quotient above the decimal point in the dividend. | 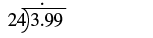 |
| Divide as usual. When do we stop? Since this division involves money, we round it to the nearest cent (hundredth). To do this, we must carry the division to the thousandths place. |  |
| Round to the nearest cent. | $$ $0.166 \approx $0.17$$ |
$3.99 ÷ 24 ≈ $0.17
This means the price per bottle is 17 cents.
Divide: $6.99 ÷ 36.
- Answer
-
\($0.19\)
Divide: $4.99 ÷ 12.
- Answer
-
\($0.42\)
Divide a Decimal by Another Decimal
So far, we have divided a decimal by a whole number. What happens when we divide a decimal by another decimal? Let’s look at the same multiplication problem we looked at earlier, but in a different way.
\[(0.2)(4) = 0.8\]
Remember, again, that a multiplication problem can be rephrased as a division problem. This time we ask, “Ho w many times does 0.2 go into 0.8?” Because (0.2)(4) = 0.8, we can say that 0.2 goes into 0.8 four times. This means that 0.8 divided by 0.2 is 4.
\[0.8 \div 0.2 = 4\]

We would get the same answer, 4, if we divide 8 by 2, both whole numbers. Why is this so? Let’s think about the division problem as a fraction.
\[\dfrac{0.8}{0.2}\]
\[\dfrac{(0.8)10}{(0.2)10}\]
\[\dfrac{8}{2}\]
\[4\]
We multiplied the numerator and denominator by 10 and ended up just dividing 8 by 2. To divide decimals, we multiply both the numerator and denominator by the same power of 10 to make the denominator a whole number. Because of the Equivalent Fractions Property, we haven’t changed the value of the fraction. The effect is to move the decimal points in the numerator and denominator the same number of places to the right.
We use the rules for dividing positive and negative numbers with decimals, too. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient with the appropriate sign. It may help to review the vocabulary for division:
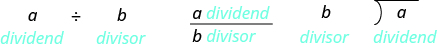
Step 1. Determine the sign of the quotient.
Step 2. Make the divisor a whole number by moving the decimal point all the way to the right. Move the decimal point in the dividend the same number of places to the right, writing zeros as needed.
Step 3. Divide. Place the decimal point in the quotient above the decimal point in the dividend.
Step 4. Write the quotient with the appropriate sign.
Divide: −2.89 ÷ (3.4).
Solution
| Determine the sign of the quotient. | The quotient will be negative. |
| Make the divisor the whole number by 'moving' the decimal point all the way to the right. 'Move' the decimal point in the dividend the same number of places to the right. |  |
| Divide. Place the decimal point in the quotient above the decimal point in the dividend. Add zeros as needed until the remainder is zero. | 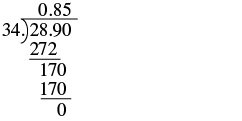 |
| Write the quotient with the appropriate sign. | −2.89 ÷ (3.4) = −0.85 |
Divide: −1.989 ÷ 5.1.
- Answer
-
\(-0.39\)
Divide: −2.04 ÷ 5.1.
- Answer
-
\(-0.4\)
Divide: −25.65 ÷ (−0.06).
Solution
| The signs are the same. | The quotient is positive. |
| Make the divisor a whole number by 'moving' the decimal point all the way to the right. 'Move' the decimal point in the dividend the same number of places. |  |
| Divide. Place the decimal point in the quotient above the decimal point in the dividend. | 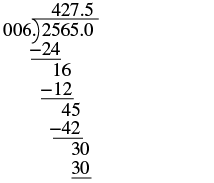 |
| Write the quotient with the appropriate sign. | −25.65 ÷ (−0.06) = 427.5 |
Divide: −23.492 ÷ (−0.04).
- Answer
-
\(587.3\)
Divide: −4.11 ÷ (−0.12).
- Answer
-
\(34.25\)
Now we will divide a whole number by a decimal number.
Divide: 4 ÷ (0.05).
Solution
| The signs are the same. | The quotient is positive. |
| Make the divisor a whole number by 'moving' the decimal point all the way to the right. Move the decimal point in the dividend the same number of places, adding zeros as needed. |  |
| Divide. Place the decimal point in the quotient above the decimal point in the dividend. | 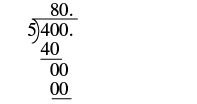 |
| Write the quotient with the appropriate sign. | 4 ÷ 0.05 = 80 |
We can relate this example to money. How many nickels are there in four dollars? Because 4 ÷ 0.05 = 80, there are 80 nickels in $4.
Divide: 6 ÷ 0.03.
- Answer
-
\(200\)
Divide: 7 ÷ 0.02
- Answer
-
\(350\)
Use Decimals in Money Applications
We often apply decimals in real life, and most of the applications involving money. The Strategy for Applications we used in The Language of Algebra gives us a plan to follow to help find the answer. Take a moment to review that strategy now.
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
Paul received $50 for his birthday. He spent $31.64 on a video game. How much of Paul’s birthday money was left?
Solution
| What are you asked to find? | How much did Paul have left? |
| Write a phrase. | $50 less $31.64 |
| Translate. | 50 − 31.64 |
| Simplify. | 18.36 |
| Write a sentence. | Paul has $18.36 left. |
Nicole earned $35 for babysitting her cousins, then went to the bookstore and spent $18.48 on books and coffee. How much of her babysitting money was left?
- Answer
-
\($16.52\)
Amber bought a pair of shoes for $24.75 and a purse for $36.90. The sales tax was $4.32. How much did Amber spend?
- Answer
-
\($65.97\)
Jessie put 8 gallons of gas in her car. One gallon of gas costs $3.529. How much does Jessie owe for the gas? (Round the answer to the nearest cent.)
Solution
| What are you asked to find? | How much did Jessie owe for all the gas? |
| Write a phrase. | 8 times the cost of one gallon of gas |
| Translate. | 8($3.529) |
| Simplify. | $28.232 |
| Round to the nearest cent. | $28.23 |
| Write a sentence. | Jessie owes $28.23 for her gas purchase. |
Hector put 13 gallons of gas into his car. One gallon of gas costs $3.175. How much did Hector owe for the gas? Round to the nearest cent.
- Answer
-
\($41.28\)
Christopher bought 5 pizzas for the team. Each pizza cost $9.75. How much did all the pizzas cost?
- Answer
-
\($48.75\)
Four friends went out for dinner. They shared a large pizza and a pitcher of soda. The total cost of their dinner was $31.76. If they divide the cost equally, how much should each friend pay?
Solution
| What are you asked to find? | How much should each friend pay? |
| Write a phrase. | $31.76 divided equally among the four friends. |
| Translate to an expression. | $31.76 ÷ 4 |
| Simplify. | $7.94 |
| Write a sentence. | Each friend should pay $7.94 for his share of the dinner. |
Six friends went out for dinner. The total cost of their dinner was $92.82. If they divide the bill equally, how much should each friend pay?
- Answer
-
\($15.47\)
Chad worked 40 hours last week and his paycheck was $570. How much does he earn per hour?
- Answer
-
\($14.25\)
Be careful to follow the order of operations in the next example. Remember to multiply before you add.
Marla buys 6 bananas that cost $0.22 each and 4 oranges that cost $0.49 each. How much is the total cost of the fruit?
Solution
| What are you asked to find? | How much is the total cost of the fruit? |
| Write a phrase. | 6 times the cost of each banana plus 4 times the cost of each orange |
| Translate to an expression. | 6($0.22) + 4($0.49) |
| Simplify. | $1.32 + $1.96 |
| Add. | $3.28 |
| Write a sentence. | Marla's total cost for the fruit is $3.28. |
Suzanne buys 3 cans of beans that cost $0.75 each and 6 cans of corn that cost $0.62 each. How much is the total cost of these groceries?
- Answer
-
\($5.97\)
Lydia bought movie tickets for the family. She bought two adult tickets for $9.50 each and four children’s tickets for $6.00 each. How much did the tickets cost Lydia in all?
- Answer
-
\($43.00\)
Adding and Subtracting Decimals
Multiplying Decimals
Multiplying by Powers of Ten
Dividing Decimals
Dividing by Powers of Ten
Practice Makes Perfect
Add and Subtract Decimals
In the following exercises, add or subtract.
- 16.92 + 7.56
- 18.37 + 9.36
- 256.37 − 85.49
- 248.25 − 91.29
- 21.76 − 30.99
- 15.35 − 20.88
- 37.5 + 12.23
- 38.6 + 13.67
- −16.53 − 24.38
- −19.47 − 32.58
- −38.69 + 31.47
- −29.83 + 19.76
- −4.2 + (− 9.3)
- −8.6 + (− 8.6)
- 100 − 64.2
- 100 − 65.83
- 72.5 − 100
- 86.2 − 100
- 15 + 0.73
- 27 + 0.87
- 2.51 + 40
- 9.38 + 60
- 91.75 − (− 10.462)
- 94.69 − (− 12.678)
- 55.01 − 3.7
- 59.08 − 4.6
- 2.51 − 7.4
- 3.84 − 6.1
Multiply Decimals
In the following exercises, multiply.
- (0.3)(0.4)
- (0.6)(0.7)
- (0.24)(0.6)
- (0.81)(0.3)
- (5.9)(7.12)
- (2.3)(9.41)
- (8.52)(3.14)
- (5.32)(4.86)
- (−4.3)(2.71)
- (− 8.5)(1.69)
- (−5.18)(− 65.23)
- (− 9.16)(− 68.34)
- (0.09)(24.78)
- (0.04)(36.89)
- (0.06)(21.75)
- (0.08)(52.45)
- (9.24)(10)
- (6.531)(10)
- (55.2)(1,000)
- (99.4)(1,000)
Divide Decimals
In the following exercises, divide.
- 0.15 ÷ 5
- 0.27 ÷ 3
- 4.75 ÷ 25
- 12.04 ÷ 43
- $8.49 ÷ 12
- $16.99 ÷ 9
- $117.25 ÷ 48
- $109.24 ÷ 36
- 0.6 ÷ 0.2
- 0.8 ÷ 0.4
- 1.44 ÷ (− 0.3)
- 1.25 ÷ (− 0.5)
- −1.75 ÷ (− 0.05)
- −1.15 ÷ (− 0.05)
- 5.2 ÷ 2.5
- 6.5 ÷ 3.25
- 12 ÷ 0.08
- 5 ÷ 0.04
- 11 ÷ 0.55
- 14 ÷ 0.35
Mixed Practice
In the following exercises, simplify.
- 6(12.4 − 9.2)
- 3(15.7 − 8.6)
- 24(0.5) + (0.3)2
- 35(0.2) + (0.9)2
- 1.15(26.83 + 1.61)
- 1.18(46.22 + 3.71)
- $45 + 0.08($45)
- $63 + 0.18($63)
- 18 ÷ (0.75 + 0.15)
- 27 ÷ (0.55 + 0.35)
- (1.43 + 0.27) ÷ (0.9 − 0.05)
- (1.5 − 0.06) ÷ (0.12 + 0.24)
- [$75.42 + 0.18($75.42)] ÷ 5
- [$56.31 + 0.22($56.31)] ÷ 4
Use Decimals in Money Applications
In the following exercises, use the strategy for applications to solve.
- Spending money Brenda got $40 from the ATM. She spent $15.11 on a pair of earrings. How much money did she have left?
- Spending money Marissa found $20 in her pocket. She spent $4.82 on a smoothie. How much of the $20 did she have left?
- Shopping Adam bought a t-shirt for $18.49 and a book for $8.92 The sales tax was $1.65. How much did Adam spend?
- Restaurant Roberto’s restaurant bill was $20.45 for the entrée and $3.15 for the drink. He left a $4.40 tip. How much did Roberto spend?
- Coupon Emily bought a box of cereal that cost $4.29. She had a coupon for $0.55 off, and the store doubled the coupon. How much did she pay for the box of cereal?
- Coupon Diana bought a can of coffee that cost $7.99. She had a coupon for $0.75 off, and the store doubled the coupon. How much did she pay for the can of coffee?
- Diet Leo took part in a diet program. He weighed 190 pounds at the start of the program. During the first week, he lost 4.3 pounds. During the second week, he had lost 2.8 pounds. The third week, he gained 0.7 pounds. The fourth week, he lost 1.9 pounds. What did Leo weigh at the end of the fourth week?
- Snowpack On April 1, the snowpack at the ski resort was 4 meters deep, but the next few days were very warm. By April 5, the snow depth was 1.6 meters less. On April 8, it snowed and added 2.1 meters of snow. What was the total depth of the snow?
- Coffee Noriko bought 4 coffees for herself and her coworkers. Each coffee was $3.75. How much did she pay for all the coffees?
- Subway Fare Arianna spends $4.50 per day on subway fare. Last week she rode the subway 6 days. How much did she spend for the subway fares? 187. Income Mayra earns $9.25 per hour. Last week she worked 32 hours. How much did she earn?
- Income Peter earns $8.75 per hour. Last week he worked 19 hours. How much did he earn?
- Hourly Wage Alan got his first paycheck from his new job. He worked 30 hours and earned $382.50. How much does he earn per hour?
- Hourly Wage Maria got her first paycheck from her new job. She worked 25 hours and earned $362.50. How much does she earn per hour?
- Restaurant Jeannette and her friends love to order mud pie at their favorite restaurant. They always share just one piece of pie among themselves. With tax and tip, the total cost is $6.00. How much does each girl pay if the total number sharing the mud pie is (a) 2? (b) 3? (c) 4? (d) 5? (e) 6?
- Pizza Alex and his friends go out for pizza and video games once a week. They share the cost of a $15.60 pizza equally. How much does each person pay if the total number sharing the pizza is (a) 2? (b) 3? (c) 4? (d) 5? (e) 6?
- Fast Food At their favorite fast food restaurant, the Carlson family orders 4 burgers that cost $3.29 each and 2 orders of fries at $2.74 each. What is the total cost of the order?
- Home Goods Chelsea needs towels to take with her to college. She buys 2 bath towels that cost $9.99 each and 6 washcloths that cost $2.99 each. What is the total cost for the bath towels and washcloths?
- Zoo The Lewis and Chousmith families are planning to go to the zoo together. Adult tickets cost $29.95 and children’s tickets cost $19.95. What will the total cost be for 4 adults and 7 children?
- Ice Skating Jasmine wants to have her birthday party at the local ice skating rink. It will cost $8.25 per child and $12.95 per adult. What will the total cost be for 12 children and 3 adults?
Everyday Math
- Paycheck Annie has two jobs. She gets paid $14.04 per hour for tutoring at City College and $8.75 per hour at a coffee shop. Last week she tutored for 8 hours and worked at the coffee shop for 15 hours. (a) How much did she earn? (b) If she had worked all 23 hours as a tutor instead of working both jobs, how much more would she have earned?
- Paycheck Jake has two jobs. He gets paid $7.95 per hour at the college cafeteria and $20.25 at the art gallery. Last week he worked 12 hours at the cafeteria and 5 hours at the art gallery. (a) How much did he earn? (b) If he had worked all 17 hours at the art gallery instead of working both jobs, how much more would he have earned?
Writing Exercises
- In the 2010 winter Olympics, two skiers took the silver and bronze medals in the Men's Super-G ski event. The silver medalist's time was 1 minute 30.62 seconds and bronze medalist's time was 1 minute 30.65 seconds. Whose time was faster? Find the difference in their times and then write the name of that decimal.
- Find the quotient of 0.12 ÷ 0.04 and explain in words all the steps taken.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
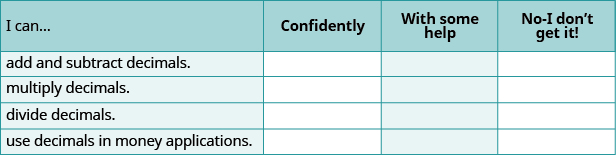
(b) After reviewing this checklist, what will you do to become confident for all objectives?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


