6.2: Related Rates
- Page ID
- 450
Suppose we have two variables \(x\) and \(y\) (in most problems the letters will be different, but for now let's use \(x\) and \(y\)) which are both changing with time. A "related rates'' problem is a problem in which we know one of the rates of change at a given instant---say, \( \dot x = dx/dt\)---and we want to find the other rate \(\dot y = dy/dt\) at that instant. (The use of \(\dot x\) to mean \(dx/dt\) goes back to Newton and is still used for this purpose, especially by physicists.)
If \(y\) is written in terms of \(x\), i.e., \(y=f(x)\), then this is easy to do using the chain rule: $$ \dot y = {dy\over dt}={dy\over dx}\cdot{dx\over dt}={dy\over dx}\dot x. $$ That is, find the derivative of \(f(x)\), plug in the value of \(x\) at the instant in question, and multiply by the given value of \( \dot{x}=dx/dt\) to get \( \dot{y}=dy/dt\).
Using the chain rule, \( dy/dt = 2x\cdot dx/dt\). At \(t=5\) we know that \(x=6\) and \(dx/dt=3\), so \(dy/dt = 2\cdot 6\cdot 3 = 36\).
To summarize, here are the steps in doing a related rates problem:
- Decide what the two variables are.
- Find an equation relating them.
- Take \(d/dt\) of both sides.
- Plug in all known values at the instant in question.
- Solve for the unknown rate.
.
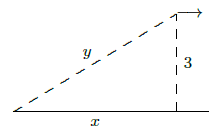
Figure 6.2.1. Receding airplane.
Because the plane is in level flight directly away from you, the rate at which \(x\) changes is the speed of the plane, \(dx/dt=500\). The distance between you and the plane is \(y\); it is \(dy/dt\) that we wish to know. By the Pythagorean Theorem we know that \( x^2+9=y^2\). Taking the derivative: $$ 2x \dot x = 2y\dot y.$$ We are interested in the time at which \(x=4\); at this time we know that \(4^2+9=y^2\), so \(y=5\). Putting together all the information we get $$2(4)(500)=2(5)\dot y.$$ Thus, \( \dot y=400\) mph.
Here the variables are the radius \(r\) and the volume \(V\). We know \(dV/dt\), and we want \(dr/dt\). The two variables are related by means of the equation \( V=4\pi r^3/3\). Taking the derivative of both sides gives \( dV/dt=4\pi r^2\dot r\). We now substitute the values we know at the instant in question: \( 7=4\pi
The water forms a conical shape within the big cone; its height and base radius and volume are all increasing as water is poured into the container. This means that we actually have three things varying with time: the water level \(h\) (the height of the cone of water), the radius \(r\) of the circular top surface of water (the base radius of the cone of water), and the volume of water \(V\). The volume of a cone is given by \( V=\pi r^2h/3\). We know \(dV/dt\), and we want \(dh/dt\). At first something seems to be wrong: we have a third variable \(r\) whose rate we don't know.
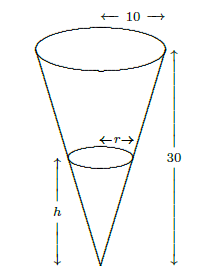
Figure 6.2.2. Conical water tank.
But the dimensions of the cone of water must have the same proportions as those of the container. That is, because of similar triangles, \(r/h=10/30\) so \(r=h/3\). Now we can eliminate \(r\) from the problem entirely: \( V=\pi(h/3)^2h/3=\pi h^3/27\). We take the derivative of both sides and plug in \(h=4\) and \(dV/dt=10\), obtaining \( 10=(3\pi\cdot 4^2/27)(dh/dt)\). Thus, \(dh/dt=90/(16\pi)\) cm/sec.
We have seen that sometimes there are apparently more than two variables that change with time, but in reality there are just two, as the others can be expressed in terms of just two. But sometimes there really are several variables that change with time; as long as you know the rates of change of all but one of them you can find the rate of change of the remaining one. As in the case when there are just two variables, take the derivative of both sides of the equation relating all of the variables, and then substitute all of the known values and solve for the unknown rate.
Notice how this problem differs from example 6.2.2. In both cases we started with the Pythagorean Theorem and took derivatives on both sides. However, in example 6.2.2 one of the sides was a constant (the altitude of the plane), and so the derivative of the square of that side of the triangle was simply zero. In this example, on the other hand, all three sides of the right triangle are variables, even though we are interested in a specific value of each side of the triangle (namely, when the sides have lengths 10 and 15). Make sure that you understand at the start of the problem what are the variables and what are the constants.
Contributors and Attributions
Integrated by Justin Marshall.


