4.3: Maxima and Minima

Learning Objectives

• Define absolute extrema.
• Define local extrema.
• Explain how to find the critical points of a function over a closed interval.
• Describe how to use critical points to locate absolute extrema over a closed interval.

Given a particular function, we are often interested in determining the largest and smallest values of the function. This information is important in creating accurate graphs. Finding the maximum and minimum values of a function also has practical significance, because we can use this method to solve optimization problems, such as maximizing profit, minimizing the amount of material used in manufacturing an aluminum can, or finding the maximum height a rocket can reach. In this section, we look at how to use derivatives to find the largest and smallest values for a function.

Absolute Extrema

Consider the function $f(x)=x^2+1$ over the interval $(−∞,∞)$. As $x→±∞, f(x)→∞$. Therefore, the function does not have a largest value. However, since $x^2+1≥1$ for all real numbers $x$ and $x^2+1=1$ when $x=0$, the function has a smallest value, $1$, when $x=0$. We say that $1$ is the absolute minimum of $f(x)=x^2+1$ and it occurs at $x=0$. We say that $f(x)=x^2+1$ does not have an absolute maximum (Figure $\PageIndex{1}$).

Figure $\PageIndex{1}$: The given function has an absolute minimum of $1$ at $x=0$. The function does not have an absolute maximum.

Definition: Absolute Extrema

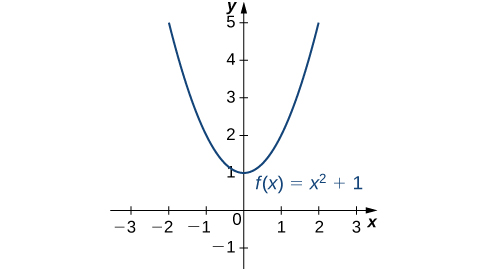
Let $f$ be a function defined over an interval $I$ and let $c∈I$. We say $f$ has an absolute maximum on $I$ at $c$ if $f(c)≥f(x)$ for all $x∈I$. We say $f$ has an absolute minimum on $I$ at $c$ if $f(c)≤f(x)$ for all $x∈I$. If $f$ has an absolute maximum on $I$ at $c$ or an absolute minimum on $I$ at $c$, we say $f$ has an absolute extremum on $I$ at $c$.

Before proceeding, let’s note two important issues regarding this definition. First, the term absolute here does not refer to absolute value. An absolute extremum may be positive, negative, or zero. Second, if a function $f$ has an absolute extremum over an interval $I$ at $c$, the absolute extremum is $f(c)$. The real number $c$ is a point in the domain at which the absolute extremum occurs. For example, consider the function $f(x)=1/(x^2+1)$ over the interval $(−∞,∞)$. Since

$$f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber$$

for all real numbers $x$, we say $f$ has an absolute maximum over $(−∞,∞)$ at $x=0$. The absolute maximum is $f(0)=1$. It occurs at $x=0$, as shown in Figure $\PageIndex{2}$(b).

A function may have both an absolute maximum and an absolute minimum, just one extremum, or neither. Figure $\PageIndex{2}$ shows several functions and some of the different possibilities regarding absolute extrema. However, the following theorem, called the Extreme Value Theorem, guarantees that a continuous function $f$ over a closed, bounded interval $[a,b]$ has both an absolute maximum and an absolute minimum.

Figure $\PageIndex{2}$: Graphs (a), (b), and (c) show several possibilities for absolute extrema for functions with a domain of $(−∞,∞).$ Graphs (d), (e), and (f) show several possibilities for absolute extrema for functions with a domain that is a bounded interval.

Theorem $\PageIndex{1}$: Extreme Value Theorem

If $f$ is a continuous function over the closed, bounded interval $[a,b]$, then there is a point in $[a,b]$ at which $f$ has an absolute maximum over $[a,b]$ and there is a point in $[a,b]$ at which $f$ has an absolute minimum over $[a,b]$.

The proof of the extreme value theorem is beyond the scope of this text. Typically, it is proved in a course on real analysis. There are a couple of key points to note about the statement of this theorem. For the extreme value theorem to apply, the function must be continuous over a closed, bounded interval. If the interval $I$ is open or the function has even one point of discontinuity, the function may not have an absolute maximum or absolute minimum over $I$. For example, consider the functions shown in Figure $\PageIndex{2}$ (d), (e), and (f). All three of these functions are defined over bounded intervals. However, the function in graph (e) is the only one that has both an absolute maximum and an absolute minimum over its domain. The extreme value theorem cannot be applied to the functions in graphs (d) and (f) because neither of these functions is continuous over a closed, bounded interval. Although the function in graph (d) is defined over the closed interval $[0,4]$, the function is discontinuous at $x=2$. The function has an absolute maximum over $[0,4]$ but does not have an absolute minimum. The function in graph (f) is continuous over the half-open interval $[0,2)$, but is not defined at $x=2$, and therefore is not continuous over a closed, bounded interval. The function has an absolute minimum over $[0,2)$, but does not have an absolute maximum over $[0,2)$. These two graphs illustrate why a function over a bounded interval may fail to have an absolute maximum and/or absolute minimum.

Before looking at how to find absolute extrema, let’s examine the related concept of local extrema. This idea is useful in determining where absolute extrema occur.

Local Extrema and Critical Points

Consider the function $f$ shown in Figure $\PageIndex{3}$. The graph can be described as two mountains with a valley in the middle. The absolute maximum value of the function occurs at the higher peak, at $x=2$. However, $x=0$ is also a point of interest. Although $f(0)$ is not the largest value of $f$, the value $f(0)$ is larger than $f(x)$ for all $x$ near 0. We say $f$ has a local maximum at $x=0$. Similarly, the function $f$ does not have an absolute minimum, but it does have a local minimum at $x=1$ because $f(1)$ is less than $f(x)$ for $x$ near 1.

Figure $\PageIndex{3}$: This function $f$ has two local maxima and one local minimum. The local maximum at $x=2$ is also the absolute maximum.

Definition: Local Extrema

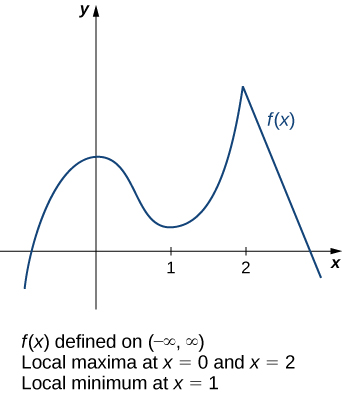
A function $f$ has a local maximum at $c$ if there exists an open interval $I$ containing $c$ such that $I$ is contained in the domain of $f$ and $f(c)≥f(x)$ for all $x∈I$. A function $f$ has a local minimum at $c$ if there exists an open interval $I$ containing $c$ such that $I$ is contained in the domain of $f$ and $f(c)≤f(x)$ for all $x∈I$. A function $f$ has a local extremum at $c$ if $f$ has a local maximum at $c$ or $f$ has a local minimum at $c$.

Note that if $f$ has an absolute extremum at $c$ and $f$ is defined over an interval containing $c$, then $f(c)$ is also considered a local extremum. If an absolute extremum for a function $f$ occurs at an endpoint, we do not consider that to be a local extremum, but instead refer to that as an endpoint extremum.

Given the graph of a function $f$, it is sometimes easy to see where a local maximum or local minimum occurs. However, it is not always easy to see, since the interesting features on the graph of a function may not be visible because they occur at a very small scale. Also, we may not have a graph of the function. In these cases, how can we use a formula for a function to determine where these extrema occur?

To answer this question, let’s look at Figure $\PageIndex{3}$ again. The local extrema occur at $x=0, x=1,$ and $x=2.$ Notice that at $x=0$ and $x=1$, the derivative $f'(x)=0$. At $x=2$, the derivative $f'(x)$ does not exist, since the function $f$ has a corner there. In fact, if $f$ has a local extremum at a point $x=c$, the derivative $f'(c)$ must satisfy one of the following conditions: either $f'(c)=0$ or $f'(c)$ is undefined. Such a value $c$ is known as a critical point and it is important in finding extreme values for functions.

Definition: Critical Points

Let $c$ be an interior point in the domain of $f$. We say that $c$ is a critical point of $f$ if $f'(c)=0$ or $f'(c)$ is undefined.

As mentioned earlier, if $f$ has a local extremum at a point $x=c$, then $c$ must be a critical point of $f$. This fact is known as Fermat’s theorem.

Theorem $\PageIndex{2}$: Fermat’s Theorem

If $f$ has a local extremum at $c$ and $f$ is differentiable at $c$, then $f'(c)=0.$

Proof

Suppose $f$ has a local extremum at $c$ and $f$ is differentiable at $c$. We need to show that $f'(c)=0$. To do this, we will show that $f'(c)≥0$ and $f'(c)≤0$, and therefore $f'(c)=0$. Since $f$ has a local extremum at $c$, $f$ has a local maximum or local minimum at $c$. Suppose $f$ has a local maximum at $c$. The case in which $f$ has a local minimum at $c$ can be handled similarly. There then exists an open interval I such that $f(c)≥f(x)$ for all $x∈I$. Since $f$ is differentiable at $c$, from the definition of the derivative, we know that

$$f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber$$

Since this limit exists, both one-sided limits also exist and equal $f'(c)$. Therefore,

$$f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2}$$

and

$$f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber$$

Since $f(c)$ is a local maximum, we see that $f(x)−f(c)≤0$ for $x$ near $c$. Therefore, for $x$ near $c$, but $x>c$, we have $\frac{f(x)−f(c)}{x−c}≤0$. From Equation $\ref{FermatEqn2}$ we conclude that $f'(c)≤0$. Similarly, it can be shown that $f'(c)≥0.$ Therefore, $f'(c)=0.$

□

From Fermat’s theorem, we conclude that if $f$ has a local extremum at $c$, then either $f'(c)=0$ or $f'(c)$ is undefined. In other words, local extrema can only occur at critical points.

Note this theorem does not claim that a function $f$ must have a local extremum at a critical point. Rather, it states that critical points are candidates for local extrema. For example, consider the function $f(x)=x^3$. We have $f'(x)=3x^2=0$ when $x=0$. Therefore, $x=0$ is a critical point. However, $f(x)=x^3$ is increasing over $(−∞,∞)$, and thus $f$ does not have a local extremum at $x=0$. In Figure $\PageIndex{4}$, we see several different possibilities for critical points. In some of these cases, the functions have local extrema at critical points, whereas in other cases the functions do not. Note that these graphs do not show all possibilities for the behavior of a function at a critical point.

Figure $\PageIndex{4}$: (a–e) A function $f$ has a critical point at $c$ if $f'(c)=0$ or $f'(c)$ is undefined. A function may or may not have a local extremum at a critical point.

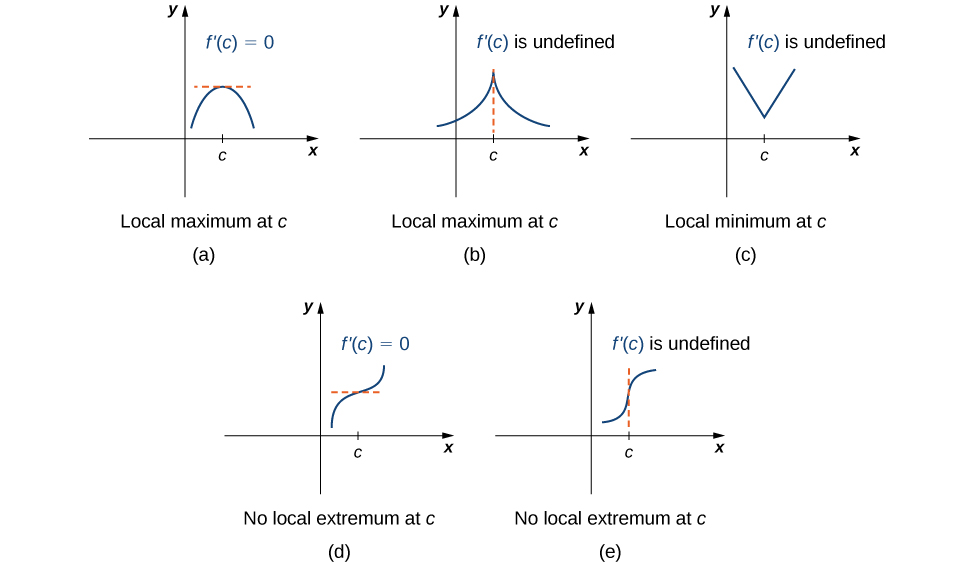
Later in this chapter we look at analytical methods for determining whether a function actually has a local extremum at a critical point. For now, let’s turn our attention to finding critical points. We will use graphical observations to determine whether a critical point is associated with a local extremum.

Example $\PageIndex{1}$: Locating Critical Points

For each of the following functions, find all critical points. Use a graphing utility to determine whether the function has a local extremum at each of the critical points.

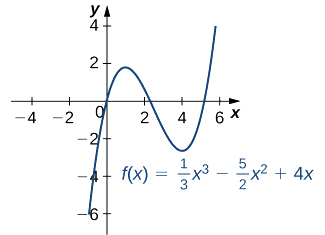
1. $f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x$
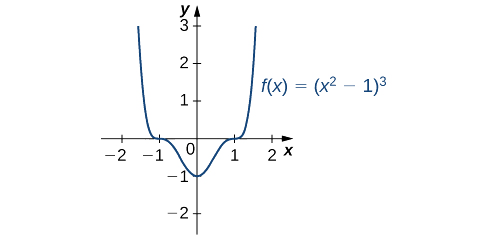
2. $f(x)=(x^2−1)^3$
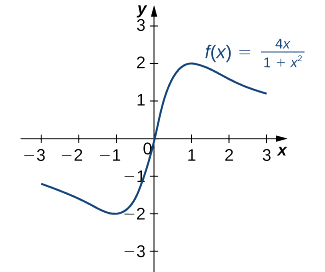
3. $f(x)=\frac{4x}{1+x^2}$

Solution

a. The derivative $f'(x)=x^2−5x+4$ is defined for all real numbers $x$. Therefore, we only need to find the values for $x$ where $f'(x)=0$. Since $f'(x)=x^2−5x+4=(x−4)(x−1)$, the critical points are $x=1$ and $x=4.$ From the graph of $f$ in Figure $\PageIndex{5}$, we see that $f$ has a local maximum at $x=1$ and a local minimum at $x=4$.

Figure $\PageIndex{5}$: This function has a local maximum and a local minimum.

b. Using the chain rule, we see the derivative is

$f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.$

Therefore, $f$ has critical points when $x=0$ and when $x^2−1=0$. We conclude that the critical points are $x=0,±1$. From the graph of $f$ in Figure $\PageIndex{6}$, we see that $f$ has a local (and absolute) minimum at $x=0$, but does not have a local extremum at $x=1$ or $x=−1$.

Figure $\PageIndex{6}$: This function has three critical points: $x=0$, $x=1$, and $x=−1$. The function has a local (and absolute) minimum at $x=0$, but does not have extrema at the other two critical points.

c. By the quotient rule, we see that the derivative is

$f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}$.

The derivative is defined everywhere. Therefore, we only need to find values for $x$ where $f'(x)=0$. Solving $f'(x)=0$, we see that $4−4x^2=0,$ which implies $x=±1$. Therefore, the critical points are $x=±1$. From the graph of $f$ in Figure $\PageIndex{7}$, we see that f has an absolute maximum at $x=1$ and an absolute minimum at $x=−1.$ Hence, $f$ has a local maximum at $x=1$ and a local minimum at $x=−1$. (Note that if $f$ has an absolute extremum over an interval $I$ at a point $c$ that is not an endpoint of $I$, then $f$ has a local extremum at $c.)$

Figure $\PageIndex{7}$: This function has an absolute maximum and an absolute minimum.

Exercise $\PageIndex{1}$

Find all critical points for $f(x)=x^3−\frac{1}{2}x^2−2x+1.$

Hint

Calculate $f'(x).$

Answer

$x=\frac{−2}{3}, x=1$

Locating Absolute Extrema

The extreme value theorem states that a continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum. As shown in Figure $\PageIndex{2}$, one or both of these absolute extrema could occur at an endpoint. If an absolute extremum does not occur at an endpoint, however, it must occur at an interior point, in which case the absolute extremum is a local extremum. Therefore, by Fermat's Theorem, the point $c$ at which the local extremum occurs must be a critical point. We summarize this result in the following theorem.

Theorem $\PageIndex{3}$: Location of Absolute Extrema

Let $f$ be a continuous function over a closed, bounded interval $I$. The absolute maximum of $f$ over $I$ and the absolute minimum of $f$ over $I$ must occur at endpoints of $I$ or at critical points of $f$ in $I$.

With this idea in mind, let’s examine a procedure for locating absolute extrema.

Problem-Solving Strategy: Locating Absolute Extrema over a Closed Interval

Consider a continuous function $f$ defined over the closed interval $[a,b].$

1. Evaluate $f$ at the endpoints $x=a$ and $x=b.$
2. Find all critical points of $f$ that lie over the interval $(a,b)$ and evaluate $f$ at those critical points.
3. Compare all values found in (1) and (2). From "Location of Absolute Extrema," the absolute extrema must occur at endpoints or critical points. Therefore, the largest of these values is the absolute maximum of $f$. The smallest of these values is the absolute minimum of $f$.

Now let’s look at how to use this strategy to find the absolute maximum and absolute minimum values for continuous functions.

Example $\PageIndex{2}$: Locating Absolute Extrema

For each of the following functions, find the absolute maximum and absolute minimum over the specified interval and state where those values occur.

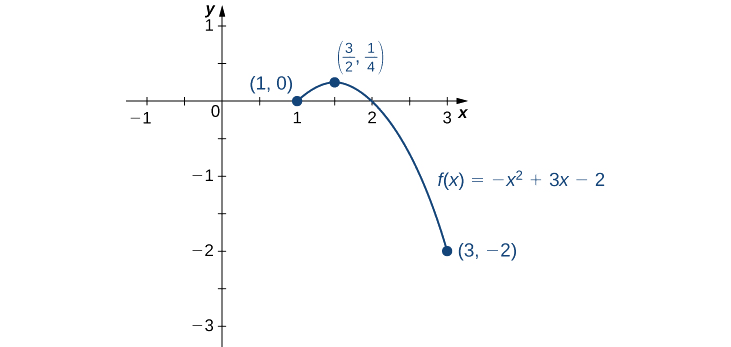
1. $f(x)=−x^2+3x−2$ over $[1,3].$
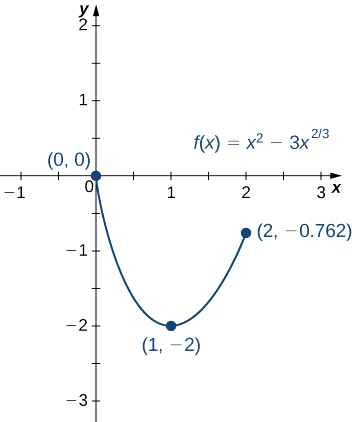
2. $f(x)=x^2−3x^{2/3}$ over $[0,2]$.

Solution

a. Step 1. Evaluate $f$ at the endpoints $x=1$ and $x=3$.

$f(1)=0$ and $f(3)=−2$

Step 2. Since $f'(x)=−2x+3, f'$ is defined for all real numbers $x.$ Therefore, there are no critical points where the derivative is undefined. It remains to check where $f'(x)=0$. Since $f'(x)=−2x+3=0$ at $x=\frac{3}{2}$ and $\frac{3}{2}$ is in the interval $[1,3], f(\frac{3}{2})$ is a candidate for an absolute extremum of $f$ over $[1,3]$. We evaluate $f(\frac{3}{2})$ and find

$f\left(\frac{3}{2}\right)=\frac{1}{4}$.

Step 3. We set up the following table to compare the values found in steps 1 and 2.

$x$	$f(x)$	Conclusion
$1$	$0$
$\frac{3}{2}$	$\frac{1}{4}$	Absolute maximum
$3$	$−2$	Absolute minimum

From the table, we find that the absolute maximum of $f$ over the interval [1, 3] is $\frac{1}{4}$, and it occurs at $x=\frac{3}{2}$. The absolute minimum of $f$ over the interval $[1, 3]$ is $−2$, and it occurs at $x=3$ as shown in Figure $\PageIndex{8}$.

Figure $\PageIndex{8}$: This function has both an absolute maximum and an absolute minimum.

b. Step 1. Evaluate $f$ at the endpoints $x=0$ and $x=2$.

$f(0)=0$ and $f(2)=4−3\left(2\right)^{2/3}≈−0.762$

Step 2. The derivative of $f$ is given by

$f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}$

for $x≠0$. The derivative is zero when $2x^{4/3}−2=0$, which implies $x=±1$. The derivative is undefined at $x=0$. Therefore, the critical points of $f$ are $x=0,1,−1$. The point $x=0$ is an endpoint, so we already evaluated $f(0)$ in step 1. The point $x=−1$ is not in the interval of interest, so we need only evaluate $f(1)$. We find that

$f(1)=−2.$

Step 3. We compare the values found in steps 1 and 2, in the following table.

$x$	$f(x)$	Conclusion
$0$	$0$	Absolute maximum
$1$	$−2$	Absolute minimum
$2$	$−0.762$

We conclude that the absolute maximum of $f$ over the interval $[0, 2]$ is zero, and it occurs at $x=0$. The absolute minimum is $−2,$ and it occurs at $x=1$ as shown in Figure $\PageIndex{9}$.

Figure $\PageIndex{9}$: This function has an absolute maximum at an endpoint of the interval.

Exercise $\PageIndex{2}$

Find the absolute maximum and absolute minimum of $f(x)=x^2−4x+3$ over the interval $[1,4]$.

Hint

Look for critical points. Evaluate $f$ at all critical points and at the endpoints.

Answer

The absolute maximum is $3$ and it occurs at $x=4$. The absolute minimum is $−1$ and it occurs at $x=2$.

At this point, we know how to locate absolute extrema for continuous functions over closed intervals. We have also defined local extrema and determined that if a function $f$ has a local extremum at a point $c$, then $c$ must be a critical point of $f$. However, $c$ being a critical point is not a sufficient condition for $f$ to have a local extremum at $c$. Later in this chapter, we show how to determine whether a function actually has a local extremum at a critical point. First, however, we need to introduce the Mean Value Theorem, which will help as we analyze the behavior of the graph of a function.

Key Concepts

• A function may have both an absolute maximum and an absolute minimum, have just one absolute extremum, or have no absolute maximum or absolute minimum.
• If a function has a local extremum, the point at which it occurs must be a critical point. However, a function need not have a local extremum at a critical point.
• A continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum. Each extremum occurs at a critical point or an endpoint.

Glossary

absolute extremum

if $f$ has an absolute maximum or absolute minimum at $c$, we say $f$ has an absolute extremum at $c$

absolute maximum

if $f(c)≥f(x)$ for all $x$ in the domain of $f$, we say $f$ has an absolute maximum at $c$

absolute minimum

if $f(c)≤f(x)$ for all $x$ in the domain of $f$, we say $f$ has an absolute minimum at $c$

critical point

if $f'(c)=0$ or $f'(c)$ is undefined, we say that c is a critical point of $f$

extreme value theorem

if $f$ is a continuous function over a finite, closed interval, then $f$ has an absolute maximum and an absolute minimum

Fermat’s theorem

if $f$ has a local extremum at $c$, then $c$ is a critical point of $f$

local extremum

if $f$ has a local maximum or local minimum at $c$, we say $f$ has a local extremum at $c$

local maximum

if there exists an interval $I$ such that $f(c)≥f(x)$ for all $x∈I$, we say $f$ has a local maximum at $c$

local minimum

if there exists an interval $I$ such that $f(c)≤f(x)$ for all $x∈I$, we say $f$ has a local minimum at $c$