17.4: Series Solutions of Differential Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Use power series to solve first-order and second-order differential equations.
Previously, we studied how functions can be represented as power series, y(x)=∞∑n=0anxn. We also saw that we can find series representations of the derivatives of such functions by differentiating the power series term by term. This gives
y′(x)=∞∑n=1nanxn−1
and
y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber
In some cases, these power series representations can be used to find solutions to differential equations.
The examples and exercises in this section were chosen for which power solutions exist. However, it is not always the case that power solutions exist. Those of you interested in a more rigorous treatment of this topic should review the differential equations section of the LibreTexts.
- Assume the differential equation has a solution of the form y(x)=\sum_{n=0}^{\infty}a_nx^n. \nonumber
- Differentiate the power series term by term to get y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber andy″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber
- Substitute the power series expressions into the differential equation.
- Re-index sums as necessary to combine terms and simplify the expression.
- Equate coefficients of like powers of x to determine values for the coefficients a_n in the power series.
- Substitute the coefficients back into the power series and write the solution.
Find a power series solution for the following differential equations.
- y''−y=0
- (x^2−1)y″+6xy′+4y=−4
Solution
Part a
Assume
y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1}
Then,
y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2A}
and
y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2B}
We want to find values for the coefficients a_n such that
\begin{align*} &y″−y =0 \\[4pt] &\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}−\sum_{n=0}^{∞}a_nx^n =0 \tag{step 3}. \end{align*}
We want the indices on our sums to match so that we can express them using a single summation. That is, we want to rewrite the first summation so that it starts with n=0.
To re-index the first term, replace n with n+2 inside the sum, and change the lower summation limit to n=0. We get
\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}=\sum_{n=0}^∞ (n+2)(n+1)a_{n+2}x^n. \nonumber
This gives
\begin{align*}\sum_{n=0}^{∞}(n+2)(n+1)a_{n+2}x^n−\sum_{n=0}^{∞}a_nx_n &=0 \\[4pt] \sum_{n=0}^{∞}[(n+2)(n+1)a_{n+2}−a_n]x^n &=0 \tag{step 4}.\end{align*}
Because power series expansions of functions are unique, this equation can be true only if the coefficients of each power of x are zero. So we have
(n+2)(n+1)a_{n+2}−a_n=0 \text{ for }n=0,1,2,…. \nonumber
This recurrence relationship allows us to express each coefficient a_n in terms of the coefficient two terms earlier. This yields one expression for even values of n and another expression for odd values of n. Looking first at the equations involving even values of n, we see that
\begin{align*}a_2 &= \dfrac{a_0}{2} \\[5pt] a_4 &= \dfrac{a_2}{4⋅3} = \dfrac{a_0}{4!}\\[5pt] a_6 &= \dfrac{a_4}{6⋅5} =\dfrac{a_0}{6!} \\ &\qquad ⋮ \end{align*}
Thus, in general, when n is even,
a_n=\dfrac{a_0}{n!}. \tag{step 5}
For the equations involving odd values of n, we see that
\begin{align*}a_3 &=\dfrac{a_1}{3⋅2}=\dfrac{a_1}{3!} \\[5pt] a_5 &= \dfrac{a_3}{5⋅4}=\dfrac{a_1}{5!} \\[5pt] a_7 &= \dfrac{a_5}{7⋅6}=\dfrac{a_1}{7!} \\ &\qquad ⋮ \end{align*}
Therefore, in general, when n is odd,
a_n=\dfrac{a_1}{n!}. \tag{step 5}
Putting this together, we have
\begin{align*}y(x) &= \sum_{n=0}^{∞}a_nx^n \\[4pt] &=a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯. \end{align*}
Re-indexing the sums to account for the even and odd values of n separately, we obtain
y(x)=a_0 \sum_{k=0}^{∞} \dfrac{1}{(2k)!}x^{2k}+a_1 \sum_{k=0}^{∞}\dfrac{1}{(2k+1)!}x^{2k+1}. \tag{step 6}
Analysis for part a.
As expected for a second-order differential equation, this solution depends on two arbitrary constants. However, note that our differential equation is a constant-coefficient differential equation, yet the power series solution does not appear to have the familiar form (containing exponential functions) that we are used to seeing. Furthermore, since y(x)=c_1e^x+c_2e^{−x} is the general solution to this equation, we must be able to write any solution in this form, and it is not clear whether the power series solution we just found can, in fact, be written in that form.
Fortunately, after writing the power series representations of e^x and e^{−x}, and doing some algebra, we find that if we choose
c_0=\dfrac{(a_0+a_1)}{2}, c_1=\dfrac{(a_0−a_1)}{2}, \nonumber
we then have a_0=c_0+c_1 and a_1=c_0−c_1, and
\begin{align*}y(x) &= a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯ \\[4pt] &=(c_0+c_1)+(c_0−c_1)x+\dfrac{(c_0+c_1)}{2}x^2+\dfrac{(c_0−c_1)}{3!}x^3+\dfrac{(c_0+c_1)}{4!}x^4+\dfrac{(c_0−c_1)}{5!}x^5+⋯\\[4pt] &=c_0 \sum_{n=0}^{∞} \dfrac{x^n}{n!}+c_1 \sum_{n=0}^{∞}\dfrac{(−x)^n}{n!} \\[4pt] &=c_0e^x+c_1e^{−x}.\end{align*}
So we have, in fact, found the same general solution. Note that this choice of c_1 and c_2 is not obvious. This is a case when we know what the answer should be, and have essentially “reverse-engineered” our choice of coefficients.
Part b
Assume
y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1}
Then,
y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2}
and
y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2}
We want to find values for the coefficients a_n such that
\begin{align*}(x^2−1)y″+6xy′+4y &=−4 \\ (x^2−1) \sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4 \\[4pt] x^2 \sum_{n=2}^{∞} n(n−1)a_nx^{n−2}−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4. \end{align*}
Taking the external factors inside the summations, we get
\sum_{n=2}^{∞}n(n−1)a_nx^n−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+\sum_{n=1}^∞ 6na_nx^n+ \sum_{n=0}^∞ 4a_nx^n=−4 \tag{step 3}.
Now, in the first summation, we see that when n=0 or n=1, the term evaluates to zero, so we can add these terms back into our sum to get
\sum_{n=2}^{∞}n(n−1)a_nx^n=\sum_{n=0}^∞ n(n−1)a_nx^n. \nonumber
Similarly, in the third term, we see that when n=0, the expression evaluates to zero, so we can add that term back in as well. We have
\sum_{n=1}^∞ 6na_nx^n=\sum_{n=0}^∞6na_nx^n. \nonumber
Then, we need only shift the indices in our second term. We get
\sum_{n=2}^∞n(n−1)a_nx^{n−2}=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n. \nonumber
Thus, we have
\begin{align*} \sum_{n=0}^∞n(n−1)a_nx^n−\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n+\sum_{n=0}^∞6na_nx^n+\sum_{n=0}^∞4a_nx^n &=−4 \tag{step 4} \\[4pt] \sum_{n=0}^∞[n(n−1)a_n−(n+2)(n+1)a_{n+2}+6na_n+4a_n]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n^2−n)a_n+6na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[n^2a_n+5na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞ [(n^2+5n+4)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \end{align*}
Looking at the coefficients of each power of x, we see that the constant term must be equal to −4, and the coefficients of all other powers of x must be zero. Then, looking first at the constant term,
\begin{aligned}4a_0−2a_2 &=−4 \\ a_2 &=2a_0+2 \end{aligned} \tag{step 3}
For n≥1, we have
\begin{align*}(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2} &= 0 \\[4pt] (n+1)[(n+4)a_n−(n+2)a_{n+2}] &=0. \end{align*}
Since n≥1, \; n+1≠0, we see that
(n+4)a_n−(n+2)a_{n+2}=0 \nonumber
and thus
a_{n+2}=\dfrac{n+4}{n+2}a_n. \nonumber
For even values of n, we have
\begin{align*} a_4 &=\dfrac{6}{4}(2a_0+2)=3a_0+3 \\ a_6 &= \dfrac{8}{6}(3a_0+3)=4a_0+4 \\[4pt] &\qquad ⋮ \end{align*}
In general,
a_{2k}=(k+1)(a_0+1). \tag{step 5}
For odd values of n, we have
\begin{align*}a_3 &=\dfrac{5}{3}a_1 \\[4pt] a_5 &= \dfrac{7}{5}a_3=\dfrac{7}{3}a_1 \\[4pt] a_7 &=\dfrac{9}{7}a_5=\dfrac{9}{3} a_1=3a_1 \\[4pt] &\qquad ⋮ \end{align*}
In general,
a_{2k+1}=\dfrac{2k+3}{3}a_1. \tag{step 5 continued}
Putting this together, we have
y(x)=\sum_{k=0}^∞ (k+1)(a_0+1)x^{2k}+\sum_{k=0}^∞ (\dfrac{2k+3}{3})a_1x^{2k+1}. \tag{step 6}
Find a power series solution for the following differential equations.
- y′+2xy=0
- (x+1)y′=3y
- Hint
-
Follow the problem-solving strategy.
- Answer a
-
\displaystyle y(x)=a_0 \sum_{n=0}^∞ \dfrac{(−1)^n}{n!}x^{2n}=a_0e^{−x^2}
- Answer b
-
y(x)=a_0(x+1)^3
Bessel functions
We close this section with a brief introduction to Bessel functions. Complete treatment of Bessel functions is well beyond the scope of this course, but we get a little taste of the topic here so we can see how series solutions to differential equations are used in real-world applications. The Bessel equation of order n is given by
x^2y″+xy′+(x^2−n^2)y=0. \nonumber
This equation arises in many physical applications, particularly those involving cylindrical coordinates, such as the vibration of a circular drum head and transient heating or cooling of a cylinder. In the next example, we find a power series solution to the Bessel equation of order 0.
Find a power series solution to the Bessel equation of order 0 and graph the solution.
Solution
The Bessel equation of order 0 is given by
x^2y″+xy′+x^2y=0. \nonumber
We assume a solution of the form \displaystyle y=\sum_{n=0}^∞ a_nx^n. Then \displaystyle y′(x)=\sum_{n=1}^∞ na_nx^{n−1} and \displaystyle y''(x)=\sum_{n=2}^∞n(n−1)a_nx^{n−2}.Substituting this into the differential equation, we get
\begin{align*} x^2 \sum_{n=2}^∞ n(n−1)a_nx^{n−2}+x \sum_{n=1}^∞ na_nx^{n−1}+x^2 \sum_{n=0}^∞ a_nx^n&=0 & & \text{Substitution.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+ \sum_{n=0}^∞ a_nx^{n+2}&=0 & & \text{Bring external factors within sums.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Re-index third sum.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+a_1x+\sum_{n=2}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Separate }n=1 \text{ term from second sum.} \\[5pt] a_1x+\sum_{n=2}^∞ [n(n−1)a_n+na_n+a_{n−2}]x^n&=0 & & \text{Collect summation terms.} \\[5pt] a_1x+\sum_{n=2}^∞ [(n^2−n)a_n+na_n+a_{n−2}]x^n &=0 & & \text{Multiply through in first term.} \\[5pt] a_1x+\sum_{n=2}^∞ [n^2a_n+a_{n−2}]x^n &=0. & & \text{Simplify.} \end{align*}
Then, a_1=0, and for n≥2,
\begin{align*} n^2a_n+a_{n−2} &= 0 \\[4pt] a_n&=−\dfrac{1}{n^2}a_{n−2}. \end{align*} \nonumber
Because a_1=0, all odd terms are zero. Then, for even values of n, we have
\begin{align*}a_2 &=−\dfrac{1}{2^2}a_0 \\[4pt] a_4 &= −\dfrac{1}{4^2}a_2=\dfrac{1}{4^2⋅2^2} a_0. \\[4pt] a_6 &=−\dfrac{1}{6^2}a_4 =−\dfrac{1}{6^2⋅4^2⋅2^2}a_0 \end{align*}
In general,
a_{2k}=\dfrac{(−1)^k}{(2)^{2k}(k!)^2}a_0. \nonumber
Thus, we have
y(x)=a_0 \sum_{k=0}^∞ \dfrac{(−1)^k}{(2)^{2k}(k!)^2}x^{2k}. \nonumber
The graph appears below.
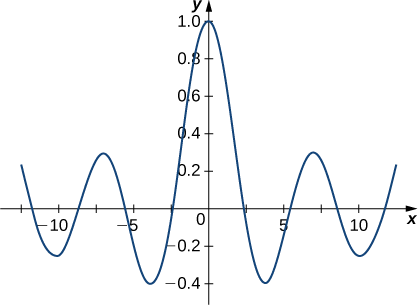
Verify that the expression found in Example \PageIndex{2} is a solution to the Bessel equation of order 0.
- Hint
-
Differentiate the power series term by term and substitute it into the differential equation.
Key Concepts
- Power series representations of functions can sometimes be used to find solutions to differential equations.
- Differentiate the power series term by term and substitute into the differential equation to find relationships between the power series coefficients.

