9.9: Arc Length
- Page ID
- 483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Here is another geometric application of the integral: find the length of a portion of a curve. As usual, we need to think about how we might approximate the length, and turn the approximation into an integral.
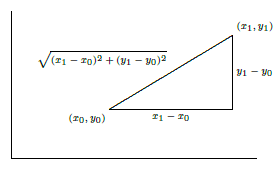
We already know how to compute one simple arc length, that of a line segment. If the endpoints are \( P_0(x_0,y_0)\) and \( P_1(x_1,y_1)\) then the length of the segment is the distance between the points, \( \sqrt{(x_1-x_0)^2+(y_1-y_0)^2}\), from the Pythagorean theorem, as illustrated in Figure \( \PageIndex{1}\).
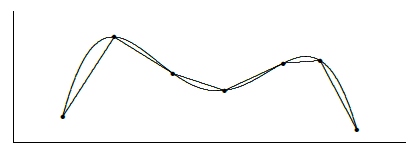
Now if the graph of \(f\) is "nice'' (say, differentiable) it appears that we can approximate the length of a portion of the curve with line segments, and that as the number of segments increases, and their lengths decrease, the sum of the lengths of the line segments will approach the true arc length; see Figure \( \PageIndex{2}\).
Now we need to write a formula for the sum of the lengths of the line segments, in a form that we know becomes an integral in the limit. So we suppose we have divided the interval \([a,b]\) into \(n\) subintervals as usual, each with length \(\Delta x =(b-a)/n\), and endpoints \( a=x_0\), \( x_1\), \( x_2\), …, \( x_n=b\). The length of a typical line segment, joining \( (x_i,f(x_i))\) to \( (x_{i+1},f(x_{i+1}))\), is \(\sqrt{(\Delta x )^2 +(f(x_{i+1})-f(x_i))^2}\). By the Mean Value Theorem (6.5.2), there is a number \( t_i\) in \( (x_i,x_{i+1})\) such that \( f'(t_i)\Delta x=f(x_{i+1})-f(x_i)\), so the length of the line segment can be written as
\[ \sqrt{(\Delta x)^2 + (f'(t_i))^2\Delta x^2}= \sqrt{1+(f'(t_i))^2}\,\Delta x. \]
The arc length is then
\[ \lim_{n\to\infty}\sum_{i=0}^{n-1} \sqrt{1+(f'(t_i))^2}\,\Delta x= \int_a^b \sqrt{1+(f'(x))^2}\,dx. \]
Note that the sum looks a bit different than others we have encountered, because the approximation contains a \( t_i\) instead of an \( x_i\). In the past we have always used left endpoints (namely, \( x_i\)) to get a representative value of \(f\) on \( [x_i,x_{i+1}]\); now we are using a different point, but the principle is the same.
To summarize, to compute the length of a curve on the interval \([a,b]\), we compute the integral
\[\int_a^b \sqrt{1+(f'(x))^2}\,dx.\]
Unfortunately, integrals of this form are typically difficult or impossible to compute exactly, because usually none of our methods for finding antiderivatives will work. In practice this means that the integral will usually have to be approximated.
Example \( \PageIndex{1}\)
Let \( f(x) = \sqrt{r^2-x^2}\), the upper half circle of radius \(r\). The length of this curve is half the circumference, namely \(\pi r\). Let's compute this with the arc length formula.
Solution
The derivative \(f'\) is \( -x/\sqrt{r^2-x^2}\) so the integral is
\[ \int_{-r}^r \sqrt{1+{x^2\over r^2-x^2}}\,dx =\int_{-r}^r \sqrt{r^2\over r^2-x^2}\,dx =r\int_{-r}^r \sqrt{1\over r^2-x^2}\,dx. \]
Using a trigonometric substitution, we find the antiderivative, namely \( \arcsin(x/r)\). Notice that the integral is improper at both endpoints, as the function \( \sqrt{1/(r^2-x^2)}\) is undefined when \(x=\pm r\). So we need to compute
\[ \lim_{D\to-r^+}\int_D^0 \sqrt{1\over r^2-x^2}\,dx + \lim_{D\to r^-}\int_0^D \sqrt{1\over r^2-x^2}\,dx. \]
This is not difficult, and has value \(\pi\), so the original integral, with the extra \(r\) in front, has value \(\pi r\) as expected.


