7.3.1: Boundary Value Problems: Dirichlet Problem
- Page ID
- 2186
The Dirichlet problem (first boundary value problem) is to find a solution \(u\in C^2(\Omega)\cap C(\overline{\Omega})\) of
\begin{eqnarray}
\label{D1}\tag{7.3.1.1}
\triangle u&=&0\ \ \mbox{in}\ \Omega\\
\label{D2}\tag{7.3.1.2}
u&=&\Phi\ \ \mbox{on}\ \partial\Omega,
\end{eqnarray}
where \(\Phi\) is given and continuous on \(\partial\Omega\).
Proposition 7.4. Assume \(\Omega\) is bounded, then a solution to the Dirichlet problem is uniquely determined.
Proof. Maximum principle.
Remark. The previous result fails if we take away in the boundary condition (\ref{D2}) one point from the the boundary as the following example shows. Let \(\Omega\subset\mathbb{R}^2\) be the domain
$$
\Omega=\{x\in B_1(0):\ x_2>0\},
\]
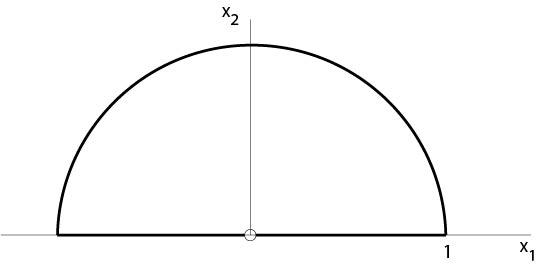
Figure 7.3.1.1: Counterexample
Assume \(u\in C^2(\Omega)\cap C(\overline{\Omega}\setminus\{0\})\) is a solution of
\begin{eqnarray*}
\triangle u&=&0\ \ \mbox{in}\ \Omega\\
u&=&0\ \ \mbox{on}\ \partial\Omega\setminus\{0\}.
\end{eqnarray*}
This problem has solutions \(u\equiv 0\) and \(u=\mbox{Im}(z+z^{-1})\), where \(z=x_1+ix_2\). Concerning another example see an exercise.
In contrast to this behavior of the Laplace equation, one has uniqueness if $\triangle u=0$ is replaced by the minimal surface equation
$$
\frac{\partial}{\partial x_1}\left(\frac{u_{x_1}}{\sqrt{1+|\nabla u|^2}}\right)+
\frac{\partial}{\partial x_2}\left(\frac{u_{x_2}}{\sqrt{1+|\nabla u|^2}}\right)=0.
\]
Contributors and Attributions
Integrated by Justin Marshall.


