10.1: Temperature on a Disk
( \newcommand{\kernel}{\mathrm{null}\,}\)
Let us now turn to a different two-dimensional problem. A circular disk is prepared in such a way that its initial temperature is radially symmetric, u(ρ,ϕ,t=0)=f(ρ). Then it is placed between two perfect insulators and its circumference is connected to a freezer that keeps it at 0∘ C, as sketched in Fig. 10.1.2.
Figure 10.1.1: A circular plate, insulated from above and below.
Since the initial conditions do not depend on ϕ, we expect the solution to be radially symmetric as well, u(ρ,t), which satisfies the equation ∂u∂t=k[∂2u∂ρ2+1ρ∂u∂ρ],u(c,t)=0,u(ρ,0)=f(ρ).
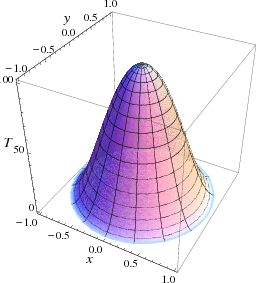
Figure 10.1.2: The initial temperature in the disk.
Once again we separate variables, u(ρ,t)=R(ρ)T(t), which leads to the equation
1kT′T=R″ This corresponds to the two equations
\begin{aligned} \rho^2 R''+\rho R' + \lambda \rho^2 R &= 0,\quad R(c)=0m\nonumber\\ T'+\lambda k T = 0.\end{aligned} \nonumber
The radial equation (which has a regular singular point at \rho=0) is closely related to one of the most important equation of mathematical physics, Bessel’s equation. This equation can be reached from the substitution \rho = x /\sqrt{\lambda}, so that with R(r)=X(x) we get the equation
x^2 \frac{d^2}{dx^2} X(x) + x \frac{d}{dx} X(x) + x^2 X(x) = 0, \qquad X(\sqrt \lambda c) =0. \nonumber


