10.4: Multiply Polynomials (Part 1)
- Page ID
- 7253
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Multiply a polynomial by a monomial
- Multiply a binomial by a binomial
- Multiply a trinomial by a binomial
Before you get started, take this readiness quiz.
- Distribute: 2(x + 3). If you missed the problem, review Example 7.4.1.
- Distribute: −11(4 − 3a). If you missed the problem, review Example 7.4.10.
- Combine like terms: x2 + 9x + 7x + 63. If you missed the problem, review Example 2.3.9.
Multiply a Polynomial by a Monomial
In Distributive Property you learned to use the Distributive Property to simplify expressions such as 2(x − 3). You multiplied both terms in the parentheses, x and 3, by 2, to get 2x − 6. With this chapter's new vocabulary, you can say you were multiplying a binomial, x − 3, by a monomial, 2. Multiplying a binomial by a monomial is nothing new for you!
Multiply: 3(x + 7).
Solution
| Distribute. | 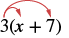 |
| 3 • x + 3 • 7 | |
| Simplify. | 3x + 21 |
Multiply: 6(x + 8).
- Answer
-
6x + 48
Multiply: 2(y + 12).
- Answer
-
2y + 24
Multiply: x(x − 8).
Solution
| Distribute. | 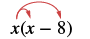 |
| x2 - 8x | |
| Simplify. | x2 - 8x |
Multiply: y(y − 9).
- Answer
-
\( y^{2}-9 y\)
Multiply: p(p − 13).
- Answer
-
\( p^2 - 13p\)
Multiply: 10x(4x + y).
Solution
| Distribute. | 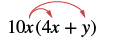 |
| 10x • 4x + 10x • y | |
| Simplify. | 40x2 + 10xy |
Multiply: 8x(x + 3y).
- Answer
-
\(8x^2+24xy \)
Multiply: 3r(6r + s).
- Answer
-
\(18r^2+3rs \)
Multiplying a monomial by a trinomial works in much the same way.
Multiply: −2x(5x2 + 7x − 3).
Solution
| Distribute. |  |
| -2x • 5x2 + (-2x) • 7x - (-2x) • 3 | |
| Simplify. | -10x3 -14x2 + 6x |
Multiply: −4y(8y2 + 5y − 9).
- Answer
-
\(-32y^3-20y^2+36y \)
Multiply: −6x(9x2 + x − 1).
- Answer
-
\( -54x^3-6x^2+6x\)
Multiply: 4y3(y2 − 8y + 1).
Solution
| Distribute. | 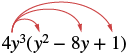 |
| 4y3 • y2 - 4y3 • 8y + 4y3 • 1 | |
| Simplify. | 4y5 -32y4 + 4y3 |
Multiply: 3x2 (4x2 − 3x + 9).
- Answer
-
\( 12 x^{4}-9 x^{3}+27 x^{2}\)
Multiply: 8y2 (3y2 − 2y − 4).
- Answer
-
\(24 y^{4}-16 y^{3}-32 y^{2} \)
Now we will have the monomial as the second factor.
Multiply: (x + 3)p.
Solution
| Distribute. | 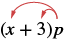 |
| x • p + 3 • p | |
| Simplify. | xp + 3p |
Multiply: (x + 8)p.
- Answer
-
\(xp+8p \)
Multiply: (a + 4)p.
- Answer
-
\(ap + 4p \)
Multiply a Binomial by a Binomial
Just like there are different ways to represent multiplication of numbers, there are several methods that can be used to multiply a binomial times a binomial.
Using the Distributive Property
We will start by using the Distributive Property. Look again at Example \(\PageIndex{6}\).
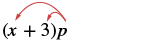 |
|
| We distributed the p to get |  |
| What if we have (x + 7) instead of p? Think of the (x + 7) as the \(\textcolor{red}{p}\) above. | 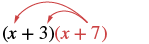 |
| Distribute (x + 7). | 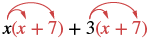 |
| Distribute again. | x2 + 7x + 3x + 21 |
| Combine like terms. | x2 + 10x + 21 |
Notice that before combining like terms, we had four terms. We multiplied the two terms of the first binomial by the two terms of the second binomial—four multiplications.
Be careful to distinguish between a sum and a product.
\[\begin{split} &\textbf{Sum} \qquad \qquad \qquad \quad \textbf{Product} \\ &x + x \qquad \qquad \qquad \qquad x \cdot x \\ &\; \; 2x \qquad \qquad \qquad \qquad \qquad x^{2} \\ combine\; &like\; terms \qquad add\; exponents\; of\; like\; bases \end{split}\]
Multiply: (x + 6)(x + 8).
Solution
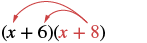 |
|
| Distribute (x + 8). | 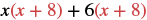 |
| Distribute again. | x2 + 8x + 6x + 48 |
| Simplify. | x2 + 14x + 48 |
Multiply: (x + 8)(x + 9).
- Answer
-
\(x^{2}+17 x+72 \)
Multiply: (a + 4)(a + 5).
- Answer
-
\(a^{2}+9 a+20 \)
Now we'll see how to multiply binomials where the variable has a coefficient.
Multiply: (2x + 9)(3x + 4).
Solution
| Distribute (3x + 4). | 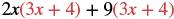 |
| Distribute again. | 6x2 + 8x + 27x + 36 |
| Simplify. | 6x2 + 35x + 36 |
Multiply: (5x + 9)(4x + 3).
- Answer
-
\(20 x^{2}+51 x+27 \)
Multiply: (10m + 9)(8m + 7).
- Answer
-
\(80 m^{2}+142 m+63 \)
In the previous examples, the binomials were sums. When there are differences, we pay special attention to make sure the signs of the product are correct.
Multiply: (4y + 3)(6y − 5).
Solution
| Distribute. | 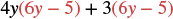 |
| Distribute again. | 24y2 − 20y + 18y − 15 |
| Simplify. | 24y2 − 2y − 15 |
Multiply: (7y + 1)(8y − 3).
- Answer
-
\( 56 y^{2}-13 y-3\)
Multiply: (3x + 2)(5x − 8).
- Answer
-
\(15 x^{2}-14 x-16 \)
Up to this point, the product of two binomials has been a trinomial. This is not always the case.
Multiply: (x + 2)(x − y).
Solution
| Distribute. | 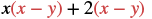 |
| Distribute again. | x2 - xy + 2x - 2y |
| Simplify. | There are no like terms to combine. |
Multiply: (x + 5)(x − y).
- Answer
-
\( x^{2}-x y+5 x-5 y\)
Multiply: (x + 2y)(x − 1).
- Answer
-
\( x^{2}-x+2 x y-2 y\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


