12.E: Introduction to Calculus (Exercises)
- Page ID
- 7390
12.1: Finding Limits - Numerical and Graphical Approaches
In this section, we will examine numerical and graphical approaches to identifying limits.
Verbal
1) Explain the difference between a value at \(x=a\) and the limit as \(x\) approaches \(a\).
- Answer
-
The value of the function, the output, at \(x=a\) is \(f(a)\). When the \(\lim \limits_{x \to a}f(x)\) is taken, the values of \(x\) get infinitely close to \(a\) but never equal \(a\). As the values of \(x\) approach \(a\) from the left and right, the limit is the value that the function is approaching.
2) Explain why we say a function does not have a limit as \(x\) approaches \(a\) if, as \(x\) approaches \(a\), the left-hand limit is not equal to the right-hand limit.
Graphical
For the exercises 3-14, estimate the functional values and the limits from the graph of the function \(f\) provided in the Figure below.
3) \(\lim \limits_{x \to −2^−} f(x)\)
- Answer
-
\(-4\)
4) \(\lim \limits_{x \to −2^+ }f(x)\)
5) \(\lim \limits_{x \to −2 f(x)}\)
- Answer
-
\(-4\)
6) \(f(−2)\)
7) \(\lim \limits_{x \to −1^− f(x)}\)
- Answer
-
\(2\)
8) \(\lim \limits_{x \to 1^+} f(x)\)
9) \(\lim \limits_{x \to 1} f(x)\)
- Answer
-
does not exist
10) \(f(1)\)
11) \(\lim \limits_{x \to 4^−} f(x)\)
- Answer
-
\(4\)
12) \(\lim \limits_{x \to 4^+} f(x)\)
13) \(\lim \limits_{x \to 4} f(x)\)
- Answer
-
does not exist
14) \(f(4)\)
For the exercises 15-21, draw the graph of a function from the functional values and limits provided.
15) \(\lim \limits_{x \to 0^−} f(x)=2, \lim \limits_{x \to 0^+} f(x)=–3, \lim \limits_{x \to 2} f(x)=2, f(0)=4, f(2)=–1, f(–3) \text{ does not exist.}\)
- Answer
-
Answers will vary.
16) \(\lim \limits_{x \to 2^−} f(x)=0,\lim \limits_{x \to 2^+} =–2,\lim \limits_{x \to 0} f(x)=3, f(2)=5, f(0)\)
- Answer
-
Answers will vary.
17) \(\lim \limits_{ x \to 2^−} f(x)=2, \lim \limits_{ x \to 2^+} f(x)=−3, \lim \limits_{x \to 0} f(x)=5, f(0)=1, f(1)=0\)
- Answer
-
Answers will vary.
18) \(\lim \limits_{x \to 3^−} f(x)=0, \lim \limits_{x \to 3^+} f(x)=5, \lim \limits_{x \to 5} f(x)=0, f(5)=4, f(3) \text{ does not exist.}\)
- Answer
-
Answers will vary.
19) \( \lim \limits_{ x \to 4} f(x)=6, \lim \limits_{ x \to 6^+} f(x)=−1, \lim \limits_{ x \to 0} f(x)=5, f(4)=6, f(2)=6\)
- Answer
-
Answers will vary.
20) \( \lim \limits_{ x \to −3} f(x)=2, \lim \limits_{ x \to 1^+} f(x)=−2, \lim \limits_{ x \to 3} f(x)=–4, f(–3)=0, f(0)=0\)
- Answer
-
Answers will vary.
21) \( \lim \limits_{ x \to π} f(x)=π^2, \lim \limits_{ x \to –π} f(x)=\dfrac{π}{2}, \lim \limits_{ x \to 1^-} f(x)=0, f(π)=\sqrt{2}, f(0) \text{ does not exist}.\)
- Answer
-
Answers will vary.
For the exercises 22-26, use a graphing calculator to determine the limit to \(5\) decimal places as \(x\) approaches \(0\).
22) \(f(x)=(1+x)^{\frac{1}{x}}\)
23) \(g(x)=(1+x)^{\frac{2}{x}}\)
- Answer
-
\(7.38906\)
24) \(h(x)=(1+x)^{\frac{3}{x}}\)
25) \(i(x)=(1+x)^{\frac{4}{x}}\)
- Answer
-
\(54.59815\)
26) \(j(x)=(1+x)^{\frac{5}{x}}\)
27) Based on the pattern you observed in the exercises above, make a conjecture as to the limit of \(f(x)=(1+x)^{\frac{6}{x}}, g(x)=(1+x)^{\frac{7}{x}},\) and \(h(x)=(1+x)^{\frac{n}{x}}.\)
- Answer
-
\(e^6≈403.428794,e^7≈1096.633158, e^n\)
For the exercises 28-29, use a graphing utility to find graphical evidence to determine the left- and right-hand limits of the function given as \(x\) approaches \(a\). If the function has a limit as \(x\) approaches \(a\),state it. If not, discuss why there is no limit.
28) \((x)= \begin{cases} |x|−1, && \text{if }x≠1 \\ x^3, && \text{if }x=1 \end{cases} a=1 \)
29) \((x)= \begin{cases} \frac{1}{x+1}, && \text{if } x=−2 \\ (x+1)^2, && \text{if } x≠−2 \end{cases} a=−2 \)
- Answer
-
\(\lim \limits_{x \to −2} f(x)=1\)
Numeric
For the exercises 30-38, use numerical evidence to determine whether the limit exists at \(x=a\). If not, describe the behavior of the graph of the function near \(x=a\). Round answers to two decimal places.
30) \(f(x)=\dfrac{x^2−4x}{16−x^2};a=4\)
31) \(f(x)=\dfrac{x^2−x−6}{x^2−9};a=3\)
- Answer
-
\(\lim \limits_{x \to 3} \left (\dfrac{x^2−x−6}{x^2−9} \right )=\dfrac{5}{6}≈0.83\)
32) \(f(x)=\dfrac{x^2−6x−7}{x^2– 7x};a=7\)
33) \(f(x)=\dfrac{x^2–1}{x^2–3x+2};a=1\)
- Answer
-
\(\lim \limits_{x \to 1} \left (\dfrac{x^2−1}{x^2−3x+2} \right )=−2.00\)
34) \(f(x)=\dfrac{1−x^2}{x^2−3x+2};a=1\)
35) \(f(x)=\dfrac{10−10x^2}{x^2−3x+2};a=1\)
- Answer
-
\(\lim \limits_{x \to 1} \left (\dfrac{10−10x^2}{x^2−3x+2} \right )=20.00\)
36) \(f(x)=\dfrac{x}{6x^2−5x−6};a=\dfrac{3}{2}\)
37) \(f(x)=\dfrac{x}{4x^2+4x+1};a=−\dfrac{1}{2}\)
- Answer
-
\(\lim \limits_{x \to \frac{−1}{2}} \left (\dfrac{x}{4x^2+4x+1} \right )\) does not exist. Function values decrease without bound as \(x\) approaches \(-0.5\) from either left or right.
38) \(f(x)=\frac{2}{x−4}; a=4\)
For the exercises 39-41, use a calculator to estimate the limit by preparing a table of values. If there is no limit, describe the behavior of the function as \(x\) approaches the given value.
39) \(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}\)
- Answer
-
\(\lim \limits_{x \to 0} \dfrac{7 \tan x}{3x}=\dfrac{7}{3}\)

40) \(\lim \limits_{x \to 4} \dfrac{x^2}{x−4}\)
- Answer
-

41) \(\lim \limits_{x \to 0}\dfrac{2 \sin x}{4 \tan x}\)
- Answer
-
\(\lim \limits_{x \to 0} \dfrac{2 \sin x}{4 \tan x}=\dfrac{1}{2}\)

For the exercises 42-49, use a graphing utility to find numerical or graphical evidence to determine the left and right-hand limits of the function given as \(x\) approaches \(a\). If the function has a limit as \(x\) approaches \(a\), state it. If not, discuss why there is no limit.
42) \(\lim \limits_{x \to 0}e^{e^{\frac{1}{x}}}\)
43) \(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}\)
- Answer
-
\(\lim \limits_{x \to 0}e^{e^{− \frac{1}{x^2}}}=1.0\)
44) \(\lim \limits_{x \to 0} \dfrac{|x|}{x}\)
45) \(\lim \limits_{x \to −1} \dfrac{|x+1|}{x+1}\)
- Answer
-
\(\lim \limits_{ x→−1^−}\dfrac{| x+1 |}{x+1}=\dfrac{−(x+1)}{(x+1)}=−1\) and \(\lim \limits_{ x \to −1^+}\dfrac{| x+1 |}{x+1}=\dfrac{(x+1)}{(x+1)}=1\); since the right-hand limit does not equal the left-hand limit, \(\lim \limits_{ x \to −1}\dfrac{|x+1|}{x+1}\) does not exist.
46) \(\lim \limits_{ x \to 5} \dfrac{| x−5 |}{5−x}\)
47) \(\lim \limits_{ x \to −1}\dfrac{1}{(x+1)^2}\)
- Answer
-
\(\lim \limits_{ x \to −1} \dfrac{1}{(x+1)^2}\) does not exist. The function increases without bound as \(x\) approaches \(−1\) from either side.
48) \(\lim \limits_{ x \to 1} \dfrac{1}{(x−1)^3}\)
49) \(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\)
- Answer
-
\(\lim \limits_{ x \to 0} \dfrac{5}{1−e^{\frac{2}{x}}}\) does not exist. Function values approach \(5\) from the left and approach \(0\) from the right.
50) Use numerical and graphical evidence to compare and contrast the limits of two functions whose formulas appear similar: \(f(x)=\left | \dfrac{1−x}{x} \right |\) and \(g(x)=\left | \dfrac{1+x}{x} \right |\) as \(x\) approaches \(0\). Use a graphing utility, if possible, to determine the left- and right-hand limits of the functions \(f(x)\) and \(g(x)\) as \(x\) approaches \(0\). If the functions have a limit as \(x\) approaches \(0\), state it. If not, discuss why there is no limit.
Extensions
51) According to the Theory of Relativity, the mass m m of a particle depends on its velocity \(v\). That is
\[m=\dfrac{m_o}{\sqrt{1−(v^2/c^2)}} \nonumber \]
where \(m_o\) is the mass when the particle is at rest and \(c\) is the speed of light. Find the limit of the mass, \(m\), as \(v\) approaches \(c^−.\)
- Answer
-
Through examination of the postulates and an understanding of relativistic physics, as \(v→c, m→∞. \)Take this one step further to the solution, \[\lim \limits_{v \to c^−}m=\lim \limits_{v \to c^−} \dfrac{m_o}{\sqrt{1−(v^2/c^2)}}=∞ \nonumber \]
52) Allow the speed of light, \(c\), to be equal to \(1.0\). If the mass, \(m\), is \(1\), what occurs to \(m\) as \(v \to c\)? Using the values listed in the Table below, make a conjecture as to what the mass is as \(v\) approaches \(1.00\).
| \(v\) | \(m\) |
|---|---|
| 0.5 | 1.15 |
| 0.9 | 2.29 |
| 0.95 | 3.20 |
| 0.99 | 7.09 |
| 0.999 | 22.36 |
| 0.99999 | 223.61 |
12.2: Finding Limits - Properties of Limits
Graphing a function or exploring a table of values to determine a limit can be cumbersome and time-consuming. When possible, it is more efficient to use the properties of limits, which is a collection of theorems for finding limits. Knowing the properties of limits allows us to compute limits directly.
Verbal
1) Give an example of a type of function \(f\) whose limit, as \(x\) approaches \(a,\) is \(f(a)\).
- Answer
-
If \(f\) is a polynomial function, the limit of a polynomial function as \(x\) approaches \(a\) will always be \(f(a)\).
2) When direct substitution is used to evaluate the limit of a rational function as \(x\) approaches \(a\) and the result is \(f(a)=\dfrac{0}{0}\),does this mean that the limit of \(f\) does not exist?
3) What does it mean to say the limit of \(f(x)\), as \(x\) approaches \(c\), is undefined?
- Answer
-
It could mean either (1) the values of the function increase or decrease without bound as \(x\) approaches \(c,\) or (2) the left and right-hand limits are not equal.
Algebraic
For the exercises 4-30, evaluate the limits algebraically.
4) \(\lim \limits_{x \to 0} (3)\)
5) \(\lim \limits_{x \to 2} \left (\dfrac{−5x}{x^2−1} \right )\)
- Answer
-
\(\dfrac{−10}{3}\)
6) \(\lim \limits_{x \to 2} \left (\dfrac{x^2−5x+6}{x+2} \right )\)
7) \(\lim \limits_{x \to 3} \left (\dfrac{x^2−9}{x−3} \right )\)
- Answer
-
\(6\)
8) \(\lim \limits_{x \to −1} \left (\dfrac{x^2−2x−3}{x+1} \right )\)
9) \(\lim \limits_{x \to \frac{3}{2}} \left (\dfrac{6x^2−17x+12}{2x−3} \right )\)
- Answer
-
\(\dfrac{1}{2}\)
10) \(\lim \limits_{ x \to −\frac{7}{2}} \left (\dfrac{8x^2+18x−35}{2x+7} \right )\)
11) \(\lim \limits_{ x \to 3} \left (\dfrac{x^2−9}{x−5x+6} \right )\)
- Answer
-
\(6\)
12) \(\lim \limits_{ x \to −3} \left (\dfrac{−7x^4−21x^3}{−12x^4+108x^2} \right )\)
13) \(\lim \limits_{ x \to 3} \left (\dfrac{x^2+2x−3}{x−3} \right )\)
- Answer
-
does not exist
14) \(\lim \limits_{ h \to 0} \left (\dfrac{(3+h)^3−27}{h} \right )\)
15) \(\lim \limits_{ h \to 0} \left (\dfrac{(2−h)^3−8}{h} \right )\)
- Answer
-
\(−12\)
16) \(\lim \limits_{ h \to 0} \left (\dfrac{(h+3)^2−9}{h} \right )\)
17) \(\lim \limits_{ h \to 0} \left (\dfrac{\sqrt{5−h}−\sqrt{5}}{h} \right )\)
- Answer
-
\(−\dfrac{\sqrt{5}}{10}\)
18) \(\lim \limits_{ x \to 0} \left (\dfrac{\sqrt{3−x}−\sqrt{3}}{x} \right )\)
19) \(\lim \limits_{ x \to 9} \left (\dfrac{x^2−81}{3−x} \right )\)
- Answer
-
\(−108\)
20) \(\lim \limits_{ x \to 1} \left (\dfrac{\sqrt{x}−x^2}{1−\sqrt{x}} \right )\)
21) \(\lim \limits_{ x \to 0}\left ( \dfrac{x}{\sqrt{1+2x}-1} \right )\)
- Answer
-
\(1\)
22) \(\lim \limits_{ x \to \frac{1}{2}} \left (\dfrac{x^2−\tfrac{1}{4}}{2x−1} \right )\)
23) \(\lim \limits_{ x \to 4} \left (\dfrac{x^3−64}{x^2−16} \right )\)
- Answer
-
\(6\)
24) \(\lim \limits_{ x \to 2^−} \left (\dfrac{|x−2|}{x−2} \right )\)
25) \(\lim \limits_{ x \to 2^+} \left (\dfrac{| x−2 |}{x−2} \right )\)
- Answer
-
\(1\)
26) \(\lim \limits_{ x \to 2} \left (\dfrac{| x−2 |}{x−2} \right )\)
27) \(\lim \limits_{ x \to 4^−} \left (\dfrac{| x−4 |}{4−x} \right )\)
- Answer
-
\(1\)
28) \(\lim \limits_{ x \to 4^+} \left (\dfrac{| x−4 |}{4−x} \right )\)
29) \(\lim \limits_{ x \to 4} \left (\dfrac{| x−4 |}{4−x} \right )\)
- Answer
-
does not exist
30) \(\lim \limits_{ x \to 2} \left (\dfrac{−8+6x−x^2}{x−2} \right )\)
For the exercises 31-33, use the given information to evaluate the limits: \(\lim \limits_{x \to c}f(x)=3, \lim \limits_{x \to c} g(x)=5\)
31) \(\lim \limits_{x \to c} [ 2f(x)+\sqrt{g(x)} ]\)
- Answer
-
\(6+\sqrt{5}\)
32) \(\lim \limits_{x \to c} [ 3f(x)+\sqrt{g(x)} ]\)
33) \(\lim \limits_{x \to c}\dfrac{f(x)}{g(x)}\)
- Answer
-
\(\dfrac{3}{5}\)
For the exercises 34-43, evaluate the following limits.
34) \(\lim \limits_{x \to 2} \cos (πx)\)
35) \(\lim \limits_{x \to 2} \sin (πx)\)
- Answer
-
\(0\)
36) \(\lim \limits_{x \to 2} \sin \left (\dfrac{π}{x} \right )\)
37) \(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^+}f(x)\)
- Answer
-
\(−3\)
38) \(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0^−} f(x)\)
39) \(f(x)= \begin{cases} 2x^2+2x+1, && x≤0 \\ x−3, && x>0 ; \end{cases} \lim \limits_{x \to 0}f(x)\)
- Answer
-
does not exist; right-hand limit is not the same as the left-hand limit.
40) \(\lim \limits_{x \to 4} \dfrac{\sqrt{x+5}−3}{x−4}\)
41) \(\lim \limits_{x \to 2^+} (2x−〚x〛)\)
- Answer
-
\(2\)
42) \(\lim \limits_{x \to 2} \dfrac{\sqrt{x+7}−3}{x^2−x−2}\)
43) \(\lim \limits_{x \to 3^+}\dfrac{x^2}{x^2−9}\)
- Answer
-
Limit does not exist; limit approaches infinity.
For the exercises 44-53, find the average rate of change\(\dfrac{f(x+h)−f(x)}{h}\).
44) \(f(x)=x+1\)
45) \(f(x)=2x^2−1\)
- Answer
-
\(4x+2h\)
46) \(f(x)=x^2+3x+4\)
47) \(f(x)=x^2+4x−100\)
- Answer
-
\(2x+h+4\)
48) \(f(x)=3x^2+1\)
49) \(f(x)= \cos (x)\)
- Answer
-
\(\dfrac{\cos (x+h)− \cos (x)}{h}\)
50) \(f(x)=2x^3−4x\)
51) \(f(x)=\dfrac{1}{x}\)
- Answer
-
\(\dfrac{−1}{x(x+h)}\)
52) \(f(x)=\dfrac{1}{x^2}\)
53) \(f(x)=\sqrt{x}\)
- Answer
-
\(\dfrac{−1}{\sqrt{x+h}+\sqrt{x}}\)
Graphical
54) Find an equation that could be represented by the Figure below.
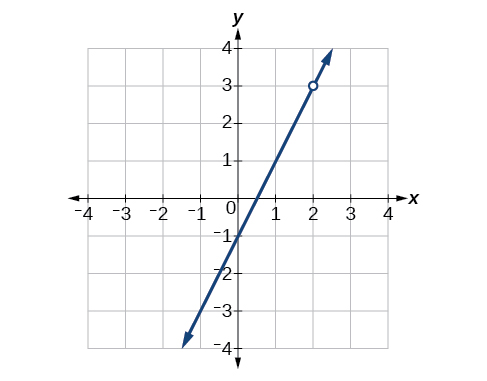
- Answer
-
\(f(x)=\dfrac{x^2+5x+6}{x+3}\)
For the exercises 56-57, refer to the Figure below.
56) What is the right-hand limit of the function as \(x\) approaches \(0\)?
57) What is the left-hand limit of the function as \(x\) approaches \(0\)?
- Answer
-
does not exist
Real-World Applications
58) The position function \(s(t)=−16t^2+144t\) gives the position of a projectile as a function of time. Find the average velocity (average rate of change) on the interval \([ 1,2 ]\).
59) The height of a projectile is given by \(s(t)=−64t^2+192t\) Find the average rate of change of the height from \(t=1\) second to \(t=1.5\) seconds.
- Answer
-
\(52\)
60) The amount of money in an account after \(t\) years compounded continuously at \(4.25\%\) interest is given by the formula \(A=A_0e^{0.0425t}\),where \(A_0\) is the initial amount invested. Find the average rate of change of the balance of the account from \(t=1\) year to \(t=2\) years if the initial amount invested is \(\$1,000.00.\)
12.3: Continuity
A function that remains level for an interval and then jumps instantaneously to a higher value is called a stepwise function. This function is an example. A function that has any hole or break in its graph is known as a discontinuous function. A stepwise function, such as parking-garage charges as a function of hours parked, is an example of a discontinuous function. We can check three different conditions to decide if a function is continuous at a particular number.
Verbal
1) State in your own words what it means for a function \(f\) to be continuous at \(x=c\).
- Answer
-
Informally, if a function is continuous at \(x=c\), then there is no break in the graph of the function at \(f(c)\), and \(f(c)\) is defined.
2) State in your own words what it means for a function to be continuous on the interval \((a,b)\).
Algebraic
For the exercises 3-22, determine why the function \(f\) is discontinuous at a given point \(a\) on the graph. State which condition fails.
3) \(f(x)=\ln | x+3 |,a=−3\)
- Answer
-
discontinuous at \(a=−3\); \(f(−3)\) does not exist
4) \(f(x)= \ln | 5x−2 |,a=\dfrac{2}{5}\)
5) \(f(x)=\dfrac{x^2−16}{x+4},a=−4\)
- Answer
-
removable discontinuity at \(a=−4; f(−4)\) is not defined
6) \(f(x)=\dfrac{x^2−16x}{x},a=0\)
7) \(f(x)= \begin{cases} x, && x≠3 \\ 2x, && x=3 \end{cases} a=3\)
- Answer
-
Discontinuous at \(a=3; \lim \limits_{x \to 3} f(x)=3,\) but \(f(3)=6,\) which is not equal to the limit.
8) \(f(x) = \begin{cases} 5, &&x≠0 \\ 3, && x=0 \end{cases} a=0\)
9) \(f(x)= \begin{cases} \dfrac{1}{2−x}, && x≠2 \\ 3, &&x=2 \end{cases} a=2\)
- Answer
-
\(\lim \limits_{x \to 2}f(x)\) does not exist.
10) \(f(x)= \begin{cases} \dfrac{1}{x+6}, && x=−6 \\ x^2, && x≠−6 \end{cases} a=−6\)
11) \(f(x)=\begin{cases} 3+x, &&x<1 \\ x, &&x=1 \\ x^2, && x>1 \end{cases} a=1\)
- Answer
-
\(\lim \limits_{x \to 1^−}f(x)=4;\lim \limits_{x \to 1^+}f(x)=1.\) Therefore, \(\lim \limits_{x \to 1}f(x)\) does not exist.
12) \(f(x)= \begin{cases} 3−x, && x<1 \\ x, && x=1 \\ 2x^2, && x>1 \end{cases} a=1\)
13) \(f(x)= \begin{cases} 3+2x, && x<1 \\ x, && x=1 \\ −x^2, && x>1 \end{cases} a=1\)
- Answer
-
\(\lim \limits_{x \to 1^−} f(x)=5≠ \lim \limits_{x \to 1^+}f(x)=−1\). Thus \(\lim \limits_{x \to 1}f(x)\) does not exist.
14) \(f(x)= \begin{cases} x^2, &&x<−2 \\ 2x+1, && x=−2 \\ x^3, && x>−2 \end{cases} a=−2\)
15) \(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3 \\ \dfrac{1}{x}, && x>−3 \end{cases} a=−3\)
- Answer
-
\(\lim \limits_{x to −3^+}f(x)=−\dfrac{1}{3}\)
Therefore, \(\lim \limits_{x \to −3} f(x)\) does not exist.
16) \(f(x)= \begin{cases} \dfrac{x^2−9}{x+3}, && x<−3 \\ x−9, && x=−3\\ −6, && x>−3 \end{cases} a=3\)
17) \(f(x)=\dfrac{x^2−4}{x−2}, a=2\)
- Answer
-
\(f(2)\) is not defined.
18) \(f(x)=\dfrac{25−x^2}{x^2−10x+25}, a=5\)
19) \(f(x)=\dfrac{x^3−9x}{x^2+11x+24}, a=−3\)
- Answer
-
\(f(−3)\) is not defined.
20) \(f(x)=\dfrac{x^3−27}{x^2−3x}, a=3\)
21) \(f(x)=\dfrac{x}{|x|}, a=0\)
- Answer
-
\(f(0)\) is not defined.
22) \(f(x)=\dfrac{2|x+2|}{x+2}, a=−2\)
For the exercises 23-35, determine whether or not the given function \(f\) is continuous everywhere. If it is continuous everywhere it is defined, state for what range it is continuous. If it is discontinuous, state where it is discontinuous.
23) \(f(x)=x^3−2x−15\)
- Answer
-
Continuous on \((−∞,∞)\)
24) \(f(x)=\dfrac{x^2−2x−15}{x−5}\)
25) \(f(x)=2⋅3^{x+4}\)
- Answer
-
Continuous on \((−∞,∞)\)
26) \(f(x)=− \sin (3x)\)
27) \(f(x)=\dfrac{|x−2|}{x^2−2x}\)
- Answer
-
Discontinuous at \(x=0\) and\(x=2\)
28) \(f(x)= \tan (x)+2\)
29) \(f(x)=2x+\dfrac{5}{x}\)
- Answer
-
Discontinuous at \(x=0\)
30) \(f(x)=\log _2 (x)\)
31) \(f(x)= \ln x^2 \)
- Answer
-
Continuous on \((0,∞)\)
32) \(f(x)=e^{2x}\)
33) \(f(x)=\sqrt{x−4}\)
- Answer
-
Continuous on \([4,∞)\)
34) \(f(x)= \sec (x)−3\)
35) \(f(x)=x^2+ \sin (x)\)
- Answer
-
Continuous on \((−∞,∞)\).
36) Determine the values of \(b\) and \(c\) such that the following function is continuous on the entire real number line.
\[f(x)= \begin{cases}x+1, && 1<x<3 \\ x^2+bx+c, &&|x−2|≥1 \end{cases} \nonumber \]
Graphical
For the exercises 37-39, refer to the Figure below. Each square represents one square unit. For each value of \(a\), determine which of the three conditions of continuity are satisfied at \(x=a\) and which are not.
37) \(x=−3\)
- Answer
-
\(1\), but not \(2\) or \(3\)
38) \(x=2\)
39) \(x=4\)
- Answer
-
\(1\) and \(2\), but not \(3\)
For the exercises 40-43, use a graphing utility to graph the function \(f(x)= \sin \left (\dfrac{12π}{x} \right )\) as in Figure. Set the \(x\)-axis a short distance before and after \(0\) to illustrate the point of discontinuity.
40) Which conditions for continuity fail at the point of discontinuity?
41) Evaluate \(f(0)\).
- Answer
-
\(f(0)\) is undefined.
42) Solve for \(x\) if \(f(x)=0\).
43) What is the domain of \(f(x)\)?
- Answer
-
\((−∞,0)∪(0,∞)\)
For the exercises 44-45, consider the function shown in the Figure below.
44) At what \(x\)-coordinates is the function discontinuous?
45) What condition of continuity is violated at these points?
- Answer
-
At \(x=−1\), the limit does not exist. At \(x=1, f(1)\) does not exist.
At \(x=2\), there appears to be a vertical asymptote, and the limit does not exist.
46) Consider the function shown in the Figure below. At what \(x\)-coordinates is the function discontinuous? What condition(s) of continuity were violated?
47) Construct a function that passes through the origin with a constant slope of \(1\), with removable discontinuities at \(x=−7\) and \(x=1\).
- Answer
-
\(\dfrac{x^3+6x^2−7x}{(x+7)(x−1)}\)
48) The function \(f(x)=\dfrac{x^3−1}{x−1}\) is graphed in the Figure below. It appears to be continuous on the interval \([−3,3]\), but there is an \(x\)-value on that interval at which the function is discontinuous. Determine the value of \(x\) at which the function is discontinuous, and explain the pitfall of utilizing technology when considering continuity of a function by examining its graph.
49) Find the limit \(\lim \limits_{ x \to 1}f(x)\) and determine if the following function is continuous at \(x=1\):
\[fx= \begin{cases} x^2+4 && x≠1 \\ 2 && x=1\end{cases} \nonumber \]
- Answer
-
The function is discontinuous at \(x=1\) because the limit as \(x\) approaches \(1\) is \(5\) and \(f(1)=2\).
50) The graph of \(f(x)= \dfrac{\sin (2x)}{x}\) is shown in the Figure below. Is the function \(f(x)\) continuous at \(x=0?\) Why or why not?
12.4: Derivatives
Change divided by time is one example of a rate. The rates of change in the previous examples are each different. In other words, some changed faster than others. If we were to graph the functions, we could compare the rates by determining the slopes of the graphs.
Verbal
1) How is the slope of a linear function similar to the derivative?
- Answer
-
The slope of a linear function stays the same. The derivative of a general function varies according to \(x\). Both the slope of a line and the derivative at a point measure the rate of change of the function.
2) What is the difference between the average rate of change of a function on the interval \([x,x+h]\) and the derivative of the function at \(x\)?
3) A car traveled \(110\) miles during the time period from 2:00 P.M. to 4:00 P.M. What was the car's average velocity? At exactly 2:30 P.M., the speed of the car registered exactly \(62\) miles per hour. What is another name for the speed of the car at 2:30 P.M.? Why does this speed differ from the average velocity?
- Answer
-
Average velocity is \(55\) miles per hour. The instantaneous velocity at 2:30 p.m. is \(62\) miles per hour. The instantaneous velocity measures the velocity of the car at an instant of time whereas the average velocity gives the velocity of the car over an interval.
4) Explain the concept of the slope of a curve at point \(x\).
5) Suppose water is flowing into a tank at an average rate of \(45\) gallons per minute. Translate this statement into the language of mathematics.
- Answer
-
The average rate of change of the amount of water in the tank is \(45\) gallons per minute. If \(f(x)\) is the function giving the amount of water in the tank at any time \(t\), then the average rate of change of \(f(x)\) between \(t=a\) and \(t=b\) is \(f(a)+45(b−a)\).
Algebraic
For the exercises 6-17, use the definition of derivative \(\lim \limits_{ h \to 0}\dfrac{f(x+h)-f(x)}{h}\) to calculate the derivative of each function.
6) \(f(x)=3x-4\)
7) \(f(x)=-2x+1\)
- Answer
-
\(f'(x)=-2\)
8) \(f(x)=x^2-2x+1\)
9) \(f(x)=2x^2+x-3\)
- Answer
-
\(f'(x)=4x+1\)
10) \(f(x)=2x^2+5\)
11) \(f(x)=\dfrac{-1}{x-2}\)
- Answer
-
\(f'(x)=\dfrac{1}{(x-2)^2}\)
12) \(f(x)=\dfrac{2+x}{1-x}\)
13) \(f(x)=\dfrac{5-2x}{3+2x}\)
- Answer
-
\(\dfrac{-16}{(3+2x)^2}\)
14) \(f(x)=\sqrt{1+3x}\)
15) \(f(x)=3x^3-x^2+2x+5\)
- Answer
-
\(f'(x)=9x^2-2x+2\)
16) \(f(x)=5\)
17) \(f(x)=5\pi\)
- Answer
-
\(f'(x)=0\)
For the exercises 18-21, find the average rate of change between the two points.
18) \((-2,0)\) and \((-4,5)\)
19) \((4,-3)\) and \((-2,-1)\)
- Answer
-
\(-\dfrac{1}{3}\)
20) \((0,5)\) and \((6,5)\)
21) \((7,-2)\) and \((7,10)\)
- Answer
-
undefined
For the polynomial functions 22-25, find the derivatives.
22) \(f(x)=x^3+1\)
23) \(f(x)=-3x^2-7x=6\)
- Answer
-
\(f'(x)=-6x-7\)
24) \(f(x)=7x^2\)
25) \(f(x)=3x^3+2x^2+x-26\)
- Answer
-
\(f'(x)=9x^2+4x+1\)
For the functions 26-28, find the equation of the tangent line to the curve at the given point \(x\) on the curve.
26) \(f(x)=2x^2-3x\; \; x=3\)
27) \(f(x)=x^2+1\; \; x=2\)
- Answer
-
\(y=12x-15\)
28) \(f(x)=\sqrt{x}\; \; x=9\)
29) For the following exercise, find \(k\) such that the given line is tangent to the graph of the function.
\[f(x)=x^2-kx\; \; y=4x-9 \nonumber \]
- Answer
-
\(k=-10\) or \(k=2\)
Graphical
For the exercises 30-33, consider the graph of the function \(f\) and determine where the function is continuous/discontinuous and differentiable/not differentiable.
30)
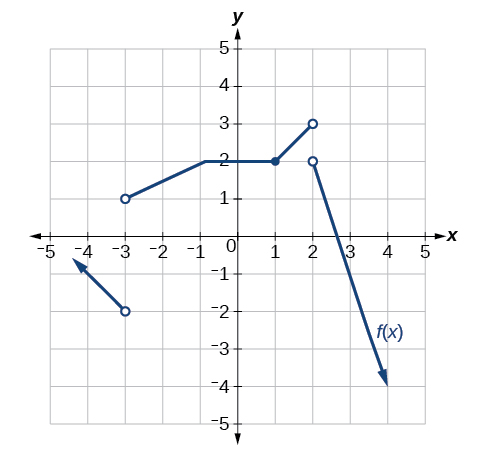
31)
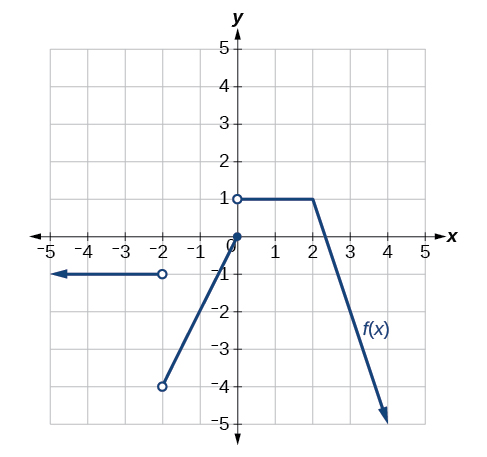
- Answer
-
Discontinuous at \(x=-2\) and \(x=0\). Not differentiable at \(-2, 0, 2\).
32)
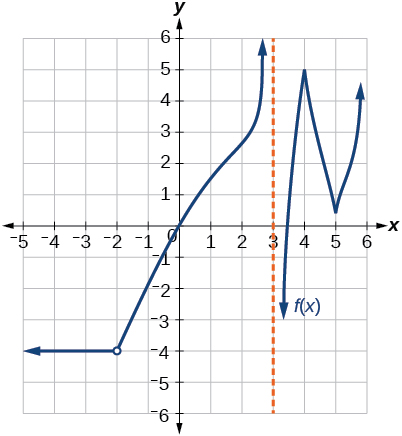
33)
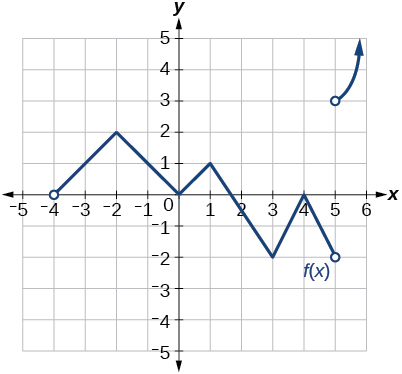
- Answer
-
Discontinuous at \(x=5\). Not differentiable at \(-4, -2, 0, 1, 3, 4, 5\).
For the exercises 34-43, use the Figure below to estimate either the function at a given value of \(x\) or the derivative at a given value of \(x\), as indicated.
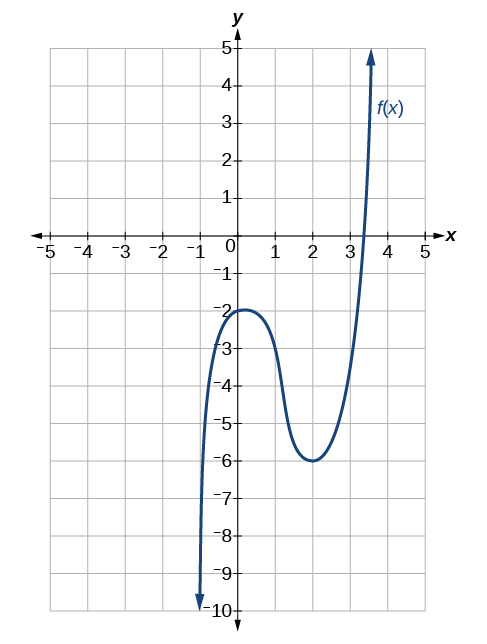
34) \(f(-1)\)
35) \(f(0)\)
- Answer
-
\(f(0)=-2\)
36) \(f(1)\)
37) \(f(2)\)
- Answer
-
\(f(2)=-6\)
38) \(f(3)\)
39) \(f'(-1)\)
- Answer
-
\(f'(-1)=9\)
40) \(f'(0)\)
41) \(f'(1)\)
- Answer
-
\(f'(1)=-3\)
42) \(f'(2)\)
43) \(f'(3)\)
- Answer
-
\(f'(3)=9\)
44) Sketch the function based on the information below:
\[f'(x)=2x, f(2)=4 \nonumber \]
Technology
45) Numerically evaluate the derivative. Explore the behavior of the graph of \(f(x)=x^2\) around \(x=1\) by graphing the function on the following domains: \([0.9,1.1], [0.99,1.01], [0.999,1.001], [0.9999, 1.0001]\). We can use the feature on our calculator that automatically sets Ymin and Ymax to the Xmin and Xmax values we preset. (On some of the commonly used graphing calculators, this feature may be called ZOOM FIT or ZOOM AUTO). By examining the corresponding range values for this viewing window, approximate how the curve changes at \(x=1\), that is, approximate the derivative at \(x=1\).
- Answer
-
Answers vary. The slope of the tangent line near \(x=1\) is \(2\).
Real-World Applications
For the exercises 46-50, explain the notation in words. The volume \(f(t)\) of a tank of gasoline, in gallons, \(t\) minutes after noon.
46) \(f(0)=600\)
47) \(f'(30)=-20\)
- Answer
-
At 12:30 p.m., the rate of change of the number of gallons in the tank is \(-20\) gallons per minute. That is, the tank is losing \(20\) gallons per minute.
48) \(f(30)=0\)
49) \(f'(200)=30\)
- Answer
-
At \(200\) minutes after noon, the volume of gallons in the tank is changing at the rate of \(30\) gallons per minute.
50) \(f(240)=500\)
For the exercises 51-55, explain the functions in words. The height, \(s\), of a projectile after \(t\) seconds is given by \(s(t)=-16t^2+80t\).
51) \(s(2)=96\)
- Answer
-
The height of the projectile after \(2\) seconds is \(96\) feet.
52) \(s'(2)=16\)
53) \(s(3)=96\)
- Answer
-
The height of the projectile at \(t=3\) seconds is \(96\) feet.
54) \(s'(3)=-16\)
55) \(s(0)=0, s(5)=0\)
- Answer
-
The height of the projectile is zero at \(t=0\) and again at \(t=5\). In other words, the projectile starts on the ground and falls to earth again after \(5\) seconds.
For the exercises 56-57, the volume \(V\) of a sphere with respect to its radius \(r\) is given by \(V=\dfrac{4}{3}\pi r^3\).
56) Find the average rate of change of \(V\) as \(r\) changes from \(1\) cm to \(2\) cm.
57) Find the instantaneous rate of change of \(V\) when \(r=3\) cm.
- Answer
-
\(36\pi \)
For the exercises 58-60, the revenue generated by selling \(x\) items is given by \(R(x)=2x^2+10x\).
58) Find the average change of the revenue function as \(x\) changes from \(x=10\) to \(x=20\).
59) Find \(R'(10)\) and interpret.
- Answer
-
\(\$50.00\) per unit, which is the instantaneous rate of change of revenue when exactly \(10\) units are sold.
60) Find \(R'(15)\) and interpret. Compare \(R'(15)\) to \(R'(10)\), and explain the difference.
For the exercises 61-63, the cost of producing \(x\) cellphones is described by the function \(C(x)=x^2-4x+1000\).
61) Find the average rate of change in the total cost as \(x\) changes from \(x=10\) to \(x=15\).
- Answer
-
\(\$21\) per unit
62) Find the approximate marginal cost, when \(15\) cellphones have been produced, of producing the \(16^{th}\) cellphone.
63) Find the approximate marginal cost, when \(20\) cellphones have been produced, of producing the \(21^{st}\) cellphone.
- Answer
-
\(\$36\)
Extension
For the exercises 64-67, use the definition for the derivative at a point \(x=a\), \(\lim \limits_{x \to a}\dfrac{f(x)-f(a)}{x-a}\), to find the derivative of the functions.
64) \(f(x)=\dfrac{1}{x^2}\)
65) \(f(x)=5x^2-x+4\)
- Answer
-
\(f'(x)=10a-1\)
66) \(f(x)=-x^2+4x+7\)
67) \(f(x)=\dfrac{-4}{3-x^2}\)
- Answer
-
\(\dfrac{4}{(3-x)^2}\)
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


