2.1: The Law of Sines
- Page ID
- 3254
If a triangle has sides of lengths \(a \), \(b \), and \(c \) opposite the angles \(A \), \(B \), and \(C \), respectively, then
\[\label{2.1} \dfrac{a}{\sin\;A} ~=~ \dfrac{b}{\sin\;B} ~=~ \dfrac{c}{\sin\;C} ~. \]
Note that by taking reciprocals, Equation \ref{2.1} can be written as
\[\label{2.2}
\dfrac{\sin\;A}{a} ~=~ \dfrac{\sin\;B}{b} ~=~ \dfrac{\sin\;C}{c} ~,
\nonumber \]
and it can also be written as a collection of three equations:
\[\label{2.3}
\dfrac{a}{b} ~=~ \dfrac{\sin\;A}{\sin\;B} ~~,\quad \dfrac{a}{c} ~=~ \dfrac{\sin\;A}{\sin\;C} ~~,\quad
\dfrac{b}{c} ~=~ \dfrac{\sin\;B}{\sin\;C}
\nonumber \]
Another way of stating the Law of Sines is: The sides of a triangle are proportional to the sines of their opposite angles.
To prove the Law of Sines, let \(\triangle\,ABC \) be an oblique triangle. Then \(\angle \,ABC \) can be acute, as in Figure \(\PageIndex{1}\)(a), or it can be obtuse, as in Figure \(\PageIndex{1}\)(b). In each case, draw the altitude from the vertex at \(C \) to the side \(\overline{AB} \). In Figure \(\PageIndex{1}\)(a) the altitude lies inside the triangle, while in Figure \(\PageIndex{1}\)(b) the altitude lies outside the triangle.
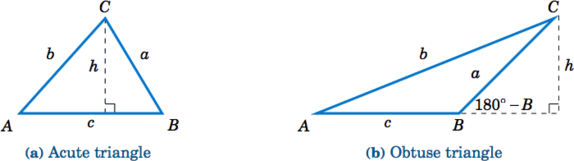
Let \(h \) be the height of the altitude. For each triangle in Figure \(\PageIndex{1}\), we see that
\[ \dfrac{h}{b} ~=~ \sin\;A\label{2.4} \]
and
\[ \dfrac{h}{a} ~=~ \sin\;B\label{2.5} \]
in Figure \(\PageIndex{1}\)(b), \(\dfrac{h}{a} = \sin\;(180^\circ - B) = \sin\;B \) as shown previously). Thus, solving for \(h \) in Equation \ref{2.5} and substituting that into Equation \ref{2.4} gives
\[\dfrac{a\;\sin\;B}{b} ~=~ \sin\;A ~,\label{2.6} \]
and so putting \(a \) and \(A \) on the left side and \(b \) and \(B \) on the right side, we get
\[\dfrac{a}{\sin\;A} ~=~ \dfrac{b}{\sin\;B} ~.\label{2.7} \]
By a similar argument, drawing the altitude from \(A \) to \(\overline{BC} \) gives
\[\label{2.8} \dfrac{b}{\sin\;B} ~=~ \dfrac{c}{\sin\;C} ~, \]
so putting the last two equations together proves the theorem.
\(\square\)
Note that we did not prove the Law of Sines for right triangles, since it turns out (see Exercise 12) to be trivially true for that case.
Solve the triangle \(\triangle\,ABC \) given \(a = 10 \), \(A =41^\circ \), and \(C = 75^\circ \).
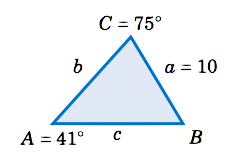
Solution
We can find the third angle by subtracting the other two angles from \(180^\circ \), then use the law of sines to find the two unknown sides. In this example we need to find \(B \), \(b \), and \(c \). First, we see that
\[B ~=~ 180^\circ ~-~ A ~-~ C ~=~ 180^\circ ~-~ 41^\circ ~-~ 75^\circ \quad\Rightarrow\quad
\boxed{B ~=~ 64^\circ} ~. \nonumber \]
So by the Law of Sines we have
\[\begin{align}
\dfrac{b}{\sin\;B} ~&=~ \dfrac{a}{\sin\;A} \quad&\Rightarrow\quad b ~&=~ \dfrac{a\;\sin\;B}{\sin\;A}
~&=~ \dfrac{10\;\sin\;64^\circ}{\sin\;41^\circ} \quad&\Rightarrow\quad \boxed{b ~=~ 13.7}
~,~\text{and}\\[4pt]\nonumber
\dfrac{c}{\sin\;C} ~&=~ \dfrac{a}{\sin\;A} \quad&\Rightarrow\quad c ~&=~ \dfrac{a\;\sin\;C}{\sin\;A}
~&=~ \dfrac{10\;\sin\;75^\circ}{\sin\;41^\circ} \quad&\Rightarrow\quad \boxed{c ~=~ 14.7} ~.
\end{align} \nonumber \]
Solve the triangle \(\triangle\,ABC \) given \(a = 18 \), \(A = 25^\circ \), and \(b = 30 \).
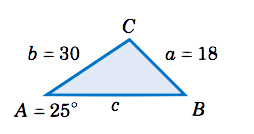
Solution
In this example we know the side \(a \) and its opposite angle \(A \), and we know the side \(b \). We can use the Law of Sines to find the other opposite angle \(B \), then find the third angle \(C \) by subtracting \(A \) and \(B \) from \(180^\circ \), then use the law of sines to find the third side \(c \). By the Law of Sines, we have
\[\dfrac{\sin\;B}{b} ~=~ \dfrac{\sin\;A}{a} \quad\Rightarrow\quad \sin\;B ~=~ \dfrac{b\;\sin\;A}{a} ~=~
\dfrac{30\;\sin\;25^\circ}{18} \quad\Rightarrow\quad \sin\;B ~=~ 0.7044 ~. \nonumber \]
Using the \(\fbox{\(\sin^{-1}\)}\) button on a calculator gives \(B = 44.8^\circ \). However, recall from Section 1.5 that \(\sin\;(180^\circ - B) = \sin\;B \). So there is a second possible solution for \(B \), namely \(180^\circ - 44.8^\circ = 135.2^\circ \). Thus, we have to solve twice for \(C \) and \(c \) : once for \(B = 44.8^\circ \) and once for \(B = 135.2^\circ\):
\[\begin{array}{c|c}
\boxed{B = 44.8^\circ} & \boxed{B = 135.2^\circ} \\
C = 180^\circ - A - B = 180^\circ - 25^\circ - 44.8^\circ = 110.2^\circ &
C = 180^\circ - A - B = 180^\circ - 25^\circ - 135.2^\circ = 19.8^\circ \\
\dfrac{c}{\sin\;C} = \dfrac{a}{\sin\;A} ~\Rightarrow~ c = \dfrac{a\;\sin\;C}{\sin\;A}
= \dfrac{18\;\sin\;110.2^\circ}{\sin\;25^\circ} &
\dfrac{c}{\sin\;C} = \dfrac{a}{\sin\;A} ~\Rightarrow~ c = \dfrac{a\;\sin\;C}{\sin\;A}
= \dfrac{18\;\sin\;19.8^\circ}{\sin\;25^\circ} \\
\Rightarrow~ c = 40 & \Rightarrow~ c = 14.4
\end{array} \nonumber \]
Hence, \(\fbox{\(B = 44.8^\circ \), \(C = 110.2^\circ \),\(c = 40\)}\) and \(\fbox{\(B = 135.2^\circ \), \(C = 19.8^\circ \), \(c = 14.4\)}\) are the two possible sets of solutions. This means that there are two possible triangles, as shown in Figure \(\PageIndex{2}\).
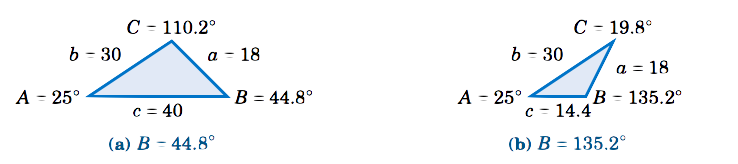
In Example \(\PageIndex{2}\) we saw what is known as the ambiguous case. That is, there may be more than one solution. It is also possible for there to be exactly one solution or no solution at all.
Solve the triangle \(\triangle\,ABC \) given \(a = 5 \), \(A = 30^\circ \), and \(b = 12 \).
Solution
By the Law of Sines, we have
\[\dfrac{\sin\;B}{b} ~=~ \dfrac{\sin\;A}{a} \quad\Rightarrow\quad \sin\;B ~=~ \dfrac{b\;\sin\;A}{a} ~=~
\dfrac{12\;\sin\;30^\circ}{5} \quad\Rightarrow\quad \sin\;B ~=~ 1.2 ~,\nonumber \]
which is impossible since \(| \sin\;B | \le 1 \) for any angle \(B \). Thus, there is \(\fbox{no solution}\).
There is a way to determine how many solutions a triangle has in Case 2. For a triangle \(\triangle\,ABC \), suppose that we know the sides \(a \) and \(b \) and the angle \(A \). Draw the angle \(A\) and the side \(b \), and imagine that the side \(a \) is attached at the vertex at \(C \) so that it can "swing'' freely, as indicated by the dashed arc in Figure \(\PageIndex{3}\) below.
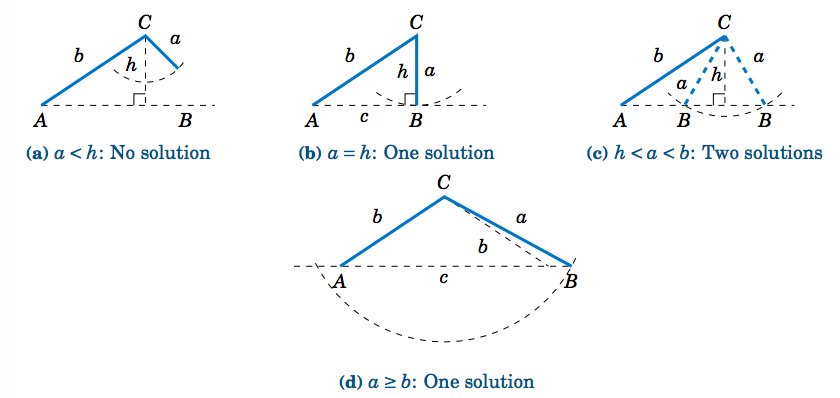
If \(A \) is acute, then the altitude from \(C \) to \(\overline{AB} \) has height \(h = b\;\sin\;A \). As we can see in Figure \(\PageIndex{3}\)(a)-(c), there is no solution when \(a < h \) (this was the case in Example 2.3); there is exactly one solution - namely, a right triangle - when \(a = h\); and there are two solutions when \(h < a < b \) (as was the case in Example 2.2). When \(a \ge b \) there is only one solution, even though it appears from Figure \(\PageIndex{3}\)(d) that there may be two solutions, since the dashed arc intersects the horizontal line at two points. However, the point of intersection to the left of \(A \) in Figure \(\PageIndex{3}\)(d) can not be used to determine \(B \), since that would make \(A \) an obtuse angle, and we assumed that \(A \) was acute.
If \(A \) is not acute (i.e. \(A \) is obtuse or a right angle), then the situation is simpler: there is no solution if \(a \le b \), and there is exactly one solution if \(a > b \) (see Figure \(\PageIndex{4}\)).
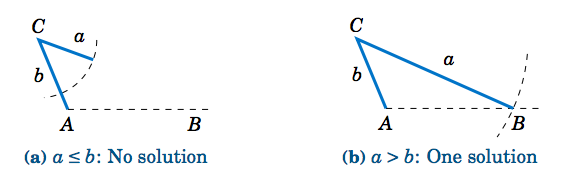
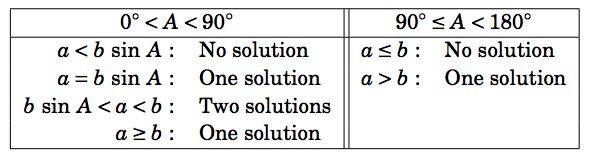
Table 2.1 summarizes the ambiguous case of solving \(\triangle\,ABC \) when given \(a \), \(A \), and \(b \). Of course, the letters can be interchanged, e.g. replace \(a \) and \(A \) by \(c\) and \(C \), etc.
Table 2.1 Summary of the ambiguous case
There is an interesting geometric consequence of the Law of Sines. Recall from Section 1.1 that in a right triangle the hypotenuse is the largest side. Since a right angle is the largest angle in a right triangle, this means that the largest side is opposite the largest angle. What the Law of Sines does is generalize this to any triangle:
In any triangle, the largest side is opposite the largest angle.
To prove this, let \(C \) be the largest angle in a triangle \(\triangle\,ABC \). If \(C = 90^\circ \) then we already know that its opposite side \(c \) is the largest side. So we just need to prove the result for when \(C \) is acute and for when \(C \) is obtuse. In both cases, we have \(A \le C \) and \(B \le C \). We will first show that \(\sin\;A \le \sin\;C \) and \(\sin\;B \le \sin\;C \).
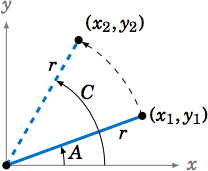
If \(C \) is acute, then \(A \) and \(B \) are also acute. Since \(A \le C \), imagine that \(A \) is in standard position in the \(xy\)-coordinate plane and that we rotate the terminal side of \(A \) counterclockwise to the terminal side of the larger angle \(C \), as in Figure \(\PageIndex{5}\). If we pick points \((x_{1},y_{1}) \) and \((x_{2},y_{2}) \) on the terminal sides of \(A \) and \(C \), respectively, so that their distance to the origin is the same number \(r \), then we see from the picture that \(y_{1} \le y_{2} \), and hence
\[ \sin\;A ~=~ \dfrac{y_{1}}{r} ~\le~ \dfrac{y_{2}}{r} ~=~ \sin\;C ~.
\nonumber \]
By a similar argument, \(B \le C \) implies that \(\sin\;B \le \sin\;C \). Thus, \(\sin\;A \le \sin\;C\) and \(\sin\;B \le \sin\;C \) when \(C \) is acute. We will now show that these inequalities hold when \(C \) is obtuse.
If \(C \) is obtuse, then \(180^\circ - C \) is acute, as are \(A \) and \(B \). If \(A > 180^\circ -C\) then \(A + C > 180^\circ \), which is impossible. Thus, we must have \(A \le 180^\circ - C \). Likewise, \(B \le 180^\circ - C \). So by what we showed above for acute angles, we know that \(\sin\;A \le \sin\;(180^\circ - C) \) and \(\sin\;B \le \sin\;(180^\circ - C) \). But we know from Section 1.5 that \(\sin\;C = \sin\;(180^\circ - C) \). Hence, \(\sin\;A \le \sin\;C\) and \(\sin\;B \le \sin\;C \) when \(C \) is obtuse.
Thus, \(\sin\;A \le \sin\;C \) if \(C \) is acute or obtuse, so by the Law of Sines we have
\[ \dfrac{a}{c} ~=~ \dfrac{\sin\;A}{\sin\;C} ~\le~ \dfrac{\sin\;C}{\sin\;C} ~=~ 1 \quad\Rightarrow\quad
\dfrac{a}{c} ~\le~ 1 \quad\Rightarrow\quad a ~\le~ c ~.
\nonumber \]
By a similar argument, \(b \le c \). Thus, \(a \le c \) and \(b \le c \), i.e. \(c \) is the largest side.
\(\square\)


