5.2: Properties of Graphs of Trigonometric Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
We saw in Section 5.1 how the graphs of the trigonometric functions repeat every 2π radians. In this section we will discuss this and other properties of graphs, especially for the sinusoidal functions (sine and cosine).
First, recall that the domain of a function f(x) is the set of all numbers x for which the function is defined. For example, the domain of f(x)=sinx is the set of all real numbers, whereas the domain of f(x)=tanx is the set of all real numbers except x=±π2, ±3π2, ±5π2, .... The range of a function f(x) is the set of all values that f(x) can take over its domain. For example, the range of f(x)=sinx is the set of all real numbers between −1 and 1 (i.e. the interval [−1,1]), whereas the range of f(x)=tanx is the set of all real numbers, as we can see from their graphs.
A function f(x) is periodic if there exists a number p>0 such that x+p is in the domain of f(x) whenever x is, and if the following relation holds:
f(x+p) = f(x)for all x
There could be many numbers p that satisfy the above requirements. If there is a smallest such number p, then we call that number the period of the function f(x).
The functions sinx, cosx, cscx, and secx all have the same period: 2π radians. We saw in Section 5.1 that the graphs of y=tanx and y=cotx repeat every 2π radians but they also repeat every π radians. Thus, the functions tanx and cotx have a period of π radians.
What is the period of f(x)=sin2x?
Solution
The graph of y=sin2x is shown in Figure 5.2.1, along with the graph of y=sinx for comparison, over the interval [0,2π]. Note that sin2x ``goes twice as fast'' as sinx.
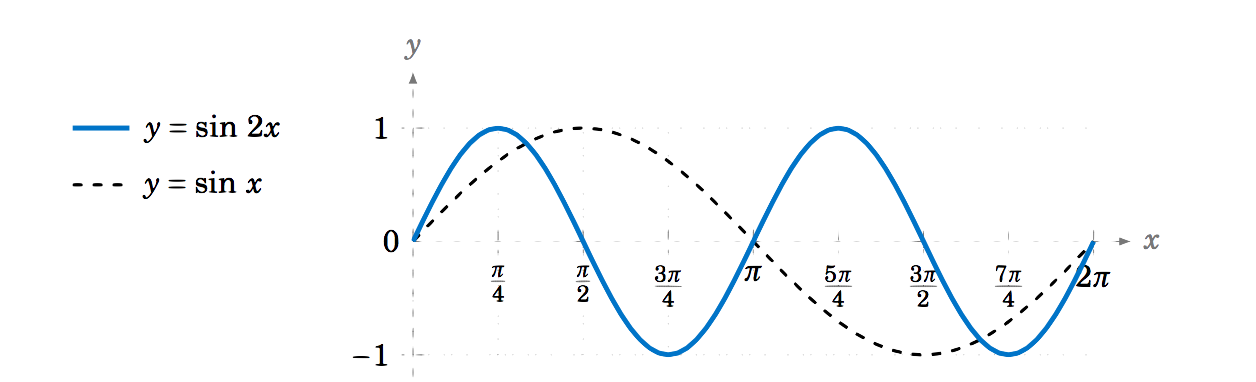
For example, for x from 0 to π2, sinx goes from 0 to 1, but sin2x is able to go from 0 to 1 quicker, just over the interval [0,π4]. While sinx takes a full 2π radians to go through an entire cycle (the largest part of the graph that does not repeat), sin2x goes through an entire cycle in just π radians. So the period of sin2x is π radians.
The above example made use of the graph of sin2x, but the period can be found analytically. Since sinx has period 2π, we know that sin(x+2π)=sinx for all x. Since 2x is a number for all x, this means in particular that sin(2x+2π)=sin2x for all x. Now define f(x)=sin2x. Then
f(x+π) = sin2(x+π)= sin(2x+2π)= sin2x(as we showed above)= f(x)
for all x, so the period p of sin2x is at most π, by our definition of period. We have to show that p>0 can not be smaller than π. To do this, we will use a proof by contradiction. That is, assume that 0<p<π, then show that this leads to some contradiction, and hence can not be true. So suppose 0<p<π. Then 0<2p<2π, and hence
sin2x = f(x)= f(x+p)(since p is the period of f(x))= sin2(x+p)= sin(2x+2p)
for all x. Since any number u can be written as 2x for some x (i.e u=2(u/2)), this means that sinu=sin(u+2p) for all real numbers u, and hence the period of sinx is as most 2p. This is a contradiction. Why? Because the period of sinx is 2π>2p. Hence, the period p of sin2x can not be less than π, so the period must equal π.
The above may seem like a lot of work to prove something that was visually obvious from the graph (and intuitively obvious by the "twice as fast'' idea). Luckily, we do not need to go through all that work for each function, since a similar argument works when sin2x is replaced by sinωx for any positive real number ω: instead of dividing 2π by 2 to get the period, divide by ω. And the argument works for the other trigonometric functions as well. Thus, we get:
For any number ω>0:
sinωx has period 2πωcscωx has period 2πωcosωx has period 2πωsecωx has period 2πωtanωx has period πωcotωx has period πω
If ω<0, then use sin(−A)=−sinA and cos(−A)=cosA (e.g. sin(−3x)=−sin3x).
The period of y=cos3x is 2π3 and the period of y=cos12x is 4π. The graphs of both functions are shown in Figure 5.2.2:

We know that −1≤sinx≤1 and −1≤cosx≤1 for all x. Thus, for a constant A≠0,
−|A| ≤ Asinx ≤ |A|and−|A| ≤ Acosx ≤ |A|
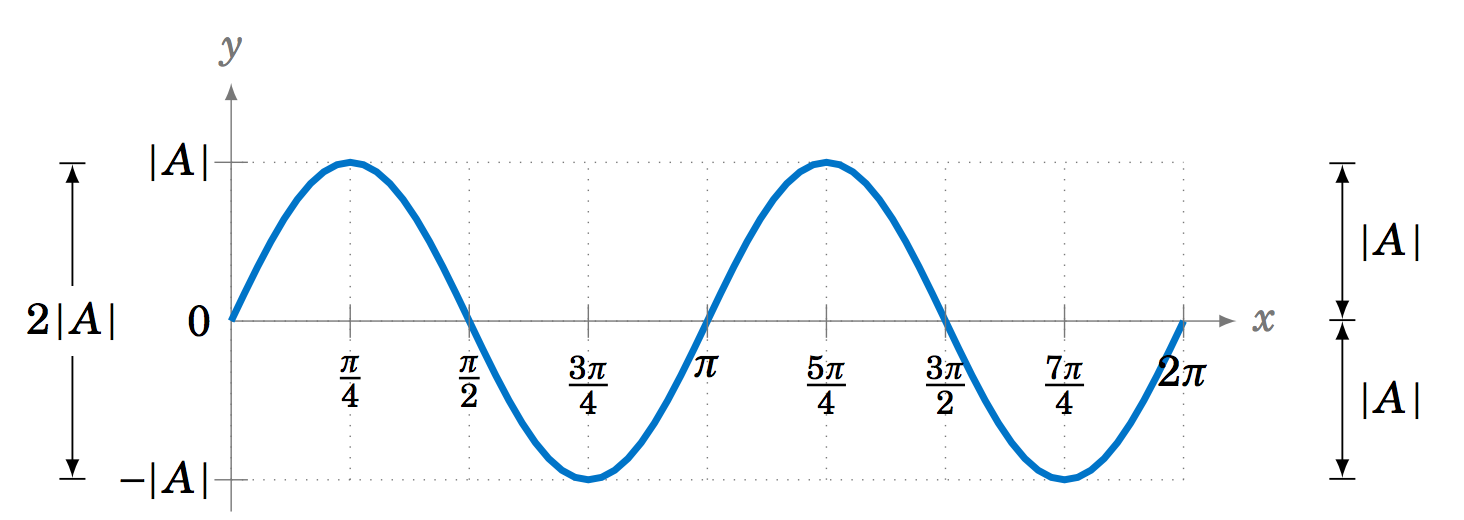
for all x. In this case, we call |A| the amplitude of the functions y=Asinx and y=Acosx. In general, the amplitude of a periodic curve f(x) is half the difference of the largest and smallest values that f(x) can take:
Amplitude of f(x) = (maximum of f(x)) − (minimum of f(x))2
In other words, the amplitude is the distance from either the top or bottom of the curve to the horizontal line that divides the curve in half, as in Figure 5.2.3.
Not all periodic curves have an amplitude. For example, tanx has neither a maximum nor a minimum, so its amplitude is undefined. Likewise, cotx, cscx, and secx do not have an amplitude. Since the amplitude involves vertical distances, it has no effect on the period of a function, and vice versa.
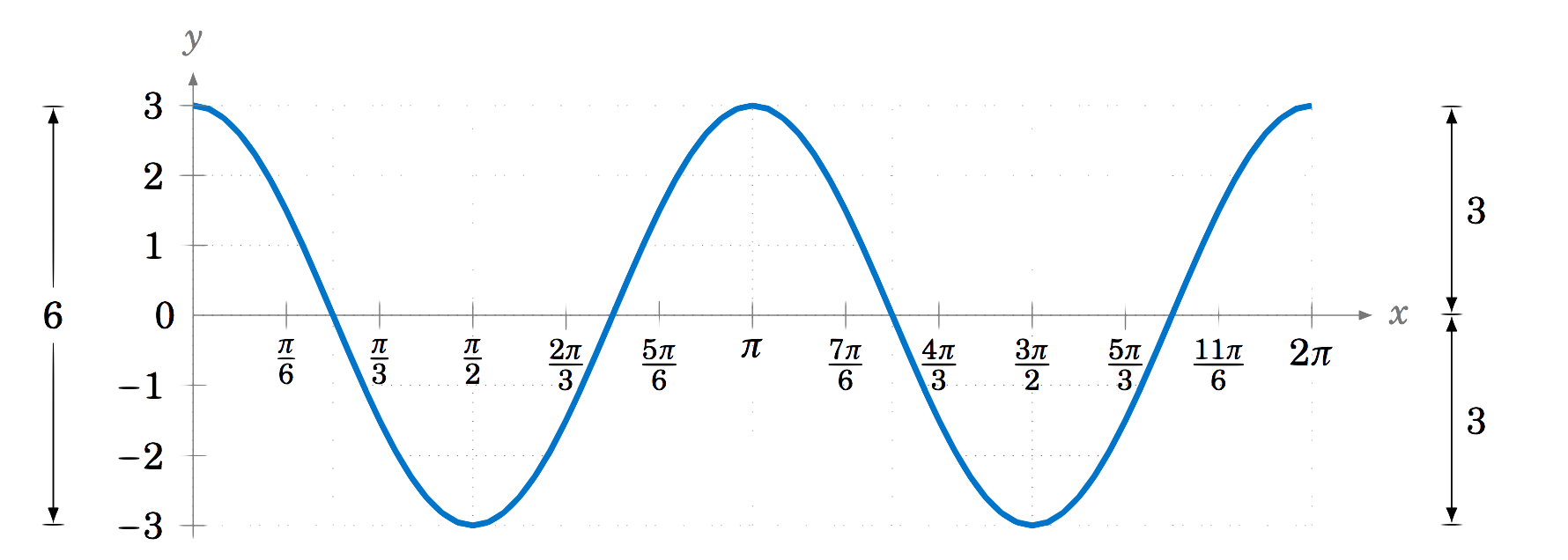
Find the amplitude and period of y=3cos2x.
Solution
The amplitude is |3|=3 and the period is 2π2=π. The graph is shown in Figure 5.2.4:
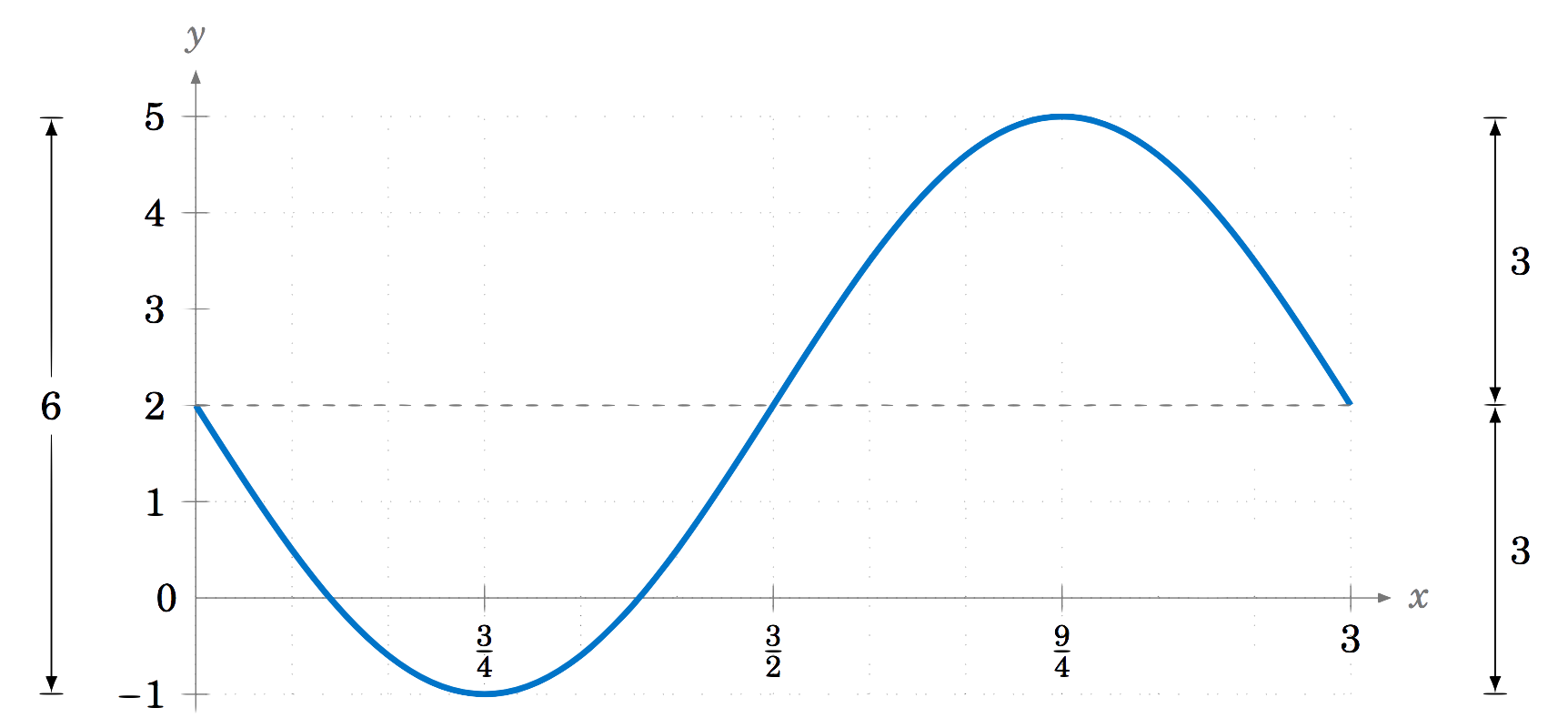
Find the amplitude and period of y=2−3sin2π3x.
Solution
The amplitude of −3sin2π3x is |−3|=3. Adding 2 to that function to get the function y=2−3sin2π3x does not change the amplitude, even though it does change the maximum and minimum. It just shifts the entire graph upward by 2. So in this case, we have
Amplitude = max − min2 = 5 − (−1)2 = 62 = 3 .
The period is 2π2π3=3. The graph is shown in Figure 5.2.5:
Find the amplitude and period of y=2sin(x2).
Solution
This is not a periodic function, since the angle that we are taking the sine of, x2, is not a linear function of x, i.e. is not of the form ax+b for some constants a and b. Recall how we argued that sin2x was ``twice as fast'' as sinx, so that its period was π instead of 2π. Can we say that sin(x2) is some constant times as fast as sinx? No. In fact, we see that the "speed'' of the curve keeps increasing as x gets larger, since x2 grows at a variable rate, not a constant rate. This can be seen in the graph of y=2sin(x2), shown in Figure 5.2.6:
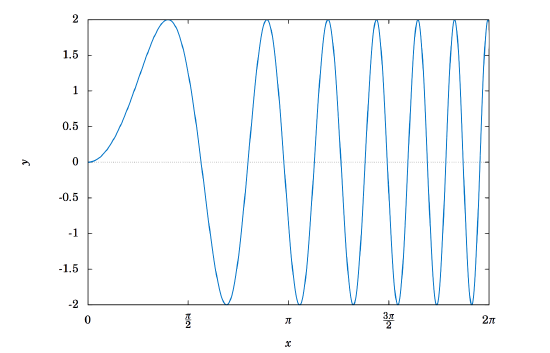
Notice how the curve "speeds up'' as x gets larger, making the "waves'' narrower and narrower. Thus, y=2sin(x2) has no period. Despite this, it appears that the function does have an amplitude, namely 2. To see why, note that since |sinθ|≤1 for all θ, we have
|2sin(x2)| = |2|⋅|sin(x2)| ≤ 2⋅1 = 2 .
In the exercises you will be asked to find values of x such that 2sin(x2) reaches the maximum value 2 and the minimum value −2. Thus, the amplitude is indeed 2.
Note: This curve is still sinusoidal despite not being periodic, since the general shape is still that of a "sine wave'', albeit one with variable cycles.
So far in our examples we have been able to determine the amplitudes of sinusoidal curves fairly easily. This will not always be the case.
Find the amplitude and period of y=3sinx+4cosx.
Solution
This is sometimes called a combination sinusoidal curve, since it is the sum of two such curves. The period is still simple to determine: since sinx and cosx each repeat every 2π radians, then so does the combination 3sinx+4cosx. Thus, y=3sinx+4cosx has period 2π. We can see this in the graph, shown in Figure 5.2.7:
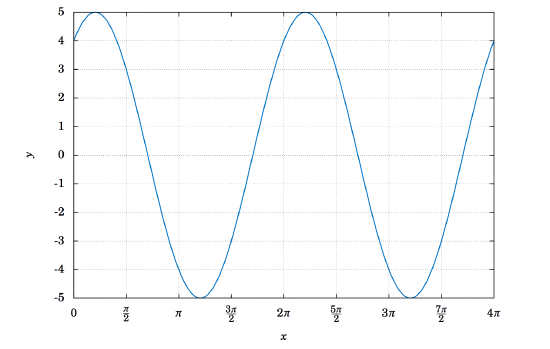
The graph suggests that the amplitude is 5, which may not be immediately obvious just by looking at how the function is defined. In fact, the definition y=3sinx+4cosx may tempt you to think that the amplitude is 7, since the largest that 3sinx could be is 3 and the largest that 4cosx could be is 4, so that the largest their sum could be is 3+4=7. However, 3sinx can never equal 3 for the same x that makes 4cosx equal to 4 (why?).
There is a useful technique (which we will discuss further in Chapter 6) for showing that the amplitude of y=3sinx+4cosx is 5. Let θ be the angle shown in the right
triangle in Figure 5.2.8. Then cosθ=35 and sinθ=45. We can use this as follows:
y = 3sinx + 4cosx= 5(35sinx + 45cosx)= 5(cosθsinx + sinθcosx)= 5sin(x+θ)(by the sine addition formula)
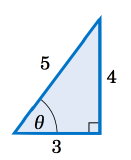
Thus, |y|=|5sin(x+θ)|=|5|⋅|sin(x+θ)|≤(5)(1)=5, so the amplitude of y=3sinx+4cosx is 5.
In general, a combination of sines and cosines will have a period equal to the lowest common multiple of the periods of the sines and cosines being added. In Example 5.9, sinx and cosx each have period 2π, so the lowest common multiple (which is always an integer multiple) is 1⋅2π=2π.
Find the period of y=cos6x+sin4x.
Solution
The period of cos6x is 2π6=π3, and the period of sin4x is 2π4=π2. The lowest common multiple of π3 and π2 is π:
1⋅π3 = π31⋅π2 = π22⋅π3 = 2π32⋅π2 = π3⋅π3 = π
Thus, the period of y=cos6x+sin4x is π. We can see this from its graph in Figure 5.2.9:
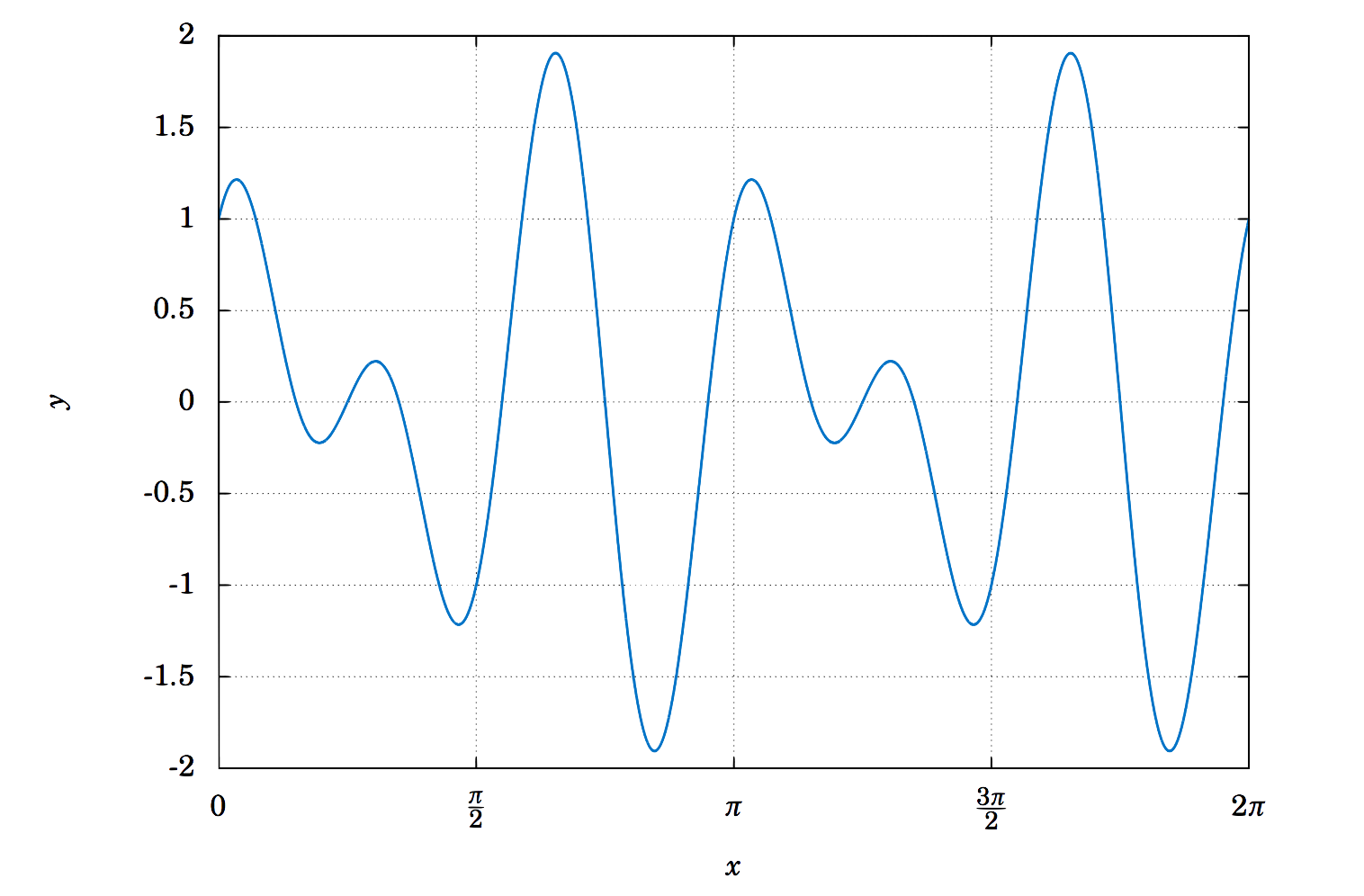
What about the amplitude? Unfortunately we can not use the technique from Example 5.9, since we are not taking the cosine and sine of the same angle; we are taking the cosine of 6x but the sine of 4x. In this case, it appears from the graph that the maximum is close to 2 and the minimum is close to −2. In Chapter 6, we will describe how to use a numerical computation program to show that the maximum and minimum are ±1.90596111871578, respectively (accurate to within ≈2.2204×10−16). Hence, the amplitude is 1.90596111871578.
Generalizing Example 5.9, an expression of the form asinωx+bcosωx is equivalent to √a2+b2sin(x+θ), where θ is an angle such that cosθ=a√a2+b2 and sinθ=b√a2+b2. So y=asinωx+bcosωx will have amplitude √a2+b2. Note that this method only works when the angle ωx is the same in both the sine and cosine terms.
We have seen how adding a constant to a function shifts the entire graph vertically. We will now see how to shift the entire graph of a periodic curve horizontally.
Consider a function of the form y=Asinωx, where A and ω are nonzero constants. For simplicity we will assume that A>0 and ω>0 (in general either one could be negative). Then the amplitude is A and the period is 2πω. The graph is shown in Figure 5.2.10.
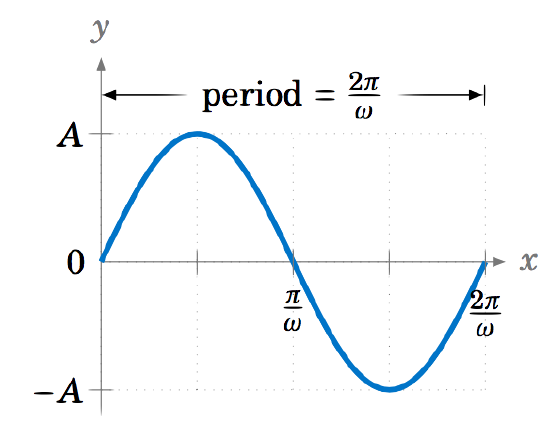
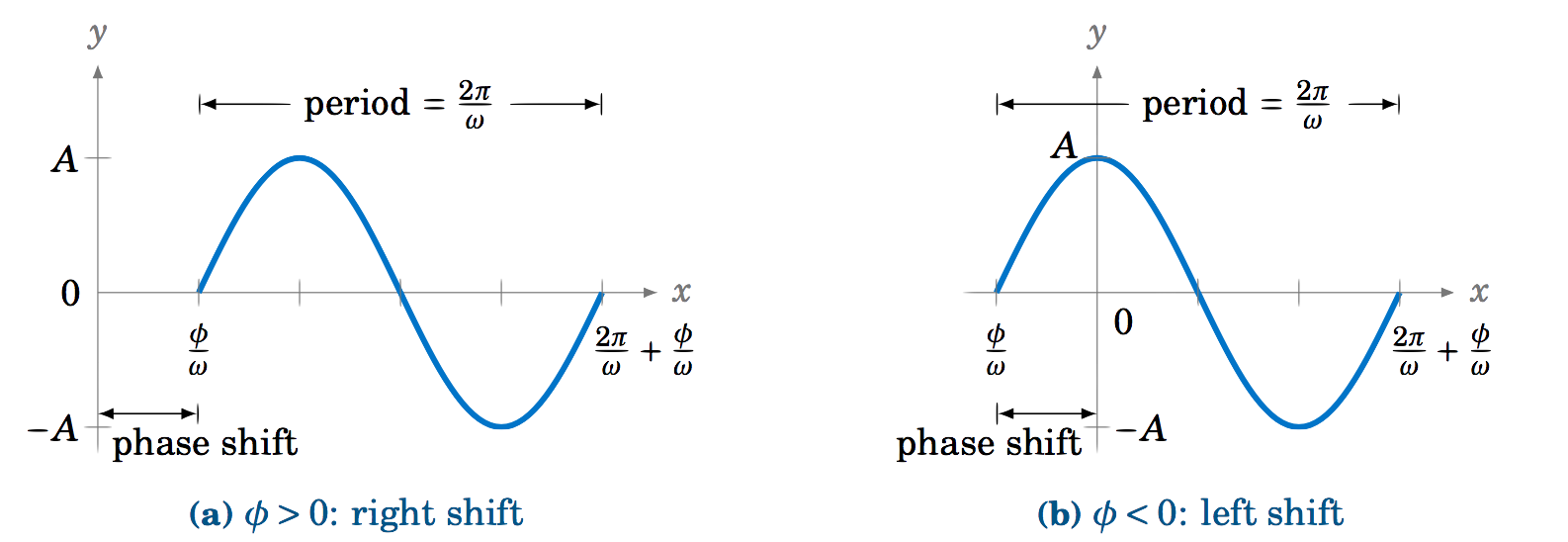
Now consider the function y=Asin(ωx−ϕ), where ϕ is some constant. The amplitude is still A, and the period is still 2πω, since ωx−ϕ is a linear function of x. Also, we know that the sine function goes through an entire cycle when its angle goes from 0 to 2π. Here, we are taking the sine of the angle ωx−ϕ. So as ωx−ϕ goes from 0 to 2π, an entire cycle of the function y=Asin(ωx−ϕ) will be traced out. That cycle starts when
ωx−ϕ = 0⇒x = ϕω
and ends when
ωx−ϕ = 2π⇒x = 2πω+ϕω .
Thus, the graph of y=Asin(ωx−ϕ) is just the graph of y=Asinωx shifted horizontally by ϕω, as in Figure 5.2.11. The graph is shifted to the right when ϕ>0, and to the left when ϕ<0. The amount ϕω of the shift is called the phase shift of the graph.
The phase shift is defined similarly for the other trigonometric functions.
Find the amplitude, period, and phase shift of y=3cos(2x−π).
Solution
The amplitude is 3, the period is 2π2=π, and the phase shift is π2. The graph is shown in Figure 5.2.12:
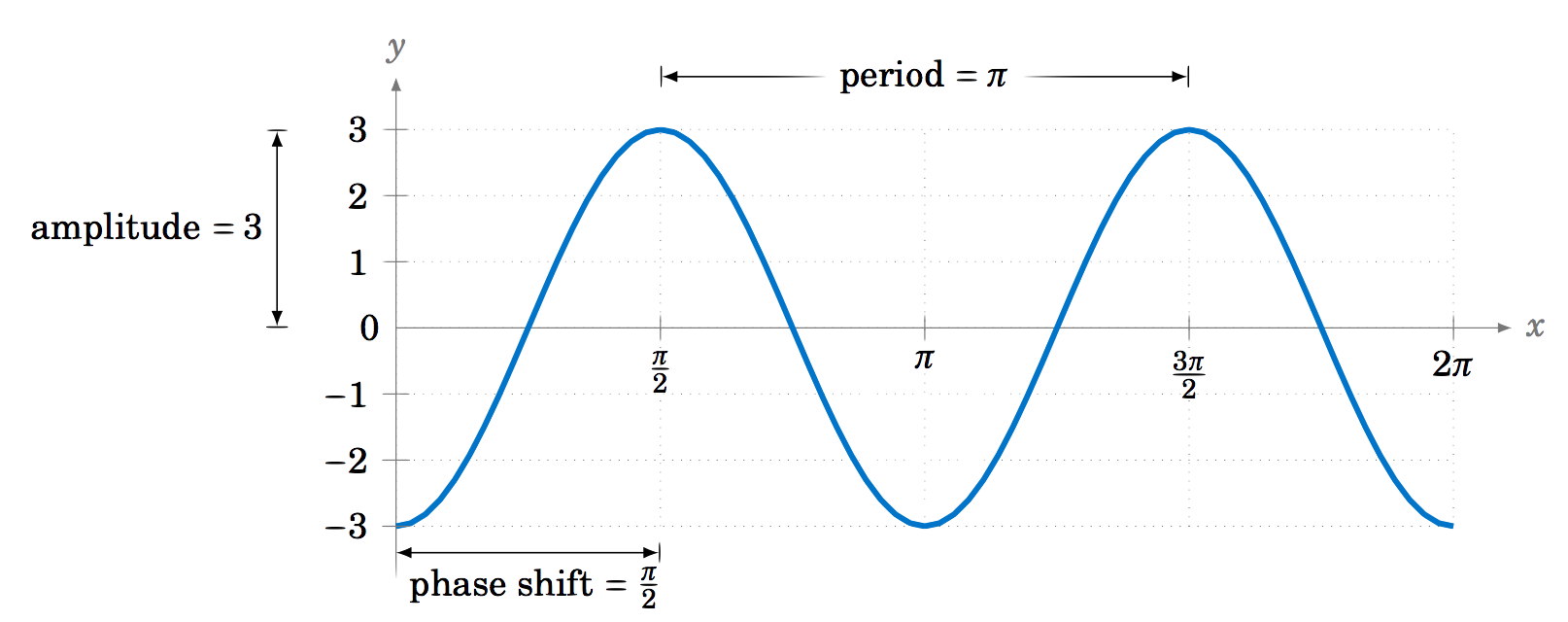
Notice that the graph is the same as the graph of y=3cos2x shifted to the right by π2, the amount of the phase shift.
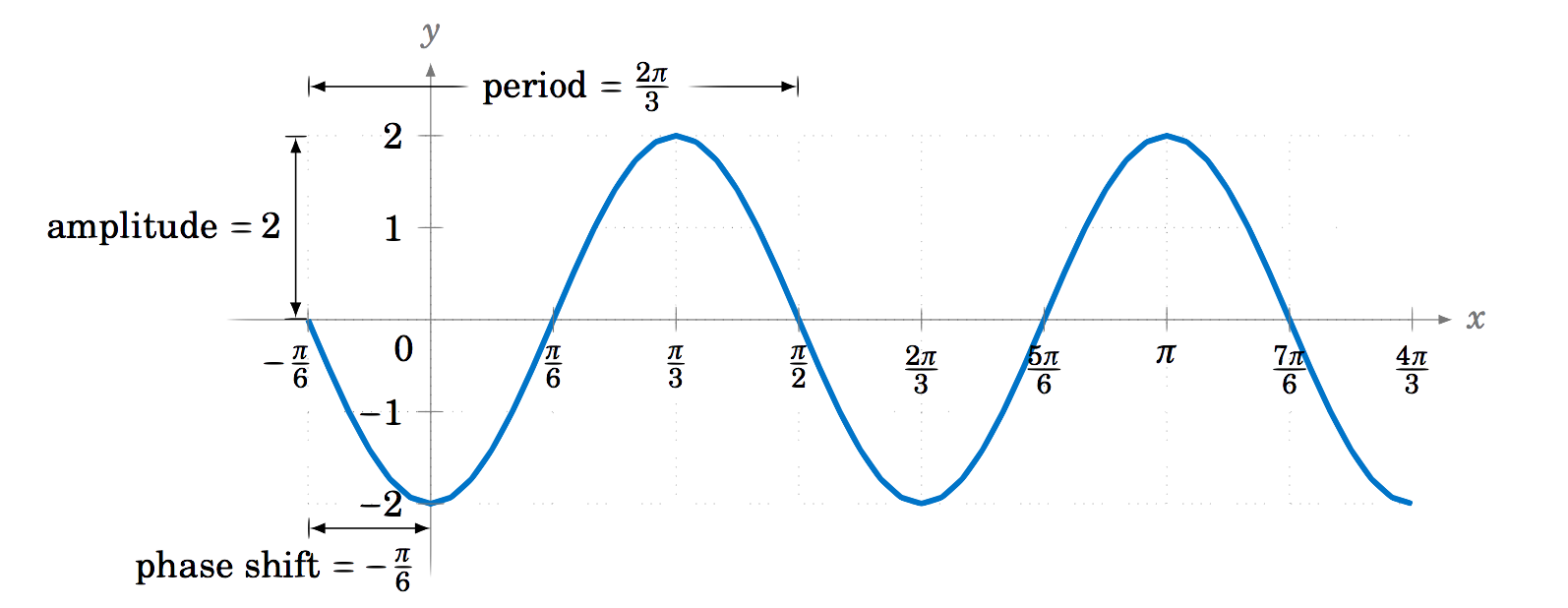
Find the amplitude, period, and phase shift of y=−2sin(3x+π2).
Solution
The amplitude is 2, the period is 2π3, and the phase shift is −π23=−π6. Notice the negative sign in the phase shift, since 3x+π=3x−(−π) is in the form ωx−ϕ. The graph is shown in Figure 5.2.13:
In engineering two periodic functions with the same period are said to be out of phase if their phase shifts differ. For example, sin(x−π6) and sinx would be π6 radians (or 30∘) out of phase, and sinx would be said to lag sin(x−π6) by π6 radians, while sin(x−π6) leads \(\sin\;x \) by π6 radians. Periodic functions with the same period and the same phase shift are in phase.
The following is a summary of the properties of trigonometric graphs:
For any constants A≠0, ω≠0, and ϕ:
y=Asin(ωx−ϕ) has amplitude |A|, period 2πω, and phase shift ϕωy=Acos(ωx−ϕ) has amplitude |A|, period 2πω, and phase shift ϕωy=Atan(ωx−ϕ) has undefined amplitude, period πω, and phase shift ϕωy=Acsc(ωx−ϕ) has undefined amplitude, period 2πω, and phase shift ϕωy=Asec(ωx−ϕ) has undefined amplitude, period 2πω, and phase shift ϕωy=Acot(ωx−ϕ) has undefined amplitude, period πω, and phase shift ϕω



