11.7: Probability
- Last updated
- Save as PDF
- Page ID
- 1402
Learning Objectives
- Construct probability models.
- Compute probabilities of equally likely outcomes.
- Compute probabilities of the union of two events.
- Use the complement rule to find probabilities.
- Compute probability using counting theory.
Residents of the Southeastern United States are all too familiar with charts, known as spaghetti models, such as the one in Figure \(\PageIndex{1}\). They combine a collection of weather data to predict the most likely path of a hurricane. Each colored line represents one possible path. The group of squiggly lines can begin to resemble strands of spaghetti, hence the name. In this section, we will investigate methods for making these types of predictions.
Figure \(\PageIndex{1}\): An example of a “spaghetti model,” which can be used to predict possible paths of a tropical storm.1
Constructing Probability Models
Suppose we roll a six-sided number cube. Rolling a number cube is an example of an experiment, or an activity with an observable result. The numbers on the cube are possible results, or outcomes, of this experiment. The set of all possible outcomes of an experiment is called the sample space of the experiment. The sample space for this experiment is \(\{1,2,3,4,5,6 \}\). An event is any subset of a sample space.
The likelihood of an event is known as probability. The probability of an event pp is a number that always satisfies \(0≤p≤1\), where \(0\) indicates an impossible event and \(1\) indicates a certain event. A probability model is a mathematical description of an experiment listing all possible outcomes and their associated probabilities. For instance, if there is a \(1\%\) chance of winning a raffle and a \(99\%\) chance of losing the raffle, a probability model would look much like Table \(\PageIndex{1}\).
| Outcome | Probability |
|---|---|
| Winning the raffle | 1% |
| Losing the raffle | 99% |
The sum of the probabilities listed in a probability model must equal \(1\), or \(100\%\).
How to: Given a probability event where each event is equally likely, construct a probability model.
- Identify every outcome.
- Determine the total number of possible outcomes.
- Compare each outcome to the total number of possible outcomes.
Example \(\PageIndex{1}\): Constructing a Probability Model
Construct a probability model for rolling a single, fair die, with the event being the number shown on the die.
Solution
Begin by making a list of all possible outcomes for the experiment. The possible outcomes are the numbers that can be rolled: \(1\), \(2\), \(3\), \(4\), \(5\), and \(6\). There are six possible outcomes that make up the sample space.
Assign probabilities to each outcome in the sample space by determining a ratio of the outcome to the number of possible outcomes. There is one of each of the six numbers on the cube, and there is no reason to think that any particular face is more likely to show up than any other one, so the probability of rolling any number is \(16\).
| Outcome | Roll of 1 | Roll of 2 | Roll of 3 | Roll of 4 | Roll of 5 | Roll of 6 |
|---|---|---|---|---|---|---|
| Probability | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Q&A: Do probabilities always have to be expressed as fractions?
No. Probabilities can be expressed as fractions, decimals, or percents. Probability must always be a number between \(0\) and \(1\), inclusive of \(0\) and \(1\).
Computing Probabilities of Equally Likely Outcomes
Let \(S\) be a sample space for an experiment. When investigating probability, an event is any subset of \(S\). When the outcomes of an experiment are all equally likely, we can find the probability of an event by dividing the number of outcomes in the event by the total number of outcomes in \(S\). Suppose a number cube is rolled, and we are interested in finding the probability of the event “rolling a number less than or equal to 4.” There are 4 possible outcomes in the event and 6 possible outcomes in \(S\), so the probability of the event is \(\dfrac{4}{6}=\dfrac{2}{3}\).
COMPUTING THE PROBABILITY OF AN EVENT WITH EQUALLY LIKELY OUTCOMES
The probability of an event \(E\) in an experiment with sample space \(S\) with equally likely outcomes is given by
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\) is a subset of \(S\), so it is always true that \(0≤P(E)≤1\).
Example \(\PageIndex{2}\): Computing the Probability of an Event with Equally Likely Outcomes
A number cube is rolled. Find the probability of rolling an odd number.
Solution
The event “rolling an odd number” contains three outcomes. There are \(6\) equally likely outcomes in the sample space. Divide to find the probability of the event.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Exercise \(\PageIndex{1}\)
A number cube is rolled. Find the probability of rolling a number greater than \(2\).
- Answer
-
\(\dfrac{2}{3}\)
Computing the Probability of the Union of Two Events
We are often interested in finding the probability that one of multiple events occurs. Suppose we are playing a card game, and we will win if the next card drawn is either a heart or a king. We would be interested in finding the probability of the next card being a heart or a king. The union of two events \(E\) and \(F\),written \(E\cup F\), is the event that occurs if either or both events occur.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Suppose the spinner in Figure \(\PageIndex{2}\) is spun. We want to find the probability of spinning orange or spinning a \(b\).
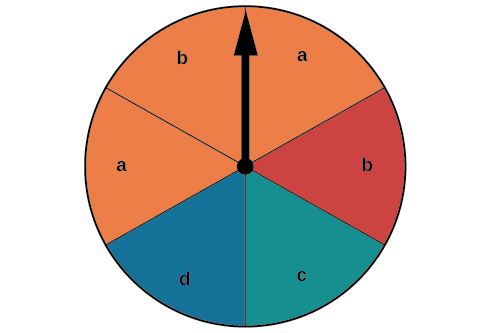
Figure \(\PageIndex{2}\): A pie chart with six options.
There are a total of \(6\) sections, and \(3\) of them are orange. So the probability of spinning orange is \(\dfrac{3}{6}=\dfrac{1}{2}\). There are a total of \(6\) sections, and \(2\) of them have a \(b\). So the probability of spinning a \(b\) is \(\dfrac{2}{6}=\dfrac{1}{3}\). If we added these two probabilities, we would be counting the sector that is both orange and a \(b\) twice. To find the probability of spinning an orange or a \(b\), we need to subtract the probability that the sector is both orange and has a \(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
The probability of spinning orange or a \(b\) is \(\dfrac{2}{3}\).
PROBABILITY OF THE UNION OF TWO EVENTS
The probability of the union of two events \(E\) and \(F\) (written \(E\cup F\)) equals the sum of the probability of \(E\) and the probability of \(F\) minus the probability of \(E\) and \(F\) occurring together (which is called the intersection of \(E\) and \(F\) and is written as \(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Example \(\PageIndex{3}\): Computing the Probability of the Union of Two Events
A card is drawn from a standard deck. Find the probability of drawing a heart or a \(7\).
Solution
A standard deck contains an equal number of hearts, diamonds, clubs, and spades. So the probability of drawing a heart is \(\dfrac{1}{4}\). There are four \(7s\) in a standard deck, and there are a total of \(52\) cards. So the probability of drawing a \(7\) is \(\dfrac{1}{13}\).
The only card in the deck that is both a heart and a \(7\) is the \(7\) of hearts, so the probability of drawing both a heart and a \(7\) is \(\dfrac{1}{52}\). Substitute \(P(H)=\dfrac{1}{4}\), \(P(7)=\dfrac{1}{13}\), and \(P(H\cap 7)=\dfrac{1}{52}\) into the formula.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
The probability of drawing a heart or a \(7\) is \(\dfrac{4}{13}\).
Exercise \(\PageIndex{2}\)
A card is drawn from a standard deck. Find the probability of drawing a red card or an ace.
- Answer
-
\(\dfrac{7}{13}\)
Computing the Probability of Mutually Exclusive Events
Suppose the spinner in Figure \(\PageIndex{2}\) is spun again, but this time we are interested in the probability of spinning an orange or a \(d\). There are no sectors that are both orange and contain a \(d\), so these two events have no outcomes in common. Events are said to be mutually exclusive events when they have no outcomes in common. Because there is no overlap, there is nothing to subtract, so the general formula is
\[P(E\cap F)=P(E)+P(F)\]
Notice that with mutually exclusive events, the intersection of \(E\) and \(F\) is the empty set. The probability of spinning an orange is \(\dfrac{3}{6}=\dfrac{1}{2}\) and the probability of spinning a \(d\) is \(\dfrac{1}{6}\). We can find the probability of spinning an orange or a \(d\) simply by adding the two probabilities.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
The probability of spinning an orange or a \(d\) is \(\dfrac{2}{3}\).
PROBABILITY OF THE UNION OF MUTUALLY EXCLUSIVE EVENTS
The probability of the union of two mutually exclusive events \(E\) and \(F\) is given by
\[P(E\cap F)=P(E)+P(F)\]
How to: Given a set of events, compute the probability of the union of mutually exclusive events.
- Determine the total number of outcomes for the first event.
- Find the probability of the first event.
- Determine the total number of outcomes for the second event.
- Find the probability of the second event.
- Add the probabilities.
Example \(\PageIndex{4}\): Computing the Probability of the Union of Mutually Exclusive Events
A card is drawn from a standard deck. Find the probability of drawing a heart or a spade.
Solution
The events “drawing a heart” and “drawing a spade” are mutually exclusive because they cannot occur at the same time. The probability of drawing a heart is \(\dfrac{1}{4}\), and the probability of drawing a spade is also \(\dfrac{1}{4}\), so the probability of drawing a heart or a spade is
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
Exercise \(\PageIndex{3}\)
A card is drawn from a standard deck. Find the probability of drawing an ace or a king.
- Answer
-
\(\dfrac{2}{13}\)
Using the Complement Rule to Compute Probabilities
We have discussed how to calculate the probability that an event will happen. Sometimes, we are interested in finding the probability that an event will not happen. The complement of an event \(E\), denoted \(E′\), is the set of outcomes in the sample space that are not in \(E\). For example, suppose we are interested in the probability that a horse will lose a race. If event \(W\) is the horse winning the race, then the complement of event \(W\) is the horse losing the race.
To find the probability that the horse loses the race, we need to use the fact that the sum of all probabilities in a probability model must be \(1\).
\[P(E′)=1−P(E)\]
The probability of the horse winning added to the probability of the horse losing must be equal to \(1\). Therefore, if the probability of the horse winning the race is \(\dfrac{1}{9}\), the probability of the horse losing the race is simply
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
THE COMPLEMENT RULE
The probability that the complement of an event will occur is given by
\[P(E′)=1−P(E)\]
Example \(\PageIndex{5}\): Using the Complement Rule to Calculate Probabilities
Two six-sided number cubes are rolled.
- Find the probability that the sum of the numbers rolled is less than or equal to \(3\).
- Find the probability that the sum of the numbers rolled is greater than \(3\).
Solution
The first step is to identify the sample space, which consists of all the possible outcomes. There are two number cubes, and each number cube has six possible outcomes. Using the Multiplication Principle, we find that there are \(6×6\), or \(36\) total possible outcomes. So, for example, \(1-1\) represents a \(1\) rolled on each number cube.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- We need to count the number of ways to roll a sum of \(3\) or less. These would include the following outcomes: \(1-1\), \(1-2\), and \(2-1\). So there are only three ways to roll a sum of \(3\) or less. The probability is
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- Rather than listing all the possibilities, we can use the Complement Rule. Because we have already found the probability of the complement of this event, we can simply subtract that probability from \(1\) to find the probability that the sum of the numbers rolled is greater than \(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Exercise \(\PageIndex{4}\):
Two number cubes are rolled. Use the Complement Rule to find the probability that the sum is less than \(10\).
- Answer
-
\(\dfrac{5}{6}\)
Computing Probability Using Counting Theory
Many interesting probability problems involve counting principles, permutations, and combinations. In these problems, we will use permutations and combinations to find the number of elements in events and sample spaces. These problems can be complicated, but they can be made easier by breaking them down into smaller counting problems.
Assume, for example, that a store has \(8\) cellular phones and that \(3\) of those are defective. We might want to find the probability that a couple purchasing \(2\) phones receives \(2\) phones that are not defective. To solve this problem, we need to calculate all of the ways to select \(2\) phones that are not defective as well as all of the ways to select \(2\) phones. There are \(5\) phones that are not defective, so there are \(C(5,2)\) ways to select \(2\) phones that are not defective. There are \(8\) phones, so there are \(C(8,2)\) ways to select \(2\) phones. The probability of selecting \(2\) phones that are not defective is:
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Example \(\PageIndex{5}\): Computing Probability Using Counting Theory
A child randomly selects \(5\) toys from a bin containing \(3\) bunnies, \(5\) dogs, and \(6\) bears.
- Find the probability that only bears are chosen.
- Find the probability that \(2\) bears and \(3\) dogs are chosen.
- Find the probability that at least \(2\) dogs are chosen.
Solution
- We need to count the number of ways to choose only bears and the total number of possible ways to select \(5\) toys. There are \(6\) bears, so there are \(C(6,5)\) ways to choose \(5\) bears. There are \(14\) toys, so there are \(C(14,5)\) ways to choose any \(5\) toys.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- We need to count the number of ways to choose \(2\) bears and \(3\) dogs and the total number of possible ways to select \(5\) toys. There are \(6\) bears, so there are \(C(6,2)\) ways to choose \(2\) bears. There are \(5\) dogs, so there are \(C(5,3)\) ways to choose \(3\) dogs. Since we are choosing both bears and dogs at the same time, we will use the Multiplication Principle. There are \(C(6,2)⋅C(5,3)\) ways to choose \(2\) bears and \(3\) dogs. We can use this result to find the probability.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- It is often easiest to solve “at least” problems using the Complement Rule. We will begin by finding the probability that fewer than \(2\) dogs are chosen. If less than \(2\) dogs are chosen, then either no dogs could be chosen, or \(1\) dog could be chosen.
When no dogs are chosen, all \(5\) toys come from the \(9\) toys that are not dogs. There are \(C(9,5)\) ways to choose toys from the \(9\) toys that are not dogs. Since there are \(14\) toys, there are \(C(14,5)\) ways to choose the \(5\) toys from all of the toys.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
If there is \(1\) dog chosen, then \(4\) toys must come from the \(9\) toys that are not dogs, and \(1\) must come from the \(5\) dogs. Since we are choosing both dogs and other toys at the same time, we will use the Multiplication Principle. There are \(C(5,1)⋅C(9,4)\) ways to choose \(1\) dog and \(1\) other toy.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Because these events would not occur together and are therefore mutually exclusive, we add the probabilities to find the probability that fewer than \(2\) dogs are chosen.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
We then subtract that probability from \(1\) to find the probability that at least \(2\) dogs are chosen.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
Exercise \(\PageIndex{5}\)
A child randomly selects \(3\) gumballs from a container holding \(4\) purple gumballs, \(8\) yellow gumballs, and \(2\) green gumballs.
- Find the probability that all \(3\) gumballs selected are purple.
- Find the probability that no yellow gumballs are selected.
- Find the probability that at least \(1\) yellow gumball is selected.
- Answer
-
\(\dfrac{1}{91}\)
- Answer
-
\(\dfrac{5}{91}\)
- Answer
-
\(\dfrac{86}{91}\)
Media
Access these online resources for additional instruction and practice with probability.
Visit this website for additional practice questions from Learningpod.
Key Equations
| probability of an event with equally likely outcomes | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| probability of the union of two events | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| probability of the union of mutually exclusive events | \(P(E\cup F)=P(E)+P(F)\) |
| probability of the complement of an event | \(P(E')=1−P(E)\) |
Key Concepts
- Probability is always a number between \(0\) and \(1\), where \(0\) means an event is impossible and \(1\) means an event is certain.
- The probabilities in a probability model must sum to \(1\). See Example \(\PageIndex{1}\).
- When the outcomes of an experiment are all equally likely, we can find the probability of an event by dividing the number of outcomes in the event by the total number of outcomes in the sample space for the experiment. See Example \(\PageIndex{2}\).
- To find the probability of the union of two events, we add the probabilities of the two events and subtract the probability that both events occur simultaneously. See Example \(\PageIndex{3}\).
- To find the probability of the union of two mutually exclusive events, we add the probabilities of each of the events. See Example \(\PageIndex{4}\).
- The probability of the complement of an event is the difference between \(1\) and the probability that the event occurs. See Example \(\PageIndex{5}\).
- In some probability problems, we need to use permutations and combinations to find the number of elements in events and sample spaces. See Example \(\PageIndex{6}\).
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


