11.E: Sequences, Probability and Counting Theory (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
11.1 Sequences and Their Notations
Verbal
1) Discuss the meaning of a sequence. If a finite sequence is defined by a formula, what is its domain? What about an infinite sequence?
- Answer
-
A sequence is an ordered list of numbers that can be either finite or infinite in number. When a finite sequence is defined by a formula, its domain is a subset of the non-negative integers. When an infinite sequence is defined by a formula, its domain is all positive or all non-negative integers.
2) Describe three ways that a sequence can be defined.
3) Is the ordered set of even numbers an infinite sequence? What about the ordered set of odd numbers? Explain why or why not.
- Answer
-
Yes, both sets go on indefinitely, so they are both infinite sequences.
4) What happens to the terms an of a sequence when there is a negative factor in the formula that is raised to a power that includes n? What is the term used to describe this phenomenon?
5) What is a factorial, and how is it denoted? Use an example to illustrate how factorial notation can be beneficial.
- Answer
-
A factorial is the product of a positive integer and all the positive integers below it. An exclamation point is used to indicate the operation. Answers may vary. An example of the benefit of using factorial notation is when indicating the product It is much easier to write than it is to write out 13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1
Algebraic
For the exercises 6-15, write the first four terms of the sequence.
6) an=2n−2
7) an=−16n+1
- Answer
-
First four terms: −8, −163, −4, −165
8) an=−(−5)n−1
9) an=2nn3
- Answer
-
First four terms: 2, 12, 827, 14
10) an=2n+1n3
11) an=1.25⋅(−4)n−1
- Answer
-
First four terms: 1.25, −5, 20, −80
12) an=−4⋅(−6)n−1
13) an=n22n+1
- Answer
-
First four terms: 13, 45, 97, 169
14) an=(−10)n+1
15) an=−(4⋅(−5)n−15)
- Answer
-
First four terms: −45, 4, −20, 100
For the exercises 16-20, write the first eight terms of the piecewise sequence.
16) an={(−2)n−2 if n is even(3)n−1 if n is odd
17) an={n22n+1 if n≤5n2−5 if n>5
- Answer
-
13,45,97,169,2511,31,44,59
18) an={(2n+1)2 if n is divisible by 42n if n is not divisible by 4
19) an={−0.6⋅5n−1 if n is prime or 12.5⋅(−2)n−1 if n is composite
- Answer
-
−0.6,−3,−15,−20,−375,−80,−9375,−320
20) an={4(n2−2) if n≤3 or n>6n2−24 if 3<n≤6
For the exercises 21-25, write an explicit formula for each sequence.
21) 4,7,12,19,28,…
- Answer
-
an=n2+3
22) −4,2,−10,14,−34,…
23) 1,1,43,2,165,…
- Answer
-
an=2n2n or 2n−1n
24) 0,1−e11+e2,1−e21+e3,1−e31+e4,1−e41+e5,…
25) 1,−12,14,−18,116,…
- Answer
-
an=(−12)n−1
For the exercises 26-30, write the first five terms of the sequence.
26) a1=9,an=an−1+n
27) a1=3,an=(−3)an−1
- Answer
-
First five terms: 3,−9,27,−81,243
28) a1=−4,an=an−1+2nan−1−1
29) a1=−1,an=(−3)n−1an−1−2
- Answer
-
First five terms: −1,1,−9,2711,8915
30) a1=−30,an=(2+an−1)(12)n
For the exercises 31-33, write the first eight terms of the sequence.
31) a1=124,a2=1,an=(2an−2)(3an−1)
- Answer
-
124,1,14,32,94,814,21878,531,44116
32) a1=−1,a2=5,an=an−2(3−an−1)
33) a1=2,a2=10,an=2(an−1+2)an−2
- Answer
-
2,10,12,145,45,2,10,12
For the exercises 34-38, write a recursive formula for each sequence.
34) −2.5,−5,−10,−20,−40,…
35) −8,−6,−3,1,6,…
- Answer
-
a1=−8,an=an−1+n
36) 2,4,12,48,240,…
37) 35,38,41,44,47,…
- Answer
-
a1=35,an=an−1+3
38) 15,3,35,325,3125,…
For the exercises 39-42, evaluate the factorial.
39) 6!
- Answer
-
720
40) (126)!
41) 12!6!
- Answer
-
665,280
42) 100!99!
For the exercises 43-46, write the first four terms of the sequence.
43) an=n!n2
- Answer
-
First four terms: 1, 12, 23, 32
44) an=3⋅n!4⋅n!
45) an=n!n2−n−1
- Answer
-
First four terms: -1, 2, 65, 2411
46) an=100⋅nn(n−1)!
Graphical
For the exercises 47-51, graph the first five terms of the indicated sequence
47) an=(−1)nn+n
- Answer
-
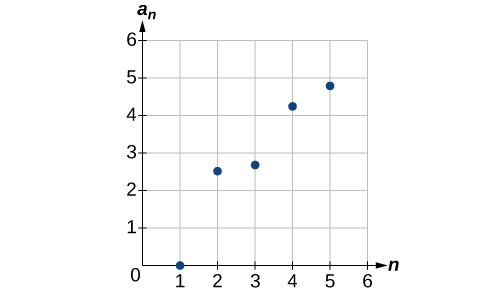
48) an={4+n2n if n is even 3+n if if n is odd
49) a1=2,an=(−an−1+1)2
- Answer
-
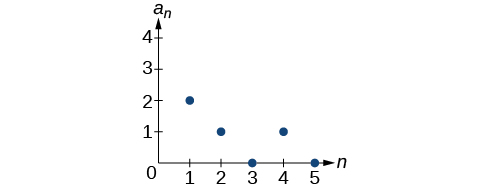
50) an=1,an=an−1+8
51) an=(n+1)!(n−1)!
- Answer
-
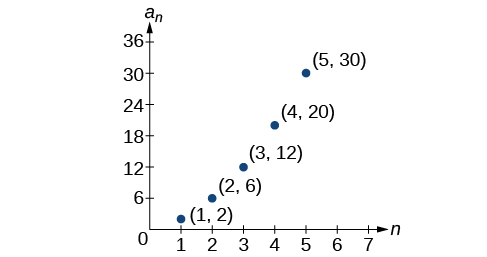
For the exercises 52-54, write an explicit formula for the sequence using the first five points shown on the graph.
52)
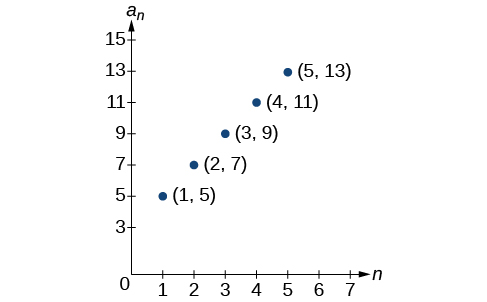
53)
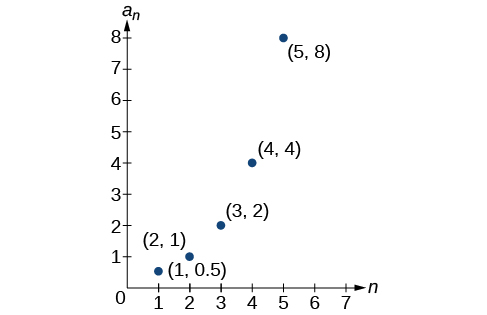
- Answer
-
an=2n−2
54)
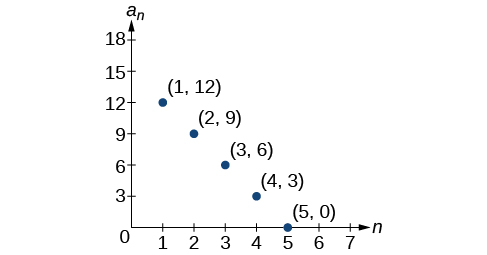
For the exercises 55-56, write a recursive formula for the sequence using the first five points shown on the graph.
55)
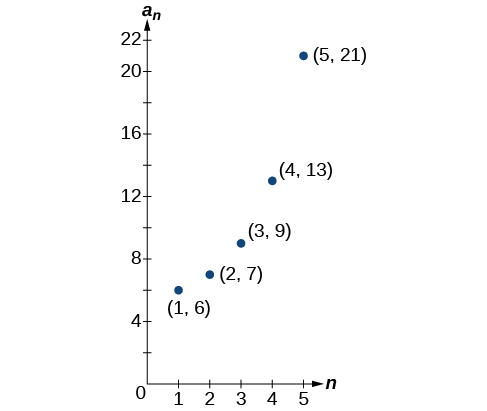
- Answer
-
a1=6,an=2an−1−5
56)
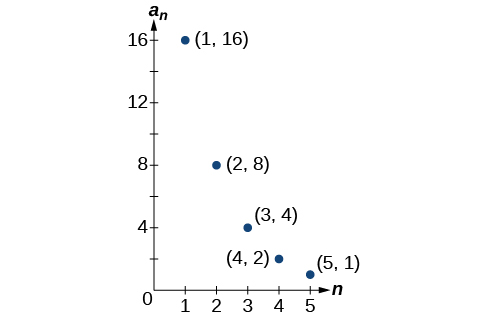
Technology
Follow these steps to evaluate a sequence defined recursively using a graphing calculator:
- On the home screen, key in the value for the initial term a1 and press [ENTER].
- Enter the recursive formula by keying in all numerical values given in the formula, along with the key strokes [2ND] ANS for the previous term an−1. Press [ENTER].
- Continue pressing [ENTER] to calculate the values for each successive term.
For the exercises 57-61, use the steps above to find the indicated term or terms for the sequence.
57) Find the first five terms of the sequence a1=87111, an=43an−1+1237. Use the >Frac feature to give fractional results.
- Answer
-
First five terms: 2937,152111,716333,3188999,137242997
58) Find the 15th term of the sequence a1=625,an=0.8an−1+18.
59) Find the first five terms of the sequence a1=2,an=2[(an−1)−1]+1.
- Answer
-
First five terms: 2,3,5,17,65537
60) Find the first ten terms of the sequence a1=8,an=(an−1+1)!an−1!.
61) Find the tenth term of the sequence a1=2,an=nan−1.
- Answer
-
a10=7,257,600
Follow these steps to evaluate a finite sequence defined by an explicit formula. Using a TI-84, do the following.
- In the home screen, press [2ND] LIST.
- Scroll over to OPS and choose “seq(” from the dropdown list. Press [ENTER].
- In the line headed “Expr:” type in the explicit formula, using the [X,T,θ,n] button for n
- In the line headed “Variable:” type in the variable used on the previous step.
- In the line headed “start:” key in the value of n
n n - In the line headed “end:” key in the value of n
n n - Press [ENTER] 3 times to return to the home screen. You will see the sequence syntax on the screen. Press [ENTER] to see the list of terms for the finite sequence defined. Use the right arrow key to scroll through the list of terms.
Using a TI-83, do the following.
- In the home screen, press [2ND] LIST.
- Scroll over to OPS and choose “seq(” from the dropdown list. Press [ENTER].
- Enter the items in the order “Expr”, “Variable”, “start”, “end” separated by commas. See the instructions above for the description of each item.
- Press [ENTER] to see the list of terms for the finite sequence defined. Use the right arrow key to scroll through the list of terms.
For the exercises 62-66, use the steps above to find the indicated terms for the sequence. Round to the nearest thousandth when necessary.
62) List the first five terms of the sequence an=−289n+53.
63) List the first six terms of the sequence an=n3−3.5n2+4.1n−1.52.4n.
- Answer
-
First six terms: 0.042,0.146,0.875,2.385,4.708
64) List the first five terms of the sequence an=15n⋅(−2)n−147.
65) List the first four terms of the sequence an=5.7n+0.275(n−1)!
- Answer
-
First four terms: 5.975,32.765,185.743,1057.25,6023.521
66) List the first six terms of the sequence an=n!n.
Extensions
67) Consider the sequence defined by an=−6−8n. Is an=−421 a term in the sequence? Verify the result.
- Answer
-
If an=−421 is a term in the sequence, then solving the equation −421=−6−8n for n will yield a non-negative integer. However, if −421=−6−8n,
68) What term in the sequence an=n2+4n+42(n+2) has the value 41? Verify the result.
69) Find a recursive formula for the sequence 1,0,−1,−1,0,1,1,0,−1,−1,0,1,1,… (Hint: find a pattern for an based on the first two terms.)
- Answer
-
a1=1,a2=0,an=an−1−an−2
70) Calculate the first eight terms of the sequences an=(n+2)!(n−1)! and bn=n3+3n2+2n, and then make a conjecture about the relationship between these two sequences.
71) Prove the conjecture made in the preceding exercise.
- Answer
-
(n+2)!(n−1)!=(n+2)⋅(n+1)⋅(n)⋅(n−1)⋅…3⋅2⋅1(n−1)⋅…3⋅2⋅1=n(n+1)(n+2)=n3+3n2+2n
11.2 Arithmetic Sequences
Verbal
1) What is an arithmetic sequence?
- Answer
-
A sequence where each successive term of the sequence increases (or decreases) by a constant value.
2) How is the common difference of an arithmetic sequence found?
3) How do we determine whether a sequence is arithmetic?
- Answer
-
We find whether the difference between all consecutive terms is the same. This is the same as saying that the sequence has a common difference.
4) What are the main differences between using a recursive formula and using an explicit formula to describe an arithmetic sequence?
5) Describe how linear functions and arithmetic sequences are similar. How are they different?
- Answer
-
Both arithmetic sequences and linear functions have a constant rate of change. They are different because their domains are not the same; linear functions are defined for all real numbers, and arithmetic sequences are defined for natural numbers or a subset of the natural numbers.
Algebraic
For the exercises 6-7, find the common difference for the arithmetic sequence provided.
6) {5,11,17,23,29,...}
7) {0,12,1,32,2,...}
- Answer
-
The common difference is 12
For the exercises 8-9, determine whether the sequence is arithmetic. If so find the common difference.
8) {11.4,9.3,7.2,5.1,3,...}
9) {4,16,64,256,1024,...}
- Answer
-
The sequence is not arithmetic because 16−4≠64−16
For the exercises 10-11, write the first five terms of the arithmetic sequence given the first term and common difference.
10) a1=−25,d=−9
11) a1=0,d=23
- Answer
-
0,23,43,2,83
For the exercises 12-13, write the first five terms of the arithmetic series given two terms.
12) a1=17,a7=−31
13) a13=−60,a33=−160
- Answer
-
0,−5,−10,−15,−20
For the exercises 14-18, find the specified term for the arithmetic sequence given the first term and common difference.
14) First term is 3, common difference is 4, find the 5th term.
15) First term is 4, common difference is 5, find the 4th term.
- Answer
-
a4=19
16) First term is 5, common difference is 6, find the 8th term.
17) First term is 6, common difference is 7, find the 6th term.
- Answer
-
a6=41
18) First term is 7, common difference is 8, find the 7th term.
For the exercises 19-23, find the first term given two terms from an arithmetic sequence.
19) Find the first term or a1 of an arithmetic sequence if a6=12 and a14=28.
- Answer
-
a1=2
20) Find the first term or a1 of an arithmetic sequence if a7=21 and a15=42.
21) Find the first term or a1 of an arithmetic sequence if a8=40 and a123=115.
- Answer
-
a1=5
22) Find the first term or a1 of an arithmetic sequence if a9=54 and a17=102.
23) Find the first term or a1 of an arithmetic sequence if a11=11 and a21=16.
- Answer
-
a1=6
For the exercises 24-25, find the specified term given two terms from an arithmetic sequence.
24) a1=33 and a7=−15. Find a4.
25) a3=−17.1 and a10=−15.7. Find a21.
- Answer
-
a21=−13.5
For the exercises 26-27, use the recursive formula to write the first five terms of the arithmetic sequence.
26) a1=39;an=an−1−3
27) a1=−19;an=an−1−1.4
- Answer
-
−19,−20.4,−21.8,−23.2,−24.6
For the exercises 28-37, write a recursive formula for each arithmetic sequence.
28) a={40,60,80,...}
29) a={17,26,35,...}
- Answer
-
a1=17;an=an−1+9,n≥2
30) a={−1,2,5,...}
31) a={12,17,22,...}
- Answer
-
a1=12;an=an−1+5,n≥2
32) a={−15,−7,1,...}
33) a={8.9,10.3,11.7,...}
- Answer
-
a1=8.9;an=an−1+1.4,n≥2
34) a={−0.52,−1.02,−1.52,...}
35) a={15,920,710,...}
- Answer
-
a1=15;an=an−1+14,n≥2
36) a={−12,−54,−2,...}
37) a={16,−1112,−2,...}
- Answer
-
a1=16;an=an−1−1312,n≥2
For the exercises 38-40, write a recursive formula for the given arithmetic sequence, and then find the specified term.
38) a={7,4,1,...}; Find the 17th term.
39) a={4,11,18,...}; Find the 14th term.
- Answer
-
a1=4;an=an−1+7,a14=95
40) a={2,6,10,...}; Find the 12th term.
For the exercises 41-42, use the explicit formula to write the first five terms of the arithmetic sequence.
41) an=24−4n
- Answer
-
First five terms: 20,16,12,8,4.
42) an=12n−12
For the exercises 43-52, write an explicit formula for each arithmetic sequence.
43) a={3,5,7,...}
- Answer
-
an=1+2n
44) a={32,24,16,...}
45) a={−5,95,195,...}
- Answer
-
an=−105+100n
46) a={−17,−217,−417,...}
47) a={1.8,3.6,5.4,...}
- Answer
-
an=1.8n
48) a={−18.1,−16.2,−14.3,...}
49) a={15.8,18.5,21.2,...}
- Answer
-
an=13.1+2.7n
50) a={13,−43,−3,...}
51) a={0,13,23,...}
- Answer
-
an=13n−13
52) a={−5,−103,−53,...}
For the exercises 53-55, find the number of terms in the given finite arithmetic sequence.
53) a={3,−4,−11,...,−60}
- Answer
-
There are 10 terms in the sequence.
54) a={1.2,1.4,1.6,...,3.8}
55) a={12,2,72,...,8}
- Answer
-
There are 6 terms in the sequence.
Graphical
For the exercises 56-57, determine whether the graph shown represents an arithmetic sequence.
56)
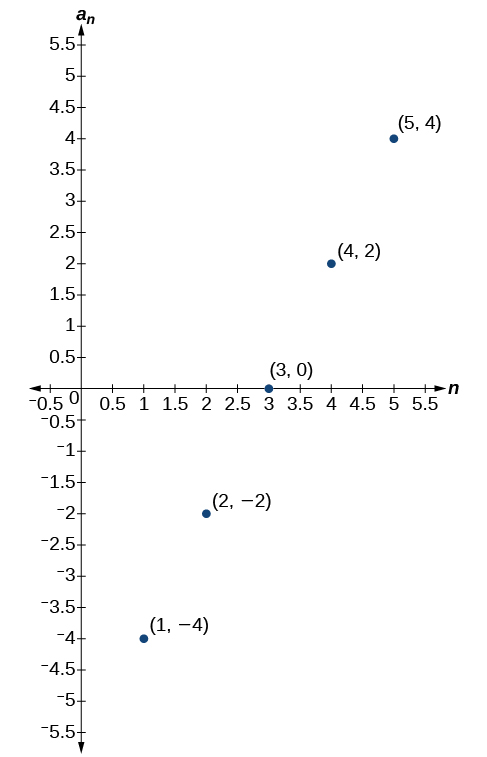
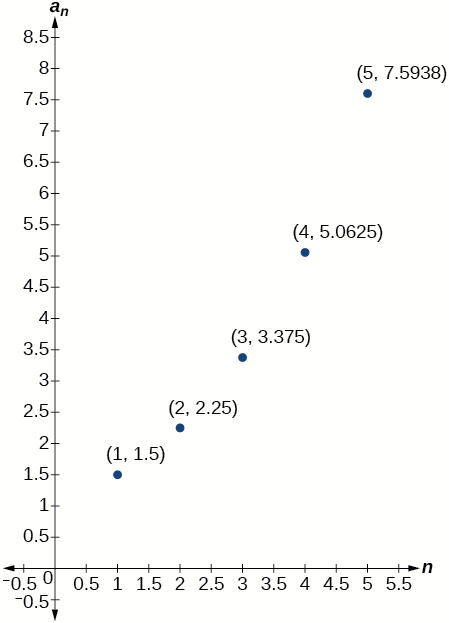
57)
- Answer
-
The graph does not represent an arithmetic sequence.
For the exercises 58-60, use the information provided to graph the first 5 terms of the arithmetic sequence.
58) a1=0,d=4
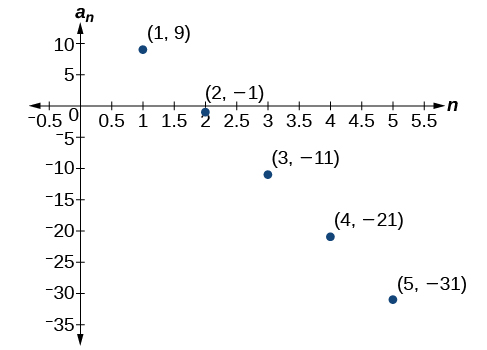
59) a1=9,an=an−1−10
- Answer
-
60) an=−12+5n
Technology
For the exercises 61-63, follow the steps to work with the arithmetic sequence an=3n−2 using a graphing calculator:
- Press [MODE]
- Select SEQ in the fourth line
- Select DOT in the fifth line
- Press [ENTER]
- Press [Y=]
- nMin is the first counting number for the sequence. Set nMin=1
- u(n is the pattern for the sequence. Set u(n)=3n−2
- u(nMin) is the first number in the sequence. Set u(nMin)=1
- Press [2ND] then [WINDOW] to go to TBLSET
- Set TblStart=1
- Set ΔTbl=1
- Set Indpnt: Auto and Depend: Auto
- Press [2ND] then [GRAPH] to go to the TABLE
61) What are the first seven terms shown in the column with the heading u(n)?
- Answer
-
1,4,7,10,13,16,19
62) Use the scroll-down arrow to scroll to n=50
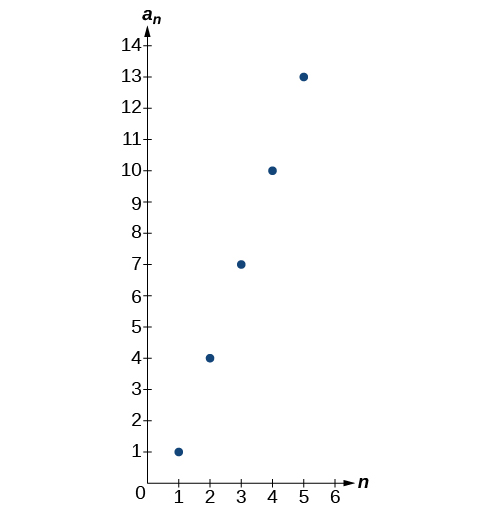
63) Press [WINDOW]. Set nMin=1,nMax=5,xMin=0,xMax=6,yMin=−1,yMax=14. Then press [GRAPH]. Graph the sequence as it appears on the graphing calculator.
- Answer
-
For the exercises 64-65, follow the steps given above to work with the arithmetic sequence an=12n+5 using a graphing calculator.
64) What are the first seven terms shown in the column with the heading u(n) in the TABLE feature?
65) Graph the sequence as it appears on the graphing calculator. Be sure to adjust the WINDOW settings as needed.
- Answer
-
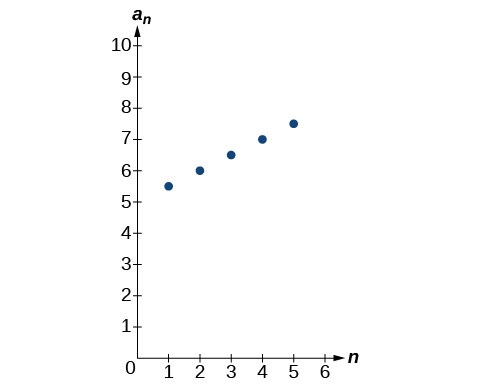
Extensions
66) Give two examples of arithmetic sequences whose 4th terms are 9.
67) Give two examples of arithmetic sequences whose 10th terms are 206.
- Answer
-
Answers will vary. Examples: an=20.6n and an=2+20.4n.
68) Find the 5th term of the arithmetic sequence {9b,5b,b,...}.
69) Find the \(11^{th}\) term of the arithmetic sequence {3a−2b,a+2b,−a+6b...}
- Answer
-
a11=−17a+38b
70) At which term does the sequence {5.4,14.5,23.6,...} exceed 151?
71) At which term does the sequence {173,316,143,...} begin to have negative values?
- Answer
-
The sequence begins to have negative values at the 13th term, a13=−13
72) For which terms does the finite arithmetic sequence {52,198,94,...,18} have integer values?
73) Write an arithmetic sequence using a recursive formula. Show the first 4 terms, and then find the 31st term.
- Answer
-
Answers will vary. Check to see that the sequence is arithmetic. Example: Recursive formula: a1=3,an=an−1−3. First 4 terms: 3,0,−3,−6,a31=−87
74) Write an arithmetic sequence using an explicit formula. Show the first 4 terms, and then find the 28th term.
11.3 Geometric Sequences
Verbal
1) What is a geometric sequence?
- Answer
-
A sequence in which the ratio between any two consecutive terms is constant.
2) How is the common ratio of a geometric sequence found?
3) What is the procedure for determining whether a sequence is geometric?
- Answer
-
Divide each term in a sequence by the preceding term. If the resulting quotients are equal, then the sequence is geometric.
4) What is the difference between an arithmetic sequence and a geometric sequence?
5) Describe how exponential functions and geometric sequences are similar. How are they different?
- Answer
-
Both geometric sequences and exponential functions have a constant ratio. However, their domains are not the same. Exponential functions are defined for all real numbers, and geometric sequences are defined only for positive integers. Another difference is that the base of a geometric sequence (the common ratio) can be negative, but the base of an exponential function must be positive.
Algebraic
For the exercises 6-8, find the common ratio for the geometric sequence.
6) 1,3,9,27,81,...
7) −0.125,0.25,−0.5,1,−2,...
- Answer
-
The common ratio is −2
8) −2,−12,−18,−132,−1128,...
For the exercises 9-13, determine whether the sequence is geometric. If so, find the common ratio.
9) −6,−12,−24,−48,−96,...
- Answer
-
The sequence is geometric. The common ratio is 2.
10) 5,5.2,5.4,5.6,5.8,...
11) −1,12,−14,18,−116,...
- Answer
-
The sequence is geometric. The common ratio is −12.
12) 6,8,11,15,20,...
13) 0.8,4,20,100,500,...
- Answer
-
The sequence is geometric. The common ratio is 5.
For the exercises 14-15, write the first five terms of the geometric sequence, given the first term and common ratio.
14) a1=8,r=0.3
15) a1=5,r=15
- Answer
-
5,1,15,125,1125
For the exercises 16-17, write the first five terms of the geometric sequence, given any two terms.
16) a7=64,a10=512
17) a6=25,a8=6.25
- Answer
-
800,400,200,100,50
For the exercises 18-19, find the specified term for the geometric sequence, given the first term and common ratio.
18) The first term is 2, and the common ratio is 3. Find the 5th term.
19) The first term is 16 and the common ratio is −13. Find the 4th term.
- Answer
-
a4=−1627
For the exercises 20-21, find the specified term for the geometric sequence, given the first four terms.
20) an={−1,2,−4,8,...}. Find a12.
21) an={−2,23,−29,227,...}. Find a7.
- Answer
-
a7=−2729
For the exercises 22-23, write the first five terms of the geometric sequence.
22) a1=−486,an=−13an−1
23) a1=7,an=0.2an−1
- Answer
-
7,1.4,0.28,0.056,0.0112
For the exercises 24-31, write a recursive formula for each geometric sequence.
24) an={−1,5,−25,125,...}
25) an={−32,−16,−8,−4,...}
- Answer
-
a1=−32,an=12an−1
26) an={14,56,224,896,...}
27) an={10,−3,0.9,−0.27,...}
- Answer
-
a1=10,an=−0.3an−1
28) an={0.61,1.83,5.49,16.47,...}
29) an={35,110,160,1360,...}
- Answer
-
a1=35,an=126an−1
30) an={−2,43,−89,1627,...}
31) an={1512,−1128,132,−18,...}
- Answer
-
a1=1512,an=−4an−1
For the exercises 32-33, write the first five terms of the geometric sequence.
32) an=−4⋅5n−1
33) an=12⋅(−12)n−1
- Answer
-
12,−2,3,−32,34
For the exercises 34-41, write an explicit formula for each geometric sequence.
34) an={−2,−4,−8,−16,...}
35) an={1,3,9,27,...}
- Answer
-
an=3n−1
36) an={−4,−12,−36,−108,...}
37) an={0.8,−4,20,−100,...}
- Answer
-
an=0.8⋅(−5)n−1
38) an={−1.25,−5,−20,−80,...}
39) an={−1,−45,−1625,−64125,...}
- Answer
-
an=−(45)n−1
40) an={2,13,118,1108,...}
41) an={3,−1,13,−19,...}
- Answer
-
an=3⋅(−13)n−1
For the exercises 42-43, find the specified term for the geometric sequence given.
42) Let a1=4, an=−3an−1. Find a8.
43) Let an=−(−13)n−1. Find a12.
- Answer
-
a12=1177,147
For the exercises 44-45, find the number of terms in the given finite geometric sequence.
44) an={−1,3,−9,...,2187}
45) an={2,1,12,...,11024}
- Answer
-
There are 12 terms in the sequence.
Graphical
For the exercises 46-47, determine whether the graph shown represents a geometric sequence.
46)
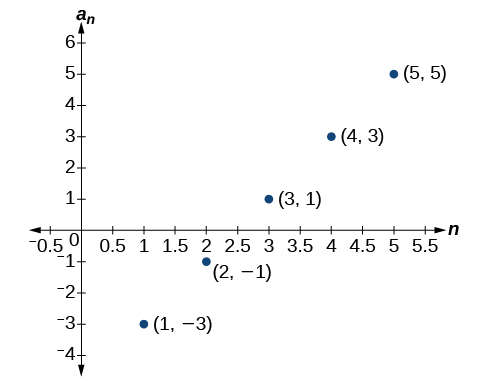
47)
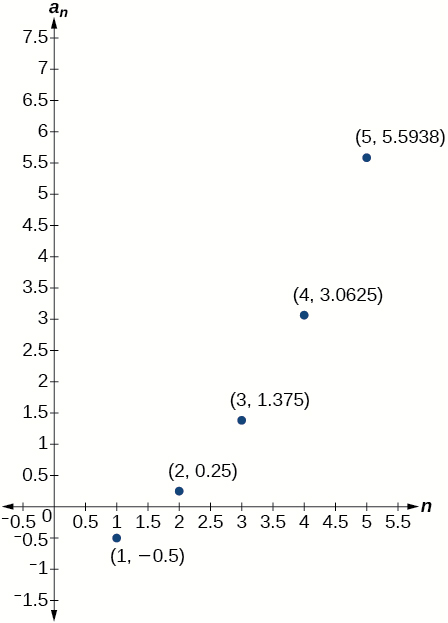
- Answer
-
The graph does not represent a geometric sequence.
For the exercises 48-50, use the information provided to graph the first five terms of the geometric sequence.
48) a1=1,r=12
49) a1=3,an=2an−1
- Answer
-
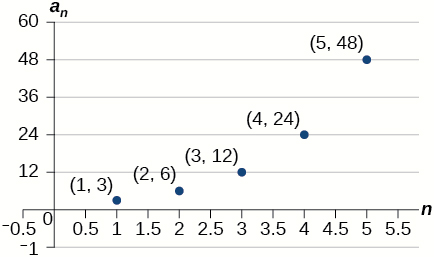
50) an=27⋅0.3n−1
Extensions
51) Use recursive formulas to give two examples of geometric sequences whose 3rd terms are 200.
- Answer
-
Answers will vary. Examples: a1=800,an=0.5an−1 and a1=12.5,an=4an−1
52) Use explicit formulas to give two examples of geometric sequences whose 7th terms are 1024.
53) Find the 5th term of the geometric sequence {b,4b,16b,...}.
- Answer
-
a5=256b
54) Find the 7th term of the geometric sequence {64a(−b),32a(−3b),16a(−9b),...}.
55) At which term does the sequence {10,12,14.4,17.28,...} exceed 100?
- Answer
-
The sequence exceeds 100 at the 14th term, a14≈107.
56) At which term does the sequence {12187,1729,1243,181,...} begin to have integer values?
57) For which term does the geometric sequence an=−36(23)n−1 first have a non-integer value?
- Answer
-
a4=−323
58) Use the recursive formula to write a geometric sequence whose common ratio is an integer. Show the first four terms, and then find the 10th term.
59) Use the explicit formula to write a geometric sequence whose common ratio is a decimal number between 0 and 1. Show the first 4 terms, and then find the 8th term.
- Answer
-
Answers will vary. Example: Explicit formula with a decimal common ratio: an=400⋅0.5n−1; First 4 terms: 400,200,100,50;a8=3.125
60) Is it possible for a sequence to be both arithmetic and geometric? If so, give an example.
11.4 Series and Their Notations
Verbal
1) What is an nth partial sum?
- Answer
-
An nth partial sum is the sum of the first n terms of a sequence.
2) What is the difference between an arithmetic sequence and an arithmetic series?
3) What is a geometric series?
- Answer
-
A geometric series is the sum of the terms in a geometric sequence.
4) How is finding the sum of an infinite geometric series different from finding the nth partial sum?
5) What is an annuity?
- Answer
-
An annuity is a series of regular equal payments that earn a constant compounded interest.
Algebraic
For the exercises 6-9, express each description of a sum using summation notation.
6) The sum of terms m2+3m from m=1 to m=5.
7) The sum from of n=0 to n=4 of 5n
- Answer
-
4∑n=05n
8) The sum of 6k−5 from k=−2 to k−1
9) The sum that results from adding the number 4 five times
- Answer
-
5∑k=14
For the exercises 10-12, express each arithmetic sum using summation notation.
10) 5+10+15+20+25+30+35+40+45+50
11) 10+18+26+…+162
- Answer
-
20∑k=18k+2
12) 12+1+32+2+…+4
For the exercises 13-15, use the formula for the sum of the first n terms of each arithmetic sequence.
13) 32+2+52+3+72
- Answer
-
S5=5(32+72)2
14) 19+25+31+…+73
15) 3.2+3.4+3.6+…+5.6
- Answer
-
S13=13(3.2+5.6)2
For the exercises 16-18, express each geometric sum using summation notation.
16) 1+3+9+27+81+243+729+2187
17) 8+4+2+…+0.125
- Answer
-
7∑k=18⋅0.5k−1
18) −16+112−124+…+1768
For the exercises 19-21, use the formula for the sum of the first n terms of each geometric sequence, and then state the indicated sum.
19) 9+3+1+13+19
- Answer
-
S5=9(1−(13)5)1−13=1219≈13.44
20) 9∑n=15⋅2n−1
21) 11∑a=164⋅0.2a−1
- Answer
-
S11=64(1−0.211)1−0.2=781,249,9849,765,625≈80
For the exercises 22-25, determine whether the infinite series has a sum. If so, write the formula for the sum. If not, state the reason.
22) 12+18+24+30+…
23) 2+1.6+1.28+1.024+…
- Answer
-
The series is defined. S=21−0.8
24) ∞∑m=14m−1
25) ∑k=1∞−(−12)k−1
- Answer
-
The series is defined. S=−11−(−12)
Graphical
For the exercises 26-27, use the following scenario. Javier makes monthly deposits into a savings account. He opened the account with an initial deposit of $50. Each month thereafter he increased the previous deposit amount by $20.
26) Graph the arithmetic sequence showing one year of Javier’s deposits.
27) Graph the arithmetic series showing the monthly sums of one year of Javier’s deposits.
- Answer
-
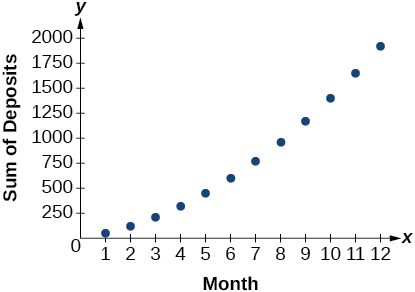
For the exercises 28-29, use the geometric series ∞∑k=1(12)k
28) Graph the first 7 partial sums of the series.
29) What number does Sn seem to be approaching in the graph? Find the sum to explain why this makes sense.
- Answer
-
Sample answer: The graph of Sn seems to be approaching 1. This makes sense because ∞∑k=1(12)k is a defined infinite geometric series with S=121−(12)=1.
Numeric
For the exercises 30-33, find the indicated sum.
30) 14∑a=1a
31) 6∑n=1n(n−2)
- Answer
-
49
32) 17∑k=1k2
33) 7∑k=12k
- Answer
-
254
For the exercises 34-37, use the formula for the sum of the first n terms of an arithmetic series to find the sum.
34) −1.7+−0.4+0.9+2.2+3.5+4.8
35) 6+152+9+212+12+272+15
- Answer
-
S7=1472
36) −1+3+7+…+31
37) 11∑k=1(k2−12)
- Answer
-
S11=552
For the exercises 38-41, use the formula for the sum of the first n terms of a geometric series to find the partial sum.
38) S6 for the series −2−10−50−250…
39) S7 for the series 0.4−2+10−50…
- Answer
-
S7=5208.4
40) 9∑k=12k−1
41) 10∑n=1−2⋅(12)n−1
- Answer
-
S10=−1023256
For the exercises 42-45, find the sum of the infinite geometric series.
42) 4+2+1+12+…
43) −1−14−116−164…
- Answer
-
S=−43
44) ∑k=1∞3⋅(14)k−1
45) ∞∑n=14.6⋅0.5n−1
- Answer
-
S=9.2
For the exercises 46-49, determine the value of the annuity for the indicated monthly deposit amount, the number of deposits, and the interest rate.
46) Deposit amount: $50; total deposits: 60; interest rate: 5%, compounded monthly
47) Deposit amount: $150; total deposits: 24; interest rate: 3%, compounded monthly
- Answer
-
$3705.42
48) Deposit amount: $450; total deposits: 60; interest rate: 4.5%, compounded quarterly
49) Deposit amount: $100; total deposits: 120; interest rate: 10%, compounded semi-annually
- Answer
-
$695,823.97
Extensions
50) The sum of terms 50−k2 from k=x through 7 is 115. What is x?
51) Write an explicit formula for ak such that 6∑k=0ak=189. Assume this is an arithmetic series.
- Answer
-
ak=30−k
52) Find the smallest value of n such that n∑k=1(3k−5)>100.
53) How many terms must be added before the series −1−3−5−7… has a sum less than −75?
- Answer
-
9 terms
54) Write 0.¯65 as an infinite geometric series using summation notation. Then use the formula for finding the sum of an infinite geometric series to convert 0.¯65 to a fraction.
55) The sum of an infinite geometric series is five times the value of the first term. What is the common ratio of the series?
- Answer
-
r=45
56) To get the best loan rates available, the Riches want to save enough money to place 20% down on a $160,000 home. They plan to make monthly deposits of $125 in an investment account that offers 8.5% annual interest compounded semi-annually. Will the Riches have enough for a 20% down payment after five years of saving? How much money will they have saved?
57) Karl has two years to save $10,000 to buy a used car when he graduates. To the nearest dollar, what would his monthly deposits need to be if he invests in an account offering a 4.2% annual interest rate that compounds monthly?
- Answer
-
$400 per month
Real-World Applications
58) Keisha devised a week-long study plan to prepare for finals. On the first day, she plans to study for 1 hour, and each successive day she will increase her study time by 30 minutes. How many hours will Keisha have studied after one week?
59) A boulder rolled down a mountain, traveling 6 feet in the first second. Each successive second, its distance increased by 8 feet. How far did the boulder travel after 10 seconds?
- Answer
-
420 feet
60) A scientist places 50 cells in a petri dish. Every hour, the population increases by 1.5%. What will the cell count be after 1 day?
61) A pendulum travels a distance of 3 feet on its first swing. On each successive swing, it travels 34 the distance of the previous swing. What is the total distance traveled by the pendulum when it stops swinging?
- Answer
-
12 feet
62) Rachael deposits $1,500 into a retirement fund each year. The fund earns 8.2% annual interest, compounded monthly. If she opened her account when she was 19 years old, how much will she have by the time she is 55? How much of that amount will be interest earned?
11.5 Counting Principles
Verbal
For the exercises 1-2, assume that there are n ways an event A can happen, m ways an event B can happen, and that A and B are non-overlapping.
1) Use the Addition Principle of counting to explain how many ways event A or B can occur.
- Answer
-
There are m+n ways for either event A or event B to occur.
2) Use the Multiplication Principle of counting to explain how many ways event A and B can occur.
Answer the questions 3-5.
3) When given two separate events, how do we know whether to apply the Addition Principle or the Multiplication Principle when calculating possible outcomes? What conjunctions may help to determine which operations to use?
- Answer
-
The addition principle is applied when determining the total possible of outcomes of either event occurring. The multiplication principle is applied when determining the total possible outcomes of both events occurring. The word “or” usually implies an addition problem. The word “and” usually implies a multiplication problem.
4) Describe how the permutation of n objects differs from the permutation of choosing r objects from a set of n objects. Include how each is calculated.
5) What is the term for the arrangement that selects r objects from a set of n objects when the order of the r objects is not important? What is the formula for calculating the number of possible outcomes for this type of arrangement?
- Answer
-
A combination; C(n,r)=n!(n−r)!r!
Numeric
For the exercises 6-14, determine whether to use the Addition Principle or the Multiplication Principle. Then perform the calculations.
6) Let the set A={−5,−3,−1,2,3,4,5,6}. How many ways are there to choose a negative or an even number from A?
7) Let the set B={−23,−16,−7,−2,20,36,48,72}. How many ways are there to choose a positive or an odd number from A?
- Answer
-
4+2=6
8) How many ways are there to pick a red ace or a club from a standard card playing deck?
9) How many ways are there to pick a paint color from 5 shades of green, 4 shades of blue, or 7 shades of yellow?
- Answer
-
5+4+7=16
10) How many outcomes are possible from tossing a pair of coins?
11) How many outcomes are possible from tossing a coin and rolling a 6-sided die?
- Answer
-
2×6=12
12) How many two-letter strings—the first letter from A and the second letter from B— can be formed from the sets A={b,c,d} and B={a,e,i,o,u}?
13) How many ways are there to construct a string of 3 digits if numbers can be repeated?
- Answer
-
103=1000
14) How many ways are there to construct a string of 3 digits if numbers cannot be repeated?
For the exercises 15-24, compute the value of the expression.
15) P(5,2)
- Answer
-
P(5,2)=20
16) P(8,4)
17) P(3,3)
- Answer
-
P(3,3)=6
18) P(9,6)
19) P(11,5)
- Answer
-
P(11,5)=55,440
20) C(8,5)
21) C(12,4)
- Answer
-
C(12,4)=495
22) C(26,3)
23) C(7,6)
- Answer
-
C(7,6)=7
24) C(10,3)
For the exercises 25-29, find the number of subsets in each given set.
25) {1,2,3,4,5,6,7,8,9,10}
- Answer
-
210=1024
26) {a,b,c,…,z}
27) A set containing 5 distinct numbers, 4 distinct letters, and 3 distinct symbols
- Answer
-
212=4096
28) The set of even numbers from 2 to 28
29) The set of two-digit numbers between 1 and 100 containing the digit 0
- Answer
-
29=512
For the exercises 30-34, find the distinct number of arrangements.
30) The letters in the word “juggernaut”
31) The letters in the word “academia”
- Answer
-
8!3!=6720
32) The letters in the word “academia” that begin and end in “a”
33) The symbols in the string \#,\#,\#,@,@,\$,\$,\$,\%,\%,\%,\%
- Answer
-
\dfrac{12!}{3!2!3!4!}
34) The symbols in the string \#,\#,\#,@,@,\$,\$,\$,\%,\%,\%,\% that begin and end with “\%”
Extensions
35) The set, S consists of 900,000,000 whole numbers, each being the same number of digits long. How many digits long is a number from S? (Hint: use the fact that a whole number cannot start with the digit 0.)
- Answer
-
9
36) The number of 5-element subsets from a set containing n
37) Can C(n,r) ever equal P(n,r)? Explain.
- Answer
-
Yes, for the trivial cases r=0 and r=1. If r=0, then C(n,r)=P(n,r)=1. If r=1, then r=1, C(n,r)=P(n,r)=n.
38) Suppose a set A has 2,048 subsets. How many distinct objects are contained in A?
39) How many arrangements can be made from the letters of the word “mountains” if all the vowels must form a string?
- Answer
-
\dfrac{6!}{2!}\times 4!=8640
Real-World Applications
40) A family consisting of 2 parents and 3 children is to pose for a picture with 2 family members in the front and 3 in the back.
- How many arrangements are possible with no restrictions?
- How many arrangements are possible if the parents must sit in the front?
- How many arrangements are possible if the parents must be next to each other?
41) A cell phone company offers 6 different voice packages and 8 different data packages. Of those, 3 packages include both voice and data. How many ways are there to choose either voice or data, but not both?
- Answer
-
6-3+8-3=8
42) In horse racing, a “trifecta” occurs when a bettor wins by selecting the first three finishers in the exact order (1^{st} place, 2^{nd} place, and 3^{rd} place). How many different trifectas are possible if there are 14 horses in a race?
43) A wholesale T-shirt company offers sizes small, medium, large, and extra-large in organic or non-organic cotton and colors white, black, gray, blue, and red. How many different T-shirts are there to choose from?
- Answer
-
4\times 2\times 5=40
44) Hector wants to place billboard advertisements throughout the county for his new business. How many ways can Hector choose 15 neighborhoods to advertise in if there are 30 neighborhoods in the county?
45) An art store has 4 brands of paint pens in 12 different colors and 3 types of ink. How many paint pens are there to choose from?
- Answer
-
4\times 12\times 3=144
46) How many ways can a committee of 3 freshmen and 4 juniors be formed from a group of 8 freshmen and 11 juniors?
47) How many ways can a baseball coach arrange the order of 9 batters if there are 15 players on the team?
- Answer
-
P(15,9)=1,816,214,400
48) A conductor needs 5 cellists and 5 violinists to play at a diplomatic event. To do this, he ranks the orchestra’s 10 cellists and 16 violinists in order of musical proficiency. What is the ratio of the total cellist rankings possible to the total violinist rankings possible?
49) A motorcycle shop has 10 choppers, 6 bobbers, and 5 café racers—different types of vintage motorcycles. How many ways can the shop choose 3 choppers, 5 bobbers, and 2 café racers for a weekend showcase?
- Answer
-
C(10,3)\times C(6,5)\times C(5,2)=7,200
50) A skateboard shop stocks 10 types of board decks, 3 types of trucks, and 4 types of wheels. How many different skateboards can be constructed?
51) Just-For-Kicks Sneaker Company offers an online customizing service. How many ways are there to design a custom pair of Just-For-Kicks sneakers if a customer can choose from a basic shoe up to 11 customizable options?
- Answer
-
2^{11}=2048
52) A car wash offers the following optional services to the basic wash: clear coat wax, triple foam polish, undercarriage wash, rust inhibitor, wheel brightener, air freshener, and interior shampoo. How many washes are possible if any number of options can be added to the basic wash?
53) Susan bought 20 plants to arrange along the border of her garden. How many distinct arrangements can she make if the plants are comprised of 6 tulips, 6 roses, and 8 daisies?
- Answer
-
\dfrac{20!}{6!6!8!}=116,396,280
54) How many unique ways can a string of Christmas lights be arranged from 9 red, 10 green, 6 white, and 12 gold color bulbs?
11.6 Binomial Theorem
Verbal
1) What is a binomial coefficient, and how it is calculated?
- Answer
-
A binomial coefficient is an alternative way of denoting the combination C(n,r). It is defined as \dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n-r)!}.
2) What role do binomial coefficients play in a binomial expansion? Are they restricted to any type of number?
3) What is the Binomial Theorem and what is its use?
- Answer
-
The Binomial Theorem is defined as (x+y)^n=\displaystyle \sum_{k=0}^{n}\dbinom{n}{r}x^{n-k}y^k and can be used to expand any binomial.
4) When is it an advantage to use the Binomial Theorem? Explain.
Algebraic
For the exercises 5-12, evaluate the binomial coefficient.
5) \dbinom{6}{2}
- Answer
-
15
6) \dbinom{5}{3}
7) \dbinom{7}{4}
- Answer
-
35
8) \dbinom{9}{7}
9) \dbinom{10}{9}
- Answer
-
10
10) \dbinom{25}{11}
11) \dbinom{17}{6}
- Answer
-
12,376
12) \dbinom{200}{199}
For the exercises 13-22, use the Binomial Theorem to expand each binomial.
13) (4a-b)^3
- Answer
-
64a^3-48a^2b+12ab^2-b^3
14) (5a+2)^3
15) (3a+2b)^3
- Answer
-
27a^3+54a^2b+36ab^2+8b^3
16) (2x+3y)^4
17) (4x+2y)^5
- Answer
-
1024x^5+2560x^4y+2560x^3y^2+1280x^2y^3+320xy^4+32y^5
18) (3x-2y)^4
19) (4x-3y)^5
- Answer
-
1024x^5-3840x^4y+5760x^3y^2-4320x^2y^3+1620xy^4-243y^5
20) \left ( \dfrac{1}{x}+3y \right )^5
21) \left ( x^{-1}+2y^{-1} \right )^4
- Answer
-
\dfrac{1}{x^4}+\dfrac{8}{x^3y}+\dfrac{24}{x^2y^2}+\dfrac{32}{xy^3}+\dfrac{16}{y^4}
22) \left ( \sqrt{x}-\sqrt{y} \right )^5
For the exercises 23-29, use the Binomial Theorem to write the first three terms of each binomial.
23) (a+b)^{17}
- Answer
-
a^{17}+17a^{16}b+136a^{15}b^2
24) (x-1)^{18}
25) (a-2b)^{15}
- Answer
-
a^{15}-30a^{14}b+420a^{13}b^2
26) (x-2y)^8
27) (3a+b)^{20}
- Answer
-
3,486,784,401a^{20}+23,245,229,340a^{19}b+73,609,892,910a^{18}b^2
28) (2a+4b)^7
29) \left ( x^3-\sqrt{y} \right )^8
- Answer
-
x^{24}-8x^{21}\sqrt{y}+28x^{18}y
For the exercises 30-39, find the indicated term of each binomial without fully expanding the binomial.
30) The fourth term of (2x-3y)^4
31) The fourth term of (3x-2y)^5
- Answer
-
-720x^2y^3
32) The third term of (6x-3y)^7
33) The eighth term of (7+5y)^{14}
- Answer
-
220,812,466,875,000y^7
34) The seventh term of (a+b)^{11}
35) The fifth term of (x-y)^{7}
- Answer
-
35x^3y^4
36) The tenth term of (x-1)^{12}
37) The ninth term of (a-3b^2)^{11}
- Answer
-
1,082,565a^3b^{16}
38) The fourth term of \left ( x^3-\dfrac{1}{2} \right )^{10}
39) The eighth term of \left ( \dfrac{y}{2}+\dfrac{2}{x} \right )^{9}
- Answer
-
\dfrac{1152y^2}{x^7}
Graphical
For the exercises 40-44, use the Binomial Theorem to expand the binomial f(x)=(x+3)^4. Then find and graph each indicated sum on one set of axes.
40) Find and graph f_1(x), such that f_1(x) is the first term of the expansion.
41) Find and graph f_2(x), such that f_2(x) is the sum of the first two terms of the expansion.
- Answer
-
f_2(x)=x^4+12x^3
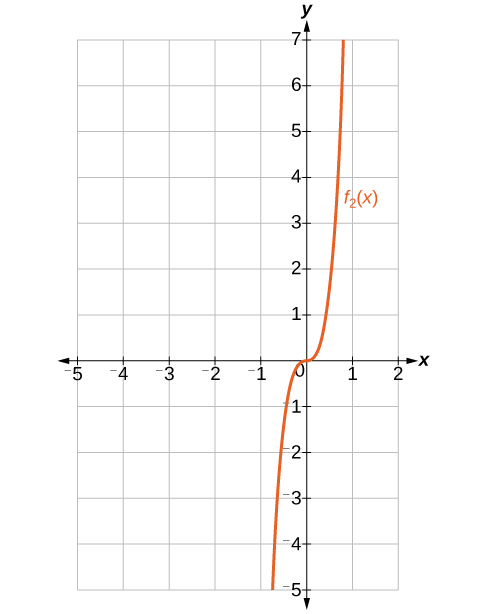
42) Find and graph f_3(x), such that f_3(x) is the sum of the first three terms of the expansion.
43) Find and graph f_4(x), such that f_4(x) is the sum of the first four terms of the expansion.
- Answer
-
f_4(x)=x^4+12x^3+54x^2+108x
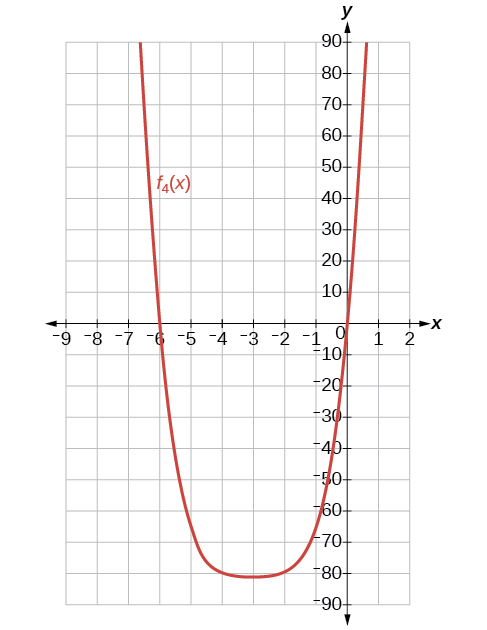
44) Find and graph f_5(x), such that f_5(x) is the sum of the first five terms of the expansion.
Extensions
45) In the expansion of (5x+3y)^n, each term has the form \dbinom{n}{k}a^{n-k}b^k where k successively takes on the value 0,1,2,\ldots ,n. If \dbinom{n}{k}=\dbinom{7}{2}, what is the corresponding term?
- Answer
-
590,625x^5y^2
46) In the expansion of (a+b)^n, the coefficient of a^{n-k}b^k is the same as the coefficient of which other term?
47) Consider the expansion of (x+b)^{40}. What is the exponent of b in the k\text {th} term?
- Answer
-
k-1
48) Find \dbinom{n}{k-1}+\dbinom{n}{k} and write the answer as a binomial coefficient in the form \dbinom{n}{k}. Prove it. Hint: Use the fact that, for any integer p, such that p\geq 1, p!=p(p-1)!.
- Answer
-
\begin{align*} \dbinom{n}{k-1}+\dbinom{n}{k} &= \dfrac{n!}{k!(n-k)!}+\frac{n!}{(k-1)!(n-(k-1))!}\\ &= \dfrac{n!}{k!(n-k)!}+\frac{n!}{(k-1)!(n-k+1)!}\\ &= \dfrac{(n-k+1)n!}{(n-k+1)k!(n-k)!}+\frac{kn!}{k(k-1)!(n-k+1)!}\\ &= \dfrac{(n-k+1)n!+kn!}{k!(n-k+1)!}\\ &= \dfrac{(n+1)n!}{k!((n+1)-k)!}\\ &= \dfrac{(n+1)!}{k!((n+1)-k)!}\\ &= \dbinom{n+1}{k} \end{align*}
49) Which expression cannot be expanded using the Binomial Theorem? Explain.
- (x^2-2x+1)
- \left ( \sqrt{a}+4\sqrt{a}-5 \right )^8
- (x^3+2y^2-z)^5
- \left ( 3x^2-\sqrt{2y^3} \right )^{12}
- Answer
-
The expression (x^3+2y^2-z)^5 cannot be expanded using the Binomial Theorem because it cannot be rewritten as a binomial.
11.7 Probability
Verbal
1) What term is used to express the likelihood of an event occurring? Are there restrictions on its values? If so, what are they? If not, explain.
- Answer
-
probability; The probability of an event is restricted to values between 0 and 1, inclusive of 0 and 1.
2) What is a sample space?
3) What is an experiment?
- Answer
-
An experiment is an activity with an observable result.
4) What is the difference between events and outcomes? Give an example of both using the sample space of tossing a coin 50 times.
5) The union of two sets is defined as a set of elements that are present in at least one of the sets. How is this similar to the definition used for the union of two events from a probability model? How is it different?
- Answer
-
The probability of the union of two events occurring is a number that describes the likelihood that at least one of the events from a probability model occurs. In both a union of sets A and B and a union of events A and B, the union includes either A or B or both. The difference is that a union of sets results in another set, while the union of events is a probability, so it is always a numerical value between 0 and 1.
Numeric
For the exercises 6-13, use the spinner shown in the Figure below to find the probabilities indicated.
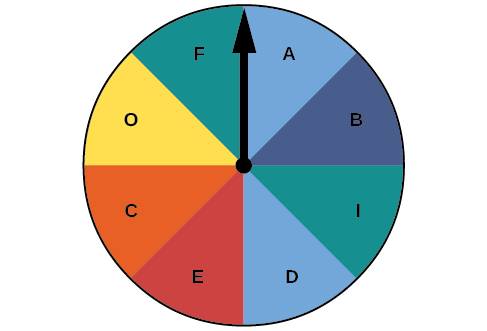
6) Landing on red
7) Landing on a vowel
- Answer
-
\dfrac{1}{2}
8) Not landing on blue
9) Landing on purple or a vowel
- Answer
-
\dfrac{5}{8}
10) Landing on blue or a vowel
11) Landing on green or blue
- Answer
-
\dfrac{1}{2}
12) Landing on yellow or a consonant
13) Not landing on yellow or a consonant
- Answer
-
\dfrac{3}{8}
For the exercises 14-17, two coins are tossed.
14) What is the sample space?
15) Find the probability of tossing two heads.
- Answer
-
\dfrac{1}{4}
16) Find the probability of tossing exactly one tail.
17) Find the probability of tossing at least one tail.
- Answer
-
\dfrac{3}{4}
For the exercises 18-25, four coins are tossed.
18) What is the sample space?
19) Find the probability of tossing exactly two heads.
- Answer
-
\dfrac{3}{8}
20) Find the probability of tossing exactly three heads.
21) Find the probability of tossing four heads or four tails.
- Answer
-
\dfrac{1}{8}
22) Find the probability of tossing all tails.
23) Find the probability of tossing not all tails.
- Answer
-
\dfrac{15}{16}
24) Find the probability of tossing exactly two heads or at least two tails.
25) Find the probability of tossing either two heads or three heads.
- Answer
-
\dfrac{5}{8}
For the exercises 26-32, one card is drawn from a standard deck of 52 cards. Find the probability of drawing the following:
26) A club
27) A two
- Answer
-
\dfrac{1}{13}
28) Six or seven
29) Red six
- Answer
-
\dfrac{1}{26}
30) An ace or a diamond
31) A non-ace
- Answer
-
\dfrac{12}{13}
32) A heart or a non-jack
For the exercises 33-42, two dice are rolled, and the results are summed.
33) Construct a table showing the sample space of outcomes and sums.
- Answer
-
1 2 3 4 5 6 1 (1, 1)
2(1, 2)
3(1, 3)
4(1, 4)
5(1, 5)
6(1, 6)
72 (2, 1)
3(2, 2)
4(2, 3)
5(2, 4)
6(2, 5)
7(2, 6)
83 (3, 1)
4(3, 2)
5(3, 3)
6(3, 4)
7(3, 5)
8(3, 6)
94 (4, 1)
5(4, 2)
6(4, 3)
7(4, 4)
8(4, 5)
9(4, 6)
105 (5, 1)
6(5, 2)
7(5, 3)
8(5, 4)
9(5, 5)
10(5, 6)
116 (6, 1)
7(6, 2)
8(6, 3)
9(6, 4)
10(6, 5)
11(6, 6)
12
34) Find the probability of rolling a sum of 3.
35) Find the probability of rolling at least one four or a sum of 8.
- Answer
-
\dfrac{5}{12}
36) Find the probability of rolling an odd sum less than 9.
37) Find the probability of rolling a sum greater than or equal to 15.
- Answer
-
0
38) Find the probability of rolling a sum less than 15.
39) Find the probability of rolling a sum less than 6 or greater than 9.
- Answer
-
\dfrac{4}{9}
40) Find the probability of rolling a sum between 6 and 9, inclusive.
41) Find the probability of rolling a sum of 5 or 6.
- Answer
-
\dfrac{1}{4}
42) Find the probability of rolling any sum other than 5 or 6.
For the exercises 43-46, a coin is tossed, and a card is pulled from a standard deck. Find the probability of the following:
43) A head on the coin or a club
- Answer
-
\dfrac{5}{8}
44) A tail on the coin or red ace
45) A head on the coin or a face card
- Answer
-
\dfrac{8}{13}
46) No aces
For the exercises 47-50, use this scenario: a bag of M&Ms contains 12 blue, 6 brown, 10 orange, 8 yellow, 8 red, and 4 green M&Ms. Reaching into the bag, a person grabs 5 M&Ms.
47) What is the probability of getting all blue M&Ms?
- Answer
-
\dfrac{C(12,5)}{C(48,5)}=\dfrac{1}{2162}
48) What is the probability of getting 4 blue M&Ms?
49) What is the probability of getting 3 blue M&Ms?
- Answer
-
\dfrac{C(12,3)C(36,2)}{C(48,5)}=\dfrac{175}{2162}
50) What is the probability of getting no brown M&Ms?
Extensions
Use the following scenario for the exercises that follow: In the game of Keno, a player starts by selecting 20 numbers from the numbers 1 to 80. After the player makes his selections, 20 winning numbers are randomly selected from numbers 1 to 80. A win occurs if the player has correctly selected 3,4 or 5 of the 20 winning numbers. (Round all answers to the nearest hundredth of a percent.)
51) What is the percent chance that a player selects exactly 3 winning numbers?
- Answer
-
\dfrac{C(20,3)C(60,17)}{C(80,20)}\approx 12.49\%
52) What is the percent chance that a player selects exactly 4 winning numbers?
53) What is the percent chance that a player selects all 5 winning numbers?
- Answer
-
\dfrac{C(20,5)C(60,15)}{C(80,20)}\approx 23.33\%
54) What is the percent chance of winning?
55) How much less is a player’s chance of selecting 3 winning numbers than the chance of selecting either 4 or 5 winning numbers?
- Answer
-
20.50+23.33-12.49=31.34\%
Real-World Applications
Use this data for the exercises 56-60: In 2013, there were roughly 317 million citizens in the United States, and about 40 million were elderly (aged 65 and over)
56) If you meet a U.S. citizen, what is the percent chance that the person is elderly? (Round to the nearest tenth of a percent.)
57) If you meet five U.S. citizens, what is the percent chance that exactly one is elderly? (Round to the nearest tenth of a percent.)
- Answer
-
\dfrac{C(40000000,1)C(277000000,4)}{C(317000000,5)}\approx 36.78\%
58) If you meet five U.S. citizens, what is the percent chance that three are elderly? (Round to the nearest tenth of a percent.)
59) If you meet five U.S. citizens, what is the percent chance that four are elderly? (Round to the nearest thousandth of a percent.)
- Answer
-
\dfrac{C(40000000,4)C(277000000,1)}{C(317000000,5)}\approx 0.11\%
60) It is predicted that by 2030, one in five U.S. citizens will be elderly. How much greater will the chances of meeting an elderly person be at that time? What policy changes do you foresee if these statistics hold true?
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


