6.3: Official Definition

The preceding section provided some intuition about how and why functions are represented as sets of ordered pairs, but it is not at all authoritative. Here are the official definitions.

Definition \(6.3.1\).

Suppose \(A\) and \(B\) are sets.

1. A set \(f\) is a function from \(A\) to \(B\) iff
   1. each element of \(f\) is an ordered pair \((a, b)\), such that \(a \in A\) and \(b \in B\), and
   2. for each \(a \in A\), there is a unique \(b \in B\), such that \((a, b) \in f\).
2. If \(f\) is a function from \(A\) to \(B\), then
   • \(A\) is called the domain of \(f\), and
   • \(B\) is a codomain of \(f\).
3. We write “\(f : A \rightarrow B\)” to denote that \(f\) is a function from \(A\) to \(B\).

Exercise \(6.3.2\).

We can express the definition of a function in First-Order Logic:

1. Translate the assertion of Definition \(6.3.1(1a)\) into First-Order Logic.
2. Translate the assertion of Definition \(6.3.1(1b)\) into First-Order Logic.

Notation \(6.3.3\).

Suppose \(f: A \rightarrow B\).

1. For \(a \in A\), it is convenient to have a name for the element \(b\) of \(B\), such that \((a, b) \in f\). The name we use is \(f(a)\): \[f(a)=b \text { if and only if }(a, b) \in f \text {. }\]
2. Each element \(a\) of \(A\) provides us with an element \(f(a)\) of \(B\). The range of \(f\) is the set that collects together all of these elements \(f(a)\). That is, \[b \text { is in the range of } f \text { iff there is some } a \in A, \text { such that } b=f(a) \text {. }\]
   The range can be denoted \(\{f(a) \mid a \in A\}\).

Example \(6.3.4\).

Suppose the function \(f\) is defined by \(f(x) = x^{2}\), on the domain \(\{0,1,2,4\}\). Then:

1. To represent \(f\) as a set of ordered pairs, each element of the domain must appear exactly once as a first coordinate, with the corresponding output given in the second coordinate. Since there are four elements in the domain, there will be four ordered pairs: \(f=\{(0,0),(1,1),(2,4),(4,16)\}\).
2. To give a table for \(f\), we include one row for every element of the domain. The table will be:

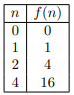
3. If we are asked what is \(f(3)\), the answer is that \(f(3)\) does not exist, because 3 is not in the domain of \(f\). Even though we know that \(3^{2} = 9\), the formula we gave for \(f\) only applies to elements that are in the domain of \(f!\) It is not true that \(f(3) = 9\).
4. The range of \(f\) is the set of possible outputs: in this case, the range of \(f\) is \(\{0, 1, 4, 16\}\).
5. If we are asked what is \(f(2)\), the answer is \(f(2) = 4\).
6. Is \(f\) a function from \(\{n \in \mathbb{N} \mid n \leq 4\}\) to \(\{0, 1, 4, 16\}\)? The answer is no, because the first set is \(\{0, 1, 2, 3, 4\}\), which includes the value 3, but 3 is not in the domain of \(f\).
7. Is \(f\) a function from \(\{0, 1, 2, 4\}\) to \(\{n \in \mathbb{N} \mid n \leq 16\}\)? The answer is yes; even though the second set has many values that are not in the range, it is a possible codomain for \(f\). A codomain can be any set that contains all of the elements of the range, so every function has many different codomains (but only one domain and only one range).

Exercise \(6.3.5\).

1. The table at right describes a certain function \(g\).
   
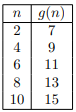
   1. What is the domain of \(g\)?
   2. What is the range of \(g\)?
   3. What is \(g(6)\)?
   4. What is \(g(7)\)?
   5. Represent \(g\) as a set of ordered pairs.
   6. Draw an arrow diagram to represent \(g\).
   7. Write down a formula that describes \(g\).
      (Express \(g(n)\) in terms of \(n\), by using simple arithmetic operations.)
2. Suppose
   • \(f\) is a function whose domain is \(\{0, 2, 4, 6\}\), and
   • \(f(x) = 4x − 5\), for every \(x\) in the domain.
     Describe the function in each of the following ways:
     1. Make a table.
     2. Draw an arrow diagram.
     3. Use ordered pairs.
3. For the given sets \(A\) and \(B\):
   1. Write each function from \(A\) to \(B\) as a set of ordered pairs.
   2. Write down the range of each function.
      1. \(A = \{a, b, c\}, B = \{d\}\)
      2. \(A = \{a, b\}, B = \{c, d\}\)
      3. \(A = \{a\}, B = \{b, c, d\}\)
      4. \(A = \{a, b\}, B = \{c, d, e\}\)
         [Hint: For (i), you may assume, without proof, that if \(A\) has exactly \(m\) elements, and \(B\) has exactly \(n\) elements, then the number of functions from \(A\) to \(B\) is \(n^{m}\). (Do you see why this is the correct number?)]
4. Which of the following sets of ordered pairs are functions from \(\{x, y, z\}\) to \(\{a, b, c, d, e\}\)?
   • If it is such a function, then what is its range?
   • If it is not such a function, then explain why not.
     1. \(\{(y, a),(x, b),(y, c)\}\)
     2. \(\{(y, a),(x, b),(z, c)\}\)
     3. \(\{(y, a),(x, c),(z, a)\}\)

Example \(6.3.6\).

If \(A\) is a set, then any function from \(A \times A\) to \(A\) is called a binary operation on \(A\). However, when \(+\) is a binary operation and \(a, b \in A\), we write \(a + b\) for the value of the function at \((a, b)\), instead of writing \(+((a, b))\). See Section \(5.2\) for some examples and many exercises about binary operations.