6.5: Onto functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
In an arrow diagram of a function f:A→B, the definition of a function requires that there is exactly one arrow out of each element of A, but it says nothing about the number of arrows into each element of B. There may be elements of B with lots of arrows into them (unless the function is one-to-one), and there may be other elements of B that have no arrows into them. The function is called “onto” if all of the elements of B are hit by arrows; none are missed.
Figure 6B shows arrow diagrams of various functions, some onto and some not.
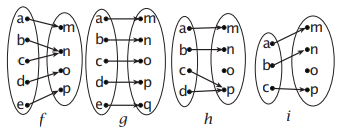
Not every woman is a mother. This means that if you draw an arrow from each person to his or her mother, there will be some women who have no arrows into them. So the function mother: People → Women
is not onto.
The following official definition of “onto” formalizes the ideas described above.
Suppose f:A→B. We say f is onto iff, for all b∈B, there is some a∈A, such that f(a)=b.
Suppose f:A→B and g:X→Y. Translate each of the following assertions into First-Order Logic:
- f is onto.
- f is not onto.
- g is onto.
- g is not onto.
(Simplify your answers in (3) and (4) so that ¬ is applied only to predicates.)
Without giving formal proofs, let us demonstrate that each of the following functions is not onto.
- f:R→R, defined by f(x)=|x|.
- g:{1,2,3}→{a,b,c} defined by g={(1,b),(2,a),(3,a)}.
Solution
- Recall that the absolute value of a real number can never be negative. In particular, we can never have |x|=−1 for any real number x. Thus, there does not exist x∈R, such that f(x)=−1. This shows that f is not onto.
- Notice that c never appears as the second coordinate of an ordered pair in this function. This means there does not exist any x, such that g(x)=c. This means that g is not onto.
Each of the following sets of ordered pairs is a function from {1,2,3,4,5} to {♣, ♦, ♥, ♠}. Which of the functions are onto? Briefly justify your answers.
- a= {(1, ♣),(2, ♦),(3, ♥),(4, ♠),(5, ♣)}
- b= {(1, ♣),(2, ♥),(3, ♣),(4, ♥),(5, ♣)}
- c= {(1, ♥),(2, ♥),(3, ♥),(4, ♥),(5, ♥)}
- d= {(1, ♦),(2, ♠),(3, ♥),(4, ♠),(5, ♣)}
- e= {(1, ♣),(2, ♠),(3, ♥),(4, ♠),(5, ♣)}
Let us see how to prove that a function f:A→B is onto. By definition, we wish to show: for all b∈B, there is some a∈A, such that f(a)=b.
In other words: “∀b∈B,∃a∈A,(f(a)=b).”
The first quantifier is ∀; we are required to prove something about every element of B. Hence, we use ∀-introduction, so our proof should start with the sentence “Let b be an arbitrary element of B.” (However, this can be abbreviated to: “Given b∈B,…”) After this, our task will be to prove “∃a∈A,(f(a)=b).”
At this point, the quantifier that concerns us is ∃; we are required to prove that some element of A has a certain property. The tool to use for this is ∃-introduction: we find (or “construct”) an appropriate element of A, and then verify that it does what it is supposed to. Thus, the next step in the proof is “Let a=???” (where ??? needs to be replaced with an appropriate expression). Then all that remains is to verify that the value we assigned to a does the job it is required to do: calculate that f(a) is indeed equal to b.
So here what a typical “onto” proof looks like: Given b∈B, let a=◻ Then f(a)=⋯=b.
An appropriate value for a needs to be put in the box (perhaps a formula that depends on b), and the dots need to be filled in with a calculation that shows the value of f(a) is b. (Also, of course, some of the letters will need to be changed if the name of the function is not f, or if the sets are not called A and B.)
Define g:R→R by g(x)=5x−2. Show g is onto.
Scratchwork. We wish to show ∀y∈R,∃x∈R, (g(x)=y). By ∀-introduction, the first words of the proof are easy: “Given y∈R.” Then we need to find a value of x that makes g(x)=y. The appropriate value of x is probably not obvious, so we will do some scratchwork. We postulate the desired equation g(x)=y and use algebra to solve it: g(x)=y5x−2=y5x=y+2x=y+25.
Now that we know the correct value of x, it is easy to write the rest of the proof.
Solution
Given y∈R, let x=(y+2)/5∈R. Then g(x)=5x−2=5(y+25)−2=(y+2)−2=y.
Each formula defines a function from R to R. Show the function is onto.
- f(x)=2x+1.
- g(x)=7x−3.
- h(t)=4t+9.
- i(z)=6−11z.
- j(r)=(3r−4)/5.
Some “onto” proofs are more complicated than what is described above, because it may not be possible to go directly from “given b∈B” to “let a=◻.” The problem is that it is sometimes necessary to insert calculations (or other explanations) between “given b” and “let a.” Some examples of this will be seen in Exercise 6.8.14.
To complete the discussion, let us also see how to prove that a function f:A→B is not onto. By negating the definition of “onto,” we see that we wish to prove “∃b∈B,∀a∈A,(f(a)≠b).”
The first quantifier is ∃; we are required to prove that some element of B has a certain property. The tool to use for this is ∃-introduction: we find an appropriate element of B, and then we will need to verify that it does what it is supposed to. Thus, the first step in the proof is “Let b=???” (where ??? needs to be replaced with an appropriate expression). After this, our task will be to prove “∀a∈A,(f(a)≠b).”
At this point, the quantifier that concerns us is ∀; we are required to prove something about every element of A. Hence, we use ∀-introduction, so the next step in our proof is the sentence “Let a be an arbitrary element of A” (or, for short,“Given a∈A,…”). Then all that remains is to verify that f(a)≠b.
So here what a typical “not onto” proof looks like: Let b=◻∈B. Given a∈A, we have ..., so f(a)≠b.
An appropriate value for b needs to be put in the box, and the dots need to be filled in with an explanation that leads to the conclusion f(a)≠b. (Also, as usual, some of the letters will need to be changed if the name of the function is not f, or if the sets are not called A and B.)
Define e:R→R by e(r)=1/(|r|+1). Show e is not onto.
Scratchwork. We wish to prove ∃y∈R,∀r∈R,(e(r)≠y), so we need to come up with an appropriate value of y. To do this, let’s attempt to prove e is onto. Hopefully, we will run into trouble, and this difficulty will point us to a good choice for y. Namely, if e were onto, we would be able to solve the equation e(r)=y
Let’s put in the definition of e(r), and use algebra to try to solve this equation: 1|r|+1=y|r|+1=1y|r|=1y−1
Now the absolute value |r| is never negative, but the right-hand side of the equation could be negative. For example, if y=−1, then 1−1−1=−1−1=−2<0.
This suggests that we should let y=−1. With this in mind, we can write the proof.
Solution
PROOF.
Let y=−1. Given r∈R, we have |r|≥0, so |r|+1≥0+1=1>0. Therefore e(r)=1|r|+1≥0>−1=y,
so e(r)≠y. Since r is an arbitrary element of the domain R, this implies that e is not onto.
And sometimes you will need to decide whether a function is onto or not.
Define m:R×R→R by m(x,y)=x+y. Is m onto?
Scratchwork. Let’s try to prove m is onto. (If we fail, this is evidence that m is not onto, and we will try to prove that.) Given z∈R, we try to solve the equation m(x,y)=z.
In other words: x+y=z.
It is easy to find values of x and y that satisfy the equation: perhaps the easiest solution is to let y=0 and x=z. We can use these values to prove that m is onto.
Solution
m is onto.
PROOF. Given z∈R, let (x,y)=(z,0)∈R×R. Then m(x,y)=x+y=z+0=z.
Each formula defines a function from R to R. Which of the functions are onto? Prove that your answers are correct.
- f(x)=1.
- a(x)=x.
- b(t)=t2.
- c(s)=3s+2.
- d(r)=3√r+5−5.
Suppose f:A→B. Show that f is onto if and only if the range of f is B.
(alternative terminology). Some mathematicians say “surjective,” rather than “onto.” (Like “injective” in place of “one-to-one,” this comes from French.) Also, a function that is onto can be called a surjection.


